| Скачать .docx | Скачать .pdf |
Курсовая работа: Моделирование и определение основных свойств волны Лява
Кафедра общей и прикладной геофизики
Курсовая работа по сейсморазведке на тему:
Моделирование и определение основных свойств волны Лява
Выполнили: студенты 3-го курса
Блинов И.В.
Медведева В.А.
Ионов А.М.
Проверил:
Доц. Сердобольский Л.А.
Дубна, 2005
Оглавление
Теоретическое обоснование волн Лява
Введение
В однородной безграничной среде, как следует из физико-геологических основ сейсморазведки, может существовать три типа объёмных сейсмических волн: одна продольная P и две поперечные - SH и SV. При появлении в среде сейсмических границ любая из этих волн в результате явлений отражения и преломления порождает класс вторичных объёмных волн - отражённых и преломленных (головных) сейсмических волн. Существование свободной сейсмической границы L0 - поверхности полупространства, контактирующего с вакуумом (или воздушной средой), обуславливает появление ещё одного, особого, класса волн - поверхностных сейсмических волн.
Упругие волны, возбуждаемые упругим сейсмическим источником, находящимся на поверхности однородного упругого изотропного полупространства с упругими модулями λ, μ, ρ, впервые изучены Лэмбом. Из полученных им результатов вытекает, что в такой среде появляются поверхностные волны. Поверхностная волна Лява одна из таких волн.
В сейсморазведке исследуемые в работе волны играют обычно роль помех. Поэтому знание их свойств необходимо для борьбы с ними. При решении задач инженерной сейсморазведки поверхностные волны служат достаточно надёжным источником сведений о характере распределения скорости распространения поперечных волн в верхней части разреза.
При ведении сейсмических работ на поперечных SH волнах в слоистом (неоднородном по вертикали) полупространстве возбуждаются поперечные поверхностные волны, которые принято называть волнами Лява.
Для этих волн характерна зависимость фазовой скорости распространения от частоты регистрации. Это явление принято называть частотной дисперсией.
Теоретическое обоснование волн Лява
Рассмотрим среду, состоящую из однородного полупространства, перекрытого однородным слоем мощности h. Кровля этого слоя является свободной границей. Сделаем естественное предположение, что скорость распространения поперечных волн в слое VS 1 меньше скорости распространения поперечных волн VS 2 в полупространстве. Предположим, что в таких условиях проводятся сейсмические работы с использованием поперечных волн типа SН. В этом случае наряду с объемными волнами SН могут существовать родственные им поверхностные волны типа Лява. Начало декартовой системы координат поместим на дневной поверхности. Ось 0Z направим вертикально вниз, ось ОХ - по направлению распространения сейсмических волн. В соответствии с предположением о структуре сейсмических волн вектор смещения в искомой волне должен иметь вид в слое:
(1)
в полупространстве:
, (2)
где ω - круговая частота; VL - скорость распространения искомой волны Лява. U и W компоненты вектора смещения, которые вводятся следующим образом:
и 
Как было показано ранее, вектор смещения и все его компоненты должны удовлетворять волновому уравнению вида:
. (3)
Подставляя в это уравнение соответственно компоненты V1 (х, z, t) и V2 (х, у,t), получим, что искомые функции А (z) и В (z) должны являться решением следующих дифференциальных уравнений:
; 
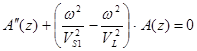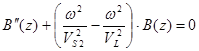; (4)
Из очевидных физических соображений следует допустить, что искомая скорость распространения волн Лява должна быть заключена в интервале
. (5)
При этих предположениях в качестве решений, обеспечивающих убывание амплитуды колебаний в волне Лява в бесконечности (по оси OZ), следует взять:
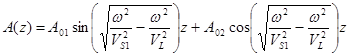; (6)
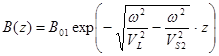, (7)
где А01 , А02 , В01 - константы интегрирования.
Граничные условия на свободной поверхности требуют обращения в нуль всех компонент нормального вектора напряжения Рz . В силу сделанного предположения о структуре компонент вектора смещения, это условие эквивалентно следующему:
. (8)
На границе слоя и полупространства должна выполняться непрерывность компонент вектора напряжения и вектора смещения. Эти условия, как легко видеть, трансформируются в следующие два уравнения:
; (9)
. (10)
С учетом (5) компоненты смещения могут быть представлены в виде:
; (11)
, (12)
где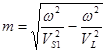 
; 
.
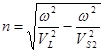Подставляя выражение для смещения в первом слое в граничное условие (8), получим: А01 = 0. С учетом этого результата из условия (9) легко получить уравнение
. (13)
Выполнив третье краевое условие (10), получим уравнение
. (14)
Рассматривая (13) и (14) как систему двух линейных уравнений относительно двух неизвестных А02 и B01 , можно сделать заключение, что нетривиальное решение этой системы будет возможно только в случае равенства нулю ее главного определителя
. (15)
Это уравнение целесообразно представить в виде:
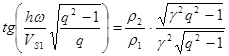, (16)
где 
; 
.
Если это уравнение записать в другом виде и учесть многозначность функции arctg, то основное характеристическое уравнение (16) решаемой задачи можно представить в виде:
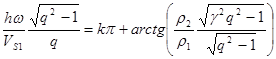, (17)
где k - целое число, определяющее порядок (номер) гармоники волны Лява. Значение k = 0 соответствует первой, основной гармонике волн Лява. Полученное характеристическое уравнение является трансцендентным. Оно определяет бесчисленное множество зависимостей (VL (ω)) k искомой скорости волн Лява от параметров разреза и частоты.
Найденная скорость волны Лява носит название фазовой скорости и ее величина, помимо прочего, зависит от частоты колебаний и номера гармоники k - номера корня уравнения (17). Это означает, что в изучаемом разрезе может наблюдаться целая серия гармоник волн Лява. В реальных условиях в зависимости от параметров разреза и частоты обычно могут наблюдаться две или более гармоник (рис.1).
Из уравнения (17) следует, что при неограниченном увеличении частоты (ω → ∞) фазовая скорость любой гармоники волн Лява асимптотически приближается к скорости распространения поперечных волн в слое. Наоборот, при неограниченном уменьшении частоты (ω → 0) фазовые скорости всех гармоник приближаются к значению скорости распространения поперечных волн в полупространстве (рис).
Перепишем уравнение (17) в следующем виде
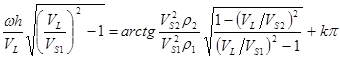, (18)
Воспользуемся тем, что
(18а)
тогда подставляя (18а) в (18), получим
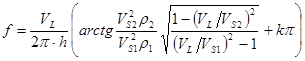. (19)
Рассмотрим предельные случаи:
Когда VL
= V1
и ω → ∞, то 
, очевидно λ → 0.
Когда VL = V2 и ω → ∞, то λ → ∞.
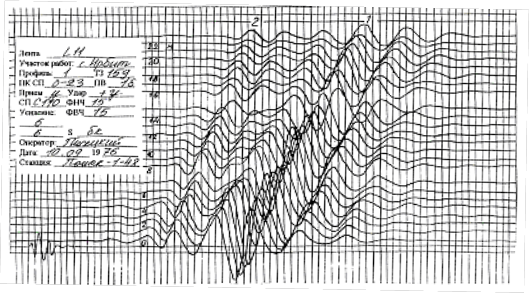
Рис.1. Запись гармоник поверхностных волн Лява: 1 - первая гармоника; 2 - вторая гармоника
Найдя корни характеристического уравнения (17) - численную зависимость фазовой скорости от частоты для конкретной гармоники k - компоненты векторов смещения в слое и полупространстве можно рассчитать по формулам:
; (18)
. (19)
Полученные формулы описывают все кинематические и динамические особенности распространения гармоник волн Лява в рассмотренной модели среды.
Расчётная часть
Теперь рассмотрим зависимость скорости волны Лява от частоты (рис.2). Здесь мы взяли следующие константы, характеризующие систему, состоящую из двух слоёв, плотностями ρ1 = 2,2 г/см3 , ρ2 = 2,4 г/см3 , считаем, что скорость волны в первом слое V1 = 800 м/с, а во втором - V2 = 1400 м/с. Мощность перекрывающего слоя h = 10 м. На графике изображены зависимости при различных k = 0, 1,2. Очевидно, что график 1 соответствует случаю k = 0. Заметим, что все кривые стремятся к значению VL = V1 , тогда частота f стремится к бесконечности. Верхней асимптотой служит значение скорости в полупространстве. Стоит отметить, что график 1 для основной моды фазовой скорости волны Лява, а остальные - это высших гармоник.
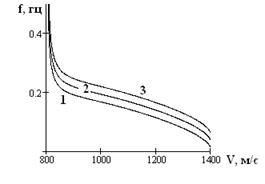
Рис.2. Зависимость частоты волны от её скорости.
Рассмотрим теперь зависимость длины волны λ от скорости волны VL . Используя формулу
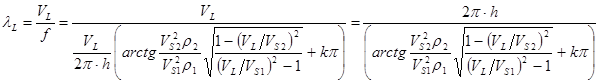
Получим для тех же значений плотности, скорости и мощности h соответствующий график (рис.3).
Здесь видно, что при k = 0 мы получаем график 1, соответственно при k = 2 получим график 3. Смысл состоит в том, что при равенстве скорости волны Лява скорости в первом слое, длина волны при этом стремится к 0. И, наоборот, если скорость волны Лява приближается к скорости во втором слое, то длина волны стремится к бесконечности.
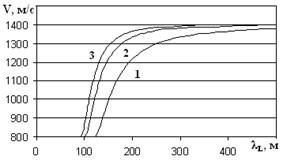
Рис.3. Зависимость длины волны от её скорости.
Тем самым, мы показали, что скорость волны целиком и полностью зависит от параметров разреза и частоты.
Список литературы
1. Бондарев В.И., 2000, Основы сейсморазведки. Екатеринбург: Изд-во УГГГА.
2. Сейсморазведка: Справочник геофизика, 1990/ Под ред.В.П. Номоконова. М.: Недра.
3. Гурвич И.И., Боганик Г.Н., 1980, Сейсморазведка. М.: Недра.