| Скачать .docx | Скачать .pdf |
Реферат: Элементы геодезических разбивочных работ
Министерство образования и науки Республики Казахстан
Южно-Казахстанский Государственный Университет им М.Ауезова
Факультет: «Промышленное, гражданское и дорожное строительство»
Кафедра: «Строительство»
СРС
На тему: «Элементы геодезических разбивочных работ»
Выполнил: Кулаков Р.
Группа: СМ-10-6р2
Принял: Култаев М.С.
Шымкент 2011 г.
Содержание
1. Элементы геодезических разбивочных работ.
2. Построение в натуре проектных углов.
3. Расстояния проектных отметок.
4. Построение проектных линий.
5. Линии заданного угла.
Лекция 2.
Элементы геодезических разбивочных работ. Построение в натуре проектных углов, расстояний проектных отметок, линий заданного угла.
ЭЛЕМЕНТЫ РАЗБИВОЧНЫХ РАБОТ. ПОСТРОЕНИЕ ПРОЕКТНОГО УГЛА.
Элементами геодезических разбивочных работ принято считать проектные углы, отрезки, точки с проектными отметками, линии проектного уклона, которые необходимо построить для перенесения проекта планировки и застройки с плана на местность.
Для построения проектного угла βпр от линии АВ (рис.59а) на местности приводят теодолит над точкой А в рабочее положение, закрепляют лимб, наводят зрительную трубу на точку В и берут отсчет βкл при КЛ. Затем к этому отсчету прибавляют значение проектного угла, если угол откладывают по ходу часовой стрелки (если против хода часовой стрелки - значение проектного угла вычитают). Вычисленный отсчет устанавливают на горизонтальном круге и на местности закрепляют точку Скл. Действия повторяют при КП и находят точку Скп. Полученный отрезок между точками делят пополам и получают точку С, которая соответствует значению проектного угла. Для контроля построенный угол измеряют способом приемов.

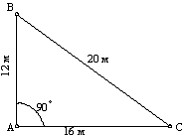
Рис.59.Схема построения проектного угла с помощью теодолита (а) и рулетки (б)
Часто на строительных площадках выполняют построение прямых углов (рис.59б) с помощью рулетки, используя известные свойства "египетского" треугольника с отношением сторон 3:4:5. Для этого от вершины А прямого угла по линии АВ откладывают отрезок кратный 3, например 6 м, и получают точку В. От точек А и В линейными засечками со сторонами соответственно 8 и 10 м получают точку С.
Разбивочные работы
являются одним из основных видов инженерно-геодезической деятельности. Выполняют их для определения на местности планового и высотного положения характерных точек и плоскостей строящегося сооружения в соответствии с рабочими чертежами проекта.
Проект сооружения составляют на топографических планах крупных масштабов. Определяют расположение проектируемого сооружения относительно окружающих объектов и сторон света. Кроме того, топографический план определяет общегеодезическую систему координат, задающую положение характерных точек проектируемого сооружения относительно этой системы.
Разбивочные геодезические работы (вынос проекта в натуру) - это процесс нахождения на местности положения точек сооружения по координатам указанным в проекте.
Компоновка сооружения определяется его геометрией, которая в свою очередь, задается осями. Относительно осей сооружения в рабочих чертежах указывают местоположение всех элементов сооружения.
Различают главные, основные и промежуточные (детальные) оси.
Главными осями линейных сооружений (дороги, каналы и т.д.) служат продольные оси этих сооружений. В промышленном и гражданском строительстве в качестве главных осей принимают оси симметрии зданий.
Основные оси определяют форму и габаритные размеры зданий и сооружений.
Промежуточные, или детальные, оси - это оси отдельных элементов зданий и сооружений.
Указанные в проекте сооружения координаты, углы, расстояния и превышения называют проектными.
Высоты плоскостей и отдельных точек проекта задают от условной поверхности. В зданиях за условную поверхность (нулевую отметку) принимают уровень "чистого пола" первого этажа.
Весь процесс разбивки сооружения определяется общим геодезическим правилом перехода от общего к частному. Разбивка главных и основных осей определяет положение всего сооружения на местности, т.е. его размеры и ориентирование относительно сторон света и существующих контуров местности. Детальная разбивка определяет взаимное положение отдельных элементов и конструкций сооружения.
Разбивочные работы - это комплексный взаимосвязанный процесс, являющийся неотъемлемой частью строительно-монтажного производства, поэтому организация и технология разбивочных работ целиком завист от этапов строительства.
В подготовительный период на местности строят плановую и высотную геодезическую разбивочную основу соответствующей точности, определяют координаты и отметки пунктов этой основы.
Затем производится геодезическая подготовка проекта для перенесения его в натуру. Геодезическая подготовка проекта предусматривает аналитический расчет элементов проекта, геодезическую привязку проекта, составление разбивочных чертежей, разработку проекта производства геодезических работ.
Аналитический расчет элементов проекта заключается в нахождении по значениям проектных размеров и углов в принятой системе проектных координат основных точек сооружений, элементов планирования и благоустройства (осей проездов, коммуникаций, дорог и т.д. Для этого используют основные чертежы проекта: генеральный план, определяющий состав и местоположение сооружения; рабочие чертежи, на которых в крупных масштабах показаны планы, разрезы, профили всех частей сооружения с размерами и высотами деталей; план организации рельефа; планы и профили дорог, подземных коммуникаций.
Привязкой проекта называют расчеты геодезических данных (разбивочных элементов), по которым проект выносят в натуру от пунктов разбивочной геодезической основы или опорных капитальных строений. Разбивочными элементами служат расстояния, углы и превышения, выбор и расчет которых зависят от принятого способа разбивки.
Результаты геодезической подготовки проекта отображают на разбивочных чертежах. Разбивочный чертеж является основным документом, по которому в натуре выполняются разбивочные работы, его составляют в масштабах 1:500 ... 1:2000, а иногда и крупнее в зависимости от сложности сооружения. На разбивочном чертеже показывают: контуры выносимых зданий и сооружений, их размеры и расположение осей, пункты разбивочной основы, разбивочные элементы.
Непосредственную разбивку сооружений выполняют в три этапа. На первом этапе производят основные разбивочные работы. По данным привязки от пунктов геодезической основы находят на местности положение главных и основных разбивочных осей и закрепляют их.
На втором этапе, начиная с возведения фундаментов, проводят детальную строительную разбивку. От закрепленных точек главных и основных осей разбивают продольные и поперечные оси отдельных строительных элементов и частей сооружения, одновременно определяя уровень проектных высот.
Детальная разбивка производится значительно точнее, чем разбивка главных осей, поскольку она определяет взаимное расположение элементов сооружения, а разбивка главных осей - лишь общее положение сооружения и его ориентирование.
Если главные оси могут быть определены на местности со средней квадратической погрешностью 3-5 см, а иногда и грубее, то детальные оси разбивают со средней квадратической погрешностью 2-3 мм и точнее.
Третий этап заключается в разбивке технологических осей оборудования. На этом этапе требуется наибольша точность (в отдельных случаях - доли миллиметра).
Нормы точности на разбивочные работы задаются в проекте или в нормативных документах (СНиП, ГОСТ, ведомственных инструкциях).
Построение проектной линии
При построении проектной линии на производстве учитываются многие требования,
изучаемые в специальных курсах. Проведение проектной линии выполняется из
следующих условий:
1. Объем земляных работ должен быть минимальным.
2. Объем по выемке и по насыпи должен быть приблизительно одинаковым.
3. Фактически уклон не должен превышать руководящий (заданный).
4. Между подъемом (спуском) и спуском (подъемом) должна быть
горизонтальная вставка на менее 200 м.
В графе «Уклоны» ординатами разделяют элементы запроектированной трассы.
Около ординат в этой графе указывают расстояние до ближайших пикетов. Если
перелом проектной линии не совпадает с пикетом, то его обозначают ординатой,
которая, как и проектная линия, вычерчивается красным цветом. Диагоналями или
горизонтальной кривой показывают уклон запроектированного элемента. Над
диагоналями пишется величина уклона в промилле, а под диагоналями –
протяженность подъема или спуска в метрах.
Величины уклонов элементов проектной линии определяют графически. Для этого
строят над профилем треугольник уклонов, у которого основание равно 10 см. В
нашем масштабе оно будет соответствовать 1000 м местности. Если второй катет
построить равным 3 см, то получим гипотенузу с уклоном 3/1000 или иначе 3‰.
Уклон в тысячных долях – это число метров подъема или спуска на 1 км длины.
Чтобы определить величину запроектированного уклона, достаточно сделать
параллельный перенос участка проектной линии на треугольник уклонов и
подсчитать число миллиметров на втором катете. Оно будет соответствовать
запроектированному уклону.
5.2. Определение проектных отметок
Проектная отметка ПК0 определяется графически с профиля . Все остальные
отметки (пикетов и плюсов) определяются аналитически с точностью до см.
Учитывая вертикальный масштаб, но местность проектная отметка будет равна
14,40 м. Проектные отметки любой точки вычисляются с точностью до см
алгебраически по формуле:
H=H0 +i*d,
где H0 - отметка начальной точки данного элемента профиля,
i - величина уклона,
d - расстояние данной точки от начальной.
HПК1 =14,4+0,011*100=15,5 м
и т.д.
проектные отметки на плюсовых точках находят аналогично, только уклон
умножают не на 100 м, а на расстояние до плюсовой точки.
Например: проектная отметка для точки +46 на пикете 3 равна 78,4 м.
Н+46 =15,26+0,011*46=17,46 м, где 15,26 отметка проектная на ПК3.
Рабочие отметки представляют собой разности между проектной и отметкой земли на
каждом пикете и плюсе. Их вычислят с точностью до сантиметра по формуле: Н
раб =Рпр -Нз .
ПК1: Нраб =13,6-15,5= -1,90 м.
Величина рабочей отметки указывает высоту насыпи или глубину выемки.
Выписывают рабочие отметки на профиле красным цветом: для насыпи – над
проектной линией, а для выемок – под ней на расстоянии 1 см.
5.3. Вычисление положения точек нулевых работ
Там, где насыпь переходит в выемку, проектная линия пересекает линию земли,
т.е. рабочая отметка равна 0. Такие точки называются точками нулевых работ.
Их местоположение, т.е. горизонтальное расстояние от ближайшего заднего
пикета или плюса, определяют по формуле
l0
=![]() ,
,
h1 и h2 – рабочие отметки соседних точек профиля,
l – расстояние между этими точками.
Между ПК1 иПК2 l=![]() м.
м.
5.4. Расчет основных элементов разбивки кривых и вставка кривых в пикетаж
По заданию требуется показать в профиле две кривые, направленные в разные
стороны. Для каждой кривой в задании указан угол поворота ![]()
, радиус R кривой, длина переходной кривой l. Кроме того, для первой кривой дано
место положение вершины угла поворота (расстояние от ПК0), для второй кривой
указана прямая вставка перед ней d.
Для контроля вычисляем Дс =2Тс -Кс и это значение
сравниваем с полученным из таблицы.
Пикетажное значение главных точек кривой определяется по формулам
НК=ВУ-Т, СК=НК+0,5Кс , КК=СК+0,5Кс ,
Для контроля:
КК=ВУ+Т-Д,
Где НК – начало кривой,
КК – конец кривой,
ВУ – вершина угла поворота трассы,
СК – середина кривой.
Расчет:
![]() ВУ1 4+97,00
ВУ1 4+97,00
-Тс 2+26,04
НК 2+ 70,96
+Кс 4+49,87
КК1 7+20,83
НК 2+70,96
+0,5Кс 2+24,935
СК 4+93,895
Контроль:
![]() ВУ1 4+97,00
ВУ1 4+97,00
+Тс 2+26,04
7+23,04
-Дс 0+ 2,21
КК1 7+20,83
Если в вершину угла поворота трассы вписывается круговая кривая, то при
вычислениях пикетажа подставляют в формулу Т0 , К0 , Д
0 .
Для расчета пикетажного значения второй кривой необходимо найти пикетажное
значение ВУ2. В задании дана прямая вставка перед второй кривой d, R, l, ![]()
для второй кривой. Аналогично первой кривой выбираем из таблицы все значения
основных элементов кривой и вычисляем суммированные элементы.
Находим пикетажное значение ВУ2 по формуле
ВУ2=КК+ d+Тс2 ,
Где КК – конец первой кривой.
ВУ2=ПК7+20,83+582+186,15=ПК14+88,98
Расчет:
![]() ВУ2 14+88,98
ВУ2 14+88,98
-Тс 1+86,15
НК 13+02,83
+Кс 3+70,53
КК2 16+73,36
НК 13+02,83
+0,5Кс 1+85,265
СК 14+88,095
Контроль:
![]() ВУ2 14+88,98
ВУ2 14+88,98
+Тс 1+86,15
16+75,13
-Дс 0+ 1,78
КК12 16+73,35
5.5. Оформление графы «Условный план линии» в профиле
На расстоянии 2 см вниз от графы «Пикетаж» проводят прямую – ось трассы.
Начало и конец каждой кривой обозначают перпендикулярами, проведенными от
графы «Пикетаж»до оси трассы в соответствии с рассчитанными значениями НК и
КК. Около перпендикуляров пишут расстояние до ближайших пикетов. Сумма этих
расстояний должна быть равна 100 м.
Например, начало первой кривой – на ПК2+70,96, а конец кривой – на ПК7+20,83.
Значит первый перпендикуляр опускают на графу «Пикетаж» на расстоянии 70,96
м. Слева от него пишут красным цветом 70,96, справа – остаток до 100, т.е.
29,04
Чтобы показать конец кривой, второй перпендикуляр опускают на расстоянии
20,83 от ПК7. Слева от него пишут 20,83, справа – 79,17.
Для второй кривой аналогично.
Если начало или конец кривой совпадают с пикетом, о нули. Сами кривые
показывают условными знаками. Кривая изображается двумя четвертями
окружности, описанными радиусом 5 мм в начале и в конце кривой. Полученные
точки соединяют прямой, отстоящей от линии на 5 мм выше или ниже от трассы.
Расположение условного знака кривой зависит от направления поворота трассы.
При повороте трассы направо кривая смотрит выпуклостью вверх, при повороте
трассы налево – кривая вписывается в угол выпуклостью вниз. Над условными
обозначениями кривой о=или под ней пишут длину переходной кривой.
Линии заданного угла
Ориентировать линию – значит определить её направление относительно исходного направления, например, меридиана или оси абсцисс х системы плоских прямоугольных координат.
Угол, измеряемый по ходу часовой стрелки от северного направления меридиана до заданного направления, называется азимутом.
Если исходным направлением служит геодезический меридиан, то азимут называют геодезическим азимутом. Если – астрономический, то - астрономическим азимутом. Обобщением обоих понятий служит термин - географический азимут или просто - азимут.
Значения азимута лежат в пределах от 0° до 360°. На рис. 3.1, а обозначено: С – северное направление меридиана, угол А 1 – азимут направления на точку 1 и А 2 – азимут направления на точку 2.

Рис. 3.1. Углы ориентирования: а - азимуты географические; б - магнитный азимут
На местности азимут заданного направления можно определить астрономическим методом - измерив горизонтальный угол между направлением на небесное светило (Солнце, звезду) и заданным направлением. Зная азимут светила, вычисляемый с использованием астрономического ежегодника, и измеренный угол, соображают азимут заданного направления.
Угол, отсчитываемый от северного направления магнитной стрелки до заданного направления, называется магнитным азимутом.
Магнитная стрелка компаса отклоняется от направления истинного меридиана на угол d, который называется склонением магнитной стрелки (рис. 3.1, б ).
Если северный конец магнитной стрелки отклоняется от меридиана к востоку, то склонение называют восточным и считают положительным, а если - к западу, то называют западным и считают отрицательным.
Азимут с магнитным азимутом связывает формула:
![]()
где А - азимут, А м - магнитный азимут и d – склонение магнитной стрелки.
Магнитные азимуты в геодезии измеряют буссолью (рис. 3.2). Однако точность этих измерений невысока (несколько минут), так как склонение магнитной стрелки непостоянно. На территории России оно меняется от места к месту в пределах от –15° до 25°. В аномальных районах (например, в районе Курской магнитной аномалии) эти изменения так велики, что магнитной стрелкой пользоваться нельзя. Кроме того, склонение изменяется во времени, испытывая суточные, годовые и вековые изменения.
|
|
Рис. 3.2. Буссоль |
Углом ориентирования, применяемым при использовании системы плоских прямоугольных координат Гаусса-Крюгера, является дирекционный угол.
Дирекционным углом называется угол между северным направлением осевого меридиана или линии ему параллельной и заданным направлением (рис. 3.3).
Угол g между северным направлением меридиана и направлением оси абсцисс х прямоугольных координат (то есть линии, параллельной осевому меридиану) называется сближением меридианов .

Рис. 3.3. Углы ориентирования: а - дирекционные углы a1 , a2 ; б - азимут A и дирекционный угол a
При отклонении оси абсцисс от меридиана к востоку, сближение меридианов считают положительным, а при отклонении к западу - отрицательным. При этом справедлива формула (рис. 3.3 б )
А = a + g,
где a - дирекционный угол, g - сближение меридианов.
Приближенно сближение меридианов равно
g = Dl sinj,
где Dl = l-l0 , причем l -долгота географического данной точки и l0 - долгота осевого меридиана; j - широта точки.
На рис. 3.4 показано соотношение между азимутами и дирекционными углами в пределах одной координатной зоны. Легко заметить, что для точек, расположенных к востоку от осевого меридиана зоны, сближение меридианов положительное, а к западу – отрицательное. При этом дирекционные углы в разных точках прямой линии равны a1 = a2 = a3 . Поэтому обратный дирекционный угол в точке 3 отличается от прямого в точке 1 ровно на 180°, то есть a1-3 = a3-1 ± 180°. Азимуты же в разных точках прямой различаются: А1 ¹ А2 ¹ А3 , что обусловлено различием сближения меридианов. Поэтому и А1-3 ¹ А3-1 ± 180°.
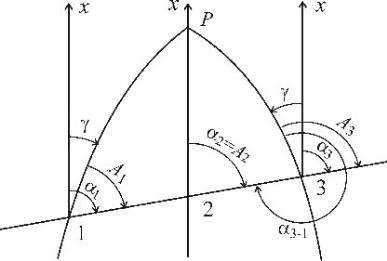
Рис. 3.4. Связь между азимутами и дирекционными углами: 1 – в западной половине зоны; 2 – на осевом меридиане; 3 – в восточной половине зоны; Р – полюс; 1Р , 3Р – меридианы; 2Р – осевой меридиан.
При использовании местной системы прямоугольных координат направление оси абсцисс x не связано с направлением осевого меридиана координатной зоны, и тогда дирекционные углы отсчитывают от положительного направления оси абсцисс х .
В практике вычислений находят применение также вспомогательные углы ориентирования – румбы . Румбом называют острый угол, измеряемый от ближайшего направления меридиана (северного или южного). Румбу приписывают название координатной четверти (СВ, ЮВ, ЮЗ, СЗ), в которой расположено заданное направление. Например, для a = 240°36¢ румб равен r = ЮЗ: 60°36¢.
При вычислительной обработке выполненных на местности измерений, а также при проектировании инженерных сооружений и расчетах для перенесения проектов в натуру возникает необходимость решения прямой и обратной геодезических задач.
Прямая геодезическая задача . По известным координатам х 1 и у 1 точки 1, дирекционному углу a1-2 и расстоянию d 1-2 до точки 2 требуется вычислить ее координаты х 2 , у 2 .
| |
Рис. 3.5. К решению прямой и обратной геодезических задач |
Координаты точки 2 вычисляют по формулам (рис. 3.5):
 (3.4)
(3.4)
где Dх , Dу - приращения координат, равные
 (3.5)
(3.5)
Обратная геодезическая задача . По известным координатам х 1 , у 1 точки 1 и х 2 , у 2 точки 2 требуется вычислить расстояние между ними d 1-2 и дирекционный угол a1-2 .
Из формул (3.5) и рис. 3.5 видно, что
![]() . (3.6)
. (3.6)
Для определения дирекционного угла a1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса
w = ,
,
лежащее в диапазоне -90°£w£+90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a £ 360°.
Формула перехода от w к a зависит от координатной четверти, в которой расположено заданное направление или, другими словами, от знаков разностей Dy = y 2 - y 1 и Dx = х 2 - х 1 (см. таблицу 3.1 и рис. 3.6).
Таблица 3.1
| I четверть |
П четверть |
Ш четверть |
IV четверть |
|
| Dх |
+ |
- |
- |
+ |
| Dу |
+ |
+ |
- |
- |
| w |
+ |
- |
+ |
- |
| Формулы |
a=w |
a=w+180° |
a=w+180° |
a=w+360° |

Рис. 3.6. Дирекционные углы и главные значения арктангенса в I, II, III и IV четвертях
Расстояние между точками вычисляют по формуле
![]() (3.6)
(3.6)
или другим путем – по формулам

![]() (3.7)
(3.7)
Программами решения прямых и обратных геодезических задач снабжены, в частности, электронные тахеометры, что дает возможность непосредственно в ходе полевых измерений определять координаты наблюдаемых точек, вычислять углы и расстояния для разбивочных работ.
Контрольные вопросы
1) Что такое элементы геодезических разбивочных работ?
2) Что называют привязкой проекта?
3) Что учитывают при построении проектной линии?
4) Что называется дирекционным углом?
5) Что значит ориентировать линию?
6) Что называют сближением меридианов?
Литература
Е.Б. Михаленко, Н.Д. Беляев, В.В. Вилькевич, Н.Н. Загрядская, А.А. Смирнов.
СПб.: Изд-во СПбГПУ, 2004
Технология возведения зданий и сооружений

