Курсовая работа: Курсовая работа: Розрахунок диференційної сиcтеми в MatLab

Міністерство освіти та науки України

Національний технічний Університет

“ХПІ”

кафедра “Обчислювальна техніка та програмування”

Звіт

з розрахунково-графічного завдання №1

по курсу

“Комп’ютерне моделювання”

Розрахунок диференційної сиcтеми в MatLab

Виконав:

Перевірив:

Харків

2006.

Зміст

1. Завдання

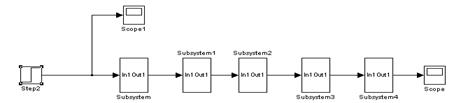
2. Структурна схема об’єкту моделювання

3. Перший блок

4. Другий блок

5. Третій блок

6. Четвертий блок

7. П’ятий блок

8. Рекурентне співвідношення

9. Дослідження моделі на адекватність при заданих типових впливах

10. Висновок

Завдання.

Для виконання розрахункового завдання необхідно висвітити питання які перечисленні нижче.

1). Структурна схема об’єкту, згідно даних варіанту завдання та вихідні дані;

2). Математична модель у вигляді передавальних функцій;

3). Математична модель у вигляді диференційного рівняння;

4). ;

5). Алгоритм рішення (рекурентне співвідношення) та його програмна реалізація в пакеті MATLAB

а) парні варіанти – метод Ейлера,

б) непарні – метод трапецій;

6). Розрахунок необхідної величини (значення) кроку інтегрування отриманого диференційного рівняння згідно заданого методу;

7). Дослідження моделі на адекватність при заданих типових впливах: константа; б-функція; синусоїдальний сигнал; експонента;

8). Аналіз методів рішень системи диференційних рівнянь пакету MATLAB;

9). Результати досліджень;

10).Висновки.

1.Структурна схема об’єкту моделювання

R1	L1	C2			L3

Початкові данні.

Примітка: C(мкФ); L(мГн); R(МОм)

П`ятий блок.

L₃ = 1.6; C₅ = 1.5;

R5	L3

Для отримання структурної схеми використовуємо наступні формули.

Математична модель у вигляді передавальних функцій :

Математична модель у вигляді диференційного рівняння :

Другий блок :

C₂ = 1.3; R₂ =0.2 .

Враховуючи наступні формули отримуємо структурну схему моделі :

Uвх

UВЫХ

Математична модель у вигляді передавальних функцій :

Математична модель у вигляді диференційного рівняння :

Третій блок :

R₃ = 0.3; C₃ = 4.8 L₂ = 0.18;

Враховуючи наступні формули отримуємо структурну схему моделі :

Математична модель у вигляді передавальних функцій :

Математична модель у вигляді диференційного рівняння :

Четвертий блок :

R₄ = 0.7 ; C₄ = 4.0;

R4
				Uвх

Враховуючи наступні формули отримуємо структурну схему моделі :

Математична модель у вигляді передавальних функцій :

Математична модель у вигляді диференційного рівняння :

Розбиваємо дану схему на блоки:

Перший блок :

R₁ = 0.4; L₁ =0.5 ; C₁ = 1.5 ;

Враховуючи наступні формули отримуємо структурну схему моделі :

Математична модель у вигляді передавальних функцій :

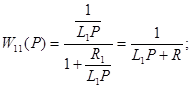
Математична модель у вигляді диференційного рівняння :

5). Алгоритм рішення (рекурентне співвідношення) та його програмна реалізація в пакеті MATLAB

Розроблюемо алгоритм рішення (рекурентне співвідношення) та його програмну реалізацію в пакеті MATLAB метод прямокутників.

Для рішення використаемо частину схеми яка мае математичну модель у вигляді диференційного рівняння :

Для запису рекурсивного співвідношення може бути використоване підхід який обгрунтован на Z перетворенні та операторного методу при учете співідношення.

Записуемо діференційне рівняння у термінах D та I.

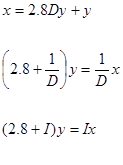
Замість параметру інтегрування підставимо:

Розділимо отримане рівняння на найвищу степінь z.

Рекуррентное співвідношення має вигляд:

Дослідження моделі на адекватність при заданих типових впливах:

Для дослідження моделі на адекватність використаємо сигнал типу константа;

Мал 1.

В результаті подання сигналу на вход схеми був отриман вихідний сигнал який зображений на малюнку

Мал. 2

Виходячи з отриманого графіку можна зробити висновок, що вихідний сигнал сходиться.

2) Подамо на вхід схеми сигнал у вигляді б-функцій;

Мал.3

В результаті на виході схеми отримаемо сигнал який має свойства сходження

Даний сигнал зображений на малюнку 4;

Мал.4

3) Подамо на вхід схеми, сигнал у вигляді синусоїди

При подачі на вхід схеми, сигналу у вигляді синусоїди отримаємо вихідний сигнал

ал.5

У результаті отримаємо на виході сигнал який має свойство несходження.

Даний сигнал зображений на малюнку 6;

Мал.6

4) Подамо на схему сигнал у вигляді експонента;

Мал.7

На виході отримаємо сигнал який зображений на малюнку 8

мал.8

Висновок:

В результаті виконання данної роботи були проведені розробка схеми дослідження, побудовані математични моделі частин схеми, а також проаналізована робота схеми при подачі різних сигналів.