| Скачать .docx |
Курсовая работа: Построение реалистических изображений поверхности океана с 3хмерной лодки, которая плавает по поверхности океана
Курсовая работа
по машинной графике
На тему: Построение реалистических изображений поверхности океана с 3хмерной лодки, которая плавает по поверхности океана
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
1. ВВЕДЕНИЕ
1.1. Современные алгоритмы машинной графики
1.2. Рекурсивные алгоритмы построения изображения
1.3. Назначение программы
2. КОНСТРУКТОРСКИЙ РАЗДЕЛ
2.1. Выбор и обоснование используемых алгоритмов
2.2. Базовые алгоритмы
2.2.1. Алгоритм обратной трассировки лучей
2.2.2. Глобальная модель освещения Уиттеда
2.2.3. Стохастический суперсэмплинг
2.2.4. Шум Перлина
2.3.Система координат
2.4. Объекты сцены
2.4.1. Солнце
2.4.2. Лодка
2.4.3. Водная поверхность
2.5.Базовые трехмерные объекты
2.5.1. Сфера
2.5.2. Треугольник
2.6. Текстура и фактура
2.6.1. Общие сведения
2.6.2. Наложение текстуры на треугольник
2.6.3. Фактура
3. ТЕХНОЛОГИЧЕСКИЙ РАЗДЕЛ
3.1. Выбор и обоснование языка и среды программирования
3.2. Структура классов программы
3.2.1. Математические абстракции
3.2.2. Вспомогательные классы свойств трехмерных объектов
3.2.3. Базовые трехмерные объекты
3.2.4. Источник света
3.2.5. Сцена
3.2.6. Алгоритмы визуализации
3.2.7. Классы интерфейса
3.3. Пользовательский интерфейс
3.3.1. Главное меню
3.3.2. Диалог установки размера изображения
3.3.3. Диалог установки параметров сцены
3.3.4. Диалог установки параметров камеры
3.4. Условия применения программы
3.5. Обращение к программе
3.6. Входные и выходные данные
3.7. Сообщения
4. ЭКСПЕРИМЕНТАЛЬНО-ИССЛЕДОВАТЕЛЬСКИЙ РАЗДЕЛ
4.1. Описание экспериментов
4.2. Результаты экспериментов
5. ЗАКЛЮЧЕНИЕ
6. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Приложение 1
1. ВВЕДЕНИЕ
1.1 Современные алгоритмы машинной графики
В настоящее время вопросы, связанные с отображением на экране дисплея разнообразных изображений, как никогда актуальны. Графика используется практически во всех областях деятельности человека, так или иначе связанных с использованием компьютера. Графическое представление информации может быть как всего лишь более удобным средством представления информации и организации взаимодействия пользователя с вычислительной машиной, так и неотъемлемой частью вычислительного комплекса, например, при моделировании сложных процессов, природных явлений, реалистичной графики в трехмерных компьютерных играх.
До недавнего времени основным критерием выбора способа отображения трехмерных объектом являлась скорость вычислений, в силу того, что мощности компьютеров не хватало для полноценной реализации существующих алгоритмов.
Примером таких «быстрых» алгоритмов являются алгоритмы, такие как z-буфер, использующие построчный просчет видимого изображения; эти методы давали вполне приемлемую скорость и до сих пор используются в ряде случаев, когда на первом месте стоит быстродействие. Однако они имеют один существенный недостаток, который в ряде случаев сводит на нет их преимущества: с их помощью невозможно построить высокореалистичные изображения с отображением таких оптических эффектов, как отражение, преломление, блики света от воды и т.д. Были попытки сымитировать подобные эффекты, накладывая на объекты, заранее просчитанные текстуры освещенности, что в совокупности с эффективными алгоритмами оптимизации несколько приближало изображение к реальности. Такой подход широко использовался в трехмерных компьютерных играх и был доведен разработчиками практически до совершенства. Однако того качества изображения, которое может быть получено с применением рекурсивных алгоритмов, таких как прямая и обратная трассировка лучей, а также алгоритм излучательности, им никогда не достичь.
1.2 Рекурсивные алгоритмы построения изображения
Для получения действительно реалистичных изображений, сравнимых с фотографией, в настоящее время существует три алгоритма: алгоритм прямой трассировки лучей, алгоритм обратной трассировки лучей и алгоритм излучательности.
Алгоритм прямой трассировки лучей разработан уже давно, но, как и в момент его создания, в настоящее время он применяется очень мало в силу исключительно больших вычислительных затрат и существенной избыточности вычислений. Кроме того, очень трудно предсказать время вычисления, которое может оказаться неприемлемо большим. Однако алгоритм все же используется, поскольку качество и реалистичность получаемого изображения очень высоки.
Алгоритм обратной трассировки лучей в той или иной модификации является основным средством получения высокореалистичных изображений с большинством возможных оптических эффектов, наблюдаемых в реальной жизни. Результат работы алгоритма оказывается очень близким к реальности. В настоящее время обратная трассировка лучей становится все более популярной, и существует тенденция применения модификаций этого алгоритма в программах, требующих построения трехмерных изображений в реальном времени, например, в компьютерных играх. Это стало возможным благодаря тому, что данный алгоритм естественным образом распараллеливается и, таким образом, в полной мере может использоваться многопроцессорными системами.
Еще одним рекурсивным алгоритмом построения реалистических изображений, принципиально отличающимся от перечисленных, является алгоритм излучательности. В отличие от трассировки лучей, основанной на принципах геометрической оптики, данный метод использует законы сохранения энергии, что позволяет моделировать сцену физически соответствующую реальности. Алгоритм излучательности обычно используется в комбинации с обратной трассировкой лучей.
1.3 Назначение программы
Данная программа предназначена для построения реалистических изображений поверхности воды с трехмерным объектом на ней. В ее основе лежит алгоритм обратной трассировки лучей, включающий в себя поддержку отражения и преломления лучей, а также учет таких оптических эффектов, как блики от солнца, и различных волнений водной поверхности. Дополнительно реализованы такие алгоритмы, как наложение текстуры, отображение фактуры поверхности, устранение «лестничного» эффекта по алгоритму стохастического суперсэмплинга.
Сцена состоит из водной поверхности, трехмерной лодки и солнца. Пользователь имеет возможность редактировать размеры лодки, ее положение в пространстве. Освещенность сцены и положение солнца рассчитываются в зависимости от введенных пользователем параметров: дата, время и географическое положение. Программа может, как строить один кадр сцены, так и последовательность кадров (мультипликация), когда лодка движется в зависимости от направления и скорости ветра.
2. КОНСТРУКТОРСКИЙ РАЗДЕЛ
2.1 Выбор и обоснование используемых алгоритмов
Базовым алгоритмом при разработке данной программы был выбран алгоритм обратной трассировки лучей. Основным его преимуществом является получение намного более реалистичных изображений, чем при применении алгоритмов, таких как алгоритм z-буфера. Высокая реалистичность достигается потому, что алгоритм основан на законах оптики и может воспроизводить эффекты, недоступные другим алгоритмам – отражение, преломление и точные тени. Кроме того, алгоритм обратной трассировки учитывает специфику свойств материалов отображаемых объектов.
К преимуществам алгоритма можно отнести также невысокую потребность в памяти, потому что при построении изображения интенсивность каждого пиксела вычисляются автономно, и память расходуется только на хранение текущего дерева луча.
Основным недостатком алгоритма обратной трассировки лучей является его крайне низкая скорость, однако процесс вычисления очевидным образом распараллеливается, что делает возможным расчет различных участков изображения на отдельных процессорах или даже компьютерах в сети. Таким образом, можно достигнуть скорости прорисовки, близкой к реальному времени.
Для расчета интенсивности каждого пиксела используется глобальная модель освещения Уиттеда, как проверенная временем и позволяющая получить близкое к реальности изображение, в то же время, давая приемлемую скорость, в отличие, например, от глобальной модели Холла, учитывающей зависимость коэффициентов диффузного и френелевского отражения, а также коэффициента френелевского пропускания от длины волны и свойств вещества
Для моделирования водной поверхности взят алгоритм наложения фактуры (bump-mapping). Сама фактура генерируется с помощью шума Перлина, который затем интерполируется с помощью функции косинусов. Данный алгоритм позволяет достичь наибольшего быстродействия и дает приемлемые результаты для больших водных поверхностей (море, океан), в то время как другие алгоритмы (быстрые преобразования Фурье (FFT), дифференциальные уравнения движения водных потоков, фракталы) требуют, как больших вычислительных затрат при расчете, так и аппроксимации водной поверхности множеством примитивов, что приводит к огромным затратам по времени и неприемлемы для программной реализации.
Для повышения реалистичности изображаемых объектов используются алгоритмы текстурирования и фактурирования. Применяя их, можно добиться почти фотографической реалистичности прорисовки поверхности объекта.
Еще одним добавлением к базовому алгоритму трассировки является стохастический суперсэмплинг, позволяющий устранить неровности на границах объектов гораздо эффективнее, чем обыкновенно применяемый для устранения “лестничного” эффекта суперсэмплинг. Данный подход показывает неплохие результаты даже при пропускании всего одного луча на пиксел.
2.2 Базовые алгоритмы
2.2.1 Алгоритм обратной трассировки лучей
Идея алгоритма обратной трассировки лучей унаследована от придуманного ранее алгоритма прямой трассировки лучей. Суть алгоритма в испускании из точки наблюдения луча через каждую точку картинной плоскости и определение интенсивности этой точки путем отслеживания маршрута испущенного луча, который ведет себя по законам геометрической оптики. Алгоритм рекурсивен – при попадании на поверхность объекта луч делится на отраженный и преломленный и продолжает свой путь. Таким образом, можно построить дерево хода луча, где узел является пересечением луча с поверхностью, а исходящие из узла ветви – отраженный и преломленный лучи. Ветвь кончается, когда поиск пересечения соответствующего луча с объектами сцены дает отрицательный результат. Однако при таком подходе легко получить бесконечную рекурсию – в случае, например, расположенных друг напротив друга идеальных зеркал луч будет отражаться от них бесконечно. Для предотвращения подобных эффектов, а также для повышения скорости вычислений вводят предельное значение глубины рекурсии, представляющее собой максимальное количество узлов в дереве луча.

При пересечении луча с поверхностью направления отраженного и преломленного лучей определяются, исходя из законов геометрической оптики.
Отраженный луч строится, исходя из того, что падающий луч, отраженный и нормаль к поверхности в точке касания лежат в одной плоскости, и угол падения равен углу отражения (рис. 2.1).
|
![]() (2.1)
(2.1)
Для преломленного луча используется закон Снеллиуса, который гласит, что отношение синусов углов падения и отражения равно отношению абсолютных коэффициентов преломления сред (рис. 2.2).
Преломление луча

Рис. 2.2 Вектор преломленного луча вычисляется по формулам /8/:
 (2.2)
(2.2)
Где
 (2.3)
(2.3)
Необходимо заметить, что основной сложностью алгоритма обратной трассировки лучей является нахождения точки пересечения луча с объектом сцены и определение нормали к поверхности в этой точке. Данный вопрос подробно рассматривается в разделе 2.3.
2.2.2 Глобальная модель освещения Уиттеда
Определение интенсивности точки на поверхности объекта осуществляется согласно глобальной модели освещения Уиттеда:
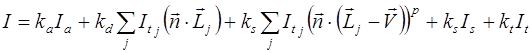 (2.4)
(2.4)
где ![]() ,
, ![]() ,
, ![]() – соответственно, коэффициенты рассеянного, диффузного и зеркального отражения,
– соответственно, коэффициенты рассеянного, диффузного и зеркального отражения, ![]() - коэффициент пропускания.
- коэффициент пропускания.
Глобальная модель освещения Уиттеда

Рис. 2.3
Из рис. 2.3 виден смысл входящих в формулу величин. Трассируемый луч ![]() отражается от поверхности в направлении
отражается от поверхности в направлении ![]() и преломляется (если коэффициент пропускания не равен нулю) в направлении
и преломляется (если коэффициент пропускания не равен нулю) в направлении ![]() . В таком случае интенсивность
. В таком случае интенсивность ![]() в точке поверхности, на которую упал трассируемый луч, будет складываться из интенсивности фонового освещения
в точке поверхности, на которую упал трассируемый луч, будет складываться из интенсивности фонового освещения ![]() , интенсивностей
, интенсивностей ![]() и
и ![]() за счет света, пришедшего с направлений соответственно отраженного и преломленного луча, а также диффузной и зеркальной составляющей от каждого источника света (
за счет света, пришедшего с направлений соответственно отраженного и преломленного луча, а также диффузной и зеркальной составляющей от каждого источника света (![]() - направление на
- направление на ![]() -й источник), причем здесь учитывается не точное направление отражения луча от источника, а так называемое glossiness, или распределенное отражение – распределение отраженного света в некотором телесном угле, обусловленное микрорельефом (шероховатостью) поверхности и визуально наблюдаемое в виде светового блика, имеющего тем большие размеры, чем выше шероховатость поверхности. При определении интенсивности
-й источник), причем здесь учитывается не точное направление отражения луча от источника, а так называемое glossiness, или распределенное отражение – распределение отраженного света в некотором телесном угле, обусловленное микрорельефом (шероховатостью) поверхности и визуально наблюдаемое в виде светового блика, имеющего тем большие размеры, чем выше шероховатость поверхности. При определении интенсивности ![]() - го источника света
- го источника света ![]() учитывается ослабление света при условии нахождения между рассматриваемой точкой поверхности и
учитывается ослабление света при условии нахождения между рассматриваемой точкой поверхности и ![]() - ым источником полупрозрачных тел: в этом случае интенсивность ослабляется путем умножения ее на коэффициент затенения (shading), прямо зависящий от коэффициента пропускания тела. Если же между источником света и точкой лежат непрозрачные объекты, данный источник игнорируется.
- ым источником полупрозрачных тел: в этом случае интенсивность ослабляется путем умножения ее на коэффициент затенения (shading), прямо зависящий от коэффициента пропускания тела. Если же между источником света и точкой лежат непрозрачные объекты, данный источник игнорируется.
В уравнении Уиттеда интересен член:
 (2.5)
(2.5)
где ![]() - это, фактически, косинус угла между направлением отраженного луча от
- это, фактически, косинус угла между направлением отраженного луча от ![]() -го источника света и направлением на точку испускания базового трассируемого луча
-го источника света и направлением на точку испускания базового трассируемого луча ![]() . Этот член уравнения Уиттеда обуславливает отображение бликов на поверхности тела, однако он не имеет ничего общего с физическими законами и был эмпирически получен Фонгом. Степень p, в которую возводится упомянутый выше косинус, называется коэффициентом Фонга и определяет пространственное распределение отраженного света.
. Этот член уравнения Уиттеда обуславливает отображение бликов на поверхности тела, однако он не имеет ничего общего с физическими законами и был эмпирически получен Фонгом. Степень p, в которую возводится упомянутый выше косинус, называется коэффициентом Фонга и определяет пространственное распределение отраженного света.

На рис. 2.4 изображена функция ![]() . Видно, что чем больше коэффициент p, тем меньше по размерам будет блик и тем ближе визуально будет материал к идеальному зеркалу.
. Видно, что чем больше коэффициент p, тем меньше по размерам будет блик и тем ближе визуально будет материал к идеальному зеркалу.
2.2.3 Стохастический суперсэмплинг
Для повышения реалистичности изображения требуется сглаживание резких переходов цвета на границах между объектами. Путем сравнения изображений полученных без алгоритмов устранения ступенчатости и с ними, был сделан вывод, что применение алгоритмов сглаживания значительно повысило качество изображения и приблизило его к реальности.
|

Классическим подходом при решении задачи устранения ступенчатости применительно к обратной трассировке лучей является пропускание через каждый пиксел картинной плоскости не одного, а нескольких лучей, а затем усреднение полученных интенсивностей для получения интенсивности видимого пиксела.
Этот метод получил название суперсэмплинга (supersampling – название пришло из области обработки сигналов и означает повышение частоты дискретизации для получения более качественных результатов). На рис. 2.5 видно, что через каждый пиксел пропускается 9 лучей, что означает увеличение времени вычисления в 9 раз.
Известен такой факт, что световые рецепторы на сетчатке человеческого глаза расположены нерегулярно, на случайных расстояниях друг от друга, но не меньше какого-то определенного расстояния. Это послужило дальнейшему развитию алгоритма суперсэмплинга.

После вычисления координат субпикселов к каждому из них применяется небольшое случайное отклонение, после чего через полученные точки пропускаются лучи, и интенсивности усредняются. Этот подход дал более качественное изображение и получил название стохастического суперсэмплинга (рис. 2.6).
Интересен тот факт, что данный метод дает положительные результаты даже при использовании его при пропускании только одного луча на пиксел – в этом случае «лестничный» эффект все равно устраняется. Хотя при внимательном рассмотрении видны неровности на границах перехода цветов, но зрительно изображение выглядит качественней, чем при построении без использования этого метода.
2.2.4 Шум Перлина
Данный алгоритм используется для моделирования неровностей водной поверхности. Шум Перлина генерирует процедурную фактуру, которая затем накладывается на поверхность.
Функция шума

Рис 2.7
Базовое понятие шума Перлина – это функция шума. Функция шума получает целое число как параметр и возвращает случайное число исходя из него. Причем, если передать тот же самый параметр еще раз, будет получено то же самое число.
Интерполирование функции

Рис 2.8
Интерполированием и сглаживанием можно получить непрерывную функцию, которая определена для действительных чисел.
Для водной поверхности нам нужна 2х мерная функция шума /9/:
![]() (2.6)
(2.6)

Для интерполяции используем косинусную интерполяцию:
 , (2.7)
, (2.7)
где a,b – два параметра, между которыми мы производим интерполяцию
x - число, от которого зависит результат, если x=0 то возвращается
a, если x=1, то возвращается b
2.3 Система координат
В программе принята следующая система координат: ось (ох) показывает на север, ось (oy) направлена вертикально вверх, ось (oz) направлена на запад.
2.4 Объекты сцены
2.4.1 Солнце
Солнце на сцене является сферой, и задается расстоянием от начала координат(удаленность) радиусом сферы, а также направляющим вектором.
Определение единичного направляющего вектора углового положения Солнца происходит на основе даты, времени, широты и угла между осью Х и направлением на юг. Учитывая, что Земля совершает сложное движение, которое складывается из вращательного движения вокруг своей оси и движения вокруг Солнца по почти круговой орбите, можно получить следующие соотношения для координат искомого вектора /7/:
 (2.8)
(2.8)
где ![]() , здесь
, здесь ![]() ,
,
![]() , n – число дней, прошедших с 21 марта,
, n – число дней, прошедших с 21 марта,
![]() , здесь k – число часов, прошедших с 700
,
, здесь k – число часов, прошедших с 700
,
δ – широта,
θ – угол между осью Х и направлением на юг.
Для определения максимальной интенсивности солнца используется следующая формула:
![]() (2.9)
(2.9)
где y –ордината единичного направляющего вектора положения солнца.
Данная формула получена чисто императивно.
2.4.2 Лодка
Параметры лодки

Рис. 2.9
Лодка задается следующими параметрами: длина, ширина, высота борта, длина носа, высота мачты, ширина и высота паруса (см. рис. 2.9).
Мачта лодки имеет квадратное сечение, с длиной стороны равной ![]() длины лодки. Мачта смещена от середины лодки назад на половину ширины паруса.
длины лодки. Мачта смещена от середины лодки назад на половину ширины паруса.
Перемещение лодки определяется по следующей формуле:
![]() (2.10)
(2.10)
где ![]() – скорость ветра
– скорость ветра
t - интервал времени между кадрами
![]() - угол между направлением лодки и направлением ветра.
- угол между направлением лодки и направлением ветра.
Если ветер дует в другую сторону ![]() <0, то лодка стоит и не двигается.
<0, то лодка стоит и не двигается.
2.4.3 Водная поверхность
Для водной поверхности можно задавать только цвет воды. На сцене она представлена как бесконечно большой прямоугольник, центр которого находится в точке (0,0,0). На этот прямоугольник накладывается фактура воды.
2.5 Базовые трехмерные объекты
2.5.1 Сфера
Сфера является одной из наиболее просто аналитически задаваемых объектов. В программе для ее определения хранятся координаты ее центра и длина радиуса.
Задача поиска пересечения луча со сферой достаточно проста и позволяет определить факт отсутствия пересечения на ранних этапах вычисления, что приводит к уменьшению времени выполнения программы и позволяет применять сферу в качестве объемной оболочки объекта, вычисление пересечения луча с которым требует больших вычислительных затрат.
На рис. 2.10 изображена сфера и два пересекающих ее луча, начало одного из которых лежит внутри сферы, а другого – снаружи. Задачу можно рассматривать как плоскую – нахождение пересечения луча с окружностью, в силу того, что через прямую, вдоль которой распространяется луч, и центр окружности, всегда можно провести плоскость, а линия пересечения сферы с плоскостью, проходящей через ее центр, является окружностью с радиусом, равным радиусу самой сферы.
Нахождение точки пересечения луча со сферой

Рис. 2.10
Рассмотрим первый случай, когда начало луча лежит вне сферы – в точке ![]() , направление луча определено единичным вектором
, направление луча определено единичным вектором ![]() . Чтобы найти точку пересечения, достаточно определить расстояние до нее от начала луча в направлении хода луча, то есть длину отрезка
. Чтобы найти точку пересечения, достаточно определить расстояние до нее от начала луча в направлении хода луча, то есть длину отрезка ![]() . Зная координаты центра окружности
. Зная координаты центра окружности ![]() , можно определить вектор
, можно определить вектор ![]() , а затем и скалярное произведение
, а затем и скалярное произведение ![]() , численно равное длине отрезка
, численно равное длине отрезка ![]() . Если скалярное произведение получилось отрицательным или равным нулю – луч заведомо не пересекает сферу и дальнейшие проверки не производятся.
. Если скалярное произведение получилось отрицательным или равным нулю – луч заведомо не пересекает сферу и дальнейшие проверки не производятся.
Иначе находим расстояние от центра сферы до луча – длину отрезка ![]() . В треугольнике
. В треугольнике ![]() , зная длины
, зная длины ![]() и
и ![]() , можно найти длину отрезка
, можно найти длину отрезка ![]() . Здесь производится следующая проверка: если
. Здесь производится следующая проверка: если ![]() (являющийся расстоянием от центра сферы до луча) больше радиуса сферы, луч сферу не пересекает.
(являющийся расстоянием от центра сферы до луча) больше радиуса сферы, луч сферу не пересекает.
Из треугольника ![]() можно аналогичным образом получить длину отрезка
можно аналогичным образом получить длину отрезка ![]() , вычитая который из известного уже отрезка
, вычитая который из известного уже отрезка ![]() , получаем искомое расстояние. Если оно меньше или равно нулю, значит, начало луча лежит на поверхности сферы или же внутри нее (случай луча с началом в
, получаем искомое расстояние. Если оно меньше или равно нулю, значит, начало луча лежит на поверхности сферы или же внутри нее (случай луча с началом в ![]() ), тогда искомое расстояние вычисляется путем сложения длин отрезков
), тогда искомое расстояние вычисляется путем сложения длин отрезков ![]() и
и ![]() .
.
Нормаль к поверхности в любой точке сферы вычисляется тривиальным образом как вектор, соединяющий центр сферы с точкой на поверхности.
2.5.2 Треугольник
Треугольник является примитивом, посредством которого могут быть составлены практически любые многогранные тела. Он задается точкой ![]() – одной из вершин треугольника – и двумя векторами
– одной из вершин треугольника – и двумя векторами ![]() и
и ![]() , определяющими ориентацию и длины его сторон (см. рис. 2.11).
, определяющими ориентацию и длины его сторон (см. рис. 2.11).
Треугольник

Рис.2.11 Пересечение луча с плоскостью

Рис. 2.12
Поиск пересечения луча с треугольником состоит из двух этапов: поиск пересечения луча с плоскостью треугольника и определение нахождения точки внутри него.
Первый этап, изображенный на рис. 2.12, достаточно прост; производится проверка, пересекает ли луч плоскость, путем сравнения с нулем скалярного произведения ![]() . Если оно больше или равно нулю, пересечение отсутствует, и дальнейшие действия можно не выполнять. Вектор, соединяющий произвольную точку плоскости (в данном случае это угол треугольника) с началом луча, проецируется на нормаль и делится на косинус угла между направлением луча и нормалью.
. Если оно больше или равно нулю, пересечение отсутствует, и дальнейшие действия можно не выполнять. Вектор, соединяющий произвольную точку плоскости (в данном случае это угол треугольника) с началом луча, проецируется на нормаль и делится на косинус угла между направлением луча и нормалью.
Таким образом, расстояние от источника луча до точки пересечения равно:
 (2.11)
(2.11)
Второй этап, заключающийся в определении принадлежности точки треугольнику, существенно сложнее и потребует дополнительных рассуждений.
Локальная система координат

Рис. 2.12Введем локальную систему координат ![]() , в которой оси направлены вдоль сторон, причем в пределах треугольника координаты меняются на величину в диапазоне от 0 до 1 и лежат в заштрихованной области (см. рис. 2.12)
, в которой оси направлены вдоль сторон, причем в пределах треугольника координаты меняются на величину в диапазоне от 0 до 1 и лежат в заштрихованной области (см. рис. 2.12)
Для этого введем дополнительные переменные:
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
На основании формул (2.13) и (2.14) введем значение координат в точке плоскости треугольника следующим образом:
 (2.17)
(2.17)
где ![]() - радиус-вектор точки
- радиус-вектор точки ![]() на плоскости, содержащей треугольник. Тогда координаты в исходной точке
на плоскости, содержащей треугольник. Тогда координаты в исходной точке ![]() будут равны:
будут равны:
 (2.18)
(2.18)
где ![]() - радиус-вектор точки
- радиус-вектор точки ![]() .
.
В силу того, что радиус-вектор точки внутри треугольника может быть представлен в виде суммы радиус-вектора точки ![]() и линейной комбинации векторов
и линейной комбинации векторов ![]() и
и ![]() , можем записать разницу координат между произвольной точкой
, можем записать разницу координат между произвольной точкой ![]() внутри треугольника и исходной точкой
внутри треугольника и исходной точкой ![]() :
:
![]()
![]()
Окончательно:
![]() (2.19)
(2.19)
Аналогичным образом можно получить:
![]() (2.20)
(2.20)
Так как ![]() и
и ![]() являются множителями в линейной комбинации векторов
являются множителями в линейной комбинации векторов ![]() и
и ![]() , дающей в результате вектор, конец которого лежит внутри треугольника, если начало привести в точку
, дающей в результате вектор, конец которого лежит внутри треугольника, если начало привести в точку ![]() , то
, то ![]() и
и ![]() меняются в пределах от 0 до 1. Тогда, поделив полученные в формулах (2.19) и (2.20) разницы на величину:
меняются в пределах от 0 до 1. Тогда, поделив полученные в формулах (2.19) и (2.20) разницы на величину:
![]() (2.21)
(2.21)
мы получим требуемый результат – локальные координаты в пределах треугольника меняются не более чем на единицу.
Окончательно имеем формулы для относительных локальных координат:
 (2.22)
(2.22)
Подставляя найденные на первом этапе координаты точки на плоскости в эти выражения и проверив полученные результаты на нахождение в интервале ![]() и условию
и условию ![]() , можно сказать, лежит ли точка внутри треугольника, или нет.
, можно сказать, лежит ли точка внутри треугольника, или нет.
Нормаль к треугольнику в любой его точке определяется как векторное произведение векторов, задающих его стороны.
2.6 Текстура и фактура
2.6.1 Общие сведения
В данной программе предусмотрено наложение на трехмерные объекты текстур и имитация шероховатостей поверхностей. Для этого предусмотрена загрузка битовых карт формата *.bmp из внешних файлов.
Основное отличие фактуры от текстуры – фактура вызывает изменение направления нормали для данной поверхности
2.6.2 Наложение текстуры на треугольник
Для установления соответствия пиксела объекта с пикселом битовой карты необходимо включить точку в формулы (2.22) и, найдя относительные локальные координаты этой точки внутри четырехугольника, определить искомое соответствие, вводя дополнительные множители кратности текстуры.
Этот процесс можно упростить, если принять, что точка ![]() , задающая одну из его вершин и являющаяся точкой отсчета при работе с ними, находится в начале координат. Теперь, зная единичные вектора направления сторон
, задающая одну из его вершин и являющаяся точкой отсчета при работе с ними, находится в начале координат. Теперь, зная единичные вектора направления сторон ![]() и
и ![]() и соответствующие им кратности повторения текстуры
и соответствующие им кратности повторения текстуры ![]() и
и ![]() , можем определить координаты заданной точки на битовой карте:
, можем определить координаты заданной точки на битовой карте:
 (2.23)
(2.23)
где ![]() – радиус-вектор точки
– радиус-вектор точки ![]() .
.
2.6.3 Фактура
Фактурирование – это метод моделирования неровностей изображаемой поверхности без фактического изменения формы модели и с весьма небольшими вычислительными затратами. Фактуры задается битовой картой высот, где участки с высокой интенсивностью означают выпуклости на поверхности, а участки с низкой интенсивностью – впадины.
Фактически метод фактурирования заключается в изменении направления нормали в точке на определенное значение, которое позволяет зрительно исказить поверхность, направив в другую сторону отражение, преломление и блики. Изначальный алгоритм фактурирования предусматривал влияние на результирующую нормаль источника света, однако в данной программе сделано приближение, давшее результат, близкий к реальности: в нормаль вносятся изменения только по осям (ox) и (oz) на величины, не зависящие от источника света.
Для нахождения этих величин сначала необходимо установить соответствие между точкой на поверхности объекта и точкой на битовой карте высот, это осуществляется по алгоритмам, описанным в разделах 2.5.2 – 2.5.3. Затем определяются интенсивности пикселов карты высот, соседних с полученным: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Теперь можно определить значения смещений по осям:
. Теперь можно определить значения смещений по осям:
 (2.24)
(2.24)
Коэффициент A задает зависимость отклонения нормали от внешнего воздействия- в нашем случае ветра.
![]() (2.25)
(2.25)
где v – скорость ветра.
Данная формула получена эмпирически и дает наиболее близкие к реальности результаты.
3. ТЕХНОЛОГИЧЕСКИЙ РАЗДЕЛ
3.1 Выбор и обоснование языка и среды программирования
В настоящее время существует множество языков и сред программирования, многие из которых обладают достаточно высокой эффективностью, удобством и простотой в использовании. Однако при разработке данной программы использовался язык C++ по следующим причинам:
· Этот язык предоставляет программисту широкие возможности реализации самых разнообразных алгоритмов, обладая высокой эффективностью и значительным набором стандартных классов и процедур.
· С++ является одним из немногих языков, в полной мере реализующих концепции объектно-ориентированного программирования, позволяющие использовать множественное наследование, абстрактные и параметризованные классы и т.д. Кроме того, трехмерные объекты, также как и математические абстракции, естественным образом представляются в виде объектов классов, что позволяет легко и эффективно организовывать их взаимодействие, при этом сохраняя читаемый и легко изменяемый код. Здесь же следует отметить такое немаловажное свойство объектно-ориентированного подхода, как повторное использование кода. Большая часть из перечисленных преимуществ C++ отсутствует в таких популярных языках, как Pascal и Basic.
В качестве среды разработки была выбрана MicrosoftVisualStudio 6.0:
· Для этой среды есть специальный компилятор фирмы Intel, который поддерживает очень мощную оптимизацию программы для процессоров вплоть до Pentium 4, что позволило резко повысить быстродействие программы.
· При разработке программы использовались библиотеки классов MFC (MicrosoftFoundationClasses), поставляемые вместе со средой разработки, которые позволяют существенно упростить разработку интерфейса программы по сравнению с использованием стандартных функций WindowsAPI.
· Данная среда обладает удобным редактором кода и отладчиком, предоставляющими большое количество функций, необходимых для эффективного написания исходного кода и локализации и устранения ошибок в программе.
3.2 Структура классов программы
В силу того, что при написании программы использовалась технология объектно-ориентированного программирования, особое внимание при рассмотрении ее структуры должно быть уделено структуре ее классов.
Условно все классы, присутствующие в программе, можно разделить на несколько частей по выполняемым функциям:
· Математические абстракции
· Вспомогательные классы свойств трехмерных объектов
· Базовые трехмерные объекты
· Источник света
· Сцена
· Алгоритмы визуализации
· Интерфейс пользователя
3.2.1 Математические абстракции
Математические абстракции в программе представлены тремя классами:
1. CVector – трехмерный вектор и операции над ним. Реализованы операции умножения на вектор, умножения на матрицу, умножения и деления на число, нахождение скалярного и векторного произведения, нормализации, определение длины. Некоторые операции продублированы операторами для удобства записи, а также введены операторы действий, совмещенных с присваиванием.
2. CMatrix – двумерная матрица 4х4, используемая в программе для задания трехмерных преобразований. Среди реализованных операций: умножение и деление на число, умножение на вектор и на другую матрицу, нахождение обратной и транспонированной матрицы. В класс матрицы включены статические методы, возвращающие матрицы преобразований: поворота, сдвига и масштабирования.
3. CRay – трехмерный луч, задающийся двумя трехмерными векторами: точкой испускания и направлением. Помимо стандартных методов-аксессоров обладает методом сдвига на заданную величину в направлении своего хода, что активно применяется в ходе выполнения алгоритма обратной трассировки лучей.
3.2.2 Вспомогательные классы свойств трехмерных объектов
Одним из основных классов, задающих внешний вид трехмерного объекта, является класс CSurface, среди атрибутов которого присутствуют следующие величины:
· Коэффициент фоновой освещенности
· Коэффициент диффузного отражения
· Коэффициент зеркального отражения
· Коэффициент Фонга (характеризует пространственное распределение зеркально отраженного света)
· Коэффициент прозрачности
· Коэффициент преломления
· Коэффициент отражения
· Коэффициент затухания
· Цвет поверхности
· Нормаль к поверхности (устанавливается после нахождения очередного пересечения).
|
|

Назначение каждого из этих классов дается в таблице 3.1:
Таблица 3.1
| Класс | Комментарии |
| CTexture | Реализует интерфейс обращения к любому типу текстуры в виде набора виртуальных функций, а также хранит указатель на объект класса файла текстуры |
| CTextureFile | Обеспечивает загрузку из файла битовой карты текстуры или генерацию процедурной текстуры, ее интерпретацию, а также предоставляет методы обращения к этой карте. |
| CParallelTexture | Класс текстуры, накладываемой на треугольник |
| CPerlinNoise | Класс генерирующий процедурную фактуру с помощью шума Перлина |
Назначение классов, реализующих текстуру и фактуру
3.2.3 Базовые трехмерные объекты
Все классы трехмерных объектов, с которыми находится пересечение лучей, наследуются от абстрактного класса C3DObject, который реализует такие операции, присущие всем объектам, как пространственные преобразования, а также предоставляет унифицированный интерфейс обращения к объектам через виртуальные функции (таким способом реализованы методы поиска пересечений, текстурирования, фактурирования).
Диаграмма классов выглядит следующим образом:
|
|

Подобная иерархия является необходимой в силу того, что для каждого типа трехмерного объекта реализуются свои алгоритмы поиска пересечений и определения нормалей к поверхности. Для унификации доступа к различным объектам выделено базовое понятие трехмерного объекта.
Необходимо заметить, что класс объекта содержит в себе не экземпляры текстуры и материала, а всего лишь указатели на них, что позволяет сэкономить память и вычислительные ресурсы, а также повторно использовать объекты вспомогательных классов в других трехмерных объектах.
3.2.4 Источник света
Источники света являются одними из основных понятий, участвующих в построении трехмерного изображения. В программе реализован только один источника – солнце, однако для возможности добавления новых источников света(Луны, фонарей) и большей гибкости программы был выделен класс-предок CLight, от которого наследуется класс солнечного источника света CSun.

На рис. 3.3 изображена соответствующая диаграмма классов.
Одним из ключевых механизмов базового алгоритма трассировки лучей является метод, который позволяет получить степень затенения. Он реализует тени от загораживающих источники света объектов.
Метод shadingCoef, реализующий этот механизм, объявлен как виртуальный в классе CLight и реализуется уже в классе CSun.
3.2.5 Сцена
Класс сцены SeaScene полностью характеризует набор объектов и их свойств, подлежащих визуализации. Он включает:

Объекты лодка, солнце и водная поверхность (экземпляры классов CBoat, CSun, CWater)
· Методы установки параметров камеры
· Методы параметров самих объектов
· Информация о размере строящегося изображения и субпиксельном разбиении
· Методы получения трассирующих лучей
Соответствующая диаграмма классов представлена на рис. 3.4.
3.2.6 Алгоритмы визуализации
Базовые алгоритмы визуализации представлены в классе CRender. Этот класс хранит указатель на объект класса SeaScene и все действия совершает над ним. Основные методы класса перечислены в таблице 3.2.
Таблица 3.2. Методы класса визуализации
| Метод | Комментарии |
| CRender(SeaScene *scene) | Конструктор класса, принимающий указатель на объект-сцену. Инициализирует объект визуализации. |
| renderFrame(int xr, int yr, int d, CPaintDC *dc) | Метод построения изображения, являющийся «оболочкой» для всех остальных методов. Включает цикл по пикселам изображаемого изображения, вычисление луча для каждого пиксела, вызов процедур реализации алгоритма и закраски пиксела полученным цветом. |
| trace(double refr, double att, CRay& ray, int level=0) | Метод, реализующий алгоритм обратной трассировки лучей. Здесь осуществляется поиск пересечений луча с объектами сцены и вызывается процедура определения цвета. |
| shade(double refr, double att, CRay& ray, C3DObject* obj, int level) | Метод определения цвета точки поверхности. Содержит реализацию формулы Уиттеда и вызов процедуры теневого луча каждого источника света. |
3.2.7 Классы интерфейса
Интерфейс данной программы строился путем создания классов диалоговых окон, меню и элементов управления, унаследованных от стандартных классов библиотеки MFC. Общая диаграмма классов интерфейса изображена на рис. 3.6.
3.3. Пользовательский интерфейс
Программа имеет русскоязычный интерфейс, организованный в виде главного меню и ряда диалоговых окон, позволяющих пользователю после старта программы устанавливать параметры как самих объектов сцены (лодка ,солнце водная поверхность), так положение и направление луча наблюдения камеры и размер получаемого изображения.
Доступ ко всем функциям и настройкам программы осуществляется через главное меню.
Структура главного меню:
– Настройки
· Разрешение – установка размеров получаемого изображения.
· Параметры – установка параметров сцены.
· Положение камеры – установка положения и ориентации камеры
– Построение
· Построение – прорисовка одиночного кадра сцены.
· Движение – циклическая прорисовка кадров при движении лодки
– Выход – завершение работы программы.
3.3.2 Диалог установки размера изображения
|

Внешний вид диалогового окна с установленными по умолчанию значениями показан на рис. 3.7.
|
|
3.3.3 Диалог
установки параметров сцены
Диалоговое окно параметров сцены

Рис. 3.8 Для задания параметров сцены используется диалог представленный на рис. 3.8, который содержит три вкладки: «Общие», «Лодка», «Вода». Они предназначены для задания общих параметров сцены, для задания параметров лодки, и для задания параметров водной поверхности соответственно.
На закладке «Общие», можно изменять дату и время и широту местности для изменения положения солнца, параметры ветра, фоновую освещенность и цвет неба.
Для задания параметров лодки используется вкладка «Лодка» (см. рис. 3.9)
Вкладка «Лодка»

Рис. 3.9 Кроме габаритных параметров, для лодки можно задавать цвет материала и цвет паруса, для этого нужно нажать кнопку «Выбрать» напротив соответствующей надписи – откроется стандартный диалог выбора цвета. Выбранный цвет отображается в прямоугольнике слева от кнопки.
Можно также выбрать текстуру, которая будет накладываться на лодку и парус, для этого нужно установить флажки «Текстура лодки» и «Текстура паруса» и выбрать файлы текстур в формате BMP.

Для редактирования свойств материала лодки используется диалоговое окно редактора материала, показанное на рис. 3.10.
Как можно видеть из рисунка, данное диалоговое окно позволяет устанавливать все параметры, указанные в классе CSurface.
|
Рис. 3.11 Для водной поверхности можно задать только ее цвет с помощью кнопки «Выбрать».
Для того, чтобы изменения вступили в силу, нужно нажать кнопку «ОК». Нажатие кнопки «Отмена» оставит все параметры такими, какими они были до изменения.
3.3.4 Диалог установки параметров камеры
Последним диалоговым окном, которое можно вызвать из редактора сцены, является окно установки параметров камеры, изображенное на рис. 3.12.
|

Из рисунка видно, что в диалоговом окне можно установить точку, в которой расположена камера, а также задать вектор, вдоль которого будет направлен луч наблюдения.
3.4 Условия применения программы
Минимальные требования к аппаратным средствам и программному обеспечению ЭВМ:
Операционная система MicrosoftWindows
Процессор IntelPentium 133 МГц;
Оперативная память 8 МБ;
SVGA-видеокарта, видеопамять 1 МБ;
1 МБ свободного места на диске .
3.5 Обращение к программе
Передача управления программе осуществляется посредством запуска исполняемого файла grapher.exe.
3.6 Входные и выходные данные
Входные данные: общие параметры объектов сцены.
Выходные данные: изображение сцены.
3.7 Сообщения
При редактировании параметров могут возникать следующие сообщения (см. табл. 3.7.):
Таблица 3.7 «Сообщение программы»
| Сообщение | Описание |
| «Пожалуйста введите число от A до B» | Требуется ввести действительное число из интервала [A;B] для заданного параметра. |
| «Пожалуйста, введите целое число от A до B» | Требуется ввести целое число из интервала [A;B] для заданного параметра. |
| «Пожалуйста, введите число» | Данный параметр может быть только числом. Сообщение возникает когда окно ввода не содержит знаков или содержит символы кроме цифр. |
4. ЭКСПЕРИМЕНТАЛЬНО-ИССЛЕДОВАТЕЛЬСКИЙ РАЗДЕЛ
4.1 Описание экспериментов
Для исследования временных характеристик алгоритма обратной трассировки лучей были проведены эксперименты по увеличению размера рассчитываемого изображения при следующих условиях:
· Без использования текстур
· С использованием текстур
Эксперименты проводились на компьютере IntelPentiumIII 566 МГц, 196 Мб ОП, графическая карта 3dfxVodoo3 4 Мб.
4.2. Результаты экспериментов
|

Из полученного графика, изображенного на рис. 4.1, можно заметить:
· С ростом количества пикселей вычислительные затраты возрастают линейно, что имеет большое значение при построении изображений больших размеров.
· Текстурирование и фактурирование требуют весьма небольших затрат времени.
5. ЗАКЛЮЧЕНИЕ
Разработанная программа позволяет получать на экране растрового дисплея реалистическое изображение трехмерной сцены моря с лодкой и учитывать различные природные явления как ветер, блики на воде, благодаря алгоритму обратной трассировки лучей и глобальной модели освещения Уиттеда. Также были разработаны алгоритмы для решения частных задач: определение положения солнца в зависимости от даты и времени наблюдения и широты местности, расчет неровностей водной поверхности с помощью шума Перлина. Программа полностью удовлетворяет требованиям технического задания, обеспечивая:
· Возможность задания сцены с различными размерами и положением лодки, положением солнца и освещенностью, а также произвольно задавать расположение и направление луча камеры.
· Поддержку наложения на трехмерные объекты текстуры и фактуры.
· Улучшение качества изображения с использованием алгоритма стохастического суперсэмплинга.
· Русскоязычный интерфейс пользователя.
По результатам работы программы были сделаны выводы:
· Алгоритм обратной трассировки лучей обеспечивает высокую степень реалистичности изображения, однако скорость выполнения вычислений на однопроцессорных системах оставляет желать лучшего. Тем не менее, скорее всего, данный алгоритм будет широко использоваться на параллельных вычислительных машинах, таких как кластеры, а также MISD- и MIMD-машинах.
· Без дополнительной оптимизации увеличение размера изображения ведет к значительному увеличению времени построения.
· Алгоритм моделирования водной поверхности с помощью фактурирования шумом Перлина показал реалистичность изображения воды при достаточно низких вычислительных затратах.
В качестве дальнейшего развития комплекса предполагается сделать шумовую функцию трехмерной для улучшения динамичности воды, а также оптимизацию программы для большого количества примитивов и разбиение водной поверхности на треугольники с помощью сетки высот.
6. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Роджерс Д. Алгоритмические основы машинной графики / Пер. с англ. –М.:Мир, 1989. – 512 с.,ил.
2. Авдеева С.М., Куров А.В. Алгоритмы трехмерной машинной графики: учебное пособие. – М.: Издательство МГТУ им. Н.Э.Баумана, 1996. – 60 с., ил.
3. Шикин Е.В., Боресков А.В. Компьютерная графика. Динамика, реалистические изображения. – М.: Диалог-МИФИ, 1995. – 288 с.
4. Prosise, Jeff. Programming Windows with MFC – 2nd ed. – Washington - Microsoft Press,1999. – 112 с., ил.
5. Страуструп Б. Язык программирования C++, спец. изд. / Пер. с англ. – М.: СПб.: Издательство Бином – Невский Диалект, 2002. – 1099 с., ил.
6. Воронцов-Вельяминов Б.А. Очерки о Вселенной.-М.: Наука, 1964.- 552с., ил.
7. Watt, Mark. Ligth-Water Interaction using Backward Beam Tracing // Computer Graphics, Volume 24, Number 4, August 1990 – London, Digital Pictures, 1990 – 23-32
8. Борн М., Вольф Э. Основы оптики.- М.: Наука, 1970, 885 с.
9. Hugo Elias. Perlin Noise // СайтVirgin.net ISP:
URL: http://freespace.virgin.net/hugo.elias/models/m_perlin.htm
Обозначения, использованные в диаграммах классов:
Класс:

Наследование класса B от класса A:

Агрегация классом А одного экземпляра класса В:

Включение классом А экземпляра класса В по указателю или ссылке:
