| Скачать .docx |
Курсовая работа: Дослідження зміни швидкості та витікання ідеального газу із ємкості під тиском
Курсова робота
на тему: «Дослідження зміни швидкості та витікання ідеального газу із ємкості під тиском»
Постановка задачі
Описати масив структур з трьох елементів. Кожна структура об’єднує дані для одного варіанта розрахунків. Необхідно для кожного варіанта на відрізку часу від 0 до Т з кроком dt (∆ t) побудувати графік зміни швидкості та витікання ідеального газу із ємкості під тиском.
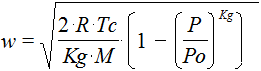
Де R – універсальна газова стала, M – молекулярна маса газу, Tc – температура в ємкості, Po – тиск у ємкості.
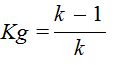 де
де 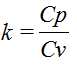 – відношення теплоємностей.
– відношення теплоємностей.
Температура Ро та То змінюється в часі:
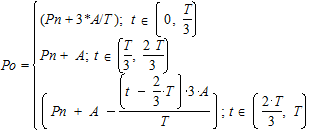
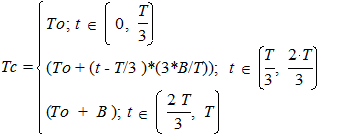
Тут Рn, A, To, B – задані константи. Вхідні дані зчитувати з файлу, результати розрахунків записувати в інший файл. Передбачити окремі функції для обчислення Ро та То.
Нижче представлені 3 варіанти вхідних даних:
1) R = 8.31696 Дж/грам*моль, To = 400о К, час T = 1200 с, dt = 600 с, B = 50 о К, Pn = 3.2, A = 1.2, M = 28.96, K = 1.402, P = 1.2 атм.
2) R = 8.31696 Дж/грам*моль, To = 400о К, час T = 1200 с, dt = 600 с, B = 50 о К, Pn = 4, A = 1.5, M = 28.96, K = 1.402, P = 1.5 атм.
3) R = 8.31696 Дж/грам*моль, To = 400о К, час T = 1200 с, dt = 600 с, B = 50 о К, Pn = 5, A = 2, M = 28.96, K = 1.402, P = 2 атм.
Таблиця символічних імен
| Змінна |
Фізичний зміст |
Одиниця вимірювання |
| R |
універсальна газова стала |
Дж/грам*моль (Дж – Джоуль) |
| T |
час за який газ витікає із ємкості |
с (секунди) |
| dt |
крок що береться для оцінки зміни стану газу у часі |
_ |
| B |
задана константа |
_ |
| M |
молекулярна маса газу |
|
| Тс |
температура в ємкості |
°К (градусів за Кельвіном) |
| Ро |
тиск у ємкості |
Па (Паскаль) |
| Pn |
задана константа |
_ |
| A |
задана константа |
_ |
| To |
задана константа |
_ |
| p |
тиск що діє на газ у ємкості |
атм. |
| t |
час |
с (секунди) |
| Kg |
Kg = (k‑1)/k |
_ |
| k |
відношення теплоємкостей |
_ |
Блок – схема
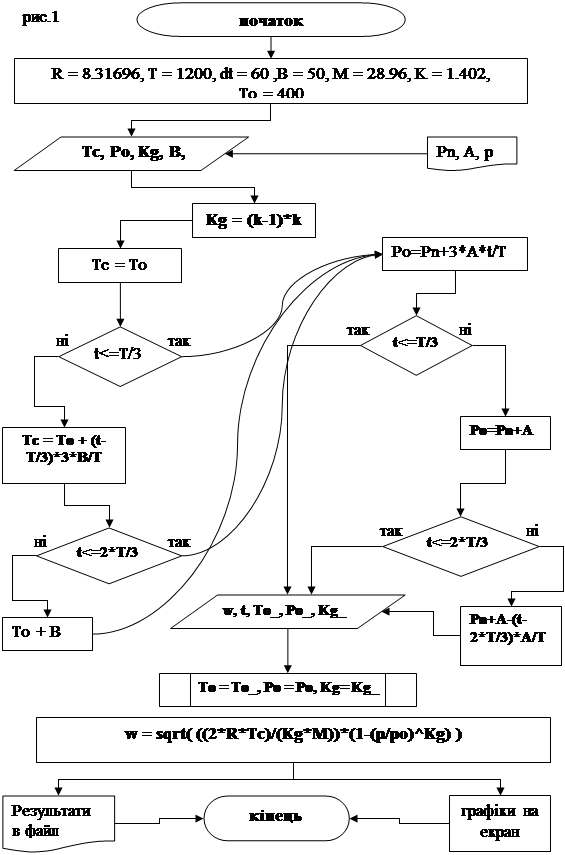
Текст програми мовою С
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <conio.h>
#include <graphics.h>
#define №3
#define FN 21
#define R_ 8.31696
#define T_ 1200
#define dt_ 60
#define B_ 50
#define M_ 28.96
#define K_ 1.402
#define T0_ 400
struct data
{
float Pn;
float A;
float p;
}
x[N];
float Tc (float T0, float B, float t, float T);
float P0 (float Pn, float A, float t, float T);
float Kg (float K);
void graf_output (int c, float xu[], float yv[], int N_, char*title);
// –
void main()
{
float tx[N] [FN];
float wx[N] [FN];
float w, t, Tc_, P0_, Kg_;
int i, j;
char str[40];
FILE *data;
FILE *out;
clrscr();
data = fopen («input.txt», «r»);
if (! data)
{
printf («The file input.txt hasn't been found. Please create it or change the directory. \n»);
getch();
exit(1);
}
out = fopen («output.txt», «w»);
for (i=0; i<N; i++)
{
fscanf (data, «%f % f % f»,&x[i].Pn,&x[i].A,&x[i].p);
}
printf («Please type in any decimal number:»);
scanf («%f»,&Kg_);
fclose(data);
clrscr();
for (i=0; i<N; i++)
{
for (t=0, j=0; t<=T_; t=t+dt_, j++)
{
Tc_ = Tc (T0_, B_, t, T_);
P0_ = P0 (x[i].Pn, x[i].A, t, T_);
Kg_ = Kg (K_);
w = 2*R_*Tc_/(Kg_ * M_);
w *= 1 – pow (x[i].p/P0_, Kg_);
w = sqrt(w);
fprintf (out, «%.0f\t%.5f\n», t, w);
tx[i] [j]=t;
wx[i] [j]=w;
}
fprintf (out, "\n\n\n\n»);
}
fclose(out);
printf («All the function values (values of graph points' coordinates) will be put into \nthe output.txt file.\n»);
printf («You are able to change the values of Pn, A and p. Change those\nvalues in the input.txt file.\n»);
printf («The correct order of typing the values is showed under the graphs\n\n\n\n»);
printf («Press Enter to continue»);
getch();
for (i=0; i<N; i++)
{
sprintf (str, «Ph =%.3f, A =%.3f, P =%.3 f.», x[i].Pn, x[i].A, x[i].p);
graf_output (i, tx[i], wx[i], FN, str);
fflush(stdin);
getch();
}
}
// –
void graf_output (int c, float xu[], float yv[], int N_, char*title)
{
int gdriver = DETECT, gmode, errorcode;
int xmax, ymax; // the maximum coordiantes x(width) y(hight)
int xmin, ymin; // spaces between the graph and screen adges
int x, y; // current coordinates
int x_, y_; // previous coordinates
int i;
char st[20];
double miny, maxy; // extreem values of y
initgraph (&gdriver, &gmode, «e:\\turbocpp\\bgi»);
xmin = 90;
ymin = 100;
xmax = getmaxx() – 20;
ymax = getmaxy() – 40;
maxy = miny = yv[0];
for (i=0; i<N_; i++)
{
miny = (yv[i]<miny)? yv[i]:miny;
maxy = (yv[i]>maxy)? yv[i]:maxy;
}
rectangle (0,0, getmaxx(), getmaxy());
setbkcolor(7);
sprintf (st, «Input variant number % d», c+1);
outtextxy (10,3, st);
outtextxy (10,30, title);
// first 2 lines-the axises x and y. next we got the pointers building (y>, x>)
line (xmin, ymin, xmin, ymax);
line (xmin, ymax, xmax, ymax);
line (xmin, ymin, xmin+3, ymin+5);
line (xmin, ymin, xmin‑3, ymin+5);
line (xmax, ymax, xmax‑5, ymax‑3);
line (xmax, ymax, xmax‑5, ymax+3);
setcolor(1);
outtextxy (xmin+6, ymin, «w»);
outtextxy (xmax, ymax+15, «t»);
for (y=ymax‑20; y>ymin+10; y-= 20)
{
//we got points | painted and the numbers on the exis Oy
setcolor(14);
line (xmin‑2, y, xmin+2, y);
sprintf (st, «%0.5lf», maxy – (y-ymin)*(maxy – miny)/(ymax – ymin));
outtextxy (xmin‑70, y‑3, st);
}
x_ = xmin;
y_ = ymax;
for (i=0; i<N_; i++)
{
x = xmin + ((xu[i] – xu[0])*(xmax – xmin)/(xu [N_-1] – xu[0]));
y =(int) ((yv[i] – miny)*(ymax – ymin)/(maxy – miny));
y = ymax – y;
//we got points | painted and the numbers on the exis Ox
setcolor(14);
line (x, ymax‑2, x, ymax+2);
if (i % 4==0)
{
sprintf (st, «%0.2lf», xu[i]);
outtextxy (x‑10, ymax + 4, st);
}
// let's set the rad color to the «graph line»
setcolor(4);
line (x_, y_, x, y);
x_ = x;
y_ = y;
}
}
// –
float Tc (float T0, float B, float t, float T) {
if (t<=(T/3)) return T0;
if (t<=(2*T/3)) return T0 + (t – T/3)*3*B/T;
return T0 + B;
}
float P0 (float Pn, float A, float t, float T) {
if (t<=(T/3)) return Pn + 3*A*t/T;
if (t<=(2*T/3)) return Pn + A;
return Pn + A – (t – 2*T/3) * 3 * A / T;
}
float Kg (float K) {
return (K – 1)/K;
}
Результати роботи програми
Виведення даних на екран
Виведення даних у файл
0 14.01538
60 14.34739
120 14.65061
180 14.92912
240 15.18624
300 15.42468
360 15.64668
420 15.83574
480 15.98260
540 16.12811
600 16.27233
660 16.41529
720 16.55700
780 16.69752
840 16.59581
900 16.36035
960 16.10744
1020 15.83472
1080 15.53932
1140 15.21771
1200 14.86556
0 14.01538
60 14.34739
120 14.65061
180 14.92912
240 15.18624
300 15.42468
360 15.64668
420 15.83574
480 15.98260
540 16.12811
600 16.27233
660 16.41529
720 16.55700
780 16.69752
840 16.59581
900 16.36035
960 16.10744
1020 15.83472
1080 15.53932
1140 15.21771
1200 14.86556
0 13.60640
60 13.97651
120 14.31201
180 14.61820
240 14.89929
300 15.15864
360 15.39904
420 15.59843
480 15.74309
540 15.88643
600 16.02849
660 16.16930
720 16.30889
780 16.44730
840 16.33315
900 16.07817
960 15.80308
1020 15.50495
1080 15.18018
1140 14.82432
1200 14.43177
Висновок
В результаті виконання курсової роботи був створений алгоритм і комп’ютерна програма для побудови графіків зміни швидкості та витікання ідеального газу із ємкості під тиском на певному відрізку часу. З файлу були зчитані декілька варіантів вхідних даних, результати обчислень записані в файл. При аналізі побудованих графіків робимо висновок про взаємозалежність між заданими фізичними величинами та константами.
Використана література
1. Дистанційний курс «Алгоритмічні мови» Авраменко В.В. http://dl.sumdu.edu.ua
2. Б.В. Керниган, Д.М. Ричи «Язык программирования С»
3. Р. Уинер «Язик Turbo C»