Курсовая работа: Реализация звуковых эффектов

Министерство Образования и Науки Украины

Курсовой проект на тему:

«РЕАЛИЗАЦИЯ ЗВУКОВЫХ МУЗЫКАЛЬНЫХ ЭФФЕКТОВ»

по курсу «Системы обработки мультимедийных данных»

2006

Содержание

ВВЕДЕНИЕ

1 ПОСТАНОВКА ЗАДАЧИ

2 ОБЗОР СУЩЕСТВУЮЩИХ СИСТЕМ И МЕТОДОВ РЕАЛИЗАЦИИ ЗВУКОВЫХ ЭФФЕКТОВ

3 МЕТОДЫ РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ

3.1 Эффекты, основанные на задержке сигнала.

3.1.1 – Простые звуковые эффекты

3.1.2 – Более сложные звуковые эффекты

4 РАЗРАБОТКА ПРОГРАММНОЙ МОДЕЛИ НА MATLAB

5 РАЗРАБОТКА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СИСТЕМЫ НА ЯЗЫКЕ СИ

6 РЕЗУЛЬТАТЫ РЕАЛИЗАЦИИ ЗВУКОВЫХ ЭФФЕКТОВ В СРЕДЕ MATLAB И НА СИГНАЛЬНОМ ПРОЦЕССОРЕ DSP

7 КРАТКОЕ РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ

ЗАКЛЮЧЕНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ПРИЛОЖЕНИЕ А

ПРИЛОЖЕНИЕ Б

ПРИЛОЖЕНИЕ В

Введение

В современной музыкальной индустрии повсеместно используются различные звуковые эффекты, обогащающие палитру музыкальных произведений и добавляющие к ним дополнительные краски. Эффекты могут использоваться не только при обработке музыкальных произведений, но и при воспроизведении речевого материала для снижения монотонности при прослушивании длительных фрагментов.

Обработать звук на высоком уровне можно программным способом. Существует множество различных звуковых редакторов, позволяющих делать со звуком значительно более сложные вещи, чем это позволяют делать даже самые сложные эффект-процессоры. Кроме того, эффект-процессоры часто эмулируются в виртуальных WT-синтезаторах, а также находят программную реализацию в специальных программах для обработки звука в режиме реального времени.

Аппаратную реализацию звуковые эффекты находят в цифровых сигнальных процессорах (DSP). Любой MIDI-синтезатор имеет встроенный эффект-процессор той или иной сложности (эффект-процессор представляет собой один или несколько DSP). Сложные эффект-процессоры "умеют" накладывать на звуковой сигнал сразу несколько различных эффектов, причем, отдельно для каждого канала, позволяя регулировать параметры эффектов в режиме реального времени. Однако стоимость таких эффект-процессоров чрезвычайно высока (как и стоимость любого другого высокопроизводительного микропроцессора), поэтому профессиональные DSP устанавливаются только на качественной музыкальной аппаратуре. На более или менее дешевых звуковых платах часто устанавливается DSP с упрощенным набором возможностей: наложение одного или нескольких эффектов на все каналы одновременно.

В курсовой работе предусмотрена обработка музыкальных файлов как программно – на языке Matlab, так и аппаратно – на цифровом сигнальном процессоре с помощью программы CodeComposerStudio (CCS).

1 Постановка задачи

В данной курсовой работе необходимо разработать в среде Matlab, а также на ЦПОС TMS320C6711(5402) систему, реализующую звуковые музыкальные эффекты. Необходимо реализовать эффекты: однократной и многократной цифровой задержки, эффект детонации, эффект хора, эффект вибрато, компрессор и экспандер. Входные данные должны вводиться из монофонического звукового файла формата «wav» (частота дискретизации – 8кГц, разрядность - 16 бит).

2 Обзор существующих систем и методов реализации звуковых эффектов

Все преобразования звука сводятся к нижеследующим.

Амплитудные преобразования. Выполняются над амплитудой сигнала. Такую процедуру можно проделать двумя способами: либо умножая амплитуду сигнала на некоторое фиксированное число, в результате чего получится одинаковое изменение интенсивности сигнала на всей его протяженности, то есть усиление или ослабление, либо изменяя амплитуду сигнала по какому-то закону, то есть умножая амплитуду сигнала на модулирующую функцию. Последний процесс называется амплитудной модуляцией.

Спектральные (частотные) преобразования. Такие преобразования выполняются над частотными составляющими звука. Фактически сигнал представляется рядом Фурье, то есть раскладывается на простейшие синусоидальные колебания различных частот и амплитуд. Затем производится обработка необходимых частотных составляющих (например, фильтрация) и обратная свертка. В отличие от амплитудных преобразований, эта процедура значительно более сложная в исполнении, так как сам процесс разложения звука на простейшие синусоидальные колебания очень трудоемок.

Фазовые преобразования. Выполняются либо путем постоянного сдвига фазы сигнала, либо путем наложения некоторой фазомодулирующей функции. Такие преобразования, например, стерео сигнала, позволяют реализовать эффект вращения или "объёмности" звука.

Временные преобразования. Реализуются путем наложения на сигнал одной или нескольких его копий, сдвинутых во времени. Позволяют создать эффекты эха или хора. Кроме того, временные преобразования могут влиять на пространственные характеристики звука.

Формантные преобразования. Выполняются над формантами - усиленными участками спектра звука. Применительно к звуку, сформированному речевым аппаратом человека, изменяя параметры формант, фактически можно изменять восприятие тембра и высоты голоса.

Фильтрация звука. К фильтрации прибегают в случаях, когда необходимо ограничить или изменить спектр звукового сигнала в каком-то определенном частотном диапазоне. Путем фильтрации звука, можно избавиться, например, от нежелательных шумов или помех, подавить определенные частотные полосы. Существует и еще один немаловажный аспект применения фильтрации. Часто устройства, с помощью которых производится запись и преобразования звуковых сигналов, имеют нелинейную зависимость амплитуды от частоты сигнала. Это означает, что при записи одни частотные составляющие звука могут быть завышены, а другие занижены. Фильтрация позволяет нормализовать частотные составляющие в необходимом диапазоне.

Таким образом, фильтрацию сигналов можно в целом классифицировать следующим образом:

- фильтрация, в результате которой происходит усиление или ослабление отдельных частотных составляющих спектра;

- полное подавление частотных составляющих в определенной полосе частот.

Фильтрация реализуется с помощью различных устройств и алгоритмов. Одним из наиболее известных фильтрующих устройств является эквалайзер. Эквалайзер позволяет регулировать (усиливать или ослаблять) уровень частотных составляющих в определенной полосе частот, тем самым фактически регулируя тембр звука. Применительно к компьютерной технике, аппаратная реализация фильтрующих устройств в достаточной степени затруднена, так как процесс фильтрации предполагает разложение сигнала в ряд Фурье, что является математически трудоемкой операцией. Однако реализацию фильтров той или иной сложности можно найти в цифровых сигнальных процессорах (DSP - Digital Signal Processor), используемых в профессиональной и полупрофессиональной музыкальной аппаратуре (хотя в последнее время это утверждение стало частично относиться также и к бытовым звуковым устройствам). Фильтрация находит реализацию и в различном программном обеспечении, предназначенном для обработки звука. В таком случае процессы фильтрации чаще всего происходят не в реальном времени.

3 методы решения поставленной задачи

В данном курсовом проекте реализованы методы, основанные на использовании задержки, а также основанные на частотном преобразовании. Рассмотрим подробнее данные методы.

3.1 Однократная задержка сигнала

Одним из самых распространенных классов являются звуковые эффекты, основанные на задержке сигнала. В реальной ситуации задержка звукового сигнала может возникнуть при отражении звуковой волны от твердой преграды, например, от стены. Величину возникающей при этом задержки легко определить, зная пройденный звуковой волной путь и учитывая, что скорость звука на уровне моря можно считать равной 330 м/с. Таким образом, за одну миллисекунду звуковая волна проходит 33 сантиметра. Для расчетов удобнее помнить, что один метр она проходит за 3 мс.

Рассмотрим сначала реализацию однократного отражения звуковой волны. Этот простой эффект является базовым для реализации более сложных эффектов, таких, как имитация реверберации и хора.

Как уже говорилось выше, отражение звуковой волны от твердой преграды приводит к появлению в точке регистрации задержанной версии излучаемого сигнала. До появления цифровых процессоров обработки сигнала и других цифровых устройств для задержки основного сигнала использовались специальные магнитофоны с несколькими подвижными головками. При цифровой реализации линии задержки входной аналоговый сигнал преобразуется в цифровую форму, записывается в циклический или любой другой буфер задержки, и сигнал с выхода этого буфера задержки преобразуется обратно в аналоговую форму и воспроизводится.

Блок-схема реализации однократной задержки звукового сигнала приведена на рисунке 3.1.1

Рисунок 3.1.1 - Блок-схема реализации однократной задержки звукового сигнала

Входной сигнал х(п) одновременно поступает на линию задержки и на сумматор, формирующий выходной сигнал. Задержанный на величину D сигнал х(п) умножается на масштабный коэффициент а и также поступает на сумматор, формирующий выходной сигнал. Преобразования, осуществляемые данной схемой, могут быть выражены следующей формулой:

. (3.1.1)

Данная схема является линейным фильтром с передаточной функцией:

. (3.1.2)

Поскольку при любом отражении звуковой сигнал ослабляется, то -1 < а < 1. Отрицательные значения соответствуют отражению в противофазе. Эта модель является достаточно грубой, поскольку как распространение звуковой волны, так и ее отражение являются частотно-зависимыми процессами. Однако в большинстве случаев эта модель является адекватной. Величина D определяется разностью времени между приходом прямой и отраженной звуковой волны.

Передаточная характеристика (3.1.2) является характеристикой гребенчатого фильтра. Отличительной особенностью данного класса фильтров является выполнение для них равенства

^. (3.1.3)

Однократная цифровая задержка часто используется для оживления "сухой" музыки. В этом случае как основной, так и задержанный аудиосигналы складываются с одинаковой амплитудой. Для того чтобы при выполнении этой операции не возникало переполнения разрядной сетки цифрового устройства, оба сигнала складываются с коэффициентом 1/2. В этом случае используется задержка порядка 15—40 мс. Введение этой задержки приводит к появлению у слушателя впечатления, что два исполнителя играют в унисон. При уменьшении величины задержки ниже 10 мс в сигнале могут возникнуть нежелательные биения, поскольку сумма двух гармонических сигналов с одинаковой амплитудой может быть представлена как амплитудная модуляция гармонического сигнала с частотой, равной сумме частот исходных сигналов, гармоническим сигналом с частотой, равной разности частот исходных сигналов.

Область использования однократных задержек сигнала очень ограничена, поскольку в реальной жизни редко встречается ситуация, когда в акустическом поле присутствует только одна отражающая поверхность. Кроме того, как отмечалось выше, даже в этом случае для повышения адекватности модели необходимо использовать формирующий фильтр, учитывающий частотную характеристику отражающей поверхности и, возможно, частотную характеристику среды распространения сигнала. Для моделирования акустических полей с несколькими отражающими поверхностями и учета частотных характеристик процессов отражения и распространения звуковой волны используются многократные задержки.

3.2 Многократная задержка сигнала

Многократная задержка сигнала может быть достигнута двумя путями: доступом к различным элементам, хранящимся в одной линии задержки, или созданием нескольких отдельных линий, имеющих различное время задержки. Первый способ используется в цифровой обработке сигналов и в магнитофонах с несколькими считывающими головками, а второй — при использовании механических и электрических линий задержки.

Многократная задержка сигнала может быть реализована как с использованием трансверсальных (с конечной импульсной характеристикой), так и с использованием рекурсивных фильтров (с бесконечной импульсной характеристикой).

3.2.1 Многократная задержка с использованием трансверсального фильтра

Блок-схема реализации многократной задержки сигнала с использованием трансверсального фильтра приведена на рисунке 3.1.1.2.

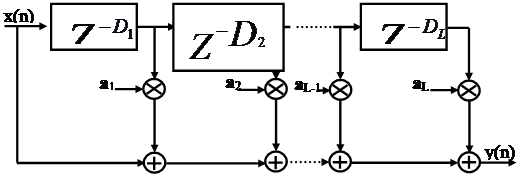
Рисунок 3.2.1.1 - Блок-схема реализации многократной задержки с использованием трансверсального фильтра

Разностное уравнение трансверсального фильтра может быть записано в виде:

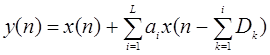(3.2.1.1)

В данном фильтре используются различные величины задержек входного сигнала, что не позволяет считать этот фильтр гребенчатым. Использование конечного числа линий задержки дает возможность учесть влияние ограниченного числа отражающих поверхностей.

Поскольку в трансверсальном фильтре может быть учтено только ограниченное число отражений сигнала, то его нельзя использовать для моделирования переотражений звуковой волны. Для этого следует использовать рекурсивные фильтры.

3.2.2 Многократная задержка с использованием рекурсивного фильтра

Блок-схема реализации многократной задержки с использованием простейшего рекурсивного фильтра приведена на рисунке 3.2.1.2.

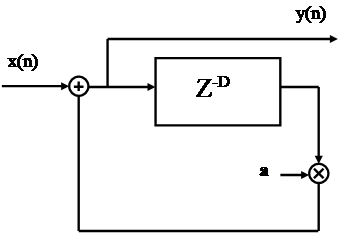Рисунок 3.2.2.1 – Блок-схема реализации многократной задержки с использованием рекурсивного фильтра

Этот фильтр может быть использован для описания переотражений звуковой волны между двумя бесконечными параллельными стенами, на одной из которых расположен излучатель плоской волны. Приемник может располагаться на любой из стен. При отражении от стены энергия звуковой волны падает в а раз. Импульсная характеристика данного фильтра представляет собой последовательность одиночных импульсов, расположенных па расстоянии D отсчетов друг от друга, причем импульс с номером п имеет амплитуду aⁿ .

Данный фильтр описывается разностным уравнением:

(3.2.2.1)

и имеет передаточную функцию:

(3.2.2.2)

Более сложные звуковые эффекты

Кроме описанных выше простейших звуковых эффектов существуют и более сложные, основанные на перемещении спектральных составляющих исходного сигнала. Такой эффект может быть, например, достигнут при изменении величины задержки сигнала по определенному закону в базовой блок-схеме, приведенной на рис.3.1.2.1

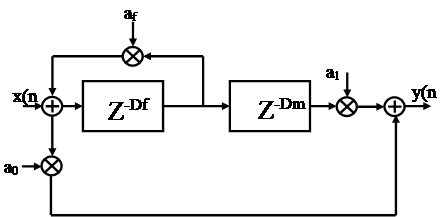
Рисунок - Базовая блок-схема

В этой блок-схеме величина D_f является постоянной, а величина D_т = f_m (t) представляет собой некоторую функцию времени. Поэтому данная блок-схема реализует гребенчатый фильтр с изменяющейся во времени частотной характеристикой. Эта блок-схема имеет слишком сложную структуру, чтобы описать ее одним разностным уравнением. Выбор закона изменения величины D_m , а также значения постоянных величин a₀ , a₁ , a_f и D_f позволяют реализовать различные эффекты.

3.3 Эффект детонации

Эффект детонации был открыт при попытке использования выходных сигналов с двух катушечных магнитофонов для создания эффекта хора, который будет описан ниже. В результате возник эффект, напоминающий звук взлетающего реактивного самолета.

Рисунок 3.3.1- Блок-схема устройства, реализующего эффект детонации

Для реализации эффекта детонации в цифровых устройствах может быть использовано устройство, блок-схема которого приведена на рисунке 3.3.1.

Как видно из рисунка 3.3.1, эта блок-схема является частным случаем базовой блок-схемы, изображенной на рисунке 3.3.1. Данной блок-схеме соответствует следующее разностное уравнение:

, (3.3.1)

где

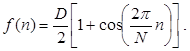
Для предотвращения возникновения переполнений разрядной сетки при вычислении выходного значения коэффициент а₀ выбирается равным 0,5, а коэффициент а₁ выбирается от -0,5 до 0,5. Значение параметра D, определяющего диапазон изменения задержки, обычно выбирается от 0.25 до 25 мс. Значение параметра N, определяющего частоту детонации, выбирается исходя из требований, предъявляемых к выходному сигналу.

Уменьшение длины линии задержки приводит к пропорциональному подъему частот спектральных составляющих исходного сигнала, а ее уменьшение — к понижению этих частот.

3.4 Эффект хора

Другим эффектом, обогащающим звуковую палитру произведения, является эффект хора. Он позволяет создать у слушателя иллюзию, что данное произведение одновременно исполняется на нескольких одинаковых музыкальных инструментах. Хотя музыканты стараются играть синхронно, они не могут избежать небольших отклонений от общего темпа. Кроме того, неизбежны различия в настройке отдельных инструментов и в громкости исполнения.

Для создания эффекта одновременного исполнения произведения на M инструментах может быть использовано устройство, блок-схема которого приведена на рисунке 3.4.1.

Как правило, все коэффициенты при реализации эффекта задержки выбираются равными (1/M), а сами величины задержки не превышают 15—35 мс. Естественно, что каждая линия задержки должна изменять свои параметры независимо от всех остальных.

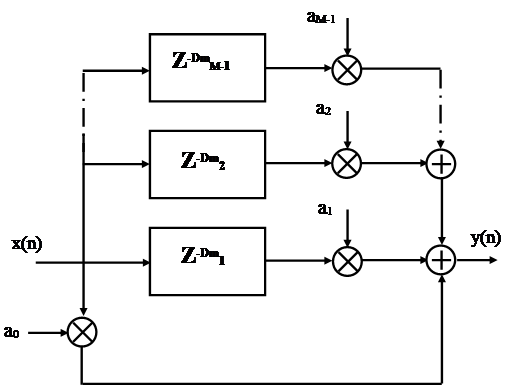
Рисунок 3.4.1 - Блок-схема устройства, реализующего эффект хора

При таком выборе коэффициентов моделируются только различия в темпе исполнения произведения и в настройке инструментов. То что эти различия связаны друг с другом, на слух не определяется, поскольку в реальной ситуации такая зависимость отсутствует, и слух не приспособлен для ее выделения. Для моделирования различного уровня воспроизведения достаточно сделать переменными коэффициенты фильтра, добавив к их постоянному значению некоторый случайный низкочастотный сигнал малого уровня, поскольку исполнители стараются сохранять средний уровень громкости при воспроизведении. Для простоты в качестве случайного низкочастотного сигнала может быть использован тот же самый сигнал, что и в линиях задержки.

Данной блок-схеме соответствует следующее разностное уравнение:

, (3.3.1)

где

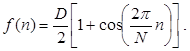
3.5 Эффект вибрато

Эффект вибрато имитирует вибрато человеческих голосов, определяющий их тембр, теплоту и выразительность, и соответствующий прием исполнения на струнных музыкальных инструментах, периодически изменяющий в небольших пределах высоту звуков. Эффект вибрато может быть получен в устройствах, реализующих эффекты детонации и хора при полном удалении входного сигнала из выходного. Величина задержки при этом выбирается таким образом, чтобы частотный сдвиг основных спектральных составляющих сигнала составлял несколько герц. Этот эффект часто путают с эффектом тремоло, где сигнал подвергается не частотной, а амплитудной модуляции. Оба эффекта используют одинаковый модулирующий сигнал. Эффекты тремоло и вибрато могут совместно использоваться для создания эффекта вращающегося диктора.

Блок-схема устройства, реализующего эффект вибрато, приведена на рисунке 3.5.1:

Рисунок 3.5.1 - Блок-схема устройства, реализующего эффект вибрато

Устройство, блок-схема которого приведена на рисунке 3.1.2.3.1, может использоваться также и для изменения основного тона диктора (например, чтобы сделать голос говорящего неузнаваемым). В этом случае величина задержки изменяется от нуля до некоторой предельной величины по линейному закону. По достижении задержки своей предельной величины она сбрасывается в ноль, и процесс возобновляется. Изменение задержки по такому закону позволяет обеспечить работу устройства в реальном времени, но в момент обнуления величины задержки слышен щелчок. Дело в том, что как раз в данный момент происходит разрыв воспроизводимого сигнала при переходе к повторному воспроизведению некоторого его участка.

Если необходимо не повысить, а понизить частоту основного тона, то величина задержки постоянно уменьшается и при достижении нуля устанавливается в свое максимальное значение. При таком переходе теряется часть входного сигнала. Для устранения щелчков, возникающих при изменении величины задержки, рекомендуется использовать фильтры нижних частот.

Более простым способом устранения щелчков является использование двух подобных устройств, фазы пилообразных модулирующих сигналов которых сдвинуты на половину периода. При этом необходимо задать весовое окно (например, окно Ханна) на периоде модулирующего сигнала. Выходные сигналы каждого устройства умножаются на отсчет весовой функции, соответствующий текущей длине линии задержки, и складываются друг с другом, что обеспечивает устранение щелчков при переходах. Если обозначить период модулирующего сигнала как N, отсчет модулирующего сигнала как f_т (п), а отсчет весовой функции как W(п), то, с использованием функции получения остатка от целочисленного деления числа M на число N, обозначаемой как mod_N (М), процедура преобразования основного тона может быть записана в форме следующего разностного уравнения:

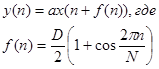(3.5.1)

3.6 Изменение динамического диапазона: компрессоры и экспандеры

Компрессоры и экспандеры используются для изменения динамического диапазона сигнала, т. е. для уменьшения различия уровней самого тихого и самого громкого сигналов. Для этого при превышении текущим значением сигнала некоторого порога устанавливается коэффициент передачи, меньший, чем используемый до превышения порога. Отношение старого коэффициента передачи к новому называется ослаблением. Все коэффициенты передачи задаются в логарифмической шкале. То есть при ослаблении 2:1 приращению входного сигнала на 20 дБ будет соответствовать приращение выходного сигнала на 10 дБ. Подобный компрессор, изменяющий свою передаточную характеристику в точке а, может быть реализован по следующей формуле:

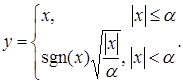(3.6.1)

Применение компрессоров позволяет передавать по линиям связи сигналы, имеющие больший динамический диапазон, чем передающий канал. На приемном конце этой линии устанавливается экспандер, имеющий передаточную характеристику, обратную характеристике компрессора.

Другой областью применения компрессоров является звукозаписывающая индустрия и радиовещание. Дело в том, что при записи музыкальных произведений для более точной передачи звучания всех групп инструментов оркестра устанавливается несколько микрофонов. Звуковое давление создает на выходе микрофона электрический сигнал, имеющий динамической диапазон 60—70 дБ. Однако большинство каналов неспособно передать весь диапазон изменения сигнала вследствие ограничений, накладываемых помехами в канале и его нелинейностями. Поэтому возникает задача сжать исходный динамический диапазон сигнала до динамического диапазона канала, обычно составляющего порядка 40 дБ.

При уровне ослабления выше, чем 10:1, компрессор превращается в ограничитель. Его основное отличие заключается в том, что применение компрессора предполагает последующее использование экспандера, а после ограничителя какие-либо разговоры о восстановлении сигнала, как правило, бессмысленны. Поэтому наиболее часто используются ограничители с уровнем ослабления ¥ : 1, что соответствует ограничению сигнала на уровне порога.

Поскольку передаточные характеристики компрессоров и экспандеров отличаются большой нелинейностью, их использование приводит к существенному искажению сигнала. Так, например, при использовании аналоговых компрессоров и экспандеров неизбежно возникает вопрос об обеспечении равенства амплитуд передаваемого и принимаемого сигналов, поскольку в противном случае точки изменения коэффициентов передачи компрессора и экспандера не совпадут, что приведет к возникновению нелинейных искажений. Как отмечалось выше, во многих случаях необходимо производить компрессию сигнала с опережением, т.е. до фактического превышения сигналом порогового уровня. В этом случае при медленном росте или спаде сигнала несоответствие точек изменения коэффициентов передачи приведет к растягиванию во времени описанных выше нелинейных искажений.

4 Разработка программной модели на MATLAB

В данной работе использовалась программная среда MatLab, в которой и были реализованы необходимые звуковые эффекты. Для синтеза звуковых эффектов использовались разностные уравнения фильтров, приведенные в предыдущем разделе.

Программная реализация обработки звуковых сигналов приведена в приложении А.

5 Разработка программного обеспечения системы на языке Си

В данной курсовой работе необходимо разработать программу для DSP, реализующую, вынесенные в постановку задачи, звуковые эффекты, но в связи с тем, что цифровой процессор не позволяет обрабатывать вектора длиннее, чем 7000 значений, исходный сигнал был обрезан до 4000, поэтому реализованы были не все звуковые эффекты.

Программа реализации приведена в приложении Б.

6 Результаты реализации звуковых эффектов в среде MatLab и на сигнальном процессоре DSP

Результаты приведены в приложении В, а также представлены в презентации к данной курсовой работе.

7 Краткое руководство пользователя

Для удобства представления результатов работы программ, они были оформлены в презентацию, которая разработана в среде MSPowerPoint. Презентация имеет удобный и интуитивно понятный интерфейс. В неё вынесены методы наложения звуковых эффектов, использованных в курсовой работе, а также результаты – wav-файлы, которые можно прослушать, нажав кнопку . Смена слайдов осуществляется при нажатии кнопок вперед или назад, размещенных в правом нижнем углу.

Заключение

В данной курсовой работе необходимо была разработана в MatLab и CCS система, реализующая звуковые музыкальные эффекты в реальном времени.

В ходе разработки были выявлены основные достоинства и недостатки реализации в различных средах. Так, основной недостаток обработки сигналов на цифровом сигнальном процессоре заключается в том, что процессор не позволяет обрабатывать вектора, длиннее, чем 7000 отсчетов, что и было указано выше. Вследствие этого, не все эффекты удалось реализовать, а реализованные проигрывали в качестве звука эффектам, синтезированным на языке Matlab. Эти недостатки можно устранить, если изменить частоту дискретизации музыкального файла.

Библиографический список

1. Секунов Н.Ю. Обработка звука на РС/ Н.Ю. Секунов. – СПб.: БХВ-Петербург, 2001. – 1248 с.

2. Бондарев В.Н. Цифровая обработка сигналов: методы и средства/ В.Н. Бондарев, Г. Трестер, В.С. Чернега.- Севастопололь: Изд-во СевГТУ, 1999. – 388с.

3. Методические указания к курсовому проектированию по дисциплине "Цифровая обработка сигналов"/ Сост. В.Н. Бондарев, А.Л. Овчинников, B.С. Чернега.– Севастополь: Изд-во СевНТУ, 2003. – 94с.

ПРИЛОЖЕНИЕ А

Текст программ на MatLab

1. Текст программы, реализующей эффект однократной цифровой задержки

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

D=Fs*0.2; %задержка исходного сигнала

z=zeros(1, D);

xz=[z x']; %задержанный сигнал

xx=[x' z];

y=xx+0.5*xz;

wavwrite(y, Fs, bits, 'c:\odnkr_zad.wav');

%Графическое изображение исходного и задержанного сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

axis([1 14000 -1 1]);

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Zadergannuy signal');

%Записываем в отдельный файл отсчеты сигнала

fid=fopen('c:\x.dat','w');

fprintf(fid,'1651 2 0 1 %3d\n',N);

fprintf(fid,'%4d\n',x);

fclose(fid);

2. Текст программы, реализующей эффект многократной цифровой задержки с помощью трансверсального фильтра:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

%Параметры трансверсального фильтра

D1=round(Fs*0.043); a1=0.841;

D2=round(Fs*0.172); a2=0.504;

D3=round(Fs*0.01); a3=0.49;

D4=round(Fs*0.043); a4=0.379;

%Разница между длинами входного и выходного сигналов

D=round(Fs*0.268);

z1=zeros(1,D1);

z2=zeros(1,D2);

z3=zeros(1,D3);

z4=zeros(1,D4);

z=zeros(1,D);

%Сигнал в разных точках трансверсального фильтра

zx=[x', z 0];

xx=[z1 x'];

xz1=[xx z2 z3 z4]; y1=xz1*a1;

xxx=[z2 xx];

xz2=[xxx z3 z4]; y2=xz2*a2;

xxxx=[z3 xxx];

xz3=[xxxx z4]; y3=xz3*a3;

xxxxx=[z4 xxxx];

xz4=[xxxxx]; y4=xz4*a4;

y=zx+y1+y2+y3+y4;

wavwrite(y, Fs, bits, 'c:\mnog_trans.wav');

%Графическое изображение исходного и задержанного сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

axis([1 16000 -1 1]);

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Zadergannuy signal');

3. Текст программы, реализующей эффект многократной цифровой задержки с помощью рекурсивного фильтра:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

%Параметры рекурсивного фильтра

D=round(Fs*0.15); a=0.8;

z=zeros(1,D);

xx=[x' z z z z z z z z z];

x1=x*a;

x2=x1*a;

x3=x2*a;

x4=x3*a;

x5=x4*a;

x6=x5*a;

x7=x6*a;

x8=x7*a;

x9=x8*a;

y1=[zx1' zzzzzzzz]; %задержки исходного сигнала

y2=[zzx2' zzzzzzz];

y3=[zzzx3' zzzzzz];

y4=[zzzzx4' zzzzz];

y5=[zzzzzx5' zzzz];

y6=[zzzzzzx6' zzz];

y7=[zzzzzzzx7' zz];

y8=[zzzzzzzzx8' z];

y9=[zzzzzzzzzx9'];

y=xx+y1+y2+y3+y4+y5+y6+y7+y8+y9;

wavwrite(y, Fs, bits, 'c:\mnog_rec.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

axis([1 40000 -2 2]);

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

4. Текст программы, реализующей эффект детонации:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

%Diapazon izmenenia zadergki

D=round(Fs*0.025);

z=zeros(1,D);

xx=[x' z];

for i=1:N

fn=round(D*0.5*(1+cos(2*pi*i/3)));

y(1,i)=0.5*xx(1,i)+xx(1,fn+i); %разностное уравнение

end

wavwrite(y, Fs, bits, 'c:\detonacia.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

5. Текст программы, реализующей эффект хора:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

D=round(Fs*0.035);

z=zeros(1,D);

for i=1:4000

u(1,i)=x(i,1);

end;

x= [u z];

for n=1:4000

fn1=round(D*0.5*(1+cos(2*pi*n/50))); %Zadergki kagdogo instrumenta

fn2=round(D*0.5*(1+cos(2*pi*n/10)));

fn3=round(D*0.5*(1+cos(2*pi*n/100)));

fn4=round(D*0.5*(1+cos(2*pi*n/1000)));

y(1,n)=0.2*x(1,n)+0.2*x(1,fn1+n)+0.2*x(1,fn2+n)+0.2*x(1,fn3+n)+0.2*x(1,fn4+n);

end

wavwrite(y, Fs, bits, 'c:\xor.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(xx),grid on;title('Isxodnuy signal');

axis([0 4000 -1 1]);

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

6. Текст программы, реализующей эффект вибрато:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

D=round(Fs*0.035);

z=zeros(1,D);

x= [x' z];

for n=1:N

fn=round(D*0.5*(1+cos(2*pi*n/5))); %Zadergka

y(1,n)=0.8*x(1,fn+n);

end

wavwrite(y, Fs, bits, 'c:\vibratto.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

axis([0 10000 -1 1]);

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

7. Текст программы, реализующей эффект компрессора:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

a=0.3;

for n=1:N

if(abs(x(n,1))<=a)

y(1,n)=x(n,1);

end;

if(abs(x(n,1))>a)

y(1,n)=x(n,1)/abs(x(n,1))*abs(x(n,1))*a;

end

wavwrite(y, Fs, bits, 'c:\kompress.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

axis([0 10000 -1 1]);

8. Текст программы, реализующий эффект экспандера:

clc;

%считываем исходный файл

[x,Fs,bits]=wavread('c:\1.wav');

N=size(x);

a=0.3;

for n=1:N

if(abs(x(n,1))>a)

y(1,n)=x(n,1);

end;

if(abs(x(n,1))<=a)

y(1,n)=x(n,1)/abs(x(n,1))*abs(x(n,1))/a;

end

wavwrite(y, Fs, bits, 'c:\exspand.wav');

%Графическое изображение исходного и результирующего сигналов во временной области

figure(1);

subplot(2,1,1);

plot(x),grid on;title('Isxodnuy signal');

figure(1);

subplot(2,1,2);

plot(y),grid on;title('Resyltiryushiy signal');

axis([0 10000 -1 1]);

ПРИЛОЖЕНИЕ Б

Текст программ на Си

1. Текст программы, реализующей эффект однократной цифровой задержки:

float input_x[4000];

float output_y[6200];

void dataIN(void){}

void dataOUT(void){}

main()

{

int i;

float xx[6200];

float y1[6200];

while(1)

{

dataIN();

for (i=0; i<2200; i++)

y1[i]=0;

for (i=2200; i<6200; i++)

y1[i]=input_x[i];

for (i=0; i<4000; i++)

xx[i]=input_x[i];

for (i=4000; i<6200; i++)

xx[i]=0;

for(i=0; i<=6200; i++)

output_y[i]=xx[i]+0.5*y1[i];

dataOUT();

}

return 0;

}

2. Текст программы, реализующей эффект детонации:

float input_x[4000];

float output_y[4000];

void dataIN(void){}

void dataOUT(void){}

main()

{

int i;

float xx[6200];

float y1[6200];

int D=550;

int fn;

while(1)

{

dataIN();

for (i=0; i<4000; i++)

xx[i]=input_x[i];

for (i=4000; i<4550; i++)

xx[i]=0;

for (i=0; i<4000; i++)

{

fn=(D*0.5*(1+cos(2*3.14*i/3)));

output_y[i]=0.5*xx[i]+xx[i+fn];

}

dataOUT();

}

return 0;

}

3. Текст программы, реализующей эффект хора:

float input_x[4000];

float output_y[4000];

void dataIN(void){}

void dataOUT(void){}

main()

{

int i;

float xx[4770];

int D=770;

int fn1; int fn2; int fn3; int fn4;

while(1)

{

dataIN();

for (i=0; i<4000; i++)

xx[i]=input_x[i];

for (i=4000; i<4770; i++)

xx[i]=0;

for (i=0; i<4000; i++)

{

fn1=(D*0.5*(1+cos(2*3.14*i/50)));

fn2=(D*0.5*(1+cos(2*3.14*i/10)));

fn3=(D*0.5*(1+cos(2*3.14*i/100)));

fn4=(D*0.5*(1+cos(2*3.14*i/1000)));

output_y[i]=0.2*xx[i]+0.2*xx[i+fn1]+0.2*xx[i+fn2]+0.2*xx[i+fn3]+0.2*xx[i+fn4];

}

dataOUT();

}

return 0;

}

4. Текст программы, реализующей эффект компрессора:

float input_x[4000];

float output_y[4000];

void dataIN(void){}

void dataOUT(void){}

main()

{

int i;

float a;

a=0.3; //koefficient kompressii

while(1)

{

dataIN();

for (i=0; i<4000; i++)

{

if(abs(x[i])<=a)

y[i]=x[i];

if(abs(x[i])>a)

ourput_y[i]=(x[i]/abs(x[i]))*abs(x[i])*a

}

dataOUT();

}

return 0;

}

ПРИЛОЖЕНИЕ В

Результаты курсового проектирования

Результатами выполнении задания на курсовое проектирование являются звуковые файлы, соответствующие изменению исходного сигнала при различных эффектах. Эти файлы представлены в презентации курсового проекта. В пояснительную записку вошли графики исходного и результирующих сигналов при обработке в MatLab и на ЦСП.

1. Графики исходного и результирующего сигнала при реализации эффекта однократной задержки на MatLab и на ЦСП представлены на рисунке В.1 и В.2:

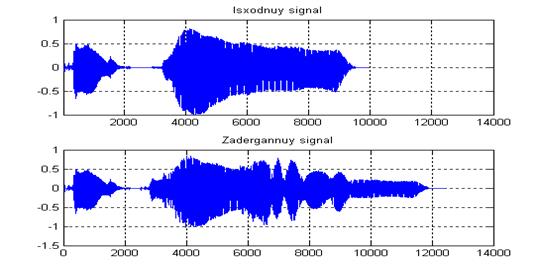
Рисунок В.1—Исходный и результирующий сигнал при однократной задержке на MatLab

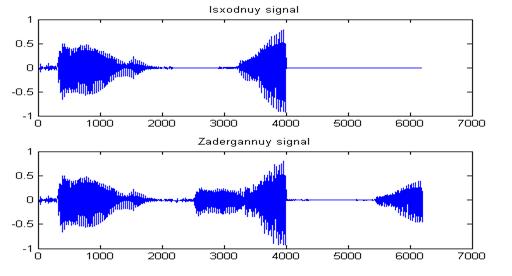
Рисунок В.2—Исходный и результирующий сигнал при однократной задержки на ЦСП

2. Графики исходного и результирующего сигнала при реализации эффекта многократной задержки с помощью трансверсального и рекурсивного фильтров на MatLabпредставлены на рисунке В.3 и В.4:

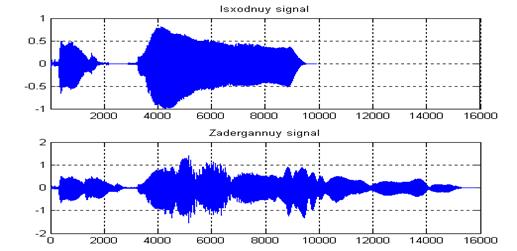
Рисунок В.3—Исходный и результирующий сигнал при многократной задержке с помощью трансверсального фильтра на MatLab

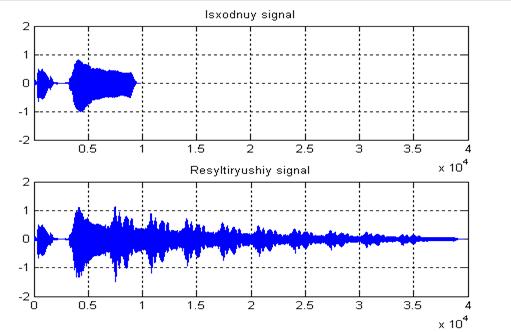
Рисунок В.4—Исходный и результирующий сигнал при многократной задержке с помощью рекурсивного фильтра на MatLab

3. Графики исходного и результирующего сигнала при реализации эффекта детонации на MatLab и на ЦСП представлены на рисунке В.5 и В.6:

Рисунок В.5—Исходный и результирующий сигнал при детонации на MatLab

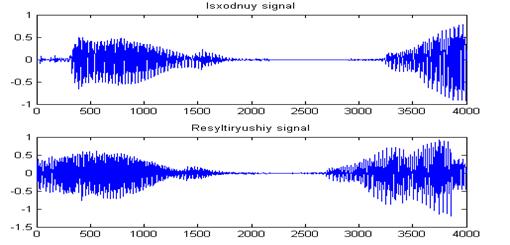
Рисунок В.5—Исходный и результирующий сигнал при детонации на ЦСП

4. Графики исходного и результирующего сигнала при реализации эффекта хора на MatLab и на ЦСП представлены на рисунке В.7 и В.8:

Рисунок В.7—Исходный и результирующий сигнал при реализации эффекта хора на MatLab

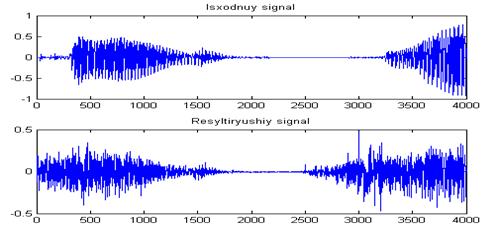
Рисунок В.8—Исходный и результирующий сигнал при реализации эффекта хора на ЦСП

5. Графики исходного и результирующего сигнала при реализации эффекта вибрато на MatLab представлены на рисунке В.9:

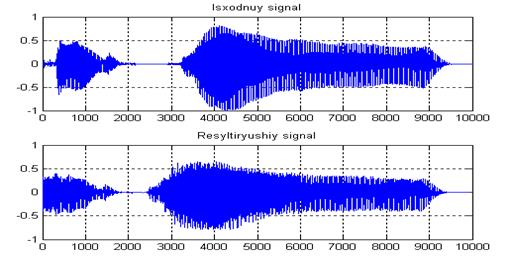
Рисунок В.9—Исходный и результирующий сигнал при реализации эффекта вибрато на MatLab

6. Графики исходного и результирующего сигнала при реализации компрессора на MatLab и на ЦСП представлены на рисунке В.10 и В.11:

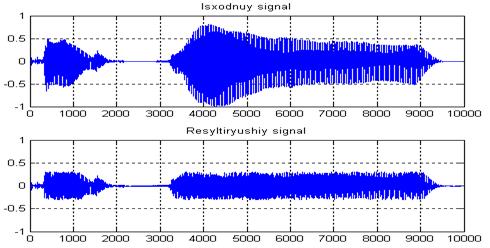
Рисунок В.10—Исходный и результирующий сигнал при реализации компрессора на MatLab

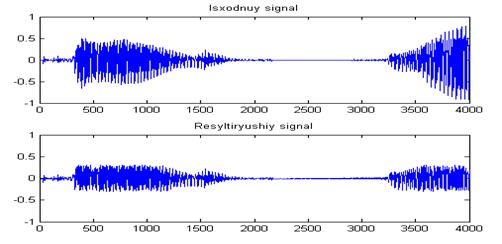
Рисунок В.11—Исходный и результирующий сигнал при реализации коспрессора на ЦСП

7. Графики исходного и результирующего сигнала при реализации экспандера на MatLab В.12:

Рисунок В.12—Исходный и результирующий сигнал при реализации экспандера на MatLab