| Скачать .docx |
Реферат: Использование современной компьютерной техники и программного обеспечения при исследовании химик
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
КУРСОВАЯ РАБОТА
По дисциплине:______________________Информатика ______________________________
(наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема: Использование современной компьютерной техники и программного обеспечения при исследовании химико-технологического процесса
Автор: студент гр. АПМ-07-2 _______________ / Лебедик Н .В. /
(подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: ___________________
ПРОВЕРИЛ:
Руководитель проекта: доцент ________________ / Головенчиц Н.Я. /
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2008 год
| Федеральное агентство по образованию |
||
| Государственное образовательное учреждение Высшего профессионального образования Санкт-Петербургский государственный горный институт им Г.В. Плеханова (технический университет) |
||
| УТВЕРЖДАЮ Заведующий кафедрой /_____/ доц. Прудинский А. Г. / "___"__________2008г. |
||
Кафедра Информатики и компьютерных технологий.
КУРСОВАЯ РАБОТА
По дисциплине: Информатика ____________________
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
студенту группы АПМ-07-2 Лебедик Н .В.
(шифр группы) (Ф.И.О.)
1. Тема работы: Использование современной компьютерной техники и программного обеспечения при исследовании химико-технологического процесса
2. Исходные данные к работе: Изложены в методических указаниях
3. Содержание пояснительной записки: Требования к содержанию пояснительной записки изложены в методических указаниях.
4. Срок сдачи законченной работы: ___ декабря 2008 г.
Руководитель проекта: доцент ________________ /Головенчиц Н.Я. /
(должность) (подпись) (Ф.И.О.)
Дата выдачи задания: 24 сентября 2008 г.
1. Первичная обработка наблюдений двух измеримых признаков исследуемого объекта. - 4 -
1.1 Содержательная формулировка задачи. - 4 -
1.2 Исходные данные (таблица 1) - 4 -
1.4 Разработка алгоритма решения задачи. - 9 -
2. Контрольный вариант. - 11 -
2.1 Нахождение уравнений регрессии. - 15 -
2.2 Нахождение уравнения регрессии с помощью метода наименьших квадратов. - 16 -
2.3 Нахождение коэффициентов детерминированности. - 17 -
2.4 Построение графиков зависимостей и линии тренда. - 18 -
3. Вычисление с помощью среды Turbo Pascal - 20 -
3.2. Контрольный вариант. - 22 -
3.6. Результаты выполнения программы и их анализ. - 24 -
Библиографический список. - 26 -
1. Первичная обработка наблюдений двух измеримых признаков исследуемого объекта.
1.1 Содержательная формулировка задачи .
При исследовании некоторого технологического процесса часто возникает задача оценки одновременного изменения содержания двух химических элементов или соединений, характеризующих этот процесс. В результате исследований получают ряд наблюдений, каждое из которых содержит значение двух изучаемых величин, обычно обозначаемых ![]() и
и ![]() , и называемых измеримыми признаками.
, и называемых измеримыми признаками.
При этом может иметь место один из трёх случаев:
1) С увеличением содержания одного химического элемента (соединения) содержание другого химического элемента (соединения) также возрастает;
2) С увеличением содержания одного химического элемента (соединения) содержание другого уменьшается;
3) С увеличением содержания одного химического элемента (соединения) содержание другого не изменяется.
Для наглядного представления полученных экспериментальных данных строят точечную диаграмму, где положение каждой точки определяется двумя координатами – соответствующими значениями ![]() и
и ![]() .
.
Часто взаимное изменение значений ![]() и
и ![]() может быть описано линейной функцией. Нахождение уравнения прямой линии, называемой линией регрессии, относительно которой располагаются значения
может быть описано линейной функцией. Нахождение уравнения прямой линии, называемой линией регрессии, относительно которой располагаются значения ![]() и
и ![]() , является целью исследования.
, является целью исследования.
Для нахождения уравнения линии регрессии при достаточно большом числе наблюдений строят вспомогательную (корреляционную) таблицу и находят ряд математических характеристик признаков ![]() и
и ![]() .
.
1.2 Исходные данные (таблица 1)
При определении оптимальных условий технологического процесса получения волокна из пропилена изучалось влияние температуры расплава ![]() на прочность волокна
на прочность волокна ![]() .
.
Результаты испытаний представлены в таблице 1
Таблица 1
Температура расплава и прочность волокна
|
|
145 |
146 |
146 |
153 |
149 |
150 |
151 |
147 |
154 |
150 |
|
|
52,2 |
52,3 |
56,4 |
62,1 |
59,1 |
58,5 |
61,1 |
52,3 |
64,1 |
57,9 |
|
|
151 |
148 |
148 |
147 |
150 |
148 |
154 |
155 |
153 |
151 |
|
|
59,1 |
59,4 |
53,8 |
54,1 |
55,5 |
56,8 |
63,1 |
64,3 |
65,3 |
59,3 |
|
|
148 |
149 |
148 |
150 |
150 |
151 |
153 |
152 |
154 |
152 |
|
|
56,2 |
55,2 |
54,7 |
58,5 |
58,1 |
61,8 |
60,9 |
60,3 |
63,1 |
62,0 |
Найти корреляционную зависимость прочности волокна от температуры расплава.
1) Построение корреляционной таблицы.
Для построения корреляционной таблицы результаты наблюдений по каждому признаку ![]() и
и ![]() разбивают на интервалы, число которых можно определить по формуле
разбивают на интервалы, число которых можно определить по формуле
![]() , (1.3.1)
, (1.3.1)
где ![]() - число интервалов,
- число интервалов, ![]() - число наблюдений соответствующего признака. Далее находят длины интервалов
- число наблюдений соответствующего признака. Далее находят длины интервалов ![]() и
и ![]() :
:
![]() ,
, ![]() ;
;
Число интервалов по признакам ![]() и
и ![]() может быть одинаково.
может быть одинаково.
Общий вид корреляционной таблицы представлен в таблице 2.а). В этой таблице указывают длины отдельных интервалов по признакам ![]() и
и ![]() , середины интервалов, в клетках таблицы помещают число наблюдений, попавших в определённые интервалы сразу по двум признакам
, середины интервалов, в клетках таблицы помещают число наблюдений, попавших в определённые интервалы сразу по двум признакам ![]() и
и ![]() , далее находят число наблюдений, попавших в определённый интервал по признаку
, далее находят число наблюдений, попавших в определённый интервал по признаку ![]() и
и ![]() соответственно, а также условные средние значения.
соответственно, а также условные средние значения.
В таблице 2.а) введены следующие обозначения:
![]() - середины интервалов по признакам
- середины интервалов по признакам ![]() и
и ![]() соответственно,
соответственно, ![]() где
где ![]() - число классов);
- число классов);
![]() - число наблюдений, попавших в интервал
- число наблюдений, попавших в интервал ![]() по признаку
по признаку ![]() и в интервал
и в интервал ![]() по признаку
по признаку ![]() ;
;
![]() - число наблюдений, попавших в интервал
- число наблюдений, попавших в интервал ![]() по признаку
по признаку ![]() ;
;
Таблица 2.а)
Корреляционная таблица
|
|
|
|
|
|
|
|
|||
|
|
|
… |
|
… |
|
||||
|
|
|
|
|
… |
|
… |
|
|
|
|
|
|
|
|
… |
|
… |
|
|
|
| ….. |
….. |
….. |
… |
….. |
… |
….. |
… |
….. |
|
|
|
|
|
|
… |
|
… |
|
|
|
| ….. |
… |
….. |
….. |
… |
….. |
… |
….. |
… |
….. |
|
|
|
|
|
… |
|
… |
|
|
|
|
|
|
|
… |
|
… |
|
|
||
|
|
|
|
… |
|
… |
|
![]() - число наблюдений, попавших в интервал
- число наблюдений, попавших в интервал ![]() по признаку
по признаку ![]() ;
;
![]() - условные средние значения признака
- условные средние значения признака ![]() для наблюдений, попавших в интервал
для наблюдений, попавших в интервал ![]() по признаку
по признаку ![]() ;
;
![]() - условные средние значения признака
- условные средние значения признака ![]() для наблюдений, попавших в интервал
для наблюдений, попавших в интервал ![]() по признаку
по признаку ![]() ;
;
![]() - число наблюдений.
- число наблюдений.
Отметим, что при вычислениях условных средних значений, а также других математических характеристик признаков ![]() и
и ![]() , всем наблюдениям, попавшим в некоторый интервал, придаётся значение середины этого интервала.
, всем наблюдениям, попавшим в некоторый интервал, придаётся значение середины этого интервала.
Значения ![]() находят, суммируя число наблюдений, попавших в соответствующие интервалы по признаку
находят, суммируя число наблюдений, попавших в соответствующие интервалы по признаку ![]() соответственно. Вычисления производят по формулам:
соответственно. Вычисления производят по формулам:
![]()
![]()
где ![]() -число интервалов.
-число интервалов.
В нижней строке и в последнем столбце таблицы представлены условные средние значения, вычисленные по формулам:
![]()
![]()
Рассмотрим линейную связь ![]() и
и ![]() .
.
2) Вычисление коэффициента корреляции, нахождение уравнения регрессии.
Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо, в среднем, может быть представлена одна из величин в виде линейной функции от другой.
Коэффициент корреляции по абсолютной величине не превосходит 1. Чем ближе ![]() к единице, тем линейная связь между величинами
к единице, тем линейная связь между величинами ![]() и
и ![]() считается более тесной. Отметим, что вычисления по формулам (2) и (3) производятся по данным, не объединённым в группы. Если число наблюдений велико, коэффициент корреляции и другие математические характеристики системы величин
считается более тесной. Отметим, что вычисления по формулам (2) и (3) производятся по данным, не объединённым в группы. Если число наблюдений велико, коэффициент корреляции и другие математические характеристики системы величин ![]() находят по группированным данным.
находят по группированным данным.
Так, расчёт коэффициента корреляции по группированным данным, выполняется по формуле
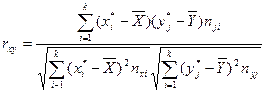 , (1.3.2)
, (1.3.2)
где ![]() (1.3.3)
(1.3.3)
Все величины в этих формулах должны быть взяты из корреляционной таблицы.
Уравнение прямой линии, относительно которой наилучшим образом расположены условные средние значения ![]() , а также отдельные точки с координатами
, а также отдельные точки с координатами ![]() , может быть найдено по формуле
, может быть найдено по формуле
![]() (1.3.4)
(1.3.4)
Величины, входящие в уравнение (4), могут быть найдены по данным, объединённым в группы.
При вычислениях по группированным данным величины ![]() и
и ![]() вычисляются по таким формулам:
вычисляются по таким формулам:
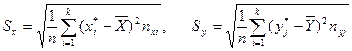 (1.3.5)
(1.3.5)
Уравнение линейной регрессии может быть найдено методом наименьших квадратов. В случае двух переменных ![]() уравнение линейной регрессии представлено многочленом первой степени.
уравнение линейной регрессии представлено многочленом первой степени.
![]() .
.
Неизвестные параметры ![]() определяются методом наименьших квадратов, исходя из требования
определяются методом наименьших квадратов, исходя из требования
![]() .
.
Найдя частные производные данного выражения по ![]() , и приравняв их к нулю, получим систему нормальных уравнений для определения неизвестных параметров
, и приравняв их к нулю, получим систему нормальных уравнений для определения неизвестных параметров ![]() и
и ![]() .
.
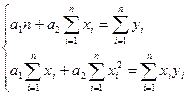 (1.3.6)
(1.3.6)
Данная система линейных алгебраических уравнений может быть решена матричным методом или методом Крамера.
3) Вычисление коэффициента детерминированности
Для количественной оценки соответствия теоретической линии регрессии эмпирическим данным используется коэффициент детерминированности ![]() , вычисляемый по формуле
, вычисляемый по формуле
![]() ,
,
где ![]() и
и ![]() - суммы квадратов, вычисляемые соответственно по формулам:
- суммы квадратов, вычисляемые соответственно по формулам:
![]() (1.3.7)
(1.3.7)
где ![]() - данные эмпирические значения признака
- данные эмпирические значения признака ![]() ,
,
![]() - среднее арифметическое значение
- среднее арифметическое значение ![]() ,
,
![]() - теоретическое значение признака
- теоретическое значение признака ![]() , вычисленное при подстановке соответствующего значения
, вычисленное при подстановке соответствующего значения ![]() в найденное уравнение регрессии.
в найденное уравнение регрессии.
Обычно коэффициент детерминированности лежит между 0 и 1. Чем ближе этот коэффициент к 1, тем лучше найденная линия регрессии представляет экспериментальные данные, положенные в основу расчётов.
1.4 Разработка алгоритма решения задачи
Чтобы решить поставленную задачу, необходимо воспользоваться следующим алгоритмом:
1) По результатам наблюдений двух измеримых признаков (X,Y) построить вспомогательную ( корреляционную ) таблицу, распределив значения X,Y на 5-6 интервалов. Найти условные средние значения ![]() ,
,![]() . Корреляционную таблицу можно построить вручную.
. Корреляционную таблицу можно построить вручную.
2) Вычислить значение коэффициента корреляции по группированным данным, используя формулы.
3) Найти уравнение регрессии, используя формулы.
4) Найти уравнение регрессии методом наименьших квадратов.
5) По данным значениям переменных построить точечную диаграмму, указать на ней линию тренда. При построении линии тренда с помощью вкладки «Параметры» показать на диаграмме уравнение линии тренда и величину R2 .
6) Найти теоретические значения Y, подставив данные значения xi в уравнение регрессии, найденное в пункте 3.
7) Построить графики условных средних значений ![]() (
(![]() ) , а также график теоретических значений Y на одной диаграмме.
) , а также график теоретических значений Y на одной диаграмме.
8) Найти коэффициент детерминированности для уравнения регрессии, найденного в пункте 3.
9) Найти коэффициент детерминированности для уравнения регрессии, найденного в пункте 3.
2. Контрольный вариант
Для того чтобы найти уравнение регрессии средствами MS Excel создадим сначала необходимые таблицы. В первую очередь необходимо рассчитать необходимые параметры для составления корреляционной таблицы.
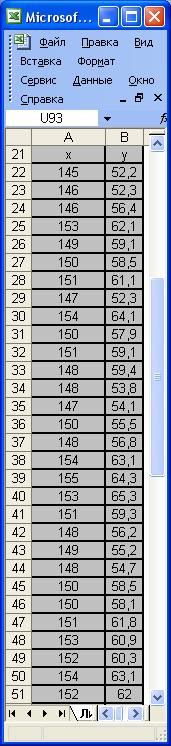
Рис.1 Фрагмент окна Excel c табличными данными х и у.
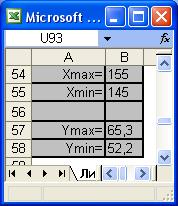
Рис.2 Фрагмент окна Excel, отображающий максимальное и минимальное значения х и у.
Пояснения:
1) В ячейки A22:A51 в ячейки B22:B51 вводим значения X и Y.
2) Для расчёта средних значений первоначальных данных X и Y в ячейку A52 вводим формулу =СУММ(A22:A51)/30, а в ячейку B52 вводим формулу =СУММ(B22:B51)/30.
3) Чтобы рассчитать максимальное и минимальное значение X, в ячейки B54 и B55 вводим формулы =МАКС(A22:A51) и =МИН(A22:A51) соответственно.
4) Аналогично, чтобы рассчитать максимальное и минимальное значение Y, в ячейки B57 и B58 вводим формулы =МАКС(B22:B51) и =МИН(B22:B51) соответственно.
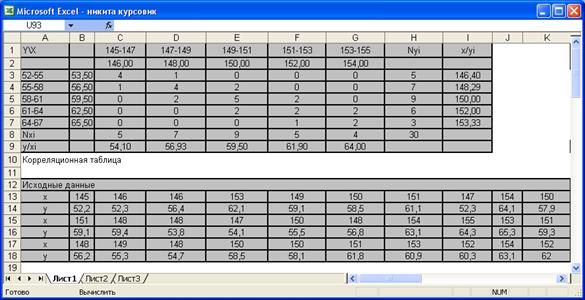
Рис.3 Фрагмент окна Excel, отображающий исходные данные и корреляционную таблицу.
Пояснения:
Используя начальные данные можно составить корреляционную таблицу.
1) В ячейки C1:G1 и в ячейки A3:A7 вводим интервалы изменения исходных значений X и Y.
2) В ячейки C2:G2 вводим середины интервалов по признаку X
3 В ячейки B3:B7 вводим середины интервалов по признаку Y.
4) В ячейку H3 вводим формулу =СУММ(C3:G3) и копируем её в ячейки H4:H7.
5) В ячейку C8 вводим формулу =СУММ(C3:C7) и копируем её в ячейки D8:H8.
6) В ячейку C9 вводим формулу =(B3*C3+B4*C4+B5*C5+B6*C6+B7*C7)/C8.
7) В ячейку D9 вводим формулу =(B3*D3+B4*D4+B5*D5+B6*D6+B7*D7)/D8.
8) В ячейку E9 вводим формулу =(B3*E3+B4*E4+B5*E5+B6*E6+B7*E7)/E8.
9) В ячейку F9 вводим формулу =(B3*F3+B4*F4+B5*F5+B6*F6+B7*F7)/F8.
10) В ячейку I3 вводим формулу =(C2*C3+D2*D3+E2*E3+F2*F3+G2*G3)/H3.
11) В ячейку I4 вводим формулу =(C2*C4+D2*D4+E2*E4+F2*F4+G2*G4)/H4.
12) В ячейку I5 вводим формулу =(C2*C5+D2*D5+E2*E5+F2*F5+G2*G5)/H5.
13) В ячейку I6 вводим формулу =(C2*C6+D2*D6+E2*E6+F2*F6+G2*G6)/H6.
14) В ячейку I7 вводим формулу =(C2*C7+D2*D7+E2*E7+F2*F7+G2*G7)/H7.
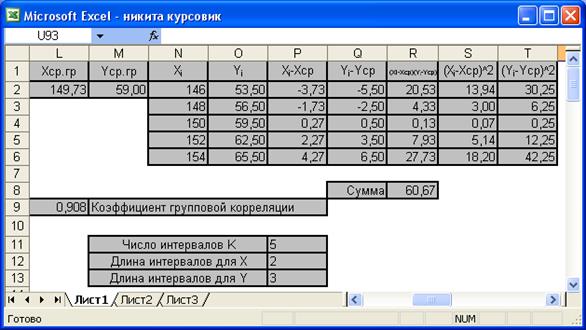
Рис.4 Фрагмент окна Excel, отображающий вычисление среднего значения х и у и коэффициента групповой корреляции.
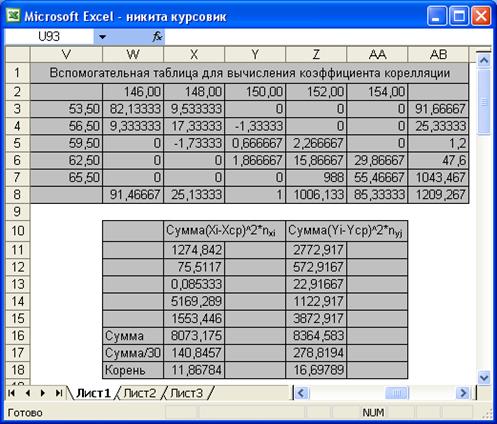
Рис.5 Фрагмент окна Excel, отображающий вспомогательную таблицу для вычисления коэффициента корреляции.
Пояснения:
1) В ячейку L2 вводим формулу
=(C2*C8+D2*D8+E2*E8+F2*F8+G2*G8+H2*H8)/30.
2) В ячейку M2 вводим формулу
=(B3*H3+B4*H4+B5*H5+B6*H6+B7*H7+B8*H8)/30.
3) В ячейки N2:N6 и в ячейки O2:O6 вводим соответствующие средние интервальные значения X и Y.
4) В ячейку P2 вводим формулу =N2-$L$2 и копируем её в ячейки P3:P6.
5) В ячейку Q2 вводим формулу =O2-$M$2 и копируем её в ячейки Q3:Q6.
6) В ячейку R2 вводим формулу =P2*Q2, затем в ячейку R3 вводим формулу =P3*Q3 и т.д. до ячейки R6.
7) В ячейку R8 вводим формулу =СУММ(R2:R6).
8) В ячейку S2 вводим формулу =P2^2 и копируем её в ячейки S3:S6.
9) В ячейку T2 вводим формулу =Q2^2 и копируем её в ячейки T3:T6.
10) В ячейку W3 вводим формулу =(W2-$L$2)*($V$3-$M$2)*C3 и копируем её до ячейки АА3.
11) В ячейку W4 вводим формулу =(W2-$L$2)*($V$4-$M$2)*C4 и копируем её до ячейки АА4.
12) В ячейку W5 вводим формулу =(W2-$L$2)*($V$5-$M$2)*C5 и копируем её до ячейки АА5.
13) В ячейку W6 вводим формулу = (W2-$L$2)*($V$6-$M$2)*C6 и копируем её до ячейки АА6.
14) В ячейку W7 вводим формулу = (W2-$L$3)*($V$7-$M$2)*C7 и копируем её до ячейки АА7.
15) В ячейку X11 вводим формулу = S2*$W$8, копируем её до ячейки X15.
16) В ячейку Z11 вводим формулу = T2*$AB$3, копируем её до ячейки Z15
17) В ячейку V16 вводим формулу = СУММ(V11:V15).
18) В ячейку X16 вводим формулу =СУММ(X11:X15).
19) В ячейку Z16 вводим формулу = СУММ(Z11:Z15).
20) В ячейку X17 вводим формулу =X16/30.
21) В ячейку Z17 вводим формулу =Z16/30.
22) В ячейку X18 вводим формулу =КОРЕНЬ(X17).
23) В ячейку Z18 вводим формулу =КОРЕНЬ(Z17)
24) В ячейку L9 введём формулу =AB8/(X18*Z18). В этой ячейке будет находиться значение коэффициента корреляции для группированных данных.
2. 1 Нахождение уравнений регрессии.
1) Найдём уравнение регрессии по группированным данным.
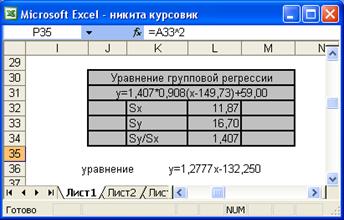
Для того чтобы вычислить коэффициенты уравнения регрессии по группированным данным необходимо вычислить значение параметров по формулам, приведенным в теории.
| |
Пояснения:
1) В ячейку L32 вводим формулу =Х18.
2) В ячейку L33 вводим формулу =Z18.
3) В ячейку L34 вводим формулу =L33/L32.
В итоге получили уравнение регрессии по групповым данным:
У=1,2777Х-132,250
2.2 Нахождение уравнения регрессии с помощью метода наименьших квадратов.
Аппроксимируем функцию ![]() линейной функцией
линейной функцией ![]() . Найдем коэффициенты a1
и a2
.
. Найдем коэффициенты a1
и a2
.
1) В ячейку P24 вводим формулу =A22^2 и копируем её в ячейки P25:P53.
2) В ячейку Q24 вводим формулу =A22*B22 и копируем её в ячейки Q25:Q53.
3) В ячейку R24 вводим формулу =A22 и копируем её в ячейки R25:R53
В ячейку T24 вводим формулу =$L$9*$L$34*(R24-$L$2)+$M$2 и копируем её в ячейки T25:T53.
В ячейку W24 вводим формулу =(B22-V24)^2 и копируем её в ячейки W25:W53.
В ячейку Z24 вводим формулу =(B22-T24)^2 и копируем её в ячейки Z25:Z53.
4) В ячейку P54 вводим формулу =СУММ(P24:P53)
5) В ячейку Q54 вводим формулу =СУММ(Q24:Q53).
| |
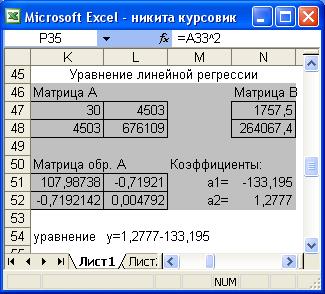
Рис.7 Фрагмент окна Excel, отображающий полученное уравнение линейной регрессии.
В итоге получили уравнение регрессии по групповым данным: y=1,2777X-133,195.
2.3 Нахождение коэффициентов детерминированности.
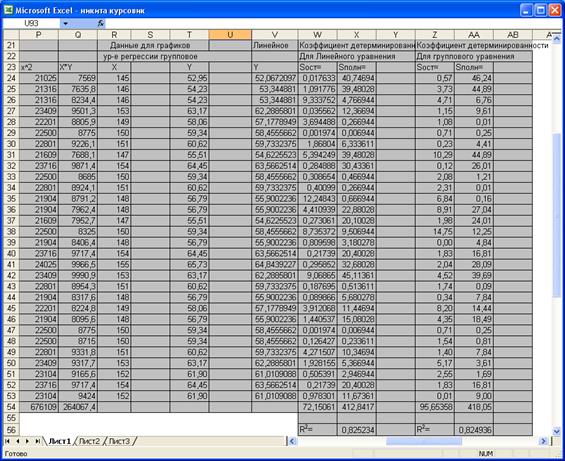
Рис.8 Фрагмент окна Excel, отображающий вычисление коэффициента детерминированности для линейного и группового уравнений.
Пояснения:
Для линейного уравнения
1) В ячейку W24 вводим формулу =(B22-V24)^2 и копируем её в ячейки W25:W53.
Для группового уравнения
2) В ячейку Z24вводим формулу =(B22-T24)^2 и копируем её в ячейки Z25:Z53.
3) В ячейку Х24 вводим формулу =(B22-$B$52)^2 и копируем её в ячейки Х25:Х53.
4) В ячейку АА24 вводим формулу =(B22-$M$2)^2 и копируем её в ячейки АА25:АА53.
5) В ячейку W54 вводим формулу =СУММ(W24:W53).
6) В ячейку X54 вводим формулу =СУММ(X24:X53).
7) В ячейку Z54 вводим формулу =СУММ(Z24:Z53).
8) В ячейку AA54 вводим формулу =СУММ(AA24:AA53).
9) В ячейку W56 вводим формулу =1-W54/X54 .
10) В ячейку Z56 вводим формулу =1-Z54/AA54.
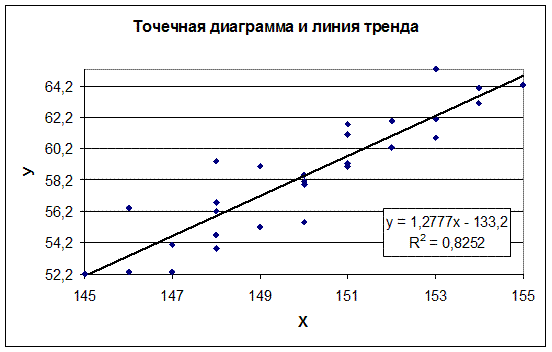
2.4 Построение графиков зависимостей и линии тренда
|
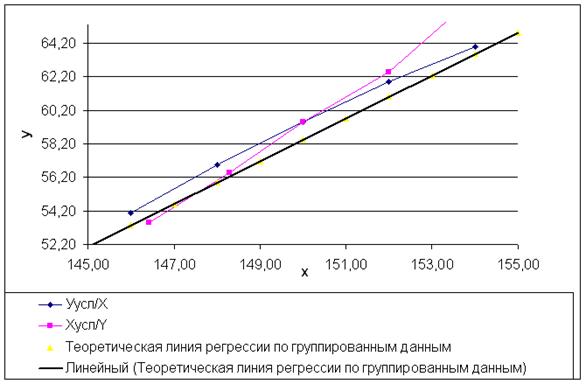
Рис.10: График зависимостей
3. Вычисление с помощью среды Turbo Pascal
В данной задаче требуется с помощью подпрограммы вычислить Sx, Sy по данным, объединенным в группы, по формулам: 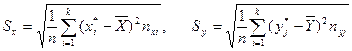 . Составим подпрограмму процедуру величины.
. Составим подпрограмму процедуру величины. 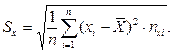
Пусть n – количество измеренных параметров,
i = 1, 2, …, n, где i – текущий индекс,
p = (p1, p2, …, pn ) – массив чисел,
zср – средние значения элементов массива p;
Обозначим: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
Результат: ![]() , где
, где ![]() - выходной параметр.
- выходной параметр.
Описание формальных параметров и переменных для подпрограммы представлены в таблице 3.2.
Таблица 3.2
Таблица формальных параметров и переменных подпрограммы
| Имя переменной |
Тип переменной |
Примечание |
| p |
Mas |
массив чисел |
| zср |
Real |
средние значения элементов массива p |
| s |
Real |
|
| scp |
Real |
|
| sq |
Real |
выходные данные |
| i |
Integer |
текущий индекс |
Описание переменных программы представлены в таблице 3.3.
Таблица 3.3
Таблица переменных программы
| Имя переменной |
Тип переменной |
Примечание |
| f |
Text |
файловые переменные |
| x |
Mas |
массив чисел Xi |
| y |
Mas |
массив чисел Yi |
| i |
Integer |
текущий индекс |
| S1 |
Real |
результат вычисления |
| S2 |
Real |
результат вычисления |
Контрольный вариант представлен в табличном процессоре Excel, в разделе 2.
Схема алгоритма программы представлена на рисунке 11.
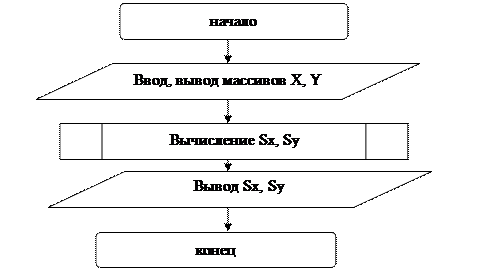
Рис.11. Схема алгоритма программы
Схема алгоритма подпрограммы представлена на рисунке 12:
![]() вход
вход
|
|||||
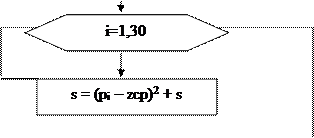 |
|||||
|
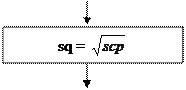 |
выход
Рис.12. Схема алгоритма подпрограммы
Program Nikita; {программа расчета Sx, Sy}
uses crt; {очистка экрана}
type {раздел описания переменных}
mas=array[1..30] of real;
var
i,n:integer;
x,y:mas;
s1,s2:real;
f:text;
{тело процедуры}
Procedure ssxy(n:integer;p:mas;zcp:real; var sq:real); {выходные параметры}
var {раздел описания переменных процедуры}
s,scp:real;
i:integer;
Begin
s:=0.0; {задание начального значения s}
for i:=1 to 30 do {накопление суммы}
s:=sqr(p[i]-zcp)+s;
scp:=s; {вычисление по формуле ![]() }
}
sq:=sqrt(scp); { вычисление по формуле 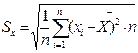 }
}
end;
begin {тело программы}
clrscr; {очистка экрана}
assign(f,'1.txt'); {соединение с файлом}
reset(f); {открытие файла для чтения}
for i:=1 to 30 do read(f,x[i]); {чтение массива Х из файла}
for i:=1 to 30 do read(f,y[i]); {чтение массива Y из файла}
close(f); {закрытие файла}
writeln('mas X'); {вывод массива Х}
writeln('---------------------------------');
for i:=1 to 30 do write(' ',x[i]:6:2);
writeln;
writeln('mas Y'); {вывод массива Y}
writeln('---------------------------------');
for i:=1 to 30 do write(' ',y[i]:6:2);
writeln;
ssxy(30,x,150.1,s1); {использование процедуры для расчета S1}
ssxy(30,y,58.6,s2); {использование процедуры для расчета S1}
writeln('S1= ',s1:6:2); {вывод S1}
writeln('S2= ',s2:6:2); {вывод S2}
readln;
end.
Для отладки программы воспользуемся исходными значениями, находящимися во входном файле 1.txt.

Рис.13. Фрагмент входного файла
3.6. Результаты выполнения программы и их анализ
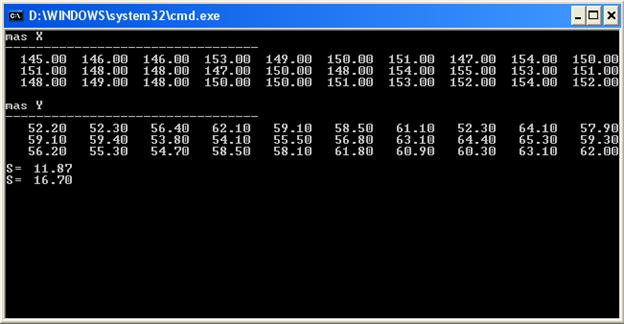
Рис. 14 Фрагмент окна результатов
Сравнительный анализ результатов, полученных в Excel, с результатами, полученных при выполнении программы
Сделаем выводы по результатам полученных данных.
1. Анализ результатов расчетов показывает, что наилучшее уравнение регрессии получается при нахождении коэффициентов по методу наименьших квадратов. Но при очень большом количестве измерений гораздо легче составить корреляционную таблицу и вести расчёты по группированным данным, чем составлять большие циклы нахождения наименьшей суммы квадратов.
2. Сравнивая результаты, полученные при помощи MS Excel и Turbo Pascal, видим, что они совпадают. Это указывает на то, что вычисления верны и отсутствуют какие-либо ошибки.
1)Алексеев В.Е . Вычислительная техника и программирование. Практикум по программированию: Практ. пособие / В.Е. Алексеев, А.С. Ваулин, Г.Б. Петрова: Под. ред. А.В. Петрова. – М.: Высшая школа, 1991.
2)Протосеня А.Г. Малые ЭВМ в горно-экономических задачах: Практ. пособие / А.Г. Протосеня, Б.З. Безмозгин, Г.А. Прудинский. – Л.: Ленинградский горный институт, 1987.
3)Онушкина И.О. Правила оформления курсовых и квалификационных работ: Метод. пособие / И.О. Онушкина, П.Г. Талалай. – СПб: Санкт-Петербургский государственный институт (технический университет), 2005.