| Скачать .docx |
Реферат: Методы решения С1
Ответы на задачи С1:
1) Программа работает неправильно, если a
и b
не равны нулю и имеют разные знаки: в этом случае уравнение ![]() не имеет решений (поскольку модуль – неотрицательная величина), а программа выдаст два решения. Хотя в задании сказано «Приведите пример таких чисел a, b, x,…
», значение x
ни на что не влияет (см. далее), в ответе можно указать любое число x
. Например,
не имеет решений (поскольку модуль – неотрицательная величина), а программа выдаст два решения. Хотя в задании сказано «Приведите пример таких чисел a, b, x,…
», значение x
ни на что не влияет (см. далее), в ответе можно указать любое число x
. Например, ![]()
Лишняя часть программы – ввод x
, поскольку это не исходные данные, а результат. Поэтому вместо оператора
readln(a,b,x);
правильнее написать
readln ( a , b );
Возможная доработка программы – добавить еще один условный оператор, обрабатывающий неучтенный случай (a и b не равны нулю и имеют разные знаки), при котором нет решений:
var a,b,x: real;
begin
readln(a,b);
if a = 0 then
if b = 0 then
write (' любое число ')
else write (' нет решений ')
else
if b = 0 then
write('x = 0')
else
if a*b < 0 then
write('нет решений')
else write('x =',b/a,' или x =',-b/a);
end.
обратите внимание, что для проверки условия «a и b имеют разные знаки» использовано произведение a * b , которое больше нуля, когда два значения имеют одинаковые знаки, и меньше нуля – когда разные
2) Программа работает неправильно, если a
и b
равны нулю: в этом случае решением уравнения ![]() является любое число x
, а программа выдаст только решение
является любое число x
, а программа выдаст только решение ![]() . Хотя в задании сказано «Приведите пример таких чисел a, b, x,…
», значение x
ни на что не влияет (см. далее), в ответе можно указать любое число x
. Например,
. Хотя в задании сказано «Приведите пример таких чисел a, b, x,…
», значение x
ни на что не влияет (см. далее), в ответе можно указать любое число x
. Например, ![]()
Лишняя часть программы – ввод x
, поскольку это не исходные данные, а результат. Поэтому вместо оператора
readln ( a , b , x );
правильнее написать
readln ( a , b );
Возможная доработка программы – добавить еще один условный оператор, обрабатывающий неучтенный случай (a и b равны нулю), при котором решением является любое число:
var a,b,x: real;
begin
readln(a,b);
if b = 0 then
if a = 0 then
write('любое число')
else write('x = 0')
else
if a = 0 then
write('нет решений')
else write('x =',-b/a);
end.
можно еще немного оптимизировать программу: заметим, что в обеих частях первого условного оператора встречается оператор if a = 0 then ; его можно «вынести» наверх, сделать внешним, а не вложенным:
if a = 0 then
if b = 0 then
write ('любое число')
else write ('нет решений')
else
write('x=',-b/a);
если вы боитесь запутаться во вложенных условных операторах, можно использовать сложные условия и рассмотреть три возможных варианта (важно не забыть ни один!):
if (a=0) and (b=0)then
write(' любое число ');
if (a=0) and (b<>0)then
write(' нет решений ');
if a <> 0 then
write('x=',-b/a);
здесь нужно убедиться, что для каждого варианта входных данных сработает один и только один условный оператор
3)  Согласно условию, нас интересует область, закрашенная на рисунке серым цветом. Если рассмотреть границы области по осям координат, получим четыре условия:
Согласно условию, нас интересует область, закрашенная на рисунке серым цветом. Если рассмотреть границы области по осям координат, получим четыре условия:
по оси X: ![]()
по оси Y: ![]()
В программе не учитывается условие ![]() , причем оно не перекрывается другими условиями. Поэтому программа работает неправильно в том случае, когда
, причем оно не перекрывается другими условиями. Поэтому программа работает неправильно в том случае, когда ![]() и
и ![]() (область красного цвета на рисунке). Одна из таких точек:
(область красного цвета на рисунке). Одна из таких точек: ![]()
Для доработки программы нужно добавить еще один условный оператор с недостающим условием и соответствующий ему else
-блок, выдающий сообщение в случае невыполнения этого условия:
var x 0, у0, у: real ;
begin
readln (x0, y0);
if (x0 < 2)then begin
if (x0 > 0)then begin
if (y0 > 0)then begin
у = 2 – х0;
if ( y 0 < у) then
writeln ('точка лежит внутри области')
else writein ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
end .
Это решение работает, но громоздко и некрасиво. Заметим, что два условия ![]() и
и ![]() автоматически обеспечивают выполнение условия
автоматически обеспечивают выполнение условия ![]() , которое становится лишним:
, которое становится лишним:
if (x0 > 0)then begin
if (y0 > 0)then begin
у = 2 – х0;
if ( y 0 < у) then
writeln ('точка лежит внутри области')
else writein ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
Сделаем еще один шаг: попадание точки в заданную область равносильно одновременному выполнению (операция «И») трех условий: ![]() ,
, ![]() и
и ![]() , поэтому получаем такой вариант с использованием сложного условия:
, поэтому получаем такой вариант с использованием сложного условия:
if (x0 > 0) and (y0 > 0) and (y0 < 2 - x0) then begin
writeln ('точка лежит внутри области')
else writein ('точка не лежит внутри области');
4) В этой программе внешне все выглядит правильно, поэтому весьма вероятно, что сделана «ловушка» на какой-то особый (вырожденный) случай. При решении квадратного уравнения «особый случай» – это равенство дискриминанта нулю (два одинаковых корня). Проверяя его, сразу обнаруживаем, что при этом условие D
>
0
не срабатывает и программа выдает сообщение «действительных корней нет». Поэтому, например, для ![]() программа работает неверно. При этом можно вводить любые x
1
и x
2
, поскольку в эти переменные записываются результаты вычислений (корни уравнения) анне исходные данные. Это ответ на второй вопрос: вместо оператора
программа работает неверно. При этом можно вводить любые x
1
и x
2
, поскольку в эти переменные записываются результаты вычислений (корни уравнения) анне исходные данные. Это ответ на второй вопрос: вместо оператора
readln(a,b,c,x1,x2);
правильнее написать
readln ( a , b , c );
Чтобы исправить программу, достаточно вместо условия D > 0 написать D >= 0 :
var a, b, с , D, xl, x2: real;
begin
readln(a, b, с);
D := b*b - 4*a*c;
if D >= 0 then begin
xl := (-b + sqrt(D))/(2*a);
x2 := (-b - sqrt(D))/(2*a);
write('xl =', xl);
write('x2 =', x2);
end
else writeln ('действительных корней нет');
end .
5) Программа очень плохо написана, мысль автора слабо прослеживается, поэтому сложно разбираться в коде. Для проверки четности числа используется операция mod
–остаток от деления целых чисел. Очевидно, что если остаток от деления a на 2 (записывается a mod 2
) – нуль, то число a
делится на 2 без остатка, то есть – четное.
Для того, чтобы выяснить, когда программа будет работать неверно, можно использовать ручную прокрутку для четырех возможных вариантов:
1. оба числа четных
2. a – четное, b – нечетное
3. a – нечетное, b – четное
4. оба числа нечетных
При этом обнаруживаем, что программа неверно работает во втором случае, например, для ![]() . Простейшая (?) доработка программы с сохранением замысла (?) автора может быть такая (расширено действие условного оператора и добавлен else
-блок)
. Простейшая (?) доработка программы с сохранением замысла (?) автора может быть такая (расширено действие условного оператора и добавлен else
-блок)
var a, b: integer;
begin
readln(a, b);
a := a mod 2;
if a > 0 then begin
b := b mod 2;
if b > 0 then
writeln ('четных чисел нет')
else writeln ('четное число есть');
end
else writeln ('четное число есть');
end .
Чтобы сделать программу красивой и понятной, запишем на Паскале вполне ясное условие: «если a – четное или b – четное, то четное число есть, иначе – нет»:
var a, b: integer;
begin
readln(a, b);
if (a mod 2 = 0) or (b mod 2 = 0) then
writeln ('четное число есть')
else writeln ('четных чисел нет')
end.
6) Вспомним, что треугольник можно построить, если длина каждой стороны меньше суммы длин двух оставшихся, это условие нужно проверить для все трех сторон. Анализируя программу, можно понять, что она не выдает на экран никакого сообщения, если условие в первом условном операторе верно (x
+
y
>
z
), а в одном из других – неверно, например, для случая ![]() (треугольник построить нельзя). Чтобы заставить ее работать правильно, достаточно добавить два else-блока для внутренних условных операторов:
(треугольник построить нельзя). Чтобы заставить ее работать правильно, достаточно добавить два else-блока для внутренних условных операторов:
var х, у, z : real ;
begin
readln (x, у, z);
if (x + y > z) then begin
if (x + z > y) then
if (y + z > x) then
writeln ('треугольник построить можно')
else writeln ('треугольник построить нельзя')
else writeln ('треугольник построить нельзя');
end
else writeln ('треугольник построить нельзя');
end.
Чтобы сделать программу красивой и понятной, нужно понять, что треугольник можно построить только в случае одновременного выполнения всех трех условий; в программе
их нужно связать операцией and («И»):
var х, у, z : real ;
begin
readln (x, у, z);
if (x + y > z) and (x + z > y) and (y + z > x) then
writeln ('треугольник построить можно')
else writeln ('треугольник построить нельзя');
end.
7) В программе неявно предполагается, что r
1
>
r
2
, хотя по условию это не всегда так. Поэтому она будет выдавать неверный ответ, когда r
2
>
r
1
и полученное расстояние h
(от точки до начала координат) удовлетворяет условию r
1
<
h
<
r
2
, например, для ![]() .
.
Простейший способ доработать программу – добавить еще один условный оператор со сложным условием, обрабатывающий случай r
2
>
r
1
:
var x, у, rl,r2:real;
h: real;
begin
readln (x, у, rl, r2);
h:= sqrt (x*x + y*y);
if (h < rl) AND (h > r2) then
writeln ('точка А лежит внутри кольца');
if (h < r2) AND (h > r1) then
writeln ('точка А лежит внутри кольца');
end .
Более красивый способ – объединить два сложных условия в одно с помощью операции or («ИЛИ»), поскольку и в том, и в другом случае выдается одинаковое сообщение:
var x, у, rl,r2:real;
h: real;
begin
readln (x, у, rl, r2);
h := sqrt(x*x + y*y);
if (h < rl) AND (h > r2) OR (h < r2) AND (h > r1) then
writeln ('точка А лежит внутри кольца');
end .
Обратите внимание на то, что операция OR имеет более низкий приоритет, чем AND , поэтому в этом сложном условии она будет выполняться последней, как и требуется.
Остается ответить на третий вопрос: как можно обойтись без операций AND или OR . Конечно, возможен «лобовой» вариант, использующий вложенные условные операторы:
if h < rl then
if h > r 2 then
writeln ('точка А лежит внутри кольца');
if h > rl then
if h < r2 then
writeln ('точка А лежит внутри кольца');
Обратите внимание, что нам понадобилось отдельно «обойти» случай h = r1 , потому что по условию понятие «внутри кольца» рассматривается в строгом смысле и при h = r1 считается, что точка не попадает в кольцо.
Для более грамотного решения задачи нужно попробовать использовать арифметические операции, так чтобы результат вычисления некоторого выражения прямо отвечал на нужный вопрос. Поскольку числа могут быть самые разные, лучше «играть» не на конкретных значениях, а на знаке, то есть, если точка находится внутри кольца, выражение должно быть, скажем, отрицательным, а если нет – то положительным. Или наоборот.
Если точка находится внутри кольца, то находится h между r1 и r2 . Это значит, что разности h - r 1 и h - r 2 имеют разный знак, следовательно, их произведение отрицательно[1] . Таким образом, красиво написанная программа может иметь, например, такой вид:
var x, у, rl,r2:real;
h: real;
begin
readln (x, у, rl, r2);
h := sqrt(x*x + y*y);
if (h - rl)*(h - r2) < 0 then
writeln ('точка А лежит внутри кольца');
end.
8) Во-первых, заметим, что в программе проверяются три условия, а заданы – четыре. Сразу находим, что условие y0
>
-2
«выпало». Поэтому, например, программа ошибочно сообщит, что точка с координатами ![]() находится внутри области (в самом деле – нет).
находится внутри области (в самом деле – нет).
Кроме того, если условие в первом условном операторе истинно, а одно из последующих – ложно, программа вообще не выдает сообщения на экран, это неверно. Таким образом, для входных данных ![]() или
или ![]() программа также работает неверно.
программа также работает неверно.
Чтобы исправить эти ошибки «в лоб», можно добавить еще один условный оператор, проверяющий недостающее условие y0 > -2 , и добавить else -блоки, чтобы выводить сообщение «не лежит внутри области» при нарушении любого из условий:
var x0, y0: real;
begin
readln (x0, y0)
if(x0 < 2)then begin
if(x0 > -2)then
if (y0 < 2) then
if (y0 > -2) then
writeln ('точка лежит внутри области')
else writeln ('точка не лежит внутри области')
else writeln ('точка не лежит внутри области');
end
else writeln ('точка не лежит внутри области');
end .
чтобы сделать красивую программу, нужно перевести на Паскаль сложное условие «точка лежит внутри области, если одновременно выполняются четыре условия…»; слова «одновременно выполняются» говорят о том, что нужно использовать логическую операцию and («И»):
var x0, y0: real;
begin
readln (x0, y0)
if (x0 < 2) and (x0 > -2) and
(y0 < 2) and (y0 > -2) then
writeln ('точка лежит внутри области')
else writeln ('точка не лежит внутри области');
end .
| 8 |
||||||||
| 7 |
||||||||
| 6 |
||||||||
| 5 |
||||||||
| 4 |
||||||||
| 3 |
||||||||
| 2 |
||||||||
|
|
|
1 |
||||||
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9) Легко проверить, что клетка (i=5,j=4 ) удовлетворяет условию i =9- j , и, следовательно, сложному условию ( i =9- j ) OR ( i = j ) (OR означает логическую операцию «ИЛИ» - выполнение хотя бы одного из двух условий)
Для ответа на остальные вопросы нарисуем поле и расставим королей (в самом деле в этой задаче все равно, какого цвета поля, поэтому мы их не раскрашивали).
Короли могут ходить по диагонали, поэтому чтобы дойти до поля ( i , j ) , королю лучше
сначала идти по диагонали, чтобы быстрее выйти на нужную горизонталь или вертикаль, а затем двигаться по этой горизонтали (или вертикали) к заданной клетке.
· черный король [его координаты (1,1)] идет по диагонали k -1 шагов, где k = min ( i , j ) до клетки с координатами ( i , i ) (если i <= j ) или до клетки ( j , j ) (если i >= j ); затем он делает оставшееся количество шагов, max ( i , j )- k , по горизонтали или вертикали, так что его общее число шагов равно
max(i,j)-1
· аналогично белый король [его координаты (8,1)] идет по диагонали q -1 шагов, где q = min (9- i , j ) до клетки с координатами (9- i ,9- i ) (если 9- i <= j ) или до клетки ( j , j ) (если 9- i >= j ); затем он делает оставшееся количество шагов, max (9- i , j )- q , по горизонтали или вертикали, так что его общее число шагов равно
max(9-i,j)-1
· таким образом, нас интересуют клетки ( i , j ) , для которых
max(i,j)-1= max(9-i,j)-1 или max(i,j)= max(9-i,j) (*)
(1,8) |
(2,8) |
8 |
||||||
| (1,7) |
7 |
|||||||
| (8,6) |
6 |
|||||||
| (5,5) |
5 |
|||||||
| 4 |
||||||||
| 3 |
||||||||
| 2 |
||||||||
|
|
|
1 |
||||||
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Чтобы найти все пары ( i , j ) , для которых верно полученное равенство, рассмотрим сначала левую половину доски (i<=4):
· если i <=4 , то 9- i >=5> i , поэтому равенство (*) справедливо только при j >=9- i ; это область выше главной диагонали и на ней;
· в силу симметрии сразу можно построить соответствующую область и в правой части доски (см. рисунок справа):
Из указанных полей только три, выделенные желтым маркером, оказываются внутри нужной области
(i=1,
j=8
), (i=2,
j=8
), (i=1,
j=7),
(i=5,
j=5
), (i=8,
j=6)
Правильное условие, определяющее нужную область, выглядит так: «клетка выше главной диагонали (или на ней) и одновременно выше второй диагонали (или на ней)». Остается записать его на Паскале:
( j >= i ) and ( j >=9- i )
Доработка программы сводится просто к замене условия, все остальное правильно.
10) Попробуем прежде всего найти математическое решение неравенства ![]() . Оно истинно, если числитель и знаменатель дроби имеют один знак, или оба положительные, или оба отрицательные. При
. Оно истинно, если числитель и знаменатель дроби имеют один знак, или оба положительные, или оба отрицательные. При ![]() получаем:
получаем:
(![]() и
и ![]() ) или (
) или (![]() и
и ![]() )
)
В краткой форме: ![]() или
или ![]() . В зависимости от значения
. В зависимости от значения ![]() получаем
получаем
Случай 1
. При ![]() и
и ![]() :
: ![]() или
или ![]()
Случай 2
. При ![]() и
и ![]() :
: ![]() или
или ![]()
Теперь рассмотрим случай ![]() . Снова получаем два варианта:
. Снова получаем два варианта:
(![]() и
и ![]() ) или (
) или (![]() и
и ![]() )
)
При ![]() всегда ложно выражение в первых скобках, а при
всегда ложно выражение в первых скобках, а при ![]() – выражение во вторых скобках. Поэтому можно записать еще два случая через двойные неравенства:
– выражение во вторых скобках. Поэтому можно записать еще два случая через двойные неравенства:
Случай 3
. При ![]() и
и ![]() :
: ![]()
Случай 4
. При ![]() и
и ![]() :
: ![]()
Запишем основную часть программы, определив принадлежность каждого else -блока и используя запись «лесенкой»:
if b > 0 then
write('x > ', a, ' или x < 0')
else
if a > 0 then
write('0 < x < ', a)
else
write(a, ' < x < 0');
Анализ условных операторов показывает, что неправильно обрабатывается Случай 2
(![]() и
и ![]() ), то есть, в качестве примера можно привести пару
), то есть, в качестве примера можно привести пару ![]() при любом
при любом ![]() (которое вообще не влияет на результат).
(которое вообще не влияет на результат).
В программе вводится переменная ![]() , которая нигде не используется. Поэтому это – лишняя часть
программы, можно убрать
, которая нигде не используется. Поэтому это – лишняя часть
программы, можно убрать ![]() из списка объявляемых переменных и списка ввода в операторе readln
.
из списка объявляемых переменных и списка ввода в операторе readln
.
Простейший и (в данной задаче) наиболее логичный вариант доработки программы – добавить еще один условный оператор для правильного разделения Случая 1 и Случая 2 :
var a, b: real;
begin
readln(a, b);
if b > 0 then
if a > 0 then
write('x > ', a, ' или x < 0')
else
write('x < ', a, ' или x > 0')
else
if a > 0 then
write('0 < x < ', a)
else
write(a, ' < x < 0');
end .
11)  Первое условие в программе, x
*
x
+
y
*
y
>=
4
, означает «вне круга». Если выполняются одновременно второе и третье условия, x
<=
2
и y
<=
x
, точка находится в секторе
между прямыми
Первое условие в программе, x
*
x
+
y
*
y
>=
4
, означает «вне круга». Если выполняются одновременно второе и третье условия, x
<=
2
и y
<=
x
, точка находится в секторе
между прямыми ![]() и
и ![]() , в который входит заштрихованная область. Таким образом, выполнение всех трех условия означает «вне круга и в секторе». Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Поэтому для любой точки в «красной зоне», например, для точки (1; –2), программа выдаст неправильный ответ «принадлежит».
, в который входит заштрихованная область. Таким образом, выполнение всех трех условия означает «вне круга и в секторе». Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Поэтому для любой точки в «красной зоне», например, для точки (1; –2), программа выдаст неправильный ответ «принадлежит».
Если записать программу «лесенкой», становится видна еще одна ошибка.
if x*x+y*y >= 4 then
if x <= 2 then
 if y
<=
x then
if y
<=
x then
write ('принадлежит')
else
write ('не принадлежит')
Дело в том, что любой else относится к ближайшему if , поэтому сообщение «не принадлежит» выводится только тогда, когда первые два условия выполняются, а третье – нет. Следовательно, для точки (0;0), например, программа вообще не выдаст никакого сообщения (первое условие ложно).
Чтобы исправить программу, можно добавить еще одно условие y >= 0 (это отсекает «красную зону») и объединить все четыре условия в одно сложное условие:
var x,y: real;
begin
readln(x,y);
if (x*x+y*y >= 4) and (x <= 2) and
(y <= x) and (y >= 0) then
write('принадлежит')
else
write ('не принадлежит')
end .
12) 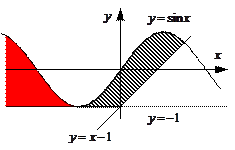 Записанные в программе условия означают «ниже синусоиды» и в секторе
между прямыми
Записанные в программе условия означают «ниже синусоиды» и в секторе
между прямыми ![]() и
и ![]() , в который входит заштрихованная область. Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Первое пересечение синусоиды с осью абсцисс происходит при
, в который входит заштрихованная область. Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Первое пересечение синусоиды с осью абсцисс происходит при ![]() , поэтому программа выдает неверный ответ «принадлежит», например, для точки (-4;0), которая в самом деле не принадлежит заштрихованной области.
, поэтому программа выдает неверный ответ «принадлежит», например, для точки (-4;0), которая в самом деле не принадлежит заштрихованной области.
Если записать программу «лесенкой», становится видна еще одна ошибка.
if y >= -1 then
if y <= sin(x) then
 if y
>=
x-1 then
if y
>=
x-1 then
write ('принадлежит')
else
write ('не принадлежит')
Дело в том, что любой else относится к ближайшему if , поэтому сообщение «не принадлежит» выводится только тогда, когда первые два условия выполняются, а третье – нет. Следовательно, для точки (0;-2), например, программа вообще не выдаст никакого сообщения (первое условие ложно).
Чтобы исправить программу, можно добавить еще одно условие x >= - pi /2 (это отсекает «красную зону») и объединить все четыре условия в одно сложное условие:
var x,y: real;
begin
readln(x,y);
if (y >= -1) and (y <= sin(x)) and
(y >= x-1) and (x >= -pi/2) then
write('принадлежит')
else
write ('не принадлежит')
end .
13) 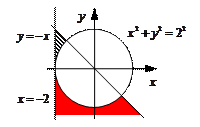 Эта задача полностью аналогична задаче 11 (рисунки симметричны). Вот основная часть программы с выделенной структурой:
Эта задача полностью аналогична задаче 11 (рисунки симметричны). Вот основная часть программы с выделенной структурой:
if x*x+y*y >= 4 then
if x >= -2 then
 if y
<=
-
x then
if y
<=
-
x then
write(' принадлежит ')
else
write(' не принадлежит ')
Для точек в «красной зоне» (см. рисунок) программа ошибочно выдает ответ «принадлежит», а для точек, в которых не выполняется первое или второе условие (внутри круга или слева от прямой ![]() ) вообще не выдается никакого сообщения.
) вообще не выдается никакого сообщения.
Чтобы исправить программу, можно добавить еще одно условие y >= 0 (это отсекает «красную зону») и объединить все четыре условия в одно сложное условие:
var x,y: real;
begin
readln(x,y);
if (x*x+y*y >= 4) and (x >= -2) and
(y <= -x) and (y >= 0) then
write('принадлежит')
else
write ('не принадлежит')
end .
14) Условный оператор
if a > b then begin x:=a; a:=b; b:=x; end;
упорядочивает переменные a и b с помощью вспомогательной переменной x , записывая в переменную a минимальное из двух значений а в переменную b – максимальное. Аналогично оператор
if b > c then begin x:=b; b:=c; c:=x; end;
упорядочивает значения b и с .
Очевидно, что x используется только как вспомогательная переменная, поэтому вводить ее с клавиатуры не нужно, оператор ввода должен выглядеть так:
read ( a , b , c );
Программа работает неправильно, если минимальное число вводится последним и попадает в переменную c . Действительно, выполняя программу для a=3 , b=2 и c=1 получаем
|
|
a |
b |
c |
| readln(a, b, c, x); |
3 |
2 |
1 |
| if a > b then begin x:=a; a:=b; b:=x; end; |
2 |
3 |
1 |
| if b > c then begin x:=b; b:=c; c:=x; end; |
2 |
1 |
3 |
Чтобы исправить ошибку, в конец программы нужно добавить строчку, упорядочивающую a и b (точную копию первого условного оператора). Вот исправленная программа
var a, b, c, x: integer;
begin
read(a, b, c);
if a > b then begin x:=a; a:=b; b:=x; end;
if b > c then begin x:=b; b:=c; c:=x; end;
if a > b then begin x:=a; a:=b; b:=x; end;
write(a,b,c);
end.
15) В приведенной программе две ошибки. Во-первых, условия
y <= sin ( x )
y <= 0.5
y >= 0
выделяют не только заштрихованную область, но и аналогичные области в каждой полуволне (на рисунке они обозанчены красным цветом).

Например, для точки ![]() программа ошибочно выдаст ответ «принадлежит». Поэтому нужны два дополнительных ограничения по координате x
(для заданной области –
программа ошибочно выдаст ответ «принадлежит». Поэтому нужны два дополнительных ограничения по координате x
(для заданной области – ![]() ):
):
x <= pi ( или, например, x <= 4)
x >= 0
Во-вторых, записав программу «лесенкой» с выделением структуры
if y <= sin(x) then
if y <= 0.5 then
if y >= 0 then
write('принадлежит')
else
write ('не принадлежит');
мы видим, что else
-блок относится только к последнему условному оператору, поэтому сообщение «не принадлежит» не будет выведено, если одно из первых двух условий ложно. Поэтому, например, для точки ![]() программа не выдаст вообще никакого ответа, то есть, сработает неверно.
программа не выдаст вообще никакого ответа, то есть, сработает неверно.
Самый простой способ доработки программы – использовать одно сложное условие, определяющее именно заштрихованную область (с ограничением по оси x )
var x, y: real;
begin
readln(x, y);
if (y <= sin(x)) and (y <= 0.5) and (y >= 0) and
(x >= 0) and (x <= pi) then
write('принадлежит')
else
write ('не принадлежит');
end .
[1] Аналогичная ситуация возникает при решении уравнения методом деления отрезка пополам (кто помнит :-).