Реферат: Программа решения трансцендентного уравнения на языке Pascal

Министерство науки и образования РТ

Казанский Государственный Технический Университет

имени А.Н. Туполева

Отчёт

по расчетно-графической работ e

Выполнил студент гр. 3108

Сабиров Ленар

Принял: Балоев. А.А.

Казань 2009 г

Задания

1. Решение трансцендентного уравнения.

Решить уравнение методом Ньютона

2. Вычисление определённого интеграла

Вычислить интеграл 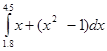методом трапеции.

Задание 1. Решение трансцендентного уравнения.

Решить уравнение методом Ньютона

Решение:

1. Решение трансцендентного уравнения методом Ньютона.

1.1 Дано уравнение

(1)

1.2 Обозначим правую часть уравнения (1) через функцию:

(2)

1.3 Определим область решения уравнения. исследуем функцию для определения интервала на оси х, где функция обращается в ноль.

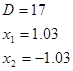
-1.03 1.03

1.4 Отсюда видно что x будет принимать отрицательные значения от -1.03 до 1.03

Построим график этой функции

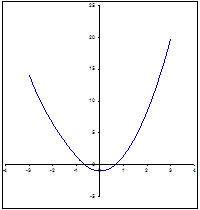
Рис 1

Блок-схема алгоритма решения

На Рис. 2 приведена блок-схема алгоритма решения задачи.

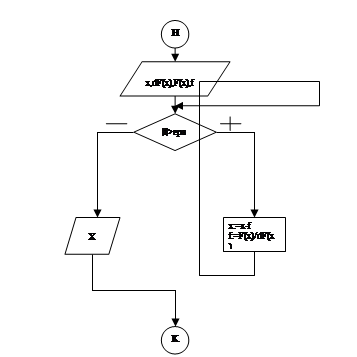
Рис 2

Программа решения задачи на языке Pascal

program Nuton ;

{$ N +}

uses crt ;

var x , x1,eps,pf:extended;

i:integer;

function f(x:real):real;

begin

f:=x+2*(sqr(x)-1)+exp(-sin(x));

end;

function df(x:real):real;

begin

df:=1+4*x+exp(-sin(x))*(-cos(x));

end ;

begin

clrscr ;

write ('приближенное значение корня = ');

readln ( x 1);

write ('необходимая точность = ');

readln(eps);

x:=x1;

pf:=f(x)/df(x);

i:=0;

while abs(pf)>eps do

begin

x:=x-pf;

pf:=f(x)/df(x);

inc(i);

{writeln(x:1:4, pf:10:4);}

end ;

writeln ('точное значение корня = ', x :1:4);

writeln ('количество итераций = ', i );

readkay ;

Результат решения задачи

На рисунке 3 представлен результат решения задачи

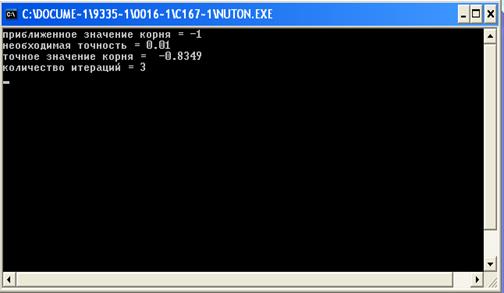
Рис 3

Задание 2

Решение:

Построим график функции

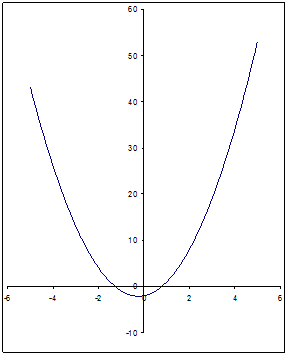
Рис 4

Вычислим значение интеграла:

Блок схема алгоритма решения

На Рис 5 приведена блок схема алгоритма вычисления определённого интеграла по методу трапеций

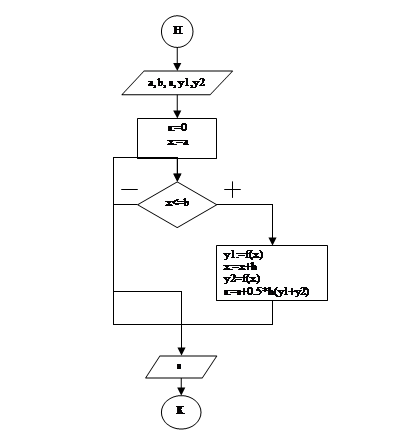
Программа вычисления интеграла на языке Pascal

program variant8;

var n,y1,y2,a,b,h,x,k,s:real;

function f(x:real):real;

begin

f:=x+2*(sqr(x)-1)

end;

begin

write('a- нижний предел интегрирования :'); readln(a);

write('b- верхний предел интегрирования :'); readln(b);

write (' h -шаг интегрирования:'); read ( h );

x:=a;

while x<=b do begin

y1:=f(x);

x:=x+h;

y2:=f(x);

s:=s+0.5*h*(y1+y2);

end;

writeln('s=',s:10:5);

end.

Результат вычисления интеграла

1.5 На Рис5 и 6 представлен результат вычисления интеграла и погрешности его вычисления

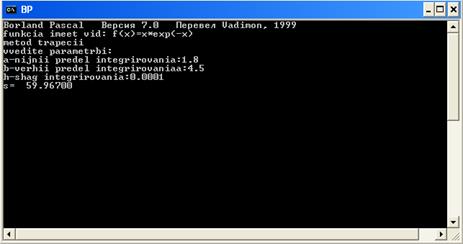
Рис 5

Рис 6