| Скачать .docx |
Реферат: Подготовка электронных документов в MS Word 2

НОУ ВПО ТУЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И БИЗНЕСА
им. Н. Д. Демидова
ОТЧЕТ
о выполнении компьютерного практикума по дисциплине “Информатика”
“Подготовка электронных документов в MS Word”
Выполнила ст. гр. ЭУН-10 Кондратьева Ю. Г.
Проверил доц. Ильин Р. А.
Тула- 2011
СОДЕРЖАНИЕ
ВВЕДЕНИЕ………………………………………………………………..………3
1. РАЗРАБОТКА АЛГОРИТМА (ВАРИАНТ №3)………………..……….3
2. ГРАФИК ФУНКЦИИ (ВАРИАНТ №4)……………………….…….……4
3. ПОСТРОЕНИЕ ДИАГРАММЫ (ВАРИАНТ №5)……………….…….5
4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (ВАРИАНТ №6)…….…………………….……………..6
4.1. Решение СЛАУ на основе линейной алгебры…………...……………7
4.2. Решение СЛАУ, используя метод "Поиск решения…" (пункт главного меню" Сервис") MS Exel………………………….………..11
4.3. Решение СЛАУ методом Крамера (метод определителей)………..14
ЗАКЛЮЧЕНИЕ……………………………………………..………………..20
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ…………………………….20
ВВЕДЕНИЕ
Дисциплина "Информатика" имеет важное значение при подготовке специалистов высшего профессионального образования по любому направлению[1], поскольку сегодня в любой сфере деятельности человека необходимо:
1) иметь навыки подготовки документов (в первую очередь электронных) в сфере профессиональной деятельности;
2) обладать знаниями использования современных информационных систем и технологий при решении профессиональных задач;
3) уметь реализовывать обмен информации с коллегами организациями на основе вычислительных сетей и телекоммуникаций.
Основная цель компьютерного практика по дисциплине "Информатика" заключается в получении и закреплении навыков подготовки пояснительных записок (ПЗ):
· к контрольным работам;
· рефератам;
· курсовым работам (КР) и проектам (КП);
· выпускным квалификационным работам (ВКР);
Практикум состоит из выполнения заданий четырех видов:
· разработки схемы алгоритма решения конкретной задачи;
· построения графика с элементами вычисления функции;
· построения диаграммы, отражающей изменение состояния процесса (объекта);
· решение системы линейных алгебраических уравнений.
Каждому студенту выдаются номера вариантов по каждому из четырех заданий. Конкретные задания и их выполнение представлены ниже.
1. РАЗРАБОТКА АЛГОРИТМА (ВАРИАНТ № 3)
Задание
. Разработать алгоритм произведения двух полиномов ![]() степени m
и
степени m
и ![]() степени n
.
степени n
.
Решение . Вопросы разработки схем алгоритмов различных задач подробно рассмотрены в учебном пособии [1]. Схема алгоритма представлена на рис. 1.1.
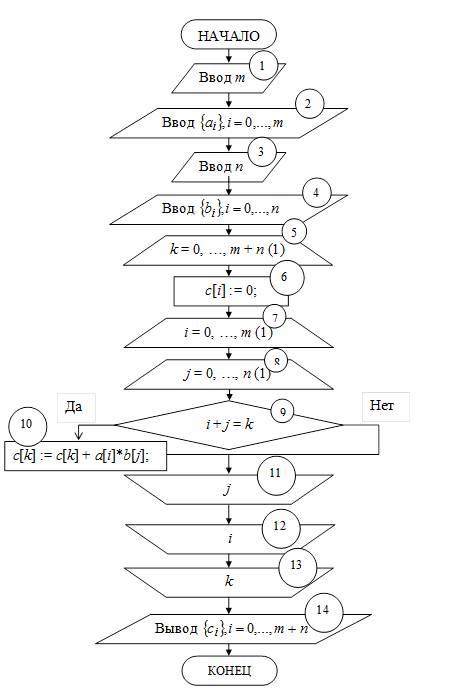
Рис. 1.1. Умножение полиномов. Схема алгоритма
Введем обозначения
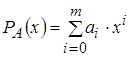 – первый полином множитель степени m
;
– первый полином множитель степени m
;
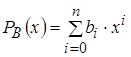 – второй полином множитель степени n
;
– второй полином множитель степени n
;
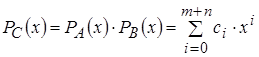 – произведение полиномов степени
– произведение полиномов степени
m
+ n
.
Блоки 1 – 4 алгоритма реализуют ввод коэффициентов полиномов множителей. Коэффициенты произведения полиномов ![]() формируются в трех вложенных циклах (блоки 5 – 13). Блок 14 реализует вывод коэффициентов
формируются в трех вложенных циклах (блоки 5 – 13). Блок 14 реализует вывод коэффициентов ![]() произведения полиномов.
произведения полиномов.
2. ГРАФИК ФУНКЦИИ (ВАРИАНТ № 4)
Задание
. Построить график функции ![]() ,
, ![]() .
.
Решение . Вопросы построения различных графиков подробно рассмотрены в работе [3] и на консультации. Данные для построения графика функции представлены в табл. 2.1.
Таблица 2.1
Исходные данные для построения графика
| 1 | 1,2 | 1,4 | 1,6 | 1,8 | 2 | 2,2 | 2,4 | 2,6 | 2,8 | 3 | |
| 0,00 | 0,36 | 0,64 | 0,84 | 0,96 | 1,00 | 0,96 | 0,84 | 0,64 | 0,36 | 0,00 |
Во второй строке табл. 2.1 значения функции ![]() вычисляются по формуле, например, для x
= 1 значение
вычисляются по формуле, например, для x
= 1 значение ![]() вычисляется по формуле
вычисляется по формуле
=-(B1-1)*(B1-3), для x
= 1,2 – =-(C1-1)*(C1-3) и т.д.
На рис. 2.1 представлен график функции ![]() .
.
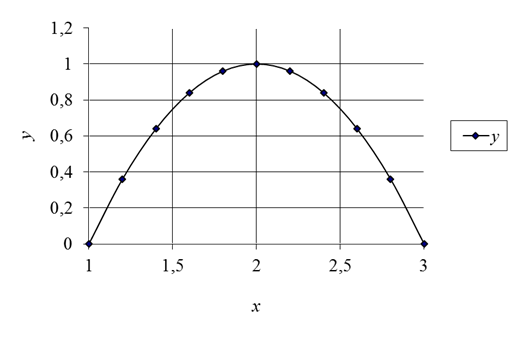
Рис. 2.1. График функции ![]()
График представляет собой параболу второго порядка с максимумом в точке ![]() = 2;
= 2; ![]() .
.
3.ПОСТРОЕНИЕ ДИАГРАММЫ (ВАРИАНТ № 5)
Задание . Требуется построить круговую диаграмму посещаемости студентами группы консультаций по дисциплине “Информатика”.
Решение . Вопросы построения различных диаграмм подробно рассмотрены в работе [3] и на консультации. Посещаемость студентами группы консультаций по дисциплине “Информатика” приведены в табл. 3.1.
Таблица 3.1
Посещаемость студентами группы консультаций по дисциплине “Информатика”
| № п/п |
Дата Ф.И.О. студента |
27.12 | 10.01 | 16.01 | 23.01 | 30.01 | Кол-во посещ. |
| 1. | Абрамов А.С. | -[1] | - | +[2] | + | + | 3 |
| 2. | Борисов М.К. | + | - | + | + | + | 4 |
| 3. | Дуремар А.И. | + | + | + | + | + | 5 |
| 4. | Иванов И.И. | + | + | + | - | + | 4 |
| 5. | Кудеярова М.П. | + | + | - | + | + | 4 |
| 6. | Макарова Е.А. | + | + | + | + | + | 5 |
| 7. | Иванова Е.Ф. | + | + | - | + | + | 4 |
| 8. | Сидоров С.С. | + | + | + | + | + | 5 |
| 9. | Федоров А.Я. | + | + | - | + | + | 4 |
| 10. | Яковлева А.Ф. | + | - | - | - | + | 2 |
| ИТОГО: | 40 | ||||||
Максимально возможное количество посещений занятий студентами равно 10 (студентов) × 5 (занятий) = 50.
% посещаемости = ![]() = 80 %.
= 80 %.
% прогулов = 100 % - 80 % = 20 %.
Круговая диаграмма посещаемости студентами группы консультаций по дисциплине “Информатика” на рис. 3.1.
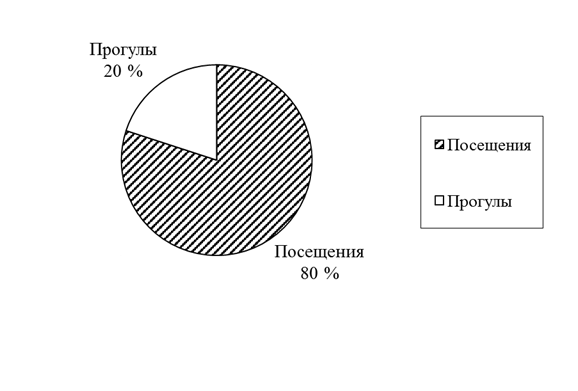
Рис. 3.1. Круговая диаграмма посещаемости студентами группы консультаций по дисциплине “Информатика”
Рис. 3.1 показывает, что посещаемость занятий студентами составляет 80 %.
4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (ВАРИАНТ № 6)
Задание . Требуется решить систему линейных алгебраических уравнений (СЛАУ)
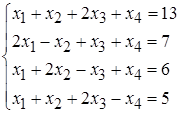 .
.
Решение . Рассмотрим три метода решения СЛАУ и информационные технологии реализации этих методов на основе табличного процессора MSExcel, входящего в состав интегрированного пакета прикладных программ Microsoft Office, представленные в учебном пособии [2]:
- решение СЛАУ на основе методов линейной алгебры;
- решение СЛАУ, используя метод "Поиск решения..." (пункт главного меню "Сервис") MSExcel;
- решение СЛАУ методом Крамера (методом определителей).
4.1. Решение СЛАУ на основе методов линейной алгебры
В терминах линейной алгебры СЛАУ записывается следующим образом:
![]() , (4.1)
, (4.1)
где A – матрица коэффициентов СЛАУ ;
B – вектор свободных членов СЛАУ;
X – вектор решения СЛАУ.
Домножив слева левую и правую части выражения (4.1) на матрицу, обратную матрице коэффициентов СЛАУ, получим
![]() . (4.2)
. (4.2)
Учитывая, что ![]() (где I
– единичная матрица), а
(где I
– единичная матрица), а ![]() , получим выражение для поиска вектора решения
, получим выражение для поиска вектора решения
![]() . (4.3)
. (4.3)
Значит, для получения вектора решения СЛАУ X необходимо получить матрицу, обратную матрице коэффициентов СЛАУ, и умножить ее на вектор свободных членов СЛАУ B . Для обращения квадратной матрицы в MSExcel существует функция =МОБР(левый_верхний_элемент_исходной_матрицы: правый_нижний_элемент_исходной_матрицы). Для умножения обратной матрицы коэффициентов СЛАУ на вектор свободных членов воспользуемся функцией =МУМНОЖ(левый_верхний_элемент_исходной_матрицы: правый_нижний_элемент_исходной_матрицы;верхний_элемент_вектора: нижний_элемент_вектора). Решение СЛАУ из четырех уравнений на основе методов линейной алгебры в MSExcel, входящего в состав интегрированного пакета MicrosoftOffice 2003 представлено на рис. 4.1.
В строках с 1 по 25 представлено условие задачи и принятые обозначения. В ячейках (B
27:E
30) реализуется функция обращения матрицы коэффициентов СЛАУ с помощью функции =МОБР(B
10:E
13). Функцию обращения матрицы возможно создать, используя мастер формул. Для этого необходимо выделить ячейки (B
27:E
30) и щелкнуть по пиктограмме MSExcel![]() , за тем в группе “Математические” выбрать функцию МОБР и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора мышь) элементы исходной матрицы коэффициентов СЛАУ (ячейки (B
10:E
13)) и нажать кнопку “OK”.
, за тем в группе “Математические” выбрать функцию МОБР и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора мышь) элементы исходной матрицы коэффициентов СЛАУ (ячейки (B
10:E
13)) и нажать кнопку “OK”.
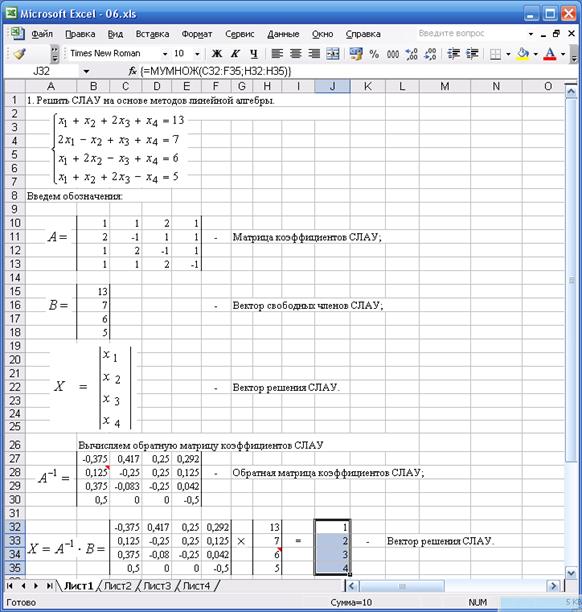
Рис. 4.1. Решение СЛАУ на основе методов линейной алгебры
При закрытии окна “Аргументы функции” в выделенной области (ячейках (B 27:E 30)) для обратной матрицы сформируется только первый элемент в первой строке. Для формирования остальных элементов обратной матрицы следует нажать клавишу F 2, а за тем при одновременно нажатых клавишах Shift и Ctrl нажать клавишу Enter. В результате в ячейках (B 27:E 30) образуется матрица, обратная матрице коэффициентов СЛАУ.
Теперь необходимо скопировать матрицу, обратную матрице коэффициентов СЛАУ (ячейки (B 27:E 30)) в ячейки (C 32:F 35), а вектор свободных членов СЛАУ (ячейки (B 15:B 18)) в ячейки (H 32:H 35).
Алгоритм процедуры копирования множество, один из которых представлен в табл. 4.1.
Табл. № 4.1
Алгоритм копирования матрицы, обратной матрице коэффициентов СЛАУ
и вектора свободных членов СЛАУ
| № п/п |
Щелкнуть левой кнопкой манипулятора “мышь” по ячейке | Набрать в строке формул … и нажать Enter |
| Копировать матрицу |
||
| 1. | C32 | =B 27 |
| 2. | C33 | =B 28 |
| 3. | C34 | =B 29 |
| 4. | C35 | =B 30 |
| 5. | D 32 | =C 27 |
| 6. | D 33 | =C 28 |
| 7. | D 34 | =C 29 |
| 8. | D 35 | =C 30 |
| 9. | E 32 | =D 27 |
| 10. | E 33 | =D 28 |
| 11. | E 34 | =D 29 |
| 12. | E 35 | =D 30 |
| 13. | F 32 | =E 27 |
| 14. | F 33 | =E 28 |
| 15. | F 34 | =E 29 |
| 16. | F 35 | =E 30 |
| Копировать вектор свободных членов СЛАУ B (ячейки B 15:B 18)) в ячейки (H 32:H 35) | ||
| 1. | H 32 | =B 15 |
| 2. | H 33 | =B 16 |
| 3. | H 34 | =B 17 |
| 4. | H 35 | =B 18 |
Процедура копирования позволяет при изменении исходных данных СЛАУ (матрицы коэффициентов СЛАУ и вектора свободных членов СЛАУ) в ячейках (J
32:J
35) получать вектор решения СЛАУ, используя функцию умножения матриц =МУМНОЖ(C32:F35;H32:H35). Функцию умножения матриц возможно создать, используя мастер формул. Для этого необходимо выделить ячейки (J
32:J
35) и щелкнуть по пиктограмме MSExcel![]() , за тем в группе “Математические” выбрать функцию МУМНОЖ и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора “мышь”) элементы матрицы, обратной матрице коэффициентов СЛАУ (ячейки (C
32:F
35)), щелкнуть левой кнопкой манипулятора “мышь” в визуальном компоненте после метки с заголовком “Массив2”, выделить (при нажатой левой кнопки манипулятора “мышь”) элементы вектора свободных членов СЛАУ (ячейки (H
32:H
35)) и нажать кнопку “OK”. При закрытии окна “Аргументы функции” в выделенной области (ячейках (J
32:J
35)) для вектора решения СЛАУ сформируется только первый элемент вектора. Для формирования остальных элементов вектора решения СЛАУ следует нажать клавишу F
2, а за тем при одновременно нажатых клавишах Shift и Ctrl нажать клавишу Enter. В результате в ячейках (J
32:J
35) образуется вектор решения СЛАУ.
, за тем в группе “Математические” выбрать функцию МУМНОЖ и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора “мышь”) элементы матрицы, обратной матрице коэффициентов СЛАУ (ячейки (C
32:F
35)), щелкнуть левой кнопкой манипулятора “мышь” в визуальном компоненте после метки с заголовком “Массив2”, выделить (при нажатой левой кнопки манипулятора “мышь”) элементы вектора свободных членов СЛАУ (ячейки (H
32:H
35)) и нажать кнопку “OK”. При закрытии окна “Аргументы функции” в выделенной области (ячейках (J
32:J
35)) для вектора решения СЛАУ сформируется только первый элемент вектора. Для формирования остальных элементов вектора решения СЛАУ следует нажать клавишу F
2, а за тем при одновременно нажатых клавишах Shift и Ctrl нажать клавишу Enter. В результате в ячейках (J
32:J
35) образуется вектор решения СЛАУ.
Формулы на рис. 4.1 получены в редакторе формул MSEquation 3.0, поставляемом совестно с интегрированным пакетом прикладных программ MicrosoftOffice 2003.
Лист MSExcel, представленный на рис. 4.1 позволяет получить вектор решения для любой СЛАУ, состоящей из четырех уравнений. Описанная технология решения СЛАУ легко позволяет решить задачу любой размерности (для любого количества уравнений в СЛАУ).
4.2. Решение СЛАУ, используя метод "Поиск решения..."
(пункт главного меню "Сервис") MS Excel
Рассмотрим использование метода "Поиск решения..." на исходных данных представленных на рис. 4.1.
Для использования метода "Поиск решения..." необходимо свести задачу решения СЛАУ к задаче оптимизации. Введем целевую функцию вида
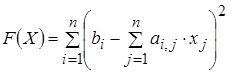 , (4.4)
, (4.4)
где bi – i -й элемент вектора свободных членов СЛАУ;
ai , j – i , j -й элемент матрицы коэффициентов СЛАУ;
xj – j -й элемент вектора решения СЛАУ;
n – количество уравнений в СЛАУ.
Ограничений на вектор решения X накладывать не будем.
Тогда математически задачу поиска вектора решения СЛАУ X можно записать
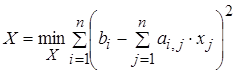 . (4.5)
. (4.5)
Подобная задача (4.5) легко решается использованием метода "Поиск решения..." MSExcel (см. рис. 4.2) следующим образом:
- обнуляем ячейки (B 29:B 32), в которых будем формировать вектор решения СЛАУ X ;
- для ячейки G
30 в строке формул запишем
=(B15-МУМНОЖ(B10:E10;B29:B32))^2+(B16-МУМНОЖ(B11:E11;B29:B32))^2+(B17-МУМНОЖ(B12:E12;B29:B32))^2+(B18-МУМНОЖ(B13:E13;B29:B32))^2 (см. 4.5)
правую часть целевой функции (4.4) для исходных данных нашей задачи;
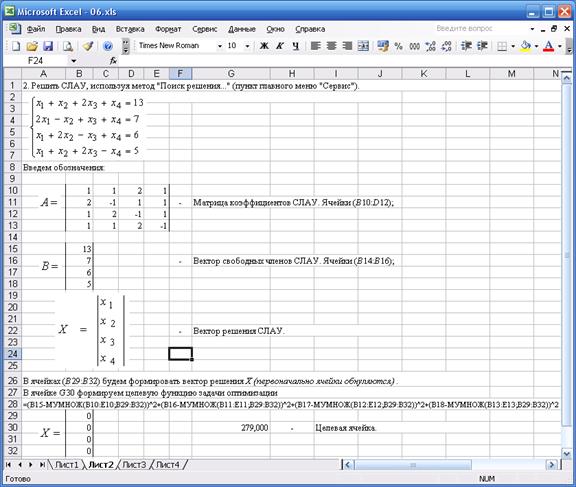
Рис. 4.2. Решение СЛАУ, используя метод "Поиск решения..."
(пункт главного меню "Сервис") MSExcel
- в пункте главного меню MSExcel "Се рвис" выбираем подпункт "Поиск решения..." (см. рис. 4.3).
При открытии окна "Поиск решения" напротив метки "Установить целевую ячейку:" будет отражен адрес активной ячейки (ячейки, в которой был установлен курсор при открытии окна). В ячейке $G $30 (G 30) должна быть записана формула вычисления правой части целевой функции (4.4). Также в окне "Поиск решения" ниже метки "Изменяя ячейки:" необходимо задать адрес вектора решения СЛАУ X ($ B $ 29:$ B $ 32) (B 29:B 32). Адреса целевой ячейки и вектора решения СЛАУ можно формировать в режиме конструктора. Для этого необходимо поместить курсор в ячейку формирования соответствующего адреса и на листе MSExcel выделить ячейку или массив ячеек;
- нажать кнопку "Выполнить". После чего появится окно "Результаты поиска решения" и в ячейках (B 29:B 32) сформируется вектор решения СЛАУ X .
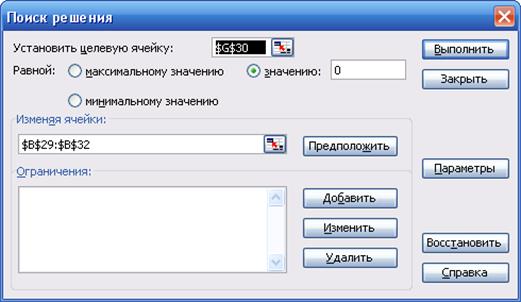
Рис. 4.3. Окно “Поиск решения…”
Лист MSExcel, представленный на рис. 4.2 позволяет получить вектор решения для любой СЛАУ, состоящей из четырех уравнений. Описанная технология решения СЛАУ легко позволяет решить задачу любой размерности (для любого количества уравнений в СЛАУ).
4.3. Решение СЛАУ методом Крамера (методом определителей)
СЛАУ из n уравнений задается матрицей коэффициентов СЛАУ A и вектором свободных членов СЛАУ B .
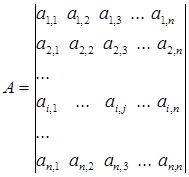 ;
; 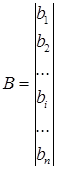 ,
,
где ai , j – i , j -й элемент матрицы коэффициентов СЛАУ;
bi – i -й элемент вектора свободных членов СЛАУ.
Суть метода Крамера в следующем: сначала вычисляется определитель матрицы коэффициентов СЛАУ
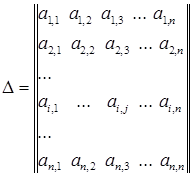 ,
,
за тем вычисляются еще n
определителей ![]()
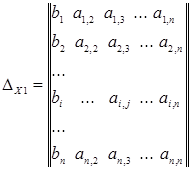 ,
,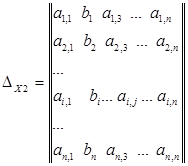 ,…,
,…,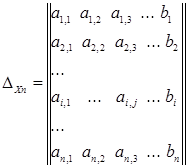 ,
,
т.е. определитель ![]() вычисляется для матрицы, полученной из матрицы коэффициентов СЛАУ путем замены j
-го столбца матрицы коэффициентов СЛАУ вектором свободных членов СЛАУ.
вычисляется для матрицы, полученной из матрицы коэффициентов СЛАУ путем замены j
-го столбца матрицы коэффициентов СЛАУ вектором свободных членов СЛАУ.
Тогда элементы вектора решения СЛАУ xj , j = 1, …, n определяются по формуле
![]() .
.
В MSExcel существует формула =МОПРЕД(левый_верхний_элемент_исходной_матрицы: правый_нижний_элемент_исходной_матрицы) для вычисления значений определителей квадратных матриц.
Решение СЛАУ методом Крамера (методом определителей) представлено на рис. 4.4.
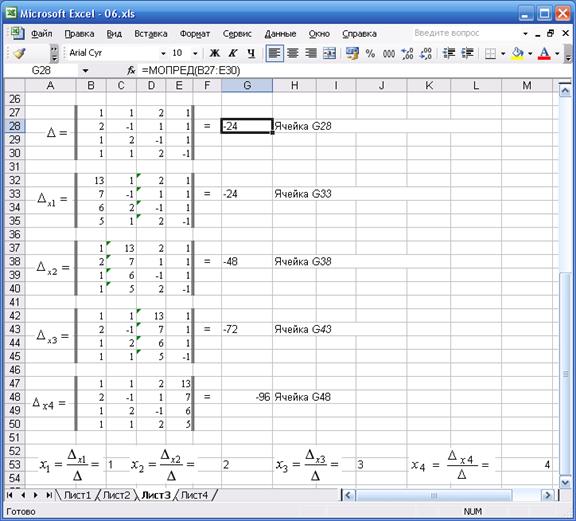
Рис. 4.4. Решение СЛАУ методом Крамера
Строки с 1 по 25 на рис. 4.4 не показаны, потому что они полностью совпадают с соответствующими строками рис. 4.1, 4.2.
Необходимо сформировать матрицы для вычисления определителей D, DX 1 , DX 2 , DX 3 в ячейках (B 27:E 30), (B 32:E 35), (B 37:E 40), (B 42:E 45), (B 47:E 50), соответственно. Алгоритм формирования матриц для вычисления определителей представлен в табл. 4.2.
Табл. № 4.2
Алгоритм формирования матриц для вычисления определителей
| № п/п |
Щелкнуть левой кнопкой манипулятора “мышь” по ячейке | Набрать в строке формул … и нажать Enter |
| Формирование матрицы для вычисления определителя D | ||
| 1. | B 27 | =B 10 |
| 2. | B 28 | =B 11 |
| 3. | B 29 | =B 12 |
| 4. | B 30 | =B 13 |
| 5. | С 27 | =C 10 |
| 6. | С 28 | =C 11 |
| 7. | С 29 | =C 12 |
| 8. | С 30 | =C 13 |
| 9. | D 27 | =D 10 |
| 10. | D 28 | =D 11 |
| 11. | D 29 | =D 12 |
| 12. | D 30 | =D 13 |
| 13. | E 27 | =E 10 |
| 14. | E 28 | =E 11 |
| 15. | E 29 | =E 12 |
| 16. | E 30 | =E 13 |
| Формирование матрицы для вычисления определителя DX 1 | ||
| 1. | B 32 | =B 15 |
| 2. | B 33 | =B 16 |
| 3. | B 34 | =B 17 |
| 4. | B 35 | =B 18 |
| 5. | C 32 | =C 10 |
| 6. | C 33 | =C 11 |
| 7. | C 34 | =C 12 |
| 8. | C 35 | =C 13 |
| 9. | D 32 | =D 10 |
| 10. | D 33 | =D 11 |
| 11. | D 34 | =D 12 |
| 12. | D 35 | =D 13 |
| 13. | E 32 | =E 10 |
| 14. | E 33 | =E 11 |
| 15. | E 34 | =E 12 |
| 16. | E 35 | =E 13 |
| Формирование матрицы для вычисления определителя DX 2 | ||
| 1. | B 37 | =B 10 |
| 2. | B 38 | =B 11 |
| 3. | B 39 | =B 12 |
| 4. | B 40 | =B 13 |
| 5. | C 37 | =B 15 |
| 6. | C 38 | =B 16 |
| 7. | C 39 | =B 17 |
| 8. | C 40 | =B 18 |
| 9. | D 37 | =D 10 |
| 10. | D 38 | =D 11 |
| 11. | D 39 | =D 12 |
| 12. | D 40 | =D 13 |
| 13. | E 37 | =E 10 |
| 14. | E 38 | =E 11 |
| 15. | E 39 | =E 12 |
| 16. | E 40 | =E 13 |
| Формирование матрицы для вычисления определителя DX3 | ||
| 1. | B 42 | =B 10 |
| 2. | B 43 | =B 11 |
| 3. | B 44 | =B 12 |
| 4. | B 45 | =B 13 |
| 5. | C 42 | =C 10 |
| 6. | C 43 | =C 11 |
| 7. | C 44 | =C 12 |
| 8. | C 45 | =C 13 |
| 9. | D 42 | =B 15 |
| 10. | D 43 | =B 16 |
| 11. | D 44 | =B 17 |
| 12. | D 45 | =B 18 |
| 13. | E 42 | =E 10 |
| 14. | E 43 | =E 11 |
| 15. | E 44 | =E 12 |
| 16. | E 45 | =E 13 |
| Формирование матрицы для вычисления определителя DX 4 | ||
| 1. | B 47 | =B 10 |
| 2. | B 48 | =B 11 |
| 3. | B 49 | =B 12 |
| 4. | B 50 | =B 13 |
| 5. | C 47 | =C 10 |
| 6. | C 48 | =C 11 |
| 7. | C 49 | =C 12 |
| 8. | C 50 | =C 13 |
| 9. | D 47 | =D 10 |
| 10. | D 48 | =D 11 |
| 11. | D 49 | =D 12 |
| 12. | D 50 | =D 13 |
| 13. | E 47 | =B 15 |
| 14. | E 48 | =B 16 |
| 15. | E 49 | =B 17 |
| 16. | E 50 | =B 18 |
Алгоритм вычисления определителей представлен в табл. 4.3.
Табл. № 4.3
Алгоритм вычисления определителей
| № п/п |
Щелкнуть левой кнопкой манипулятора “мышь” по ячейке | Набрать в строке формул … и нажать Enter |
| 1. | G 28 (определитель D) | =МОПРЕД(B 27:E 30) |
| 2. | G 33 (определитель DX 1 ) | =МОПРЕД(B 32:E 35) |
| 3. | G 38 (определитель DX 2 ) | =МОПРЕД(B 37:E 40) |
| 4. | G 43 (определитель DX 3 ) | =МОПРЕД(B 42:E 45) |
| 5. | G 48 (определитель DX 4 ) | =МОПРЕД(B 47:E 50) |
Возможно вычисление определителей в режиме конструктора. Для этого необходимо выделить ячейку, в которой вычисляется определитель, например, G
28 и щелкнуть по пиктограмме MSExcel![]() , за тем в группе “Математические” выбрать функцию МОПРЕД и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора мышь) элементы исходной матрицы, например, ячейки (B
27:E
30) и нажать кнопку “OK”.
, за тем в группе “Математические” выбрать функцию МОПРЕД и нажать кнопку “OK”. После появления окна “Аргументы функции” выделить (при нажатой левой кнопки манипулятора мышь) элементы исходной матрицы, например, ячейки (B
27:E
30) и нажать кнопку “OK”.
Вектор решения СЛАУ X определяется в строке 53. Алгоритм формирования вектора решения представлен в табл. 4.4.
Табл. № 4.4
Алгоритм формирования вектора решения СЛАУ X
| № п/п |
Щелкнуть левой кнопкой манипулятора “мышь” по ячейке | Набрать в строке формул … и нажать Enter |
| 1. | C 53 | =G 33/G 28 |
| 2. | G 53 | =G 38/G 28 |
| 3. | J 53 | =G 43/G 28 |
| 4. | M 53 | =G 48/G 28 |
В результате в ячейках (C 53, G 53, J 53, M 53) сформируется вектор решения СЛАУ X (см. рис. 4.4).
Лист MSExcel, представленный на рис. 4.4 позволяет получить вектор решения для любой СЛАУ, состоящей из четырех уравнений. Описанная технология решения СЛАУ легко позволяет решить задачу любой размерности (для любого количества уравнений в СЛАУ).
ЗАКЛЮЧЕНИЕ
Основная цель компьютерного практикума по дисциплине “Информатика”, заключающаяся в получении и закреплении навыков подготовки пояснительных записок (ПЗ)
· к контрольным работам;
· рефератам;
· курсовым работам (КР) и проектам (КП);
· выпускным квалификационным работам (ВКР).
достигнута.
Выполнены четыре вида заданий:
· разработки схемы алгоритма решения конкретной задачи;
· построения графика с элементами вычисления функции;
· построения диаграммы, отражающей изменение состояния процесса (объекта);
· решения системы линейных алгебраических уравнений.
ПЗ отчета о практикуме содержит все необходимые объекты: титульный лист, “ОГЛАВЛЕНИЕ”, формулы, рисунки, таблицы, список литературы и ссылки на источники.
СПИСОК ЛИТЕРАТУРЫ
1.Ильин А.А., Евсюков В.В., Ильин Р.А. Информатика (с грифом УМО по образованию в области прикладной информатики): Учебное пособие. - М.: Серебряная нить. 2005. - 376 с.
2.Ильин А.А. и др. Информационные технологии управления: Учебное пособие (с грифом УМО по образованию в области прикладной информатики) / под ред. Ю.В. Обрубова. - М.: Изд-во "Ваш Домъ", 2006. - 192 с.
3.Ильин А.А. Методические указания подготовки компьютерного практикума и оформлению отчета по дисциплине “Информатика”. – Тула: НОУ ВПО Тульский институт управления и бизнеса, 2009. – 30 с.
[1] Отсутствие на занятии;
[2] Присутствие на занятии.