| Скачать .docx |
Реферат: Управление сложными системами
Лекция №1. 11.02.2003
Раздел 1. Основные понятия теории сложности
1.1. Сложность
Сложность — свойство современных систем управления.
Различают следующие понятия сложности:
1) Математическое
2) Информационное
3) Структурное
4) Обобщенное
5) Алгоритмическое
6) и др.
Математическое понятие относится к теории конечных автоматов. 50-е гг XX века. Основная характеристика сложности системы — число элементарных блоков, образующих систему.
Информационное понятие введено Колмогоровым и относится к теории информации. Сложность здесь связана со случайностью. Основная характеристика сложности системы — спектр частот. Вроде бы такого понятия достаточно для оценок свойств системы, но все же есть недостаток: не учитываются комбинации подсистем в системе.
В структурном понятии учитываются взаимосвязи между подсистемами в системе. Систему формируют таким образом, чтобы она обладала определенными статическими и динамическими характеристиками. Основная характеристика сложности системы — статические (установившееся состояние системы) и динамические (переходные режимы системы) свойства системы.
При реализации системы стремятся использовать наиболее простые технические средства. Таким образом, косвенно учитываются требования надежности и стоимости. Учет надежности и экономичности на этапе проектирования делает эту задачу более корректной. Кроме того, любая задача должна быть математически корректной (математическая корректность — сходимость алгоритмов управления). Неустойчивость алгоритмов обусловлена 1) неточностью исходных данных, 2) неточностью их реализации в компьютере на этапе проектирования или в ВК (вычислительном Комплексе) при работе с системой.
В обобщенном понятии основная характеристика сложности системы — шкала сложности. Основные признаки построения шкалы сложности:
— порядок дифференциального оператора
— спектр частот
— основные характеристики ВК
— надёжность
— стоимость
— алгоритмическая сложность
— и др.
1.2 Иерархия
Когда проблемой является определение свойств системы по характеристикам отдельных подсистем, используется иерархический подход, позволяющий решить эту проблему.
Основные признаки иерархии:
1. Сложные иерархические структуры являются многоуровневыми, на определенных уровнях которых принимаются решения;
2. Общая (глобальная) и местная (локальная) цели функционирования должны координироваться;
3. Между уровнями системы происходит обмен информацией, при этом приоритетом обладает информация, поступающая с верхнего уровня. Для нижнего уровня она является командной и подлежит выполнению, если это возможно;
4. Процесс обмена информацией снизу вверх в структуре замедляется.
1.3 Типовая структура сложной системы
Обобщенную структуру сложной системы можно представить в виде треугольной структуры (смотри рисунок №1).
Уровни: О, 1, 2, 3, 4.
О — объект управления, который тоже является сложным, например, состоящим из восьми подсистем О.1 – О.8.
На рисунке №1:
Х1 – Х8 — регулируемые переменные.
r1 – r8 — регулирующее воздействие.
И — информация. У — уставка, управления.
1 — уровень локального регулирования.
Используются аналоговые или цифровые (например, микропроцессорные системы из следующего семестра) Системы Автоматического Регулирования (САР), которые осуществляют непосредственное регулирование объектами О.1 – О.8.
2 — уровень локальной оптимизации.


Рисунок №2
Здесь оптимизаторы Системы Автоматического Управления (в них уставка вырабатывается ВК) или Автоматизированные Системы Управления (в них уставка определяется человеком совместно с ВК, который нужен для усиления интеллекта человека) осуществляют оптимальное управление локальными регуляторами первого уровня в соответствии с частными критериями.
3 — уровень координации.
Здесь реализуется второй признак иерархии.
4 — уровень оперативного управления
ЛПР — лицо, принимающее решение.
Общая цель работы системы трансформируется в конкретные уставки нижним уровням, распределяются ресурсы, принимаются решения в нештатных ситуациях и др.
Основой для решения являются мощные ВК и «быстрые» математические модели.
1.4 Эквивалентная структура сложной системы (Даймонд–структура)
Структуру треугольного типа можно представить в виде структуры ромбовидного типа (смотри рисунок №2).
В данной структуре разделены информационная и управляющая (уровни принятия решения) функции.
1. Такое преобразование обеспечивает наглядность, так как разделены информационная и управляющая функции.
2. Возможность выполнять вертикальный разрез системы и проводить анализ и синтез динамических структур САУ или АСУ.
3. Выполнять горизонтальное сечение и решать задачи статического расчета на заданном уровне (информационном или управляющем).
4. Формализовать процессы информационные и управляющие, что облегчает работу математической модели системы.
На рисунке №2:
~~
1.1 – 1.8 — датчики (измерительные устройства локальных регуляторов).
~ ~ ~ ~ ~
2.1 – 2.4; 3.1 – 3.2; 4.1 — информационные системы соответствующих уровней.
/\ /\
1.1 – 1.8 — собственно локальные регуляторы САР без датчиков.
/\/\/\/\/\
2.1 – 2.4; 3.1 – 3.2; 4.1 — соответствующие подсистемы без информационных подсистем.
АСУ — характерный пример сложной системы (СС). В частности АСУТП.
Раздел 2. АСУТП.
АСУТП — человеко-машинная система, обеспечивающая сбор и обработку информации для оптимизации управления технологическим (техническим) процессом (объектом) в соответствии с принятым критерием.
Лекция №2. 12.02.2003
2.1Фнукции АСУТП
1) Информационные (обеспечивают сбор, обработку и представление информации персоналу);
2) Управляющие (на основе полученной информации выработка оптимальных управляющих воздействий и их реализация);
3) Вспомогательные (внутрисистемные задачи по функционированию технических и программных средств).
2.2 Структура АСУТП
Структуру системы образуют:
1. Оперативный персонал.
2. Техническое обеспечение.
3. Информационное обеспечение.
4. Организационное обеспечение.
5. Математическое обеспечение.
6. Программное обеспечение.
7. Лингвистическое обеспечение.
8. и др.
1) Оперативный персонал — группа операторов (диспетчеров), которые осуществляют контроль и управление объектом (или процессом), а также эксплуатационный персонал, обеспечивающий работу программных и технических средств.
2) Техническое обеспечение — комплекс технических средств АСУТП, в том числе и ВК.
3) Информационное обеспечение — совокупность реализованных решений по объемам, размещению и формам организации информации, циркулирующей в системе. Оно определяет формы и способы представления информации по состоянию системы (в виде баз данных, файлов ВК, других документов и сигналов для представления персоналу).
4) Организационное обеспечение — совокупность документов, регламентирующих деятельность персонала в АСУТП.
5) Математическое обеспечение — совокупность математических методов, моделей и алгоритмов, используемых при проектировании и работе системы.
На этапе анализа информации и принятия решения необходимо формулировать задачи управления математически. Для этого необходимы:
— Математическая Модель (ММ);
— Критерий управления;
— Учет ограничений.
ММ — совокупность математических отношений, описывающих поведение объекта и условия его работы.
Для составления ММ необходимо знать физическую природу явления, структуру и особенности объекта. Любая ММ неадекватна и трудоёмка.
Неадекватность (приближенность):
— неточность основных законов;
— определяется техническим средством — ВК.
При “закладке” ММ в компьютер приходится прибегать к упрощениям. Разработка ММ может занимать до 60 – 80 % общего времени проектирования системы.
Алгоритм — инструкция решения данной задачи, выраженная на языке математических формул и логических условий.
Алгоритм управления — инструкция для получения целесообразных управляющих воздействий, в которой говорится о том, как надо обрабатывать информацию об объекте.
6) Программное обеспечение делится на общее (сопровождают данные ВК) и специальное (разрабатывается для конкретной системы и для реализации основных функций этой системы).
7) Лингвистическое обеспечение — совокупность языковых средств формализации естественного языка обеспечения персонала ВК.
Основное требование: язык должен быть лаконичен, быстро и однозначно воспринимаем.
2.3 Типовая функциональная схема и примеры АСУТП
Множество АСУТП можно классифицировать по различным признакам, в том числе по роли человека–оператора и ВК. Распределение функций между ними осуществляется на этапе предварительного проектирования. Более совершенна та система, где максимум функций выполняет ВК.
1 — Человек оператор
2 — ВК
3 — Объект управления
4 — Система отображения информации
5 — Пульт или пост управления
6 — Устройство логического управления
7 — Локальные регуляторы
8 — Исполнительные устройства
9 — Измерительные устройства
10 — АСУТП более высокого уровня
11 — Система сигнализации
12 — Система аварийной защиты
13, 14 — Функциональные связи

2.3.1 АСУТП с информационным типом функционирования
В данном случае нет связей 13 и 14.
ВК, получая информацию, обрабатывает её и с помощью СОИ (Систем Отображения Информации) представляет человеку–оператору. Оператор анализирует информацию и принимает решение, воздействует на объект при помощи технических средств №№ 5, 6, 7, 8.
ВК выполняет следующие функции:
1. Сбор информации для уточнения ММ.
2. Рассчитывание технических и технико-экономических показателей.
3. Контроль работы системы.
4. Связь с АСУТП более высокого уровня.
Следовательно, система существенно зависит от человека–оператора.
2.3.2 АСУТП с функционированием в режиме “советчика”
В данном случае нет связей 13 и 14.
ВК рассчитывает возможные варианты решения (уставки), которые предлагаются оператору. Оператор анализирует их и выбирает более рациональную уставку.
В такой системе влияние оказывает субъективный фактор человека–оператора.
2.3.3 АСУТП с супервизорным управлением
В данном случае используется функциональная связь 13, а 14 отсутствует.
ВК рассчитывает уставки локальным регулятором (7). Человек–оператор, находясь вне основного контура, контролирует работу системы и вмешивается в процесс по мере необходимости.
2.3.4 АСУТП с непосредственным цифровым управлением
В данном случае используется функциональная связь 14, а 13 отсутствует.
ВК рассчитывает не уставки, а необходимые управляющие воздействия на объект, которые реализуются исполнительными устройствами (8). При этом локальные регуляторы, выносящиеся за пределы контура, являются дополнительными.
2.35 Комбинированные АСУТП
Пример — смотри ДЗ.
Раздел 3. Локальные оптимизаторы и регуляторы
3.1 Обобщенная структура локального оптимизатора САУ. Проблемы управления

1 — управляемая система; 2 — управляющая система.
Пусть известны:
1. Цель управления (Е) в виде показателя — функционала. ![]() (1)
(1)
2. Математическая модель в виде системы дифференциальных уравнений ![]() (2)
(2)
3. Ограничения:  (3)
(3)
Изменение векторов состояния ![]() , управления
, управления ![]() ограничено замкнутыми областями А и В, которые в свою очередь являются составляющими соответственно пространств состояний Х и управления Y.
ограничено замкнутыми областями А и В, которые в свою очередь являются составляющими соответственно пространств состояний Х и управления Y.
Тогда: Проблема управления состоит
в определении такого вектора управления ![]() , который обеспечивал бы экстремум функционала (1) при известных ММ (2) и ограничениях (3).
, который обеспечивал бы экстремум функционала (1) при известных ММ (2) и ограничениях (3).
![]() — многомерные векторные функции соответствия
— многомерные векторные функции соответствия
![]() — состояния;
— состояния; ![]() — управления;
— управления; ![]() — наблюдения;
— наблюдения; ![]() — возмущения.
— возмущения.
То есть  , — переменные состояния.
, — переменные состояния.
![]() — наблюдаемые переменные, то есть переменные состояния, информация об изменении которых поступает в управляющую систему.
— наблюдаемые переменные, то есть переменные состояния, информация об изменении которых поступает в управляющую систему.
Лекция №3. 18.02.2003
 — управляющие воздействия (уставки).
— управляющие воздействия (уставки).
![]() — возмущающие воздействия.
— возмущающие воздействия.
3.2 Обобщенная структура локального регулятора САР. Проблемы управления.

1 — объект регулирования;
2 — регулятор (контроллер);
3 — устройство сравнения.
![]() — вектор регулирования;
— вектор регулирования;
![]() — регулирующее воздействие.
— регулирующее воздействие.
![]() — вектор ошибки.
— вектор ошибки.
В данном случае:
1. ![]() — известен.
— известен.
2. ![]()
3. Показатель точности ![]()
Тогда: Проблема регулирования состоит
в определении такого вектора регулирования ![]() (алгоритма), который обеспечивал бы минимум n частных показателей эффективности
(алгоритма), который обеспечивал бы минимум n частных показателей эффективности ![]() , каждый из которых зависит от одной из составляющих вектора ошибки, при изменяющихся связях (2) и ограничениях (3).
, каждый из которых зависит от одной из составляющих вектора ошибки, при изменяющихся связях (2) и ограничениях (3).
Задача регулирования — это частный случай проблемы управления, а локальный регулятор является объектом локального оптимизатора (смотри Рисунки №№1, 2).
3.2.1 Типовая функциональная схема локального регулятора. Состав элементов

![]() — источники энергии.
— источники энергии.
1 — преобразующее устройство;
2 — последовательное корректирующее устройство (аналоговое или цифровое (микропроцессор)) (придаёт системе требуемые свойства);
3 — усилительное устройство;
4 — исполнительное устройство;
5 — параллельное корректирующее устройство (включается встречно-параллельно и охватывает звенья подсистемы с наиболее неблагоприятными свойствами);
6 — объект регулирования;
7 — элемент (устройство) главной обратной связи;
8 — местная обратная связь;
9 — главная обратная связь.
Локальные регуляторы содержат в своей структуре измерительные, усилительные, исполнительные и корректирующие устройства. Пример системы: смотри ДЗ.
Следовательно, САР — замкнутая динамическая система использования получающихся сигналов для управления источниками энергии, стремящаяся сохранить в допустимых пределах ошибки между требуемыми и действительными значениями регулируемых переменных путем их сравнения.
3.2.2 Основные типы локальных регуляторов
Множество локальных регуляторов можно упорядочить по различным признакам:
Во-первых , в зависимости от характера информации, используемой в регуляторе:
1.) С регулированием по разомкнутому циклу (по возмущениям).

Проблема состояла в определении регулирующего воздействия.
Здесь регулятор настраивается в зависимости от основного возмущения ![]() .
.
“+”: высокое быстродействие, так как регулятор настраивается сразу по возмущению, а не так, как в случае регулирования по замкнутому циклу.
“–”: трудность программирования регулятора на возможные возмущения, следовательно, невысокая точность.
2.) С регулированием по замкнутому циклу (по отклонениям).

“+”: в независимости от причин появления ошибки ![]() , система работает по принципу её (ошибки) компенсации.
, система работает по принципу её (ошибки) компенсации.
“–”: быстродействие ниже, чем в случае с регулированием по разомкнутому циклу.
3.) С регулированием по комбинированию.
Объединение случаев регулирования по разомкнутому циклу и по замкнутому циклу.
Во-вторых
, в зависимости от уставки ![]() :
:
1.) Системы стабилизации ![]() .
.
2.) Программные системы ![]() , причём
, причём ![]() — известно.
— известно.
3.) Следящие системы ![]() , причём
, причём ![]() — заранее неизвестная функция.
— заранее неизвестная функция.
В-третьих
, в зависимости от размерности n вектора состояния ![]() :
:
1.) Одномерные n = 1.
2.) Двумерные n = 2.
3.) Многомерные n = 3.
В-четвёртых , в зависимости от количества контуров в системе:
1.) Одноконтурные (используется только главная обратная связь, нет местных связей).
2.) Двухконтурные (используются одна главная и одна местная обратные связи).
3.) Многоконтурные (используются одна главная и много местных обратных связей).
В-пятых , в зависимости от установившегося значения ошибки:
1.) Статические ![]() .
.
2.) Астатические ![]() .
.
Систему называют астатической по управляющему (или возмущающему) воздействию, если при подаче на вход постоянного управляющего (или возмущающего) воздействия ошибка в установившемся состоянии не зависит от величины этого воздействия и равна нулю.
Сравнить рисунки 24 и 26 методических указаний.
В-шестых , в зависимости от характеров сигналов, циркулирующих в системе:
1.) Непрерывные.
2.) Импульсные.
3.) Релейные.
4.) Релейно-импульсные (кодово-импульсные).
5.) На переменном токе (с гармонической модуляцией).
1.) В непрерывных системах сигналы могут быть описаны непрерывными во времени функциями.
3.2.2.1 Импульсные системы
Эти системы содержат импульсные устройства (2), осуществляющие квантование сигналов по времени (АИМ).
Типовая структура импульсных систем:

1 — непрерывная часть системы.
Импульсное устройство (ключ), замыкаясь в дискретные равноотстоящие моменты времени (t = i∙T, i = 0, 1, 2, …, где i — период повторения, а T — период дискретности), преобразует непрерывный входной сигнал ![]() в дискретный
в дискретный ![]() .
.
Реальный ключ (2) удобно условно представить в следующем виде:

3 — идеальный ключ; 4 — формирователь.

Лекция №4. 19.02.2003
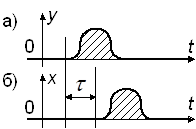
Идеальный ключ (3) преобразует непрерывный сигнал ![]() (рисунок а)) в последовательность идеальных импульсов типа δ-функций (рисунок б)), далее эта последовательность поступает на формирователь (4).
(рисунок а)) в последовательность идеальных импульсов типа δ-функций (рисунок б)), далее эта последовательность поступает на формирователь (4).
Формирователь (4) преобразует эту последовательность в реальные импульсы определённой формы, длительности (γT, 0<γ≤1) и амплитуды (рисунок в)).
При запоминании на интервале дискретности T при γ = 1 формирователь (4) называют Экстраполятором Нулевого Порядка (Э0П).
Математическая модель Э0П непрерывна и может быть отнесена к непрерывной части системы. В результате типовая структура импульсной системы примет вид:

Рисунок № !
5 — приведенная непрерывная часть;
6 — импульсный фильтр
3.2.2.2 Релейные системы
Релейные системы содержат в своей структуре устройства (реле), осуществляющие квантование сигнала по уровню. В результате, на выходе реле сигнал будет непрерывным, но ступенчатым
3.2.2.3 Релейно-импульсные системы
В них происходит квантование сигналов по времени и по уровню.
К этому типу относятся цифровые системы управления, в частности АСУТП с используемым ВК.
При большом количестве разрядов АЦП и ЦАП квантованием можно пренебречь, и отнести такие системы к импульсным.
3.2.2.4 Системы на переменном токе
В них содержится модулятор, осуществляющий один из видов гармонической модуляции (всего их три: АМ, ЧМ, ФМ).
В-седьмых , в зависимости от вида используемой энергии:
1.) Механические.
2.) Электрические.
3.) Пневматические.
4.) На горячем газе.
5.) Гидравлические.
6.) Комбинированные.
В-восьмых , в зависимости от степени идеализации математической модели:
Смотри Раздел №4.
В-девятых , и т.д.
3.3 Требования, предъявляемые к системам
Помимо подхода, рассмотренного выше, при проектировании систем управления можно использовать ряд требований, которые определяют допустимые условия работы, а именно:
1.) к устойчивости;
2.) к качеству регулирования;
3.) к динамической точности;
4.) к управляемости;
5.) к наблюдаемости;
6.) к условиям эксплуатации;
7.) к стоимости;
8.) к др.
3.3.1 Устойчивость
В системах управления часть энергии с выхода системы подаётся на вход (обратная связь), энергия не может изменяться мгновенно, кроме того существуют запаздывания, а системы по своей природе являются колебательными. Поэтому, при определённых условиях система вместо подавления колебаний может стать их генератором, то есть неустойчивой.
3.3.2 Качество регулирования
Устойчивость определяет свободное движение системы, когда внешнее воздействие отсутствует. Важно определить поведение системы при наличии таковых. Поэтому анализируют качество регулирования при наиболее неблагоприятных или типовых воздействиях:
3.3.2.1 Единичное ступенчатое воздействие
1.) Несмещенное ![]() , т.е.
, т.е. ![]() .
.

2.) Смещенное ![]() , т.е.
, т.е. ![]() .
.

Ступенчатое воздействие может быть и неединичным: ![]() ,
, ![]()
Переходная функция h ( t ) — реакция системы на единичное ступенчатое воздействие.
3.3.2.2 δ-функция. Импульсное воздействие
1.) Несмёщенная δ-функция ![]() .
.

Свойства несмещённой δ-функции:
1. ![]() . 2.
. 2. ![]() .
.
3. Если ![]() непрерывная ограниченная функция, то
непрерывная ограниченная функция, то ![]() .
.
4. ![]() .
.
2.) Смещённая δ-функция ![]() .
.
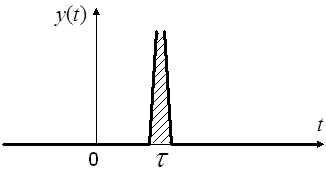
Свойства смешённой δ-функции:
1. ![]() . 2.
. 2. ![]() .
.
3. Если ![]() непрерывная ограниченная функция, то
непрерывная ограниченная функция, то ![]() .
.
4. Пусть ![]() непрерывное воздействие произвольного вида, например:
непрерывное воздействие произвольного вида, например:

Следовательно, ![]() .
.
Импульсная переходная функция k ( t ) или функция веса (весомости) — реакция системы на δ-функцию.
3.3.2.3 Гармоническое воздействие
а) ![]() .
.
б) ![]() .
.
Такое воздействие позволяет:
1) При анализе вынужденного установившегося движения определить частотные характеристики системы.
2) Определив реакцию системы на гармоническое воздействие б) и разложив периодическое воздействие ![]() в ряд Фурье, с учётом принципа суперпозиций можно определить реакцию системы на это воздействие (
в ряд Фурье, с учётом принципа суперпозиций можно определить реакцию системы на это воздействие (![]() ).
).
3.3.2.4 Типовое воздействие “постоянная скорость”
![]() ,
, ![]() .
.
3.3.2.5 Типовое воздействие “постоянное ускорение”
![]() ,
, ![]() .
.
3.3.3 Динамическая точность
Реальные системы работают в условиях, когда воздействия могут быть случайными; при этом отсутствует установившееся состояние в системе, и важно оценить поведение системы в переходном режиме.
Тогда в качестве основной характеристики рассматривают динамическую точность. Мерой динамической точности часто служит среднее значение квадрата ошибки ![]() (или дисперсия ошибки).
(или дисперсия ошибки).
3.3.4 Управляемость систем
Понятие управляемости означает, можно ли, вообще, управлять системой. Иногда это можно установить по структуре системы:
Пример № 1.

Система неуправляема, так как управление ![]() не управляет второй подсистемой.
не управляет второй подсистемой.
3.3.5 Наблюдаемость
С качественной точки зрения под наблюдаемостью системы понимают способность состояния системы создавать выходной сигнал.
Пример № 2.

Система не наблюдаема, так как измеряется ![]() , а
, а ![]() не измеряется.
не измеряется.
Пример № 3.

1 подсистема — управляема и наблюдаема.
2 подсистема — управляема и не наблюдаема.
3 подсистема — не управляема и наблюдаема.
4 подсистема — не управляема и не наблюдаема.
Лекция №5. 25.02.2003
Раздел 4. Математические модели систем управления
4.1. Основные виды математических моделей
Математические модели могут быть:
1.) Линейными;
2.) Нелинейными
В свою очередь каждая из них может быть:
1.) Непрерывной (система дифференциальных или интегро-дифференциальных уравнений);
2.) Дискретной (система разностных уравнений);
3.) Дискретно-непрерывной (сочетание непрерывной и дискретной систем).
В свою очередь каждая из них может быть:
1.) Стационарной;
2.) Нестационарной.
Математическая модель нестационарна , если хотя бы один из параметров системы изменяется с течением времени.
В свою очередь каждая из них может быть:
1.) С сосредоточенными параметрами;
2.) С сосредоточенными и распределёнными параметрами.
1.) Физические параметры системы (например, масса, скорость, потенциал и др.) обычно сосредоточены в точке (так можно считать), коэффициенты дифференциальных уравнений зависят от этих параметров. В результате, математическая модель будет, например, системой дифференциальных уравнений в полных производных (![]() ).
).
2.) Если система содержит одну из подсистем (например, канал связи, трубопровод), параметры которой распределены в пространстве, то математическая модель такой системы будет содержать, например, систему дифференциальных уравнений в частных производных (![]() ).
).
В свою очередь каждая из них может быть:
1.) Детерминированной;
2.) Стохастической или со случайными параметрами (если хотя бы один из параметров или воздействий является случайной функцией или величиной).
и др.
4.1.1 Математические модели в области вещественной переменной (временной области)
4.1.1.1 Дискретные математические модели
4.1.1.1.1 Решетчатые функции
Решетчатая функция (РФ) — функция, существующая в дискретны равноотстоящие друг от друга значения независимой переменной и равная нулю между этими значениями аргумента.
Пример такой функции:
смотри рисунок б) лекции №3.

![]() — РФ,
— РФ, ![]()

![]()
Функции f
(
t
)
соответствует функция ![]() ,
, ![]() (
(![]() )
)
Одной и той же РФ соответствует множество огибающих непрерывных функций (смотри рисунок выше):
![]()
![]() — огибающие функции.
— огибающие функции.
Если ввести безразмерное время ![]() , то
, то ![]() будет соответствовать РФ
будет соответствовать РФ ![]() .
. ![]()
Решетчатую функцию характеризуют её разности и суммы
Разность может быть прямой (![]() ) и обратной (
) и обратной (![]() ).
).

![]()
![]()
![]()
![]()
![]() .
.
Аналогом интеграла непрерывной функции для РФ являются её суммы:
1) Полная  ;
;
2) Неполная .
.
4.1.1.1.2 Разностные уравнения.
Связь между решетчатой функцией и её разностями устанавливают разностные уравнения, например:
Линейное разностное уравнение
![]()
![]() (I΄)
(I΄)
Или через дискреты РФ:
![]()
![]()
![]() (I)
(I)
Уравнение (I) — это алгоритм решения разностного уравнения при известных начальных условиях, воздействиях y и f и дискретах искомой РФ x в предшествующие моменты времени.
Коэффициенты уравнения (I) однозначно вычисляются из уравнения (I’).
4.1.1.2 Непрерывные математические модели
Математическая модель системы может быть получена на основе математических моделей подсистем, образующих данную систему.
4.1.1.2.1 Математическая модель системы
Рассмотрим в качестве примера непрерывную стационарную одномерную детерминированную систему с сосредоточенными параметрами

Всего три подсистемы: объект ![]() , регулятор
, регулятор ![]() и элемент сравнения
и элемент сравнения ![]() .
.
Объект — динамическая система, дифференциальные уравнения которой могут быть записаны следующим образом:
![]()
Х — любая линейная или нелинейная функция.
Составим уравнение регулятора:
Регулятор — также динамическая система, при этом с учётом направленности действия уравнение регулятора не будет содержать х :
![]()
Примечание. Направленность действия означает то, что объект не оказывает обратного влияния на регулятор, а только через элемент сравнения и главную обратную связь
Составим уравнение элемента сравнения:
![]()
Система уравнений ![]() ,
, ![]() ,
, ![]() — это математическая модель рассматриваемой системы.
— это математическая модель рассматриваемой системы.
В общем случае это система нелинейных дифференциальных уравнений.
4.1.1.2.2 Линеаризация математической модели
Если нелинейности системы несущественны, то ими пренебрегают, и считают модель линейной с какой-то степенью приближения.
Линейные модели используют обычно на этапе предварительного проектирования, они удобны для исследования.
Применяя соответствующий метод линеаризации, можно перейти от линейной модели к линеаризованной.
Рассмотрим один из этих методов:
он опирается на гипотезу малости отклонений “Δ”-вариаций переменных х(
t
),
y
(
t
),
r
(
t
),
f
(
t
),
![]() от их значений, от их заданных или фиксированных значений “0” х0
(
t
),
y
0
(
t
),
r
0
(
t
),
f
0
(
t
),
от их значений, от их заданных или фиксированных значений “0” х0
(
t
),
y
0
(
t
),
r
0
(
t
),
f
0
(
t
),
![]() , например, в установившемся состоянии.
, например, в установившемся состоянии.
Рассмотрим уравнение объекта ![]() :
:
Полагая ![]() и
и ![]() , решения уравнения
, решения уравнения ![]() можно найти в виде
можно найти в виде ![]() , а уравнения
, а уравнения ![]() в виде
в виде ![]() , тогда:
, тогда:
![]()
![]()
Лекция №6. 26.02.2003
Если X непрерывная и однозначная функция, то её можно разложить в ряд Тейлора в окрестности некоторых точек х0 , r 0 , f 0 :
![]()


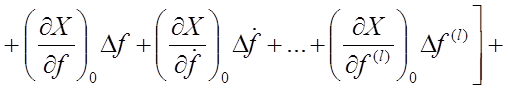
![]() .
.
Пренебрегая членами ряда порядка выше первого (из-за их малости), с учётом частного случая (в установившемся состоянии после переходного режима при ![]() ,
, ![]() ) после преобразований в операторной форме это уравнение (
) после преобразований в операторной форме это уравнение (![]() ) можно записать в следующем виде:
) можно записать в следующем виде:
![]()
Здесь ![]() , а DO
, MO
, NO
—полиномы от оператора р
такие, что:
, а DO
, MO
, NO
—полиномы от оператора р
такие, что:
![]() ;
;
![]() ;
;
![]() , где:
, где:
 ;
;
 ;
;
 .
.
Аналогично могут быть получены линеаризованные уравнения регулятора и устройства сравнения:
![]()
![]()
Исключая из системы уравнений ![]() ,
, ![]() ,
, ![]() переменные
переменные ![]() ,
, ![]() и опуская индекс вариации Δ, линеаризованная математическая модель системы примет вид:
и опуская индекс вариации Δ, линеаризованная математическая модель системы примет вид:
![]() (II΄)
(II΄)
где:
![]() ;
;
![]() ;
;
![]() ,
,
где a 0 – an , b 0 – bn , c 0 – cn однозначно определяются коэффициентами α, β и γ системы.
Тот же вид, но в развёрнутой форме:

 (II)
(II)
4.1.2 Математические модели систем управления в комплексной области
4.1.2.1 Преобразование Фурье
Абсолютно интегрируемые непрерывные функции f
(
t
)
, т.е. функции, удовлетворяющие условию  (1), можно представить в виде интеграла Фурье:
(1), можно представить в виде интеграла Фурье:
 (2)
(2)
 (3)
(3)
Это преобразование Фурье или комплексный спектр функции оригинала f ( t ) .
Существуют функции, для которых не выполняется неравенство (1), например: [1( t )] , e -α t , e α t , sin α t при α>0 , tn при n =1, 2, 3, … и др. Для них используют преобразование Лапласа, являющееся обобщением преобразования Фурье.
4.1.2.2 Преобразование Лапласа непрерывных функций
Рассмотрим f 1 ( t )= f ( t ) e - ct , c = const такая, что:
 (4)
(4)
При этом для существования этого интеграла от функции f(t) пришлось потребовать выполнения условия f
(
t
)=0 ![]() t
<0
.
t
<0
.
c > c 0 (c 0 — абсцисса абсолютной сходимости).
Для [1( t )] с0 =0
Для e -α t с0 =α
Для e α t с0 =-α
Дляsin α t с0 =0
Тогда получим  (5)
(5)
Это интеграл Лапласа или формула обращения в преобразовании Лапласа.
 (6)
(6)
f
(
t
)
![]() F
(
s
)
F
(
s
)
4.1.2.3 Нули и полюсы изображения F ( s )
F
(
s
)
— дробно рациональная функция. ![]()
Корни полиномов R ( s ) и Q ( s ) определяют свойства изображения или свойства этой функции.
4.1.2.3.1 Нули изображения F ( s )
Представим F ( s ) в следующем виде:
![]()
![]() , а
, а ![]() , значит F
(
s
)
имеет ноль кратности m
в точке
, значит F
(
s
)
имеет ноль кратности m
в точке ![]() .
.
4.1.2.3.2 Полюса изображения F ( s )
Полюса изображения F ( s ) — это корни полинома знаменателя Q ( s ) .
 , где
, где ![]() ,
,
а ![]() , т.е. изображение F
(
s
)
содержит полюс кратности n
при
, т.е. изображение F
(
s
)
содержит полюс кратности n
при ![]() .
.
На комплексной плоскости s нули обозначают “0”, а полюса “Х”.
4.1.2.4 Дискретное преобразование Лапласа
Данное преобразование применяется для решетчатых функций.
 (7)
(7)
 (7΄)
(7΄)
4.1.2.5 Z -преобразование
Введём новую комплексную переменную z = est , тогда (7) можно представить в следующем виде:
![]() ≜
≜  (8)!!!!
(8)!!!!
s=c+j∞
Выбрав c>
c
0
ряд (8) будет сходиться, и решетчатой функции будет соответствовать Z-преобразование. f
[
i
]
![]() F
(
z
).
F
(
z
).
Z-преобразование применяют и к непрерывным функциям. При этом, если для РФ f [ i ] прямая и обратная задачи однозначны, то для непрерывной функции задача определения оригинала f [ i ] по его изображению не однозначна.
4.1.2.6 Основные свойства преобразования Лапласа и Z -преобразования
| Свойства преобразования Лапласа | Свойства Z-преобразования |
1. Свойство линейности:
|
1. Свойство линейности:
|
2. Теорема о конечном значении: Если функция s ∙ F ( s ) является аналитической в правой полуплоскости и на мнимой оси, то
|
2. Теорема о конечном значении:
|
3. Теорема о начальном значении: Если |
3. Теорема о начальном значении:
|
4. Теорема сдвига в области вещественной переменной:
t - τ — запаздывание (по оси вправо). t + τ — упреждение (по оси влево). |
4. Теорема сдвига в области вещественной переменной:
|
5. Свойство дифференцирования: Если начальные условия нулевые, то |
|
6. Свойство интегрирования: при нулевых начальных условиях
|
|
7. Теорема свёртки:
|
Лекция №7. 04.03.2003
8. Задача определения оригинала функции по её изображению:
а) Непрерывные функции
Смотри формулу (5) из пункта № 4.1.2.2.
б) Дискретные математические модели (для решетчатых функций)
![]()
Так как F ( z ) дробно рациональная функция, то проще эту задачу решать так: разделив числитель на знаменатель, F ( z ) можно разложить в ряд Лорана по убывающим степеням, т.е.

Известно, что ![]() ≜
≜
f 0 , f 1 , f 2 , … — дискреты искомой решетчатой функции f [ iT ] .
4.1.2.7 Математические модели в комплексной области
4.1.2.7.1 Дискретные математические модели
Применяя к уравнению (Ⅰ) пункта № 4.1.1.1.2 Z-преобразование, с учётом свойств линейности и теоремы сдвига при нулевых начальных условиях получим:
![]()
![]() (I*
)
(I*
)
4.1.2.7.2 Непрерывные математические модели
Применяя к уравнению (Ⅱ) пункта № 4.1.1.2.2 преобразование Лапласа при нулевых начальных условиях, с учётом свойств линейности и дифференцирования получим:
![]()
![]() (II*
)
(II*
)
4.1.3 Математические модели систем управления в пространстве состояний
МПС (Метод Пространств Состояний) применяется для исследования многомерных систем и ориентирован на использование компьютера.
В основу МПС положено понятие многомерного фазового пространства (или пространства состояний), по осям которого откладываются обобщённые фазовые координаты системы (или переменные состояния).
Состояние системы — совокупность минимального количества параметров, полностью определяющих поведение динамической системы.
4.1.3.1 Непрерывные математические модели
Математическая модель системы при этом приводится к стандартному виду (или форме Коши):
 (1)
(1)
Система уравнений (1) — это уравнение состояния в развёрнутой форме.
Соответствующая системе уравнений (1) структура системы:
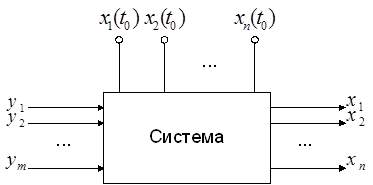
В матричной форме систему уравнений (1) можно записать в следующем виде:
![]() (2)
(2)
Здесь X , Y — вектора соответственно состояния и управления (смотри выше):
A — матрица системы; B — матрица управления.
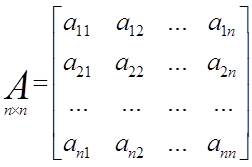

Уравнению состояния (2) соответствует следующая структура системы:

Система уравнений (1) и уравнение (2) соответствуют случаю, когда в качестве выходных переменных рассматриваются все переменные состояния.
В общем же случае количество выходных переменных зависит от рассматриваемой задачи и определяется линейной комбинацией переменных состояний ![]() и входных переменных (управляющих воздействий)
и входных переменных (управляющих воздействий) ![]() .
.
Поэтому уравнение состояния системы в развёрнутой форме примет следующий вид:
 (3)
(3)
Количество выходных переменных ![]() зависит от решаемой задачи.
зависит от решаемой задачи.
Системе уравнений (3) будет соответствовать следующая структура системы:

В матричной форме уравнение состояния системы выглядит так:
![]() (4)
(4)
Уравнению состояния (4) соответствует следующая структура системы:

Z
(
t
)
— вектор выхода 
С — матрица системы; D — матрица управления.


Пример 1.
Записать уравнения состояния в развёрнутой и матричной формах, составить схему (структуру) системы в переменных состояния непрерывной системы, математическая модель которой следующая:
![]() .
.
Решение.
1. Вводим переменные состояния:
![]() ,
, ![]() , …,
, …, ![]() .
.
2. Запишем уравнение состояния системы в развёрнутой форме Коши:

3. Запишем уравнение состояния в матричной форме:
![]()


4. Составляем структуру системы в переменных состояния:

Пример 2.
Смотри условие примера 1, но ![]() .
.
Решение.
1. Вводим переменные состояния:
![]() ,
, ![]() .
.
2. Запишем уравнение состояния системы в развёрнутой форме Коши:

3. Запишем уравнение состояния в матричной форме:
![]()


4. Составляем структуру системы в переменных состояния:

Пример 3.
По структуре системы в переменных состояния записать уравнения состояния в развёрнутой и матричной формах.

1.)

2.)

3.)

4.)

Лекция №14. 01.04.2003
![]() Передаточная функция:
Передаточная функция: 
![]() АФХ:
АФХ: 


 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | 0 |
| φ (ω) | 0 | –
|
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) 
 |
T — постоянная времени. ζ — коэффициент относительного демпфирования. η — угловая частота колебаний. |
6.4. Интегрирующее звено
![]() ММ:
ММ: ![]()
![]()
![]() Переходная функция:
Переходная функция:

![]() Передаточная функция:
Передаточная функция: 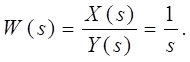
![]() АФХ:
АФХ: 

 |
||
| ω | 0 | +∞ |
| A( ω ) | ∞ | 0 |
| φ (ω) | –
|
–
|
![]() ЛЧХ: а)
ЛЧХ: а) ![]() б)
б) 
 |
Если подсистема состоит из ν
последовательно соединённых интегрирующих звеньев, то есть  , то наклон характеристики , то наклон характеристики 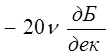 , а характеристика , а характеристика |
![]() будет проходить на уровне
будет проходить на уровне ![]() рад
.
рад
.
6.5 Дифференцирующее звено первого порядка
![]() ММ:
ММ: ![]() .
.
![]() Переходная функция:
Переходная функция: ![]()

![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]()
![]()
 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | ∞ |
| φ (ω) | 0 | +
|
![]() ЛЧХ: а)
ЛЧХ: а) ![]() б)
б) ![]()
 |
ЛЧХ этого звена является зеркальным отражением соответствующих ЛЧХ апериодического звена относительно оси частот. |
6.6 Дифференцирующее звено второго порядка
![]() ММ:
ММ: ![]()
![]() Переходная функция:
Переходная функция: 

![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]() .
.

 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | ∞ |
| φ( ω ) | 0 | + π |
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) 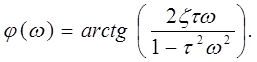
 |
ЛЧХ этого звена является зеркальным отражением соответствующих ЛЧХ колебательного звена относительно оси частот.
|
6.7 Идеальное дифференцирующее звено
![]() ММ:
ММ: ![]()
![]() Переходная функция:
Переходная функция: ![]()
![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]()

 |
||
| ω | 0 | +∞ |
| A( ω ) | 0 | ∞ |
| φ( ω ) | + |
+
|
АФХ этого звена является зеркальным отражением относительно вещественной оси АФХ интегрирующего звена.
![]() ЛЧХ: а)
ЛЧХ: а) ![]() б)
б) 
 |
ЛЧХ этого звена является зеркальным отражением соответствующих ЛЧХ интегрирующего звена относительно оси частот. |
Задание: реализовать такую типовую структуру в дискретной или аналоговой форме.
Во втором случае с помощью следующего простейшего четырёхполюсника:
 |
При R =0 математическая модель:
|

Получили структуру, состоящую из ТРЁХ типовых элементарных звеньев:
1) Усилительное звено с коэффициентом передачи T .
2) Идеальное дифференцирующее звено.
3) Апериодическое звено.
Следовательно, операция дифференцирования будет определяться в диапазоне частот, определяемом постоянной времени T .

Неминимально-фазовые типовые звенья.
6.8 Неустойчивое периодическое звено
![]() ММ:
ММ: ![]()
![]() Переходная функция:
Переходная функция: ![]()
 |
Примечание: получить экспериментально характеристики неминимально-фазовых звеньев не удаётся, это можно сделать только теоретически (формально). |
![]() Передаточная функция:
Передаточная функция: 
![]() АФХ:
АФХ: 

Таким образом, A ( ω ) неминимально-фазовых и минимально-фазовых звеньев совпадают, а φ(ω) — отличаются.
 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | ∞ |
| φ( ω ) | – π | –
|
АФХ этого звена является зеркальным отражением относительно мнимой оси АФХ устойчивого апериодического звена.
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) ![]()

Лекция №15. 02.04.2003
6.9 Неустойчивое колебательное звено
![]() ММ:
ММ: ![]() или
или ![]() .
.
![]() Переходная функция:
Переходная функция:

![]() Передаточная функция:
Передаточная функция: 
![]() АФХ:
АФХ: 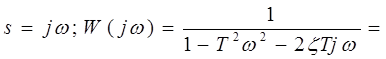


 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | 0 |
| φ( ω ) | 0 | + π |
АФХ этого звена является зеркальным отражением относительно вещественной оси АФХ устойчивого колебательного звена.
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) 
 |
 |
6.10 Неминимально-фазовое дифференцирующее звено первого порядка
![]() ММ:
ММ: ![]() .
.
![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]() .
.
![]()
 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | ∞ |
| φ( ω ) | π | + |
АФХ этого звена является зеркальным отражением относительно мнимой оси АФХ минимально-фазового дифференцирующего звена первого порядка.
![]() ЛЧХ: а)
ЛЧХ: а) ![]() б)
б) ![]()
 |
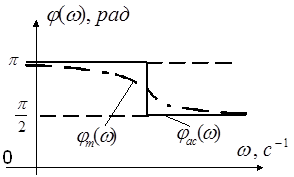 |
6.11 Неминимально-фазовое дифференцирующее звено второго порядка
![]() ММ:
ММ: ![]()
![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]() .
.

 |
||
| ω | 0 | +∞ |
| A( ω ) | 1 | ∞ |
| φ( ω ) | 0 | – π |
АФХ этого звена является зеркальным отражением относительно вещественной оси АФХ минимально-фазового дифференцирующего звена первого порядка.
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) 
 |
 |
6.12 Звено чистого запаздывания
Свойства звена чистого запаздывания (ЗЧЗ): 
|
1) Рецептор зрительного анализатора человека. 2) Любой канал связи. 3) Давление в трубопроводе. |
![]() ММ:
ММ: ![]()
![]() Передаточная функция:
Передаточная функция: ![]()
![]()
![]() АФХ:
АФХ: ![]()
![]()

![]() ЛЧХ: а)
ЛЧХ: а) ![]() б)
б) ![]()

6.13 Звено чистого запаздывания
![]() ММ:
ММ: ![]()
![]() Передаточная функция:
Передаточная функция: ![]()
![]() АФХ:
АФХ: ![]()
![]()

Раздел 7. Анализ устойчивости систем
В замкнутой динамической системе выходной сигнал не может появиться на входе мгновенно для противодействия входному сигналу. Это обусловлено тем, что энергия в подсистемах не может изменяться мгновенно, то есть существует запаздывание. Энергия колеблется относительно некоторого уровня и при определённых условиях система из источника подавления колебаний становится их генератором, то есть оказывается неустойчивой.
7.1 Понятие устойчивости по А. М. Ляпунову
(1892 год.)
Рассмотрим непрерывную многомерную систему в свободном движении, математическая модель которой следующая:
![]() … (1)
… (1)
Здесь Xi — любая линейная или нелинейная функция, а xi — обобщённая фазовая координата или переменная состояния системы n-мерного порядка (фазовые координаты).
В n-мерном фазовом пространстве (пространстве состояний) в фиксированный момент времени xi определяют состояние системы в виде точки с соответствующими координатами, например, при n =3 :
 |
M(x) — изображающая точка. В переходном режиме изображающая точка описывает некоторую траекторию, которую назовём фазовой . |
Проекции вектора скорости изображающей точки на оси — левые части уравнений (1), следовательно, о поведении системы в переходном режиме можно судить по правым частям уравнений (1).
Так, например, если n =2 , имеем фазовую плоскость:

Исключая из этой системы время t
, получим: 
Интегрируя это уравнение, получим семейство фазовых траекторий (фазовый портрет) системы, каждая из которых соответствует определённому значению постоянной интегрирования.
Фазовый портрет полностью определяет основные свойства свободного движения системы.
 |
Пусть в начальный момент времени изображающая точка M
(
xi
0
)
при t
=0
начала двигаться по некоторой невозмущённой фазовой траектории |
Таким образом, движение системы устойчиво, если при сдвиге начального положения изображающей точки на величину не более малой положительной величины ![]() (*) возмущённое движение в последующие моменты времени будет отличаться от невозмущённого на величину не более сколь угодно малой величины
(*) возмущённое движение в последующие моменты времени будет отличаться от невозмущённого на величину не более сколь угодно малой величины ![]()
![]() (**).
(**).
В противном случае движение системы не устойчиво.
Если при этом выполняется условие ![]() (***), то движение асимптотически устойчиво. Следовательно, по Ляпунову оценивается устойчивость системы при достаточно малых начальных отклонениях. Линейная стационарная система, устойчивая “в малом”, будет устойчива и “в большом”.
(***), то движение асимптотически устойчиво. Следовательно, по Ляпунову оценивается устойчивость системы при достаточно малых начальных отклонениях. Линейная стационарная система, устойчивая “в малом”, будет устойчива и “в большом”.
7.2 Необходимые и достаточные условия устойчивости линейных стационарных систем
Пусть известна математическая модель системы, описывающая свободное движение системы в виде однородного дифференциального уравнения:
![]() (1)
(1)
или разностного уравнения
![]() (1΄)
(1΄)
и пусть x
— это отклонение интересующей нас переменной от её значения в равновесном режиме. Тогда система будет устойчива
, если выполняется условие ![]() (2)
(2)
или ![]() (2΄)
(2΄)
При каких условиях выполняется равенство (2)?
Уравнениям (1) и (1΄) соответствуют характеристические уравнения:
![]() … (3)
… (3)
![]() … (3΄)
… (3΄)
Если корни si
уравнения (3) различны, то решение уравнения (1) может быть записано следующим образом  .
.
В общем случае корни являются комплексными si =α i + j β i .

1) Если α
k
>0
A
→∞ ![]() система не устойчива.
система не устойчива.
2) Если α
k
<0
A
→0 ![]() система устойчива.
система устойчива.
3) Если α
k
=0
A
=
ck
=
const
![]() система нейтрально устойчива.
система нейтрально устойчива.
Следовательно, для устойчивости линейной непрерывной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, то есть располагались в левой полуплоскости плоскости S .
Можно показать, что для устойчивости дискретной линейной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения (3΄) zi были: | zi |<1 … (!!)
Лекция №8. 05.03.2003
4.1.3.1.1 Решение уравнения состояния
![]() (5)
(5)
Пусть при t = t 0 X ( t 0 )= X 0 (начальные условия). Из теории дифференциальных уравнений известно, что решение уравнения (5) при известных начальных условиях может быть получено в следующем виде:
![]() (6)
(6)
где M ( t ) — фундаментальная или переходная матрица.
Решение уравнения (5) можно записать и в виде ряда Тейлора:
 (7)
(7)
Производные в формуле (7) можно определить из уравнения (5):
![]()


т.е. ![]() (8)
(8)
Здесь  (9)
(9)
е At — МАТРИЦИАНТ.
Можно сказать, что решение неоднородного уравнения состояния ![]() имеет вид:
имеет вид:
 (10)
(10)
4.1.3.2 Дискретные математические модели многомерной системы
Рассмотрим многомерный импульсный фильтр:

1 — непрерывная часть системы;
4 — формирователи.
В случае экстраполятора нулевого порядка (Э0П) управляющие сигналы yp ( t ) , действующие на непрерывную часть системы, будут кусочно-постоянными, т.е. yp ( t )= yp [ iT ], iT ≤ t ≤ ( i +1) T в скалярной форме или Y ( t )= Y [ iT ] при iT ≤ t ≤ ( i +1) T в векторной.
Рассмотрим уравнение (10) при следующих условиях:
1) t 0 = iT — начальные условия.
2) ( iT , t ) — интервал интегрирования.


![]()
В частности, при t =( i +1) T :

Таким образом:
![]() (11)
(11)
Это уравнение состояния многомерной дискретной системы.
Здесь:
 (12)
(12)
е AT — МАТРИЦИАНТ.
 (13)
(13) ![]() (14)
(14)
В развёрнутой форме уравнение состояния примет вид:
 (III)
(III)
Пример 4.
Определить уравнение состояния многомерной импульсной системы с Э0П. Математическая модель непрерывной части известна:
![]()
1. Составим уравнение состояния непрерывной части системы:
![]() ,
, ![]() , тогда
, тогда 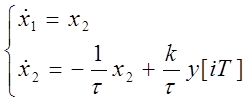



2.

3.


![]()
![]()





4.


5.

6. Запишем уравнение состояния:
![]()

 (III΄)
(III΄)
Лекция №9. 11.03.2003
Раздел 5. Основные характеристики систем
5.1. Передаточная функция
5.1.1 Непрерывные системы
Из выражения (II* ) при f ( t )=0 следует
 (1)
(1)
Передаточная функция W ( s ) — отношение преобразования Лапласа величины на выходе системы X ( s ) к величине на входе системы Y ( s ) при нулевых начальных условиях.
Основные свойства передаточной функции:
1) Это дробно-рациональная функция.
2) Коэффициенты полиномов числителя и знаменателя — вещественные числа.
3) Невещественные нули и полюса передаточной функции являются комплексно сопряжёнными.
4) Все полюса передаточной функции устойчивой системы располагаются в левой полуплоскости плоскости S.
Различают несколько видов ПФ:
Рассмотрим непрерывную линейную стационарную систему, математическая модель которой следующая:
 |
|

Применяя к этой системе преобразование Лапласа, при нулевых начальных условиях получим:
 |
|
![]() ПФ системы в разомкнутом состоянии.
ПФ системы в разомкнутом состоянии.
Отключим от элемента сравнения главную обратную единичную связь ![]() уравнение
уравнение ![]() вырождается, а уравнение
вырождается, а уравнение ![]() принимает вид:
принимает вид:
![]()
Подставляя в уравнение ![]() , получим:
, получим:
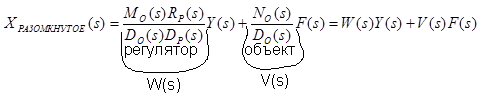
а) ![]() — ПФ разомкнутой системы по управляющему воздействию.
— ПФ разомкнутой системы по управляющему воздействию.
б) ![]() — ПФ разомкнутой системы по возмущающему воздействию.
— ПФ разомкнутой системы по возмущающему воздействию.
![]() ПФ системы в замкнутом состоянии.
ПФ системы в замкнутом состоянии.
Подключим главную обратную единичную связь к элементу сравнения. Рассмотрим систему уравнений ![]() . Исключая из этой системы переменные E
(
s
)
и R
(
s
)
, получим:
. Исключая из этой системы переменные E
(
s
)
и R
(
s
)
, получим:
![]()
а) возмущение отсутствует f ( t )=0:
![]() — ПФ замкнутой системы по управляющему воздействию.
— ПФ замкнутой системы по управляющему воздействию.
б) управление отсутствует y ( t )=0:
![]() — ПФ замкнутой системы по возмущающему воздействию.
— ПФ замкнутой системы по возмущающему воздействию.
Исключая из системы уравнений ![]() R
(
s
)
и X
(
s
)
, получим:
R
(
s
)
и X
(
s
)
, получим:
![]()
Если f
(
t
)=0
, то ![]() — ПФ по ошибке относительно управляющего воздействия.
— ПФ по ошибке относительно управляющего воздействия.
Если не единственная обратная связь, то смотри методические указания.
![]() ПФ астатических систем.
ПФ астатических систем.
Известно, что ![]()

![]() (*)
(*)
Условие (*) выполняется, когда ![]() , где Y
0
(0)=
const
≠0
.
, где Y
0
(0)=
const
≠0
.
Пример.

![]()
![]()
![]() система будет астатичной, если её ПФ имеет простой/однократный нуль при s
=0
система будет астатичной, если её ПФ имеет простой/однократный нуль при s
=0
т.к.  и если
и если  , а
, а ![]()

Если W ( s ) (ПФ разомкнутой системы) имеет хотя бы один простой полюс при s =0 .
5.2 Переходная функция
Переходная функция h ( t ) — реакция системы на единичное ступенчатое воздействие.
Эта функция определяет качество регулирования системы.
Основными оценками качества регулирования являются следующие параметры:

![]() Пример на странице 29 методических указаний.
Пример на странице 29 методических указаний.
h ( t ) можно определить следующим образом:
1) по ММ системы в области вещественной переменной t (численно /стр. 28/).
2) по ММ в области комплексной переменной
Рисунок |
|
5.3 Импульсная переходная функция (функция веса)
Так же, как и h ( t ) , ИПФ k ( t ) является основной характеристикой системы во временной области. Это реакция системы на δ-функцию.
 , !!!
, !!!
так как ![]() .
.
Лекция №10. 12.03.2003
Основные свойства импульсной переходной функции:
1) ИПФ и ПФ являются преобразованием Лапласа друг от друга. Задание одной из них достаточно для задания другой.
2)  — условие устойчивости.
— условие устойчивости.
3) k ( t )=0 для любого t <0 — условие физической реализуемости.
4)  .
.
5) Если y
(
t
)
непрерывная и ограниченная функция и элементарное управляющее воздействие yi
(
t
)
вызывает реакцию ![]() , то с учётом суперпозиции:
, то с учётом суперпозиции:

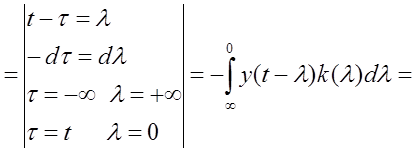
 |
— интеграл Дюамеля. — определяет реакцию системы по элементарному воздействию (известной импульсной функции.) |
5.4 Дискретная передаточная функция
5.4.1 Дискретная передаточная функция импульсного одномерного фильтра

Пусть известна импульсная переходная функция приведённой непрерывной части КП ( t ) , то есть реакцию на единичную импульсную решетчатую функцию.

Определим реакцию импульсного фильтра на дискретную последовательность (решетчатую функцию):
U [ mT ], m =0, 1, …, i — на входе. x ( t ) — ?
| Дискрета | Реакция | ||
U[0T] U[1T] … U[mT] |
U[0T] КП (t) U[T] КП (t-T) … U[mT] КП (t-mT) |
элементарные реакции |

Непрерывная часть сглаживает импульсы, но мы хотим выделить дискреты:
t
=
iT


Применим Z-преобразование:
 , тогда с учётом теоремы свёртки получим: X
(
z
)=
W
П
(
z
)
U
(
z
);
U
(
z
)=
Z
{
U
[
i
]}.
, тогда с учётом теоремы свёртки получим: X
(
z
)=
W
П
(
z
)
U
(
z
);
U
(
z
)=
Z
{
U
[
i
]}.
![]()
![]() ≜
≜ — ДПФ импульсного фильтра.
— ДПФ импульсного фильтра.
По аналогии с непрерывными системами: ![]() (отношение Z-преобразования сигнала на выходе фильтра к Z-преобразованию входного сигнала при нулевых обратных условиях).
(отношение Z-преобразования сигнала на выходе фильтра к Z-преобразованию входного сигнала при нулевых обратных условиях).
Так как  , то на практике очень удобна следующая формальная запись:
, то на практике очень удобна следующая формальная запись: ![]() !!!
!!!
то есть ДПФ равна Z-преобразованию такой функции оригинала, преобразование Лапласа которой равно W ( s ) .
Пример № 1:


5.4.2 Дискретная передаточная функция импульсной системы с экстраполятором нулевого порядка
Структура системы приведена на Рисунке № !.
Можно показать, что ДПФ такой системы в разомкнутом состоянии (когда убираем главную обратную связь) определяется по следующей формуле:
 !!!!
!!!!
W ( s ) — передаточная функция непрерывной части системы.
Пример № 2.
Определить ДПФ микропроцессорной (импульсной) системы (Рисунок № !), непрерывная часть которой следующая:

Решение:
1) 
2) — раскладываем на простые дроби.
— раскладываем на простые дроби.
3) 

5.4.3 Дискретная передаточная функция многомерной системы
Задачу определения ДПФ для многомерного случая удобно решать Методом Пространств Состояний:
Рассмотрим алгоритм решения этой задачи для простейшего одномерного случая:

 (смотри связь между ПФ и дифференциальным уравнением)
(смотри связь между ПФ и дифференциальным уравнением)
Известно, что решение этого дифференциального уравнения первого порядка: x ( t 0 )= x 0

При U ( t )= U [ iT ], iT ≤ t < ( i +1) T интегрируя в пределах ( iT , t ) :

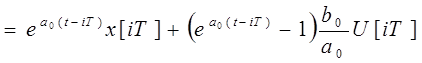 .
.
t =( i +1) T
 .
.
Применяя к этому выражению Z-преобразование с начальными нулевыми условиями, с учётом теоремы сдвига и свойств линейности:

ММ многомерной системы приведена выше (смотри систему уравнений (III)). Применяя к этой системе Z-преобразование с нулевыми начальными условиями, с учётом свойств линейности получим:
 (III*
)
(III*
)
Эта ММ позволяет определить матричную дискретную передаточную функцию ![]() , элементы которой рассчитываются по следующим формулам:
, элементы которой рассчитываются по следующим формулам:
 (1)
(1)
Здесь  (2)
(2)
Определитель ![]() можно получить из определителя (2) путём замены q
-
столбца следующим столбцом:
можно получить из определителя (2) путём замены q
-
столбца следующим столбцом: ![]()
5.4.3.1 Пример № 3
По системе линейных разностных уравнений, полученных в примере (III′), определить дискретные передаточные функции от управления y к координатам x 1 и x 2 .
![]()
![]()

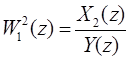
Лекция №11. 18.03.2003
Решение:
1) 
 2)
2) 

3) 
4) 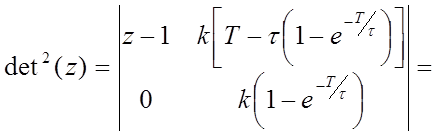

5) 
5.4.3.2 Численный расчёт дискретных передаточных функций многомерных систем
Если известно уравнение состояния ![]() то можно получить уравнение состояния многомерной импульсной системы
то можно получить уравнение состояния многомерной импульсной системы ![]() . При этом матрицы G
, H΄
, H
определяются численно в виде рядов с использованием матриц А
и В
по приведённым выше формулам.
. При этом матрицы G
, H΄
, H
определяются численно в виде рядов с использованием матриц А
и В
по приведённым выше формулам.
Реализация алгоритмов определения элементов ![]() требует операции раскрытия определителей (смотри Пример № 3). Эту задачу можно решить или классически (по известным методам), или численно. При высоком порядке системы более эффективны численные методы Фадеева, Крылова, Леверрье.
требует операции раскрытия определителей (смотри Пример № 3). Эту задачу можно решить или классически (по известным методам), или численно. При высоком порядке системы более эффективны численные методы Фадеева, Крылова, Леверрье.
Рассмотрим метод Фадеева:
Во-первых , определитель системы det ( z ) (2) является характеристическим многочленом матрицы G , следовательно:
![]()
Необходимо найти коэффициенты этого полинома: ![]() .
.
Алгоритм расчёта коэффициентов по Фадееву:
1 этап: 1 шаг: 2 шаг: 3 шаг: |
2 этап: 1 шаг: 2 шаг: 3 шаг: |
Предпоследний этап: 1 шаг: 2 шаг: 3 шаг: |
Последний этап: 1 шаг: 2 шаг: 3 шаг: |
Пример № 4.
Рассмотрим систему второго порядка: 
Поиск методом Фадеева:
1)  , в котором неизвестны a
1
и a
0
.
, в котором неизвестны a
1
и a
0
.
2) а)  б)
б) ![]()
в) 
3) а) 
 б)
б) 
![]() в) Контроль:
в) Контроль: ![]()
Во-вторых
, ![]() отличен от определителя системы (III*
)
отличен от определителя системы (III*
)
Для расчёта коэффициента этого определителя можно использовать найденные значения коэффициентов ai .
Пусть  (3)
(3)
![]()
![]() (4)
(4)
Если подать на вход исходной системы (III* ) какой-либо известный входной сигнал yp [ iT ], i = 0, 1, 2, … при нулевых остальных входных сигналах y 1 [ iT ]= y 2 [ iT ]=…= yp -1 [ iT ]= yp +1 [ iT ]=…=0 и при нулевых начальных условиях x 1 [0]= x 2 [0]=…=0 , то путём непосредственных расчётов по системе (III* ) (смотри задачу семинара №2) можно последовательно получить значения x [ T ], x [2 T ], …, x [ iT ].
Если подать тот же самых сигнал Yp на вход разностного уравнения (4) при нулевых начальных условиях (x [0]= x [– T ]=…=0 ), то дискреты xq [ iT ] уравнения (4) совпадут с сигналами xq [ iT ] вектора X [ iT ] , расcчитанного по уравнению (III* ).
Тогда можно показать, что:
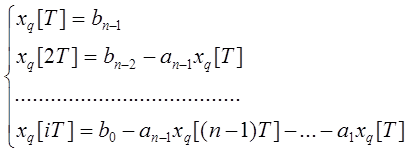
при входном сигнале  (*)
(*)
 (5)
(5)
Пример № 5.
Рассмотрим систему второго порядка, своего рода (III* ) при n =2 .

Для системы второго порядка определить дискретную передаточную функцию  при нулевых начальных условиях.
при нулевых начальных условиях.
Решение:
1) det ( z ) определён в примере № 4.
2) Составляем разностное уравнение p =2, n =2, q =1 :

 (4΄)
(4΄)
3) Рассчитываем переходный процесс по исходной системе (III* ) при n =2 :
i =0

(смотри условие (*)).
![]()
i = 1


4) Определяем коэффициенты:
![]()
![]()
![]() .
.
Лекция №12. 25.03.2003
5.5 Частотные характеристики
5.5.1 Непрерывные системы
Рассмотрим ММ стационарной непрерывной системы:
![]() (1)
(1)
Пусть ![]()
![]()
На основе формулы Эйлера (![]() ):
):
 , начальные условия нулевые.
, начальные условия нулевые.
При нулевых начальных условиях решение уравнения (1) можно получить в виде двух слагаемых x ( t )= x 1 ( t )+ x 2 ( t ) .
При этом с учётом принципа суперпозиции: x
1
(
t
)![]() y
1
(
t
)
, x
2
(
t
)
y
1
(
t
)
, x
2
(
t
)![]() y
2
(
t
)
.
y
2
(
t
)
.
Найдём x 1 ( t ) :
 , где W
— пока неизвестная и не зависящая от времени функция.
, где W
— пока неизвестная и не зависящая от времени функция.
Подставляя в уравнение (1) x 1 , y 1 и их соответствующие производные, получим:
![]()
![]()
 … (2)
… (2)
![]() Комплексно-частотную характеристику системы
Комплексно-частотную характеристику системы ![]() можно получить передаточной функции путём замены переменной
можно получить передаточной функции путём замены переменной ![]() (смотри уравнение (1) раздела 5.1.1.).
(смотри уравнение (1) раздела 5.1.1.).
Комментарий:
![]() , … (3)
, … (3)
|
 |
Здесь: ![]()
![]()
![]()
![]()
Смотри методические указания, страница 18.

![]() , … (4)
, … (4)
где ![]() — Амплитудно-частотная характеристика (АЧХ).
— Амплитудно-частотная характеристика (АЧХ).
 — Фазово-частотная характеристика (ФЧХ).
— Фазово-частотная характеристика (ФЧХ).
Пример смотри в методических указаниях, рисунки 11 и 12.
При изменении ![]() конец вектора
конец вектора ![]() описывает кривую, называемую АФХ — амплитудно-фазовая характеристика или Катографом Найквиста (Рисунок 21 методических указаний).
описывает кривую, называемую АФХ — амплитудно-фазовая характеристика или Катографом Найквиста (Рисунок 21 методических указаний).
Физический смысл частотной характеристики: частотная характеристика — результат анализа вынужденного движения линейной стационарной системы при гармоническом воздействии.
Таким образом,  .
.
Аналогично можно определить составляющую
 воздействия y
2
(
t
)
.
воздействия y
2
(
t
)
.
То есть  .
.
![]() … (5)
… (5)
Таким образом, если на входе рассматриваемой системы действует гармонический входной сигнал, то выходной сигнал будет также гармоническим (Формула (5)) и отличающимся от входного по амплитуде в ![]() раз, а по фазе на
раз, а по фазе на ![]() . Здесь
. Здесь ![]() — АЧХ, а
— АЧХ, а ![]() — ФЧХ.
— ФЧХ.
Замечание № 1:
Так как АФХ симметрична относительно вещественной оси ![]() для положительных и отрицательных значений
для положительных и отрицательных значений ![]() , то обычно ограничивают диапазон изменения
, то обычно ограничивают диапазон изменения ![]() :
: ![]() .
.
Замечание № 2:
Иногда вместо обычной АФХ ![]() рассматривают нормированную АФХ
рассматривают нормированную АФХ
![]() такую, что
такую, что ![]() , где
, где ![]() , а
, а ![]() — порядок астатизма системы, или обратную АФХ
— порядок астатизма системы, или обратную АФХ
 , или обратно нормированную АФХ
, или обратно нормированную АФХ
![]() .
.
Замечание № 3:
Очень часто вместо АФХ ![]() используют Логарифмическую Частотную Характеристику (ЛЧХ).
используют Логарифмическую Частотную Характеристику (ЛЧХ).
а) ![]() — ЛАЧХ.
— ЛАЧХ.
б)  — ЛФЧХ.
— ЛФЧХ.
По оси абсцисс соответственно отмеряются либо ![]() , либо
, либо ![]() .
.
Примеры в методических указаниях — рисунки 12, 22, 25 а)
Примеры нормированных ЛЧХ ![]() — рисунки 23 и 25 б).
— рисунки 23 и 25 б).
5.5.2 Дискретные системы
Анализ вынужденного движения импульсной системы на воздействие y [ iT ]= Ycos [ω iT +φ0 ] , значение которого в дискретные моменты времени образуют гармоническую решетчатую последовательность, определяет частотные характеристики системы:
Частотная характеристика — ![]()
АФХ дискретной системы может быть получена из ДПФ путём замены переменной ![]() , т.е.
, т.е. ![]()
![]()
![]()
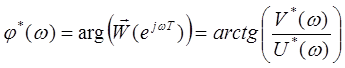
Особенности АФХ:
![]() — периодическая функция с периодом
— периодическая функция с периодом ![]() , поэтому её можно определить для любого интервала частот указанного периода (
, поэтому её можно определить для любого интервала частот указанного периода (![]()
![]() )
)
ЛЧХ дискретных систем, в отличие от ЛЧХ непрерывных систем, не обладают асимптотическими свойствами.
Для восстановления указанного свойства используют билинейное W-преобразование  , а также относительные (
, а также относительные (![]() ) и абсолютные (
) и абсолютные (![]() ) псевдочастоты.
) псевдочастоты.

 , т.е.
, т.е.
 и
и 
Таким образом, при  имеем:
имеем: ![]() !
!
И при  имеем:
имеем: ![]() !!
!!
5.6 Основные правила преобразования структур линейных стационарных детерминированных систем
5.6.1 Непрерывные системы
![]()
![]()
![]()
![]()
![]()

![]()
Лекция №13. 26.03.2003
![]() Правило исключения отрицательной обратной связи.
Правило исключения отрицательной обратной связи.
 |
 |
![]() Узлы
Узлы
| а) |  |
 |
 |
| б) |  |
 |
 |
![]() Элементы суммирования
Элементы суммирования
| а) |  |
 |
 |
| б) | 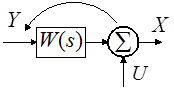 |
 |
 |
5.6.2 Дискретные системы
![]()
 |
 |
![]()
![]()

![]()
![]()

![]()
![]()



![]()

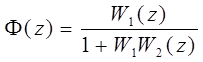
![]()
 |
 |
Для нелинейных или нестационарных систем будет по другому.
Раздел 6. Типовые элементарные структуры (звенья) системы управления
В структуре системы можно выделить элементарные подсистемы с определёнными, только им присущими, характеристиками.
Рассмотрим передаточную функцию непрерывной системы:

при этом возможны следующие случаи:
1) Если ![]() (вещественный корень), то
(вещественный корень), то

2) Если существует два комплексно сопряжённых корня ![]() ,
, ![]() таких, что
таких, что ![]() и
и ![]() , тогда:
, тогда:
![]()

 , где
, где  и
и 
3) Еслиsi =0 , s–si =s .
Таким образом передаточную функцию системы можно представить в следующем виде:

следовательно, в структуре системы в общем случае можно выделить одиннадцать типовых элементарных структур (звеньев).
Звенья со знаком “+” называют минимально-фазовыми, а со знаком “–”, кроме ![]() , неминимально-фазовыми (их четыре). К неминимально-фазовым относят также звено чистого запаздывания, а также инвертирующее звено.
, неминимально-фазовыми (их четыре). К неминимально-фазовым относят также звено чистого запаздывания, а также инвертирующее звено.
6.1 Усилительное звено
![]() — Типовая Элементарная Структура.
— Типовая Элементарная Структура.
![]() ММ: x
=
ky
.
ММ: x
=
ky
.
![]() Переходная функция:
Переходная функция:

![]() Передаточная функция:
Передаточная функция: 
![]() АФХ:
АФХ: ![]()

![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) ![]()

6.2 Апериодическое звено
![]() ММ:
ММ: ![]() в дальнейшем k
=1
.
в дальнейшем k
=1
.
![]() Переходная функция:
Переходная функция: ![]()

![]() Импульсная переходная функция:
Импульсная переходная функция: 

![]() Передаточная функция:
Передаточная функция: 
![]() АФХ:
АФХ: 

 |
||
| ω | 0 | ∞ |
| A( ω ) | 1 | 0 |
| φ (ω) | 0 | –
|
![]() ЛЧХ: а)
ЛЧХ: а) ![]()
б) ![]()
 |
1) Tω <1 , T 2 ω 2 <<1 . При этом L ас =0 — низкочастотная асимптота (а — б). 2) Tω >1 , T 2 ω 2 >>1 . При этом L ас = –20 lgTω — высокочастотная асимптота (в — г). При изменении частот в 10 раз: ω 1 =1 c –1 ; ω 2 =10 c –1 . L ас 1 =–20lgT; L ас 2 =–20lgT–20 .
|
![]()
6.3 Колебательное звено
![]() ММ:
ММ: ![]()
![]() Переходная и импульсная переходная функции:
Переходная и импульсная переходная функции:

где  — угловая частота колебаний.
— угловая частота колебаний.

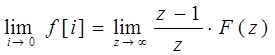


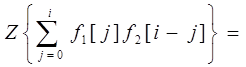










 .
.