| Скачать .docx |
Курсовая работа: Решение задачи разгона установившегося движения и замедление судна в процессе его эксплуатации
Нижегородский Государственный Технический Университет
Кафедра: "Прикладная математика"
Курсовая работа по информатике
Тема: "Решение задачи разгона установившегося движения и замедление судна в процессе его эксплуатации ("Беларусь-В")"
Выполнил:
Студент
Ткачева Е.С.
Проверила:
Жданова О.С.
Нижний Новгород
2009 г .
Оглавление
1. Постановка задачи и её математическая модель
2. Методика и алгоритмы решения задач
3. Первая модельная задача
4. Вторая модельная задача
5. Третья модельная задача
6. Сводная таблица результатов и выводы
1. Постановка задачи и её математическая модель.
1.1 Общая задача описания динамики разгона (торможения) судна
Из курса теоретической механики известно, что в соответствии с принципом Даламбера неустановившееся движение тела описывается вторым законом Ньютона. Поскольку в данной задаче рассчитывается движение лишь в направлении одной из осей координат, то достаточно записать уравнения движения в проекции на ось Х и решать его относительно скорости V и пройденного по этой координате пути S .
1.2 Физическая и математическая модели неустановившегося движения судна
Основным уравнением задачи в этом случае является уравнение второго закона Ньютона в проекции на ось координат X .
ma = F (1)
Здесь:
m – масса тела (судна);
а = dV / dt – ускорение тела;
F – сумма всех сил, действующих на судно, в проекции на ось X .
Равнодействующая сила F складывается из двух сил:
R – сопротивление движению судна;
Т – тяга движения (как правило, гребного винта).
Из физических соображений понятно, что сопротивление R зависит от скорости движения (чем больше скорость V , тем больше сопротивление R ) и направлена против скорости V , т.е. в отрицательном направлении оси X . Тяга, создаваемая гребным винтом, также зависит от скорости судна, но действует в противоположном направлении силе сопротивления R , т.е. направлена в положительном направлении оси X . Во время стоянки судна V =0 b R ( V )=0.
Тяга, создаваемая гребным винтом, также зависит от скорости движения судна, но действует в противоположном силе сопротивления R направлении, т.е. направлена противоположном направлении оси Х.
С учетом сказанного, уравнение (1) можно записать в виде:
![]() (2)
(2)
Таким образом, получено обыкновенное дифференциальное уравнение 1-го порядка относительно скорости движения судна V .
Для определения пройденного за время "разгона" пути S к этому уравнению (2) необходимо добавить уравнение dS / dt = V , являющееся определением понятия – "скорость". Математическая модель задачи записывается в виде системы из двух дифференциальных уравнений 1-го порядка, записанных в каноническом виде:
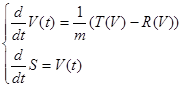 (3)
(3)
Здесь функции R ( V ) и T ( V ) являются заданными и находятся по испытаниям моделей судна и гребного винта. Как правило, эти функции задаются либо графически, либо таблично.
Для решения системы уравнений (3) необходимо задать начальные условия. Обычно они задаются в виде t =0 или V = Vn .
2. Методика и алгоритмы решения задачи
2.1 Формирование функций исходных данных
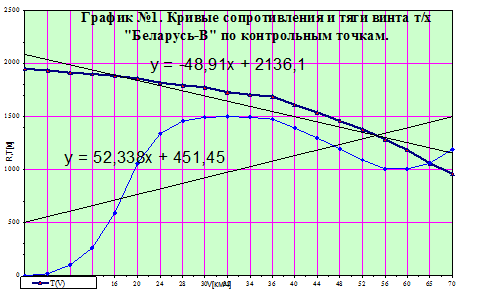
В курсовой работе исходными данными являются функции R ( V ) и T ( V ), которые представлены в графическом виде. Решением данной задачи является снятие контрольных точек с графиков ( R ( V ) – 16-20 точек и T ( V ) – 8-10 точек) включая первую и последнюю и заполнение таблиц исходных данных (расчёты производятся в системе СИ).
2.2 Аппроксимация исходных данных
По сформированным таблицам этих функций необходимо:
- выбрать класс аппроксимирующей функции (если выбран полином, то необходимо выбрать его степень исходя из вида кривой по характерным точкам, выбранным из контрольных);
- определить коэффициент аппроксимации;
- рассчитать и вывести на дисплей графики аппроксимирующих функций.
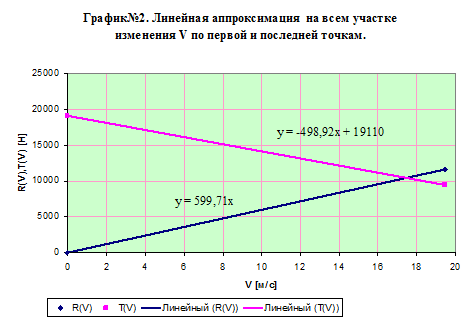
Модельная задача №1. Линейная аппроксимация исходных функций R ( V ) и T ( V ) на всём участке по первой и последней точкам.
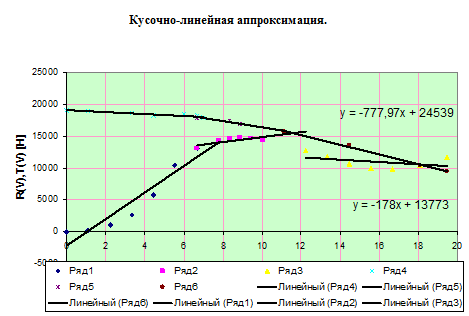
Модельная задача №2. Кусочно-линейная аппроксимация исходных функций R ( V ) (3 участка) и функции T ( V ) (2 участка).
Модельная задача №3. Кусочо-нелинейная аппроксимация исходных функций R ( V ) (не менее 3 участков) и T ( V ) на всём участке. Подобрать оптимальный вариант аппроксимирующих функций с учётом неразрывности функции на границах участков.
2.3 Эталонное аналитическое решение системы дифференциальных уравнений
Для отладки программы решения общей (при произвольных R ( V ) и T ( V )) системы (3) целесообразно задать эти функции в виде полиномов 1-й степени.
![]()
![]() (4)
(4)
Здесь коэффициенты аппроксимации![]() находятся по методу интерполяции по первой и последней точкам.
находятся по методу интерполяции по первой и последней точкам.
Подставляя соотношения (4) в систему (3) получим:
![]() или
или![]() (5)
(5)
где F 0= T 0- R 0, F 1= T 1- R 1.
Это простейшее дифференциальное уравнение с разделяющимися переменными:
![]() (6)
(6)
Решение этого уравнения:
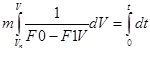
Здесь начальные условия входят в пределы интегрирования. Вычисляя интегралы, получаем:
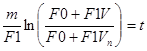
Потенцируя, получаем:
![]()
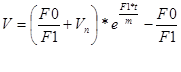
Это и есть точное решение уравнения (6). При t =0 имеем V = VH , то есть начальное условие выполнено автоматически. При разгоне коэффициент F 1<0 и при ![]() получаем:
получаем:
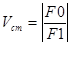 при F 1<0 и при
при F 1<0 и при ![]() (7)
(7)
При отладке программы в общем случае получаемое численное решение с линейными аппроксимациями T ( V ) и R ( V ) сравнивается с точным для проверки правильности алгоритма решения. На этом этапе расчёта строится график зависимости V = V ( t ) и график численного решения уравнения (6). Он совпадают с заданной точностью.
2.4 Вычисление кинетической энергии
Для расчёта кинетической энергии затрачиваемой на разгон судна используется известное соотношение
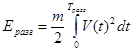
Такой же расчёт необходимо произвести для задачи торможения.
Вычисление интеграла производится одним из численных методов на основании результатов, полученных в третьей модельной задаче.
Контрольные точки с графиков
| V | R(V) | T(V) | ||||
| км/ч | м/с | кг | Н | кг | Н | |
| 1 | 0 | 0 | 0 | 0 | 1950 | 19110 |
| 2 | 4 | 1,1112 | 20 | 196 | 1940 | 19012 |
| 3 | 8 | 2,2224 | 100 | 980 | 1915 | 18767 |
| 4 | 12 | 3,3336 | 260 | 2548 | 1900 | 18620 |
| 5 | 16 | 4,4448 | 590 | 5782 | 1885 | 18473 |
| 6 | 20 | 5,556 | 1060 | 10388 | 1860 | 18228 |
| 7 | 24 | 6,6672 | 1340 | 13132 | 1820 | 17836 |
| 8 | 28 | 7,7784 | 1460 | 14308 | 1795 | 17591 |
| 9 | 30 | 8,334 | 1490 | 14602 | 1780 | 17444 |
| 10 | 32 | 8,8896 | 1500 | 14700 | 1730 | 16954 |
| 11 | 34 | 9,4452 | 1490 | 14602 | 1705 | 16709 |
| 12 | 36 | 10,0008 | 1475 | 14455 | 1690 | 16562 |
| 13 | 40 | 11,112 | 1390 | 13622 | 1610 | 15778 |
| 14 | 44 | 12,2232 | 1295 | 12691 | 1540 | 15092 |
| 15 | 48 | 13,3344 | 1195 | 11711 | 1460 | 14308 |
| 16 | 52 | 14,4456 | 1090 | 10682 | 1380 | 13524 |
| 17 | 56 | 15,5568 | 1010 | 9898 | 1285 | 12593 |
| 18 | 60 | 16,668 | 1005 | 9849 | 1185 | 11613 |
| 19 | 65 | 18,057 | 1060 | 10388 | 1060 | 10388 |
| 20 | 70 | 19,446 | 1190 | 11662 | 960 | 9408 |
3. Первая модельная задача
Нахождение корня шаговым методом:
| V | F(V) |
| 37,5 | 400,5 |
| 37,75 | 275,77 |
| 38 | 151,04 |
| 38,25 | 26,31 |
| 38,5 | -98,42 |
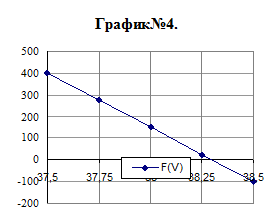
Уточнение корня методом Ньютона:
| e= | 0,001 | ||
| Метод Ньютона | |||
| V | F(V) | F'(V) | |F(V)<=e |
| 38,25 | 26,31 | -498,92 | |
| 38,302734 | 0 | -498,92 | скорость! |
Время разгона: метод Симпсона (парабол)
| V | F(V) | V | F(V) |
| 0 | 0,758765 | 7 | 0,9284421 |
| 4 | 0,8472437 | 15 | 1,2471831 |
| 12 | 1,1049336 | 25 | 2,184722 |
| 20 | 1,5878926 | 35 | 8,7996116 |
| 30 | 3,5003862 | 45 | -4,3394984 |
| 40 | -17,12329 | ||
| Sum1= | 7,0404562 | Sum2= | 8,8204604 |
| t _разгона = | 50,29 |
Время торможения: метод Симпсона (парабол)
| 38,5 | -0,754877 | 36 | -0,8072993 |
| 33,5 | -0,867546 | 31 | -0,9375089 |
| 28 | -1,037956 | 25,5 | -1,1397167 |
| 23 | -1,263599 | 20,5 | -1,4176964 |
| 18 | -1,614599 | 15,5 | -1,8750178 |
| 13 | -2,235598 | 10,5 | -2,7678834 |
| 8 | -3,632847 | 6 | -4,8437959 |
| 5 | -5,812555 | 4 | -7,2656939 |
| 3 | -9,687592 | 2 | -14,531388 |
| 1 | -29,06278 | 0,5 | -58,125551 |
| Sum1= | -55,21507 | Sum2= | -35,586 |
| t_торможения= | 73,75825 | ||
Энергия разгона судна:
| V(t) | V(t)^2 | ||
| 3,8 | 14,44 | ||
| 7,6 | 57,76 | ||
| 11,4 | 129,96 | ||
| 15,2 | 231,04 | ||
| 19 | 361 | ||
| 22,8 | 519,84 | ||
| 26,6 | 707,56 | ||
| 30,4 | 924,16 | ||
| 34,2 | 1169,64 | ||
| 38 | 1444 | ||
| E_разгона= | 40305650 | [Дж] | |
4. Вторая модельная задача
Нахождение корня шаговым методом:
| V | F(V) |
| 77 | 67 |
| 77,11 | 47,42 |
| 77,22 | 27,84 |
| 77,33 | 8,26 |
| 77,44 | -11,32 |
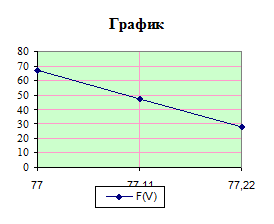
Уточнение корня:
| e= | 0,001 | ||
| Метод Ньютона | |||
| V | F(V) | F'(V) | |F(V)<=e |
| 77,33 | 8,26 | -178 | |
| 77,376404 | 0 | -178 | скорость! |
5. Третья модельная задача
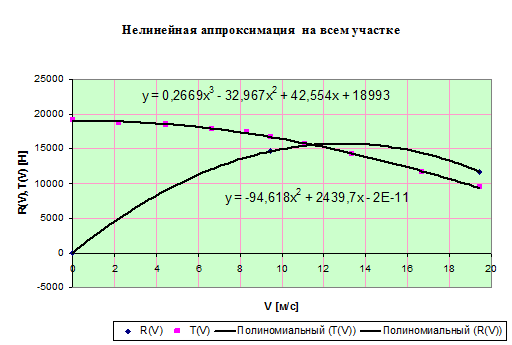
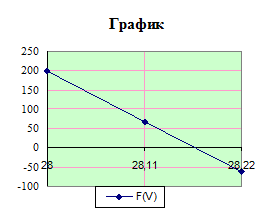
Нахождение корня:
| V | F(V) |
| 28 | 197,3728 |
| 28,11 | 67,90212 |
| 28,22 | -61,82168 |
| 28,33 | -191,7965 |
| 28,44 | -322,0201 |
6.Сводная таблица результатов и выводы
Таблица полученных результатов:
| Реализация | V ст | Разгон | Торможение | ||||
| T , c | S , м | E, МДж | T, c | S, м | |||
| Модельная задача №1 | MathCAD | 14,964 | 2,165 | 2,118 | 0,5 | 12,892 | 4,525 |
| Visual C++ | 15,33 | 2,16 | x | 0,14 | 3,56 | x | |
| Модельная задача №2 | MathCAD | 18,1 | 2,714 | 1,386 | 0,237 | 21,025 | 3,317 |
| Visual C++ | 18,25 | 1,64 | x | x | x | x | |
| Модельная задача №3 | MathCAD | 11,078 | 1,825 | -9,714 | 13,44 | 11,679 | -15,637 |
| Visual C++ | 11,31 | 1,87 | x | 18,28 | 3,63 | x | |
Вывод: результаты вычислений могут меняться в зависимости от метода и программы, которыми мы считаем. Причем некоторые методы не дадут нам вовсе правильного результата.