Реферат: Пересечение луча с поверхностью

Московский Авиационный Институт

Реферат

По дисциплине “Компьютерная графика”

На тему “Пересечение луча с поверхностью”

Выполнила: студентка группы 06-421, Трушина Ольга

2009г.

Введение.

Для начала изучим в общих чертах предметную область и определим, для чего нам требуется изучать пересечение луча с поверхностью.

Построение трёхмерного компьютерного изображение построена на методе трассировки лучей. При помощи этого метода моделируется физический процесс распространения световых лучей. Предполагается, что некоторый источник испускает лучи, лучи взаимодействуют с рассматриваемыми объектами и попадают в приёмник – человеческий глаз. Хотя на практике, видимых лучей – бесконечное множество, ограничиваются некоторым конечным их количеством, достаточным для изображения сцены. Сценой будем называть – совокупность объектов и окружающего их интерьера. Количество рассматриваемых лучей зависит от того, какого качества необходимо достигнуть. Основную цель метода трассировки лучей можно сформулировать, как необходимость определить освещённость каждой точки поверхности. Освещённость задаётся двумя основными составляющими – общей энергией света и энергией падающих лучей, которые уже отразились от других предметов сцены. Энергия падающего луча очень сильно зависит от свойств поверхности рассматриваемого предмета, а также, других предметов сцены. К определяющим свойствам поверхности относятся: прозрачность, цвет, шероховатость и отражающая способность.

Для каждого луча решается задача пересечения с объектами сцены. В зависимости от направления луча и расположения объектов, луч может либо уйти за пределы сцены, без взаимодействия с объектами, либо пересечь, некоторый встретившийся на пути предмет. При пересечение лучом поверхности предмета происходит следующее: часть энергии света поглощается материалом, а оставшаяся часть разделяется на две составляющие : отражённый и преломленный лучи. Эти лучи называют вторичными лучами. Процентное соотношение, в котором изначальна энергия луча распределится после взаимодействия с предметом вычисляется достаточно сложно и зависит от ряда факторов. Среди них: физико-механические и оптические свойства материала поверхности, ориентация поверхности в пространстве, спектральный состав луча, и другое.

Образовавшиеся вторичные лучи, в свою очередь, продолжают распространяться в пространстве, и снова могут либо уйти за пределы сцены, либо столкнуться с некоторым предметом, образовав уже третичные лучи. Процесс этот может быть если не бесконечным, то иметь множество этапов. Проиллюстрировать его можно в виде дерева, каждый узел которого имеет 2 ветки.

Понятно, что при каждом пересечение поверхности лучом интенсивность нового луча убывает. Поэтому, необходимо установить некоторые границы , доесть величину минимального рассматриваемого луча. Граница устанавливается из тех соображений, что лучи с малой величиной становятся просто нечувствительными для глаза, и изображать их нет смысла.

В дальнейшем будем рассматривать исключительно задачи геометрической оптики. Наибольшую сложность расчёта взаимного положения луча с произвольной поверхностью имеют задачи пересечения, отражения и преломления. Рассмотрим подробно задачу пересечения луча с поверхностью.

Условные обозначения, принятые для изложения дальнейшего материала.

q – точка пересечения луча с поверхностью

f – функция, которой заданна поверхность

t -аргумент функции f.

-параметрическая функция, которой заданна поверхность

V – вектор, направленной из начальной точки в точку пересечения луча и поверхности

ε – заданная точность вычислений

– некоторая точка троектории

Алгоритм для построения пересечение луча с поверхностью.

Принцип прямолинейности распространения света позволяет построить алгоритм пересечения луча с ограниченной поверхностью. Этот алгоритм является основным при рассмотрение пересечение луча с поверхностью, поэтому, стоит рассмотреть его детально.

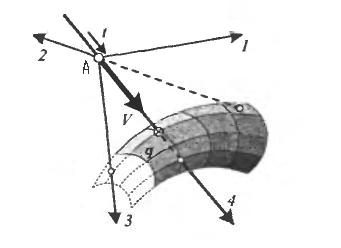
Алгоритм можно разделить на несколько шахов:

Шаг 1.

Расчитываем все точки пересечения луча с не ограниченной поверхностью,

, причём уравнение поверхности заданно формулой . Чтобы найти значения , необходимо решить уравнение , относительно t.

Если же поверхность определена параметрической функцией , то решается векторное уравнение , относительно трёх параметров t, ,.

Если уравненеие не имеет решений, это означает, что луч не пересекает поверхность. (Подобен лучу 1 на рисунке).

Шаг 2.

Список полученных точек сортируем по возрастанию значения . Причём, точки у которых <0 исключаем, как не принадлежащие лучу. Если после исключения таких точек список останется пустым, луч не пересекает поверхность. (Подобен лучу 2 на рисунке).

Шаг 3.

Ищим ближайший к началу списка элемент, для которого выполняется условие или принадлежности точки к ограниченной поверхности. Невыполнение условия означает, что луч (3) не пересекает поверхность внутри её границ. Найденный элемент является искомой точкой q, на луче (4).

Рассмотрим некоторые вычислительные аспекты пересечения прямой с поверхностью.

Точное аналитическое решение уравнения или возможно только для поверхностей первого или второго порядка. Для пересечения луча с более сложными поверхностями необходимо применять численные методы. Рассмотрим некоторые, наиболее часто используемые.

Для решения уравнения подойдёт практически любой численный метод решения нелинейных уравнений. Например, метод проб, метод касательных, метод секущих, метод интеграции и другие. Простейшим для программирования является метод проб. Он не требует нахождения производных и заключается в трассировки луча от начальной точки, в направление вектора V, с шагом . В точках троектории

Неявная функция поверхности имеет значения . Первый же найденный интервал на котором выполняется условие пропорционально дробится точкой

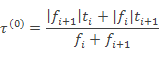
, на два интервала [] и []. Из них выбирается интервал [] с разнозначными кольцевыми значениями, для которых . Дехотомический процесс даёт последовательность значений {} и заканчивается при достижение желаемой точности ε по алгоритму || или (и) функции

||.

Как основные проблемы этого метода можно отметить:

· Сложность выбора шага- при слишком большом время расчёта будет слишком большим, а при слишком малом – недостаточное качество расчёта.

· Необходимость ограничения пространства распространения луча габаритами сцены.

Список используемой литературы:

1. Е. А. Никулин. Компьютерная геометрия и алгоритмы машинной графики.

2. Д. Роджерс. Алгоритмические основы машинной графики.