| Скачать .docx |
Реферат: Представление чисел в ЭВМ
Содержание
Задание 1. Перевод чисел из одной позиционной системы в другую……………………….…3
1.1 Перевод чисел из десятичной системы счисления в двоичную…………………....3
1.2 Изображение чисел в форме с фиксированной запятой (ФЗ).…….………………..5
1.3 Изображение чисел в форме с плавающей запятой (ПЗ)…………………..……….6
Задание 2. Сложение двоичных чисел…………………………………………………....….…..7
2.1 Сложение чисел в форме с ФЗ в обратном коде (ОК)………………………………7
2.2 Сложение чисел в форме с ФЗ в дополнительном коде (ДК)………………………8
2.3 Сложение чисел в форме с ФЗ в модифицированном коде………………...………8
2.4 Сложение чисел в форме с ПЗ………………………………………………….….…9
Задание 3. Умножение двоичных чисел………………………………………………………..11
3.1 Умножение чисел с ФЗ в ПК, используя первый способ умножения…………....11
3.2 Умножение чисел с ФЗ в ДК, используя второй способ умножения………….....13
3.3 Умножение чисел с ФЗ в ДК, используя третий способ умножения……...……...15
3.4 Умножение чисел с ПЗ, используя четвертый способ умножения……..……...…16
Задание 4. Деление двоичных чисел………………………………………………..…………..19
4.1 Деление чисел с ФЗ в ПК первым способом, применяя алгоритм с восстановлением остатков (ВО) и ОК при вычитании………………………………………………………………………………..……….19
4.2 Деление чисел с ФЗ в ПК вторым способом, применяя алгоритм без ВО и ДК
при вычитании………………………………………………………….…………….………….21
4.3 Деление чисел с ФЗ в ДК вторым способом, применяя алгоритм с автоматической коррекцией…………………………………………………………………………………..……23
4.4 Деление чисел с ПЗ первым способом…………………………………...…………24
Задание 5. Сложение двоично-десятичных чисел……………………………………………..27
5.1 Сложение двоично-десятичных чисел в коде 8-4-2-1………………………..……27
5.2 Сложение двоично-десятичных чисел в коде с избытком три………………..….28
5.3 Сложение двоично-десятичных чисел в коде 2-4-2-1………………………..……30
5.4 Сложение двоично-десятичных чисел в коде 3а+2………………………..………31
Задание 6. Умножение двоично-десятичных чисел…………………………………......…….32
6.1 Умножение старорусским методом удвоения – деления пополам……...………..32
6.2 Умножение методом десятично-двоичного разложения множителя………….....34
Список литературы………………………………………………………………………...…….36
I . Перевод чисел из одной позиционной системы счисления в другую с использованием промежуточных систем счисления и изображение чисел в форматах ЕС и СМ ЭВМ.
|
Любое число А в позиционной системе счисления (СС) с основанием q можно записать в виде:
A(q) = an
qn
+ an-1
qn-1
+…+ a1
q1
+ a0
q0
+ a-1
q-1
+…+ a-m
q-m
=![]() ,
,
где ak – цифра числа в данной СС;
qk – разрядный вес цифры ak ;
n+1 – количество разрядов в целой части числа;
m – количество разрядов в дробной части числа.
Чтобы перевести целое число в новую СС, его необходимо последовательно делить на основание новой СС до тех пор, пока не получится частное, у которого целая часть равна 0. Число в новой СС записывают из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа.
Чтобы перевести правильную дробь из одной позиционной СС в другую, надо её последовательно умножать на новое основание до тех пор пока в новой дроби не будет получено нужного количества цифр, определяемого заданной точностью. Правильная дробь в новой СС записывается из целых частей произведений, и старшей цифрой новой дроби будет целая часть первого произведения.
Формула для определения количества цифр в новой СС: 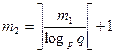 ,
,
где m1 – количество цифр исходной дроби с основанием p;
m2 – количество цифр в новой дроби с основанем q.
А=356,31
10сс – 8сс – 2сс
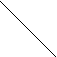
Перевод целой части:
|
![]()
![]()
![]() 356 8
356 8
![]()
![]() 4
44 8
4
44 8
![]() 4
5 8
4
5 8
5 0
Перевод дробной части :
Количество цифр после перевода дроби из 10 СС в 8 СС:
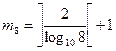 = 3
= 3
|
0 ,31
![]() 8
8
![]() 2
,48
2
,48
![]() 8
8
3, 84
![]() 8
8
6 ,72
Проверка:
2cc – 16сс – 10сс
0001 0110 0100 , 0100 1111 0000 2 = 164,4F16 = (1*256+6*16+4+4*16-1 +15*16-2 )10 =
1 6 4 4 15 0
= 356,3085…10 = 356,3110 (верный результат)
B =723,54
10сс – 16сс – 2сс
Перевод целой части:
|
![]()
![]()
![]() 723 16
723 16

![]()
![]() 3
45 16
3
45 16
![]() 13
2 16
13
2 16
2 0
Перевод дробной части:
Количество цифр после перевода дроби из 10 СС в 16 СС:
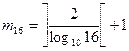 = 3
= 3
|
0 ,54
![]() 16
16
![]() 8
,64
8
,64
![]() 16
16
10 ,24
![]() 16
16
3 ,84
Проверка:
2cc – 8сс – 10сс
001 011 010 011 , 100 010 100 011 2 = 1323,42438 = (1*512+3*64+2*8+3+4*8-1 +2*8-2 +4*8-3 )10 =
1 3 2 3 4 2 4 3
= 723,539…10 = 723,5410 (верный результат)
|
Для двоичных чисел с ФЗ используют 3 формата фиксированной длины: полуслово – короткий с ФЗ (2 байта = 16 бит, 16 разрядов); слово – длинный с ФЗ (4 байта = 32 бита, 32 разряда); двойное слово – для промежуточных действий(8 байт = 64 бита, 64 разряда), чтобы обеспечить высокую точность вычислений. Двоичные операнды имеют вид целых чисел в дополнительном коде, у которых крайний левый разряд – знаковый. Это правило справедливо как для ЕС ЭВМ, так и для ПЭВМ.
А = 356,31
А = 101100100,0100111102 М=2-9
зн
![]()
![]()
|
B = -723,54
B = -1011010011,1000101000112 М=2-10
|
![]()
![]()
|
Двоичные числа с ПЗ изображаются по-разному в ЕС ЭВМ и ПЭВМ. Общим в изображении является лишь то, что порядки имеют смещения.
В ПЭВМ для чисел с ПЗ используются два формата: короткий и длинный. Смещенный порядок занимает восемь разрядов (смещение=128), крайний левый разряд сетки отводится под знак числа, остальные под мантиссу, изображенную в 2СС (23 разряда в коротком и 55 разрядов в длинном формате). Смещенный порядок содержит информацию о положении запятой в двоичной мантиссе числа. Для повышения точности представления мантиссы старший разряд ее, который в нормализованном виде всегда равен «1», может не заноситься в разрядную сетку, а просто подразумеваться.
В ЕС ЭВМ для чисел с ПЗ имеются три формата: короткий – слово, длинный - двойное слово и расширенный – учетверенное слово. Во всех этих форматах смещенный порядок занимает семь разрядов (смещение=64) и размещается в старшем байте вместе со знаковым разрядом числа. Остальные разряды (24 для короткого формата) занимает мантисса числа, изображаемая в 16 СС. Каждые 4 бита воспринимаются машиной как одна 16-ричная цифра, а в смещенном порядке содержится информация о положении запятой между 16-ричными, а не двоичными цифрами. Мантисса чисел с ПЗ всегда изображается в ПК и должна быть нормализована.
Сравнение представления мантисс с двоичным и шестнадцатеричным основанием показывает существенное расширение диапазона представления чисел в ЕСЭВМ.
А = -356,31
А = -000101100100,0100111102
р = 6
а) 2сс мантисса
зн 8 разрядов мантисса
![]()
![]()
![]() 1 1 0 0 0 1 0 0 1 1 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 1 1 0 0 0
1 1 0 0 0 1 0 0 1 1 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 1 1 0 0 0
б) 16сс мантисса
зн 7 разрядов мантисса
![]()
![]()
![]() 1 1 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0 0 1 0 0 1 1 1 1 0 0 0
1 1 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0 0 1 0 0 1 1 1 1 0 0 0
B = 723,54
B = 001011010011,1000101000112
р = 9
а) 2сс мантисса
зн 8 разрядов мантисса
![]()
![]()
![]() 0 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 0
0 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 0
б) 16сс мантисса
зн 7 разрядов мантисса
![]()
![]()
![]() 0 1 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1
0 1 0 0 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1
II . Сложение двоичных чисел.
Отрицательные числа в ЦВМ представлены в специальных кодах: прямом, обратном и дополнительном.
Прямой код (ПК) представляет абсолютное значение числа с закодированным знаком: « + » – «0», « - » – «1».
Обратный код (OK) положительного числа совпадает с его прямым кодом. Для отрицательного числа в знаковый разряд заносится «1», а в остальных разрядах цифры заменяются на взаимообратные (0 на 1, 1 на 0), т.е. формируется поразрядное дополнение числа до единицы.
Дополнительный код (ДК) положительного числа совпадает с его прямым кодом. Для отрицательного числа в знаковый разряд заносится «1», а в цифровой части числа цифры заменяются на взаимообратные и к полученному инверсному изображению прибавляется, единица в младший разряд, т.е. код является дополнением до основания СС.
Таким образом, положительные числа во всех кодах одинаковы, а отрицательные – различны.
|
При алгебраическом сложении чисел в ОК со знаковым разрядом оперируют как с разрядом цифровой части числа, а при возникновении единицы переноса из знакового разряда ее прибавляют к младшему разряду числа.
А =-356,3110 = -101100100,010011112
B = 723,5410 = 1011010011,1000101000112
Апк = 1, 01011001000100111100002
Впк = 0, 10110100111000101000112
Аок = 1, 10100110111011000011112
Вок = 0, 10110100111000101000112 М = 210
Сложение:
1, 1010011011101100001111
0, 1011010011100010100011
10, 0101 1 0 11 1 10 011101 1001 0
![]() 1
1
0, 0101101111001110110011
0, 0101101111001110110011ок = 101101111, 001110110011пк
101101111, 0011101100112 = 367,2310
Проверка:
(-356,31) 10 + 723,5410 = 367,2310
|
При алгебраическом сложении чисел в ДК результат получают также в ДК, а при возникновении единицы переноса из знакового разряда ее отбрасывают.
А=356,3110 = 101100100,010011112
B =-723,5410 = -1011010011,1000101000112
Апк = 0, 01011001000100111100002
Bпк = 1, 10110100111000101000112
Адк = 0, 01011001000100111100002
| |
М = 210
Сложение:
0, 0101100100010011110000
1, 0100101100011101011101
1, 1010010000110001001101
1, 1010010000110001001101дк = 1,0101101111001110110011пк
-101101111, 001110110011=-367,2310
Проверка:
356,3110 + (-723,54) 10 = -367,2310
|
Модифицированные обратный и дополнительный коды (МОК и МДК) имеют для изображения знака два соседних разряда: « + » – «00», « - » – «11». Эти коды используются для обнаружения ситуации ПРС - переполнения разрядной сетки. ПРС возникает при сложении чисел с ФЗ одинакового знака, когда результат операции выходит за верхнюю границу диапазона представления чисел, это приводит к потере старших разрядов.
Формальным признаком ПРС при использовании МОК и МДК является появление запрещенных комбинаций в знаковых разрядах – «01» или «10».
Для исправления результата можно либо увеличить масштаб результата, сдвинув его вправо на один разряд, а в освободившийся старший знаковый разряд поместить значение младшего знакового разряда, либо увеличить масштабы исходных операндов и выполнить арифметическую операцию снова.
А=-356,3110 = -101100100,010011112
B =-723,5410 = -1011010011,1000101000112
Апк = 1, 0101100100010011112
Bпк = 1, 10110100111000101000112
Амдк = 11, 1010011011101100012
Вмдк = 11,01001011000111010111012 М = 210
Сложение:
11,1010011011101100010000
11,0100101100011101011101
![]() 1 10
,1111001000001001101101
1 10
,1111001000001001101101
![]()
10 - запрещенная комбинация. Увеличиваем масштаб результата, сдвинув его вправо на один разряд, а в освободившийся старший знаковый разряд помещаем значение младшего знакового разряда:
1, 01111001000001001101101дк = -10000110111110110010011пк
-10000110111,1101100100112 = -1079,84810
Проверка:
-356,3110 + (-723,54)10 = -1079,8510
|
Сложение чисел в форме с ПЗ выполняется в несколько этапов. Числа с ПЗ изображаются двумя частями: мантиссой и порядком.
![]()
![]()
Чтобы их сложить, надо выполнить различные действия над мантиссами и порядками. Поэтому в машинах предусмотрены различные устройства для обработки мантисс и порядков. Мантиссы исходных операндов нормализованы.
1. Выравнивание порядков слагаемых: меньший порядок увеличивается до большего, при этом мантисса меньшего преобразуемого числа денормализуется. В машине выполняется вычитание порядков операндов. Знак и модуль разности порядков определяет, мантиссу какого из слагаемых надо сдвигать вправо и на сколько разрядов.
2. Сложение мантисс операндов по правилам сложения чисел с ФЗ.
3. Нормализация результата, если необходимо. При этом денормализация вправо, т.е. ситуация, когда в старшем разряде двоичной мантиссы «0», требует сдвига мантиссы влево и уменьшения порядка на соответствующее количество единиц. Денормализация влево означает временное ПРС мантиссы суммы, но в отличие от чисел с ФЗ, здесь возможна коррекция: сдвиг мантиссы на один разряд вправо и увеличение на «1» порядка суммы.
При больших величинах порядков возможно возникновении истинного ПРС числа с ПЗ, хотя вероятность этого невелика.
Смещенные порядки используются в большинстве современных ЭВМ для упрощения процесса выравнивания порядков и их сравнения.
При этом для представления порядка применяется специальный дополнительный код с инверсным кодированием знака: « + » – «1», « - » – «0». В результате порядки чисел увеличиваются (в ЕС ЭВМ на 26 =64, в СМ ЭВМ на 27 =128), что приводит к смещению всех порядков по числовой оси в положительном направлении. Такие смещенные порядки называют характеристиками, и так как они все оказываются целыми положительными числами, то алгебраическое сложение можно производить без предварительного анализа знаков.
А=356,31 = 101100100,010011112
B =723,54 = 1011010011,1000101000112
А
| 0 |
1 0 1 1 0 0 1 0 0 0 1 0 0 1 1 1 1 |
0 |
1 0 0 1 |
В
| 0 |
1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 |
0 |
1 0 1 0 |
Сложение:
1) Выравниваем порядки, для чего выполняем их вычитание с использованием ДК
РА = 0,1001
( Рв )дк = 1,0110
1,1111
(РА - РВ )дк =1,1111
(РА - РВ )пк =1,0001
РА - РВ = -1, значит денормализуем А – сдвигаем мантиссу на один разряд вправо и увеличиваем порядок А на 1.
А
| 0 |
0 1 0 1 1 0 0 1 0 0 0 1 0 0 1 1 1 1 |
0 |
01 0 1 0 |
2) Складываем мантиссы
0, 0101100100010011110000
0, 1011010011100010100011
1, 0000110111110110010011
![]()
ПРС! Сдвиг мантиссы на один разряд вправо и увеличение порядка суммы на 1.
0, 10000110111110110010011
А+В
| 0 |
1 0 0 0 0 1 1 0 1 1 1 1 1 0 1 1 0 0 1 0 0 1 1 |
0 |
1 0 1 1 |
Проверка:
10000110111, 1101100100112 = 1079,84710
356,31+723,54 = 1079,85
III . Умножение двоичных чисел.
Процесс умножения чисел в двоичной системе счисления прост, так как разрядами множителя могут быть либо «0», либо «1», и, следовательно, частичным произведением в каждом такте цикла умножения будет либо «0», либо множимое. Поэтому в цикле умножения двоичных чисел три элементарных операции:
1. анализ цифры очередного разряда множителя;
2. суммирование множимого с накопленной суммой частичных произведений, если цифра множителя «1»;
3. сдвиги в каждом такте умножения.
Умножение можно выполнять как с младших, так и со старших разрядов множителя, со сдвигом, как частичной суммы, так и множимого в процессе умножения. Этим объясняется существование четырех способов умножения чисел.
Следует обратить внимание на то, что множитель сдвигается во всех способах умножения, так как в каждом такте анализируется очередной разряд: при умножении с младших разрядов сдвиг вправо (в сторону младших разрядов), при умножении со старших разрядов множитель сдвигается влево. И еще одна особенность, позволяющая легко запомнить способы умножения: сумма частичных произведений обычно сдвигается в ту же сторону, что и множитель, а множимое сдвигается навстречу множителю, т.е. в противоположную сторону.
|
I способ - умножение с младших разрядов множителя со сдвигом суммы частичных произведений вправо.
Устройства, которые хранят операнды, регистры, имеют следующую разрядность:
1. регистры множителя и множимого – n-разрядные;
2. регистр частичных произведений – 2n-разрядный.
Суммирование множимого следует выполнять в старшие n разряды регистра суммы частичных произведений. Причем разрядность его можно уменьшить вдвое, до n разрядов, помещая при сдвиге младшие разряды суммы на место освобождающихся разрядов регистра множителя.
Особенность I способа умножения состоит в том, что имеется возможность временного переполнения разрядной сетки (ПРС) в регистре суммы частичных произведений, которое ликвидируется при очередном сдвиге вправо.
Алгоритм умножения двоичных чисел в прямом коде:
1. определить знак произведения путем сложения по модулю два знаковых разрядов сомножителей;
2. перемножить модули сомножителей одним из четырех способов;
3. присвоить полученному произведению знак из п.1. данного алгоритма.
C = 23 10
D = -57 10
С = 101112
D = -1110012
С пк = 0,010111 М = 26
D пк = 1,111001
D = 0,111001 – модуль множимого
![]() Знак произведения:
0 + 1 = 1
Знак произведения:
0 + 1 = 1
| Множитель
|
Сумма ЧП
|
Примечания |
| ,010111 |
0,000000 000000 |
|
| 0,111001 0,111001 000000 |
Сложение Сдвиг |
|
| ,001011 |
0,011100 100000 0,111001 1,010101 100000 |
Сложение Сдвиг |
| ,000101 |
0,101010 110000 0,111001 1,100011 110000 |
Сложение Сдвиг |
| ,000010 |
0,110001 111000 0,011000 111100 |
Сдвиг Сдвиг |
| ,000001 |
0,111001 1,010001 111100 |
Сложение Сдвиг |
| ,000000 |
0,101000 111110 0,010100 011111 |
Сдвиг |
Масштаб произведения: М = 212
Ответ:
1, 010100 011111пк = -101 000 1111 12 = 131110
Проверка:
2310 * (-57)10 = 131110
|
II способ - умножение с младших разрядов множителя со сдвигом множимого влево.
Устройства, которые хранят операнды, регистры, имеют следующую разрядность:
1. регистр множителя – n-разрядный;
2. регистры множимого и суммы частичных произведений – 2n-разрядный.
Первоначально множимое помещается в младшие разряды регистра, а затем в каждом такте сдвигается на один разряд влево.
Умножение чисел в дополнительном коде с автоматической коррекцией
Этот алгоритм разработан Бутом и является универсальным для умножения чисел в ДК. Сомножители участвуют в операции со знаковыми разрядами, которые рассматриваются как цифровые разряды числа. Результат получается сразу в дополнительном коде со знаком.
В процессе умножения анализируются две смежные цифры множителя: та, на которую выполняется умножение в данном такте – m1 , и соседняя младшая цифра – m2 . В двоичном множителе этой паре соответствуют четыре возможных набора – «00», «01», «10», «11», каждый из которых требует выполнения следующих действий:
1. набор «01» требует сложения множимого с предыдущей суммой частичных произведений;
2. набор «10» требует вычитания множимого из предыдущей суммы частичных произведений;
3. наборы «00» и «11» не требуют ни сложения, ни вычитания , так как частичное произведение равно нулю.
В цикле умножения в каждом такте выполняются соответствующие сдвиги на один разряд. При этом могут использоваться все четыре способа умножения с некоторыми особенностями:
1. в I способе не следует выполнять последний сдвиг суммы частичных произведений;
2. в IV способе не выполняется первый сдвиг множимого.
Это объясняется тем, что в этих тактах реализуется умножение не на цифровой, а на знаковый разряд числа.
Кроме того, при выполнении алгоритма умножения с автоматической коррекцией следует помнить о правилах сдвига отрицательных чисел в ДК : при сдвиге влево освобождающиеся младшие разряды заполняются нулями, при сдвиге вправо освобождающиеся старшие разряды заполняются единицами, т.е. реализуется арифметический сдвиг числа.
C = -2310 = -101112
D = 5710 = 1110012
C пк = 1,010111
D пк = 0,111001
С дк = 1,101001 М = 26
D дк = 0,111001 - множитель
|
|
|
Сумма ЧП |
Примечания |
| 0,1110010 0,0111001 |
1,111111 101001 1,111111 010010 |
0,000000 000000 0,000000 010111 0,000000 010111 |
Вычитание Сдвиги |
| 0,0011100 0,0001110 |
1,111110 100100 1,111101 001000 |
0,000000 010111 1,111111 010010 1,111111 101001 |
Сложение Сдвиги Сдвиги |
| 1,111111 101001 0,000010 111000 |
Вычитание |
||
| 0,0000111 |
1,111010 010000 |
0,000010 100001 |
Сдвиги |
| 0,0000011 0,0000001 |
1,110100 100000 1,101001 000000 |
Сдвиги Сдвиги |
|
| 0,000000 |
1,010010 000000 |
0,000010 100001 1,101001 000000 1,101011 100001 |
Сложение Сдвиги |
Ответ:
С*Dдк = -101011 1000012
С*Dпк = -010100 0111112
Проверка:
(-23)10 *5710 =(-1311)10
|
III способ - умножение со старших разрядов множителя со сдвигом суммы частичных произведений влево.
Устройства, которые хранят операнды, регистры, имеют следующую разрядность:
1. регистры множителя и множимого – n-разрядные;
2. регистр частичных произведений – 2n-разрядный.
Суммирование множимого следует выполнять в младшие n разрядов регистра суммы частичных произведений.
Особенность III способа умножения состоит в том, что в последнем такте не следует выполнять сдвиг в регистре сумм частичных произведений.
Алгоритм умножения двоичных чисел в ДК с простой коррекцией:
1. определить знак произведения путем сложения по модулю два знаковых разрядов сомножителей.
2. перемножить модули сомножителей, представленных в ДК, одним из четырех способов – получить псевдопроизведение.
3. если хотя бы один из сомножителей отрицателен, выполнить коррекцию по следующим правилам:
· если один сомножитель отрицателен, к псевдопроизведению прибавляется дополнительный код от модуля положительного сомножителя;
· если оба сомножителя отрицательны, к псевдопроизведению прибавляются дополнительные коды от модулей дополнительных кодов обоих сомножителей, т.е. их прямые коды.
4. Присвоить модулю произведения знак из п.1 данного алгоритма.
C = -2310 = -101112
D = -5710 = -1110012
C пк = 1,010111
D пк = 1,111001 М = 26
С дк = 1,101001
D дк = 1,000111
![]()
![]() С дк
= 0,101001 – модуль множимого
С дк
= 0,101001 – модуль множимого
![]()
![]() D дк
= 0,000111 – модуль множителя
D дк
= 0,000111 – модуль множителя
![]() Знак произведения:
1 + 1 = 0
Знак произведения:
1 + 1 = 0
| Множитель
|
Сумма ЧП
|
Примечания |
| ,0 00111 ,0 01110 ,0 11100 ,1 11000 |
,000000 000000 ,000000 000000 ,000000 000000 ,0000 0 0 101001 ,000000 101001 |
Сдвиг Сдвиг Сдвиг Сложение Сдвиг |
| ,1 10000 |
,000001 010010 ,000000 101001 ,000001 111011 |
Сложение Сдвиг |
| ,1 00000 |
,000011 110110 ,000000 101001 ,000100 011111 |
Сложение |
Псевдопроизведение = 0, 000100 011111
Коррекция (складываем модули операндов):
+0, 000100 011111
0, 010111
+0, 011011 011111
0, 111001
![]() 1, 010100 011111
1, 010100 011111
Ответ:
(C*D)пк =101000111112 = 131110
Проверка:
(-23)10* (-57)10 = 131110
|
IV способ - умножение со старших разрядов множителя со сдвигом множимого вправо.
Устройства, которые хранят операнды, регистры, имеют следующую разрядность:
1. регистр множителя – n-разрядный;
2. регистры множимого и частичных произведений – 2n-разрядный.
Первоначально множимое помещается в старшие разряды регистра, а затем в каждом такте сдвигается на один разряд вправо.
Особенность IV способа умножения состоит в том, что перед началом цикла умножения следует множимое сдвинуть на один разряд вправо.
Умножение чисел в форме с плавающей запятой
Когда сомножители заданы в форме с ПЗ, то их произведение определяется следующим образом:
![]()
Т.е. мантисса произведения mс равна произведению мантисс сомножителей, а порядок рс – сумме порядков сомножителей.
Это позволяет сформулировать алгоритм умножения чисел в форме с ПЗ:
1. определить знак произведения путем сложения по модулю два знаковых разрядов сомножителей;
2. перемножить модули мантисс сомножителей по правилам умножения дробных чисел с ФЗ;
3. определить порядок произведения алгебраическим сложением порядков сомножителей с использованием модифицированного дополнительного или обратного кодов;
4. нормализовать мантиссу результата и выполнить округление, если это необходимо.
Примечания:
1. Так как мантиссы исходных сомножителей нормализованы, то денормализация мантиссы произведения возможна только на один разряд.
2. При умножении чисел с ПЗ возможно возникновении ПРС при сложении порядков, поэтому необходимо предусматривать выявление признаков ПРС в устройствах умножения чисел с ПЗ.
C = -2310 = 101112
D = -5710 = 1110012
С
![]()
![]()
![]() зн мантисса порядок
зн мантисса порядок
![]() 0 1 0 1 1 1 0 0 00101
0 1 0 1 1 1 0 0 00101
D
![]()
![]()
![]()
![]() зн мантисса порядок
зн мантисса порядок
0 1 1 1 0 0 1 0 00110
![]() Знак произведения:
0 + 0 = 0
Знак произведения:
0 + 0 = 0
| Множитель n
|
|
Сумма ЧП 2n |
Примечания |
| 0,1 01110 0,0 11100 |
0,011100 100000 0,001110 010000 |
0,000000 000000 0,011100 100000 0,011100 100000 |
Сложение Сдвиги |
| 0,1 11000 |
0,000111 001000 |
Сдвиги |
|
| 0,011100 100000 0,000111 001000 0,100011 101000 |
Сложение |
||
| 0,1 10000 |
0,000011 100100 |
Сдвиги |
|
| 0,1 00000 |
0,000001 110010 |
0,100011 101000 0,000011 100100 0,100111 001100 |
Сложение Сдвиги |
| 0,100111 001100 0,00 0001 110010 0,101000 111110 |
Сложение |
||
| 0,0 00000 |
0,000000 111001 |
Сдвиги |
Порядок произведения:
00,0110
00,0101
00,1011 = 1110
Выполняем нормализацию :
0,101000 111110 ( М=212 ) = 0,010100011111 (М=212 )
![]() зн мантисса порядок
зн мантисса порядок
![]()
![]() 0 10100011111 1011
0 10100011111 1011
Ответ:
(C*D)пк =101000111112 = 131110
Проверка:
2310* 5710 = 131110
IV . Деление двоичных чисел
Процесс деления состоит из последовательности операций вычитания и сдвигов, при этом операция вычитания заменяется операцией сложения остатка с делителем, представленным в обратном или дополнительном кодах.
При делении чисел в прямом коде знак частного определяется сложением по модулю два знаковых разрядов делимого и делителя, и далее в процессе деления участвуют модули операндов.
Так как операция деления обратна умножению и начинается всегда со старших разрядов, то существуют два способа деления – обращенный III и IV способы умножения. Причем нередко для реализации умножения и деления целесообразно использовать одно и то же оборудование: регистр множимого - как регистр делителя, регистр множителя – как регистр частного, а регистр частных сумм – как регистр делимого, в который заносят остатки от деления.
|
Алгоритм деления с восстановлением остатков:
1. Определить знак частного сложением по модулю 2 знаковых разрядов делимого и делителя. Далее использовать модули операндов.
2. Вычесть из делимого делитель, путем сложения в ОК или ДК.
3. Проанализировать знак остатка после первого вычитания:
а) если остаток положительный, то произошло ПРС, операцию следует прекратить до смены масштабов операндов;
б) если остаток отрицательный, то в частное занести «0» (этот разряд по окончании деления станет знаковым разрядом частного) и восстановить остаток, прибавив к нему делитель.
4. Выполнить сдвиги: частного на один разряд влево и остатка на один разряд влево (I способ) или делителя на один разряд вправо (II способ).
5. В цикле формирования цифр частного вычитать из остатка делитель, прибавляя его в ОК или ДК.
6. Проанализировать знак полученного остатка:
а) если ![]() > 0, то в частное заносится «1»;
> 0, то в частное заносится «1»;
б) если ![]() <0, то в частное заносится «0».
<0, то в частное заносится «0».
7. Восстановить отрицательный остаток, сложив его с делителем.
8. Выполнить сдвиги, как указано в п.4.
9. Завершить цикл формированием (n+1)-го остатка для округления частного.
10. Выполнить округление результата и присвоить частному знак из п.1.
C = 2310 = 101112
D = -5710 = -1110012
Спк = 0,010111- делимое М = 26
Dпк = 1,111001
Dок = 1,000110 - делитель
|
|
Делимое (Остатки)
|
Примечания |
| 0,000000 |
0,010111 1,000110 1 ,011101 0,111001 10,010110 1 0,010111 |
Вычитание Остаток, < 0 Восст. Остатка Сдвиги |
| 0,000000 |
0,101110 1,000110 1 ,110100 0,111001 10,101101 1 0,101110 |
Вычитание Остаток, < 0 Восст. Остатка Сдвиги |
| 0,000001 |
1,011100 1,000110 10,100010 1 0 ,100011 1,000110 |
Вычитание Остаток > 0 Сдвиги |
| 0,000011
0,000110
0,001100
0,011001
0,011001(1) |
1,000110 1,000110 10,001100 1 0 ,001101 0,011010 0,011010 1,000110 1 ,100000 0,111001 10,011001 1 0,011010 0,110100 1,000110 1 ,111010 0,111001 10,110011 1 0,110100 1,101000 1,101000 1,000110 10,101111 1 0, 110000 1,100000 1,100000 1,000110 10,100110 1 0 ,100111 |
Вычитание Остаток > 0 Сдвиги Вычитание Остаток <0 Восст. Остатка Сдвиги Вычитание Остаток < 0 Восст. Остатка Сдвиги Вычитание Остаток > 0 Сдвиги Вычитание Остаток > 0 |
Округление:
0,011001
1
0,011010
(C/D)пк = 0,011010
C/D = 0,0110102 = 0,4062510
Точный результат: C/D = -23/-57 = - 0,40351
Абсолютная погрешность: - 0,40625 + 0,40351 = - 0,00274
Относительная погрешность: (-0,00274)/(-0,40351) = 0,0068 , т.е. 0,7%
|
Алгоритм деления без восстановления остатков:
1. Определить знак частного путем сложения по модулю два знаковых разрядов делителя и делимого. Далее использовать модули операндов.
2. Вычесть из делимого делитель путем сложения в ДК или ОК.
3. Проанализировать знак остатка после первого вычитания:
а) если положителен, то произошло ПРС, операцию следует прекратить для смены масштаба операндов;
б) если остаток отрицателен, то в частное занести «0» и продолжить операцию деления.
4. Выполнить сдвиги частного на один разряд влево и остатка на один разряд влево (I способ) или делителя на один разряд вправо (II способ).
5. Если до сдвига остаток был положителен, то вычесть из остатка делитель, если был отрицателен – прибавить к остатку делитель.
6. Если вновь полученный остаток положителен, то в очередной разряд частного занести «1», в противном случае - «0».
7. Выполнить пп.4-6 алгоритма (n+1) раз, причем последний сдвиг частного не выполнять, т.к. (n+1)-ый разряд формируется для округления.
8. Выполнить округление результата и присвоить частному знак из п.1.
C = -2310 = -10111 2 - делимое
D = -5710 = -111001 2 - делитель
Спк = 1,010111
Dпк = 1,111001
Сдк = 1,101001 М = 26
Dдк = 1,000111
1 ![]() 1 = 0
1 = 0
| Частное (Влево)
|
|
Делимое (остатки) |
Примечания |
| 0,000000 0,000000 0,000001 0,000011 0,000110 0,001100 0,011001 0,011001 (1 ) |
0,111001 000000 0,011100 100000 0,001110 010000 0,000111 001000 0,000011 100100 0,000001 110010 0,000000 111001 0,000000 011100 |
0,010111 000000 1,000111 000000 |
Вычитание Остаток < 0 Сдвиги Сложение Остаток < 0 Сдвиги Сложение Остаток > 0 Сдвиги Вычитание Остаток > 0 Сдвиги Вычитание Остаток < 0 Сдвиги Сложение Остаток < 0 Сдвиги Сложение Остаток > 0 Сдвиги Вычитание Остаток < 0 |
| 1 ,011110 000000 0,011100 100000 |
|||
| 1 ,111010 100000 0,001110 010000 |
|||
| 10,001000 110000 0 ,001000 110000 1,111000 111000 |
|||
| 10,000001 101000 0 ,000001 101000 1,111100 011100 |
|||
| 1 ,111110 000100 0,000001 110010 |
|||
| 1 ,111111 110110 0,000000 111001 10,000000 101111 0, 000000 101111 |
|||
| 1,111111 100100 10, 000000 010011 0, 000000 010011 |
Округление:
0,011001
1
0,011010
(C/D)пк = 0,011010
C/D = 0,011010(2) = 0,4062510
Точный результат: C/D = -23/-57 = - 0,40351
Абсолютная погрешность: - 0,40625 + 0,40351 = - 0,00274
Относительная погрешность: ( (-0,00274)/(-0,40351) )= 0,0068 , т.е. 0,7%
|
Алгоритм деления в дополнительном коде (с автоматической коррекцией).
Операнды участвуют в операции деления со знаковыми разрядами. Знак частного определяется в процессе деления.
- Если знаки делимого и делителя совпадают, то в частное заносится «0», в противном случае – «1». Этот разряд знаковый.
- Если знаки операндов совпадают, то делитель вычитается из делимого, в противном случае делитель прибавляется к делимому.
- Если знак первого остатка совпадает со знаком делимого, то произошло ПРС. Операцию деления прекратить. В противном случае деление продолжить.
- Выполнить сдвиги частного и остатка на один разряд влево (I способ) или делителя на один разряд вправо (II способ).
- Все последующие остатки формируются по правилу: если знаки делителя и остатка до сдвига совпадали, то делитель вычесть из остатка, в противном случае – делитель прибавить к остатку.
- Если знаки нового остатка и делителя совпадают, то в очередной разряд частного занести «1», в противном случае – «0».
- Выполнить пп.4-6 (n+1) раз, причем последний сдвиг частного не выполнять.
- Выполнить округление результата.
C = -2310 = -101112 - делитель
D = 5710 = 1110012 - делимое
Спк = 1,010111
Dпк = 0,111001
Сдк = 1,101001 М = 26
Dдк = 0,000111
1 ![]() 0 = 1
0 = 1
| Частное (Влево)
|
|
Делимое (остатки) |
Комментарий |
|
| 0,000001 |
1,101001 000000 |
0,111001 000000 1,101001 000000 |
Срав. Знаков Сложение ПРС! |
|
| 10 ,100010 000000 |
||||
| Увеличиваем порядок делимого до 7 |
||||
| 0,000001 |
1,101001 000000 |
0,011100 100000 1,101001 000000 1 0, 000101 100000 |
Срав. Знаков Сложение ПРС! |
|
| Увеличиваем порядок делимого до 8 |
||||
| 0,000001 0,000010 0,000101 0,001011 0,010110 0,101100 1,011000 1,011000 (0 ) |
1,101001 000000 1,110100 100000 1,111010 010000 1,111101 001000 1,111110 100100 1,111111 010010 1,111111 101001 1,111111 110100 |
0,001110 010000 1,101001 000000 |
Срав. Знаков Сложение Сдвиги Вычитание Сдвиги Сложение Сдвиги Вычитание Сдвиги Вычитание Сдвиги Сложение Сдвиги Сложение Сдвиги Сложение |
|
| 1 ,110111 010000 0,001011 100000 |
||||
| 10 ,000010 110000 1,111010 010000 |
||||
| 1 ,111101 000000 0,000010 111000 |
||||
| 1 ,111111 111000 0,000001 011100 |
||||
| 10 ,000001 010100 1,111111 010010 |
||||
| 10 ,000000 100110 1,111111 101001 |
||||
| 10 ,000000 001111 1,111111 110100 |
||||
| 10 ,000000 000011 |
||||
(D/C)дк = 1,011000
(D/C)пк = 1,101000
Порядок частного:
0,0111
1,1011
![]()
![]() 10,0010=0,0010 = 210
10,0010=0,0010 = 210
D/C = 10,10002 = 2,5 M = 22
Точный результат: 57/(-23) = -2,4783
Абсолютная погрешность: |- 2,5+ 2,4783| = 0,0217
Относительная погрешность: (0,0217)/(2,4783) = 0,0088 , т.е. 0,9%
|
Деление чисел в форме с плавающей запятой
Когда операнды заданы в форме с ПЗ, то их частное определяется следующим образом:
![]()
Т.е. мантисса частного mС есть частное мантисс делимого и делителя, а порядок рС – сумма порядков операндов.
Это позволяет сформулировать алгоритм деления чисел в форме с ПЗ:
- Определить знак частного путем сложения по модулю два знаковых разрядов операндов.
- Разделить модуль мантиссы делимого на модуль мантиссы делителя по правилам деления дробных чисел с ФЗ.
- Определить порядок частного вычитанием порядка делителя из порядка делимого, используя ОК или ДК.
- Нормализовать мантиссу результата и присвоить знак из п.1.
В отличие от деления чисел с ФЗ при выполнении п.2 алгоритма, получение положительного остатка при первом вычитании не означает ПРС. При обработке чисел с ПЗ такая ситуация требует денормализации мантиссы делимого сдвигом её на 1 разряд вправо с одновременным увеличением порядка делимого на «1».
Однако ситуация ПРС при делении чисел с ПЗ возможна при вычитании порядков операндов, если они были разных знаков.
C = 2310 = 101112 - делитель
D = 5710 = 1110012 - делимое
Операнды в разрядной сетке условной машины
C = 2310 = 1011102
D = 5710 = 1110012 – делимое
Cпк = 0,0101112 М = 26
| C |
0 |
101110 |
0 |
0101 |
| D |
0 |
111001 |
0 |
0110 |
Cдк = 1,101001
0 ![]() 0 = 0
0 = 0
| Частное
|
|
Комментарии |
| 0,000000 |
0,111001 1,101001 10 ,100001 |
Вычитание ПРС! |
| Увеличиваем порядок делимого до 7 |
||
| 0, 000000 |
0,011100 1,101001 10 , 000101 |
Вычитание ПРС! |
| Увеличиваем порядок делимого до 8 |
||
| 0,000000 0,000001 0,00001 0 0,000101 0,001010 0,01 0100 0,101000 0,101000( 1 ) |
0,001110 1,101001 1 ,110111 1,101110 |
Вычитание Остаток < 0 Сдвиги Сложение Остаток > 0 Сдвиги Вычитание Остаток < 0 Сдвиги Сложение Остаток > 0 Сдвиги Вычитание Остаток < 0 Сдвиги Сложение Остаток < 0 Сдвиги Сложение Остаток < 0 Сдвиги Сложение Остаток >0 |
| 0,010111 10,000101 1 0, 000110 0,001100 |
||
| 0,001100 1,101001 1 ,110101 1,101010 |
||
| 1,101010 0,010111 10,000001 1 0 ,000010 0,000100 |
||
| 0,000100 1,101001 1 ,101101 1,011010 |
||
| 1,011010 0,010111 1 ,110001 1,100010 |
||
| 1,100010 0 ,010111 1 ,111001 1,110010 |
||
| 1,110010 0,010111 10,001001 1 0 , 001010 |
||
Порядок частного
0,0111
1,1011
![]()
![]() 10,0010=0,0010 = 210
10,0010=0,0010 = 210
Округление мантиссы:
0,101000
1
0,101001
| 0 |
101001 |
0 |
0010 |
D/C = 10,10012 = 2,5625
Точный результат: 57/(-23) = -2,4783
Абсолютная погрешность: |- 2,5625+ 2,4783| = 0,0842
Относительная погрешность: (0,0842)/(2,4783) = 0,034 , т.е. 3,4%
V . Сложение двоично-десятичных чисел
|
\\\
Код с естественными весами 8-4-2-1 .
| 10СС |
ПК |
ОК |
| 0 |
0000 |
1001 |
| 1 |
0001 |
1000 |
| 2 |
0010 |
0111 |
| 3 |
0011 |
0110 |
| 4 |
0100 |
0101 |
| 5 |
0101 |
0100 |
| 6 |
0110 |
0011 |
| 7 |
0111 |
0010 |
| 8 |
1000 |
0001 |
| 9 |
1001 |
0000 |
Каждая десятичная цифра в этом коде образуется естественным замещением ее двоичным эквивалентом.
Алгоритм сложения в коде 8-4-2-1.
1. Проверить знаки слагаемых. Отрицательные слагаемые преобразовать в обратный код для чего инвертировать тетрады и прибавить потетрадно код 1010. Единица переноса между тетрадами отбрасывается.
2. Сложить двоично-десятичные числа по правилам двоичной арифметики.
3. Выполнить коррекцию результата, прибавив код 0110 к неправильным тетрадам (1010, 1011,1100, 1101, 1110, 1111), а также к тетрадам, в которых сформировались единицы переноса при сложении. Здесь единица переноса из тетрады в тетраду учитывается.
4. Проверить знак результата. Если он отрицателен, то преобразовать его в ПК для чего инвертировать все тетрады и прибавить потетрадно код 1010. Единица переноса отбрасывается.
А=-356,31
B=-723,54
А=-0,035631
B=-0,072354
М=104
A8-2-4 = 1,0000 0011 0101 0110 0011 0001
B8-2-4 = 1,0000 0111 0010 0011 0101 0100
Обратный код:
| A: |
1, |
1111 |
1100 |
1010 |
1001 |
1100 |
1110 |
- инверсия |
| 1010 |
1010 |
1010 |
1010 |
1010 |
1010 |
- коррекция |
||
| AОК = |
1, |
1001 |
0110 |
0100 |
0011 |
0110 |
1000 |
Результат в ОК |
| B: |
1, |
1111 |
1000 |
1101 |
1100 |
1010 |
1011 |
- инверсия |
| 1010 |
1010 |
1010 |
1010 |
1010 |
1010 |
- коррекция |
||
| BОК = |
1, |
1001 |
0010 |
0111 |
0110 |
0100 |
0101 |
Результат в ОК |
Сложение чисел:
| AОК = |
1, |
1001 |
0110 |
0100 |
0011 |
0110 |
1000 |
| BОК = |
1, |
1001 |
0010 |
0111 |
0110 |
0100 |
0101 |
| 1, |
0010 |
1000 |
1011 |
1001 |
1010 |
1101 |
|
| 1 |
|||||||
| 1, |
0010 |
1000 |
1011 |
1001 |
1010 |
1110 |
Коррекция:
| 1, |
0010 |
1000 |
1011 |
1001 |
1010 |
1110 |
|
| 0110 |
0110 |
0110 |
0110 |
0110 |
|||
| (A+B)ОК = |
1, |
1000 |
1001 |
0010 |
0000 |
0001 |
0100 |
Перевод числа в ПК:
| (A+B)П К = |
1, |
0111 |
0110 |
1101 |
1111 |
1110 |
1011 |
- инверсия |
| 1010 |
1010 |
1010 |
1010 |
1010 |
1010 |
- коррекция |
||
| 1, |
0001 |
0000 |
0111 |
1001 |
1000 |
0101 |
Результат в ПК |
(A+B)пк = 1, 0001 0000 0111 1001 1000 01018-2-4
С учетом масштаба: (A+B) = -1079,8510
Проверка: A+B =-356,3110 - 723,5410 =-1079,8510
|
Код с избытком 3
| 10СС |
ПК |
ОК |
| 0 |
0011 |
1100 |
| 1 |
0100 |
1011 |
| 2 |
0101 |
1010 |
| 3 |
0110 |
1001 |
| 4 |
0111 |
1000 |
| 5 |
1000 |
0111 |
| 6 |
1001 |
0110 |
| 7 |
1010 |
0101 |
| 8 |
1011 |
0100 |
| 9 |
1100 |
0011 |
ПК получается прибавлением избытка 3 к коду 8-4-2-1.
Алгоритм сложения в коде с избытком 3
1. Проверить знаки слагаемых. Отрицательные преобразовать в ОК путем инвертирования тетрад.
2. Сложить двоично-десятичные числа по правилам двоичной арифметики.
3. Выполнить коррекцию результата, прибавив код 1101 к тетрадам суммы, из которых не сформировалась единица переноса и прибавив код 0011 к тетрадам суммы из которых сформировалась единица переноса. Единицу переноса между тетрадами при коррекции отбрасывать.
4. Проверить знак результата. Отрицательный преобразовать в ПК, инвертируя тетрады.
А = 356,31
В = - 723,54
А/ = 0,35631 М=103
В/ = - 0,72354
А2-10 = 0,0110.1000.1001.0110.0100
В2-10 = 1,1010.0101.0110.1000.0111
Вок = 1,0101.1010.1001.0111.1000
Сложение:
| 0, 0,0110.1000.1001.0110.0100 |
|
| 1, 1,0101.1010.1001.0111.1000 |
|
| 1,1100.0011.0010.1101.1100 |
|
| 1101 0011 0011 1101 1101 |
коррекция |
| 1,1001.0110.0101.1010.1001 |
инвертируем тетрады т.к. результат отрицательный |
| 1,0110.1001.1010.0101.0110 |
(А+В)8-4-2-1+3 = 1, 0110.1001.1010.0101.0110
Результат с учетом масштаба М=103
(А+В)= - 367,2310
Проверка:
356,3110 +(-723,54)10 = - 367,2310
|
Код 2-4-2-1
| 10СС |
ПК |
ОК |
| 0 |
0000 |
1111 |
| 1 |
0001 |
1110 |
| 2 |
0010 |
1101 |
| 3 |
0011 |
1100 |
| 4 |
0100 |
1011 |
| 5 |
1011 |
0100 |
| 6 |
1100 |
0011 |
| 7 |
1101 |
0010 |
| 8 |
1110 |
0001 |
| 9 |
1111 |
0000 |
Алгоритм сложения в коде 2-4-2-1.
1. Проверить знаки слагаемых. Отрицательные преобразовать в ОК, инвертируя тетрады.
2. Сложить двоично-десятичные числа по правилам двоичной арифметики.
3. Выполнить коррекцию суммы:
если каждая из исходных тетрад меньше 5, то
- коррекция не нужна ,если суммарная тетрада также <5
- если суммарная тетрада ³ 5, то необходима коррекция кодом +6 (0110).
- если одна из исходных тетрад <5, а другая – ³5, то коррекции не требуется.
- если каждая из исходных тетрад ³5, то
- коррекция не нужна, если тетрада суммы ³5
- если тетрада суммы <5, то нужна коррекция кодом –6 (1010)
ИЛИ!
1. Корректируется тетрада суммы прибавлением кода 0110, если содержится 0 в 4-м разряде тетрад обоих слагаемых и комбинации 10 или 01 в 4-м и 3-м разрядах тетрады суммы и есть единица либо во 2-м, либо в 1-м разрядах тетрады суммы.
2. Корректируется тетрада суммы прибавлением кода 1010, если содержится 1 в 4-м разряде обоих слагаемых и комбинация 01 или 10 в 4-м и 3-м разрядах тетрады суммы и есть 0 либо во 2-м, либо в 1-м разрядах тетрады суммы.
! Единица переноса между тетрадами не учитывается.
Проверить знак результата. Если результат отрицателен, преобразовать его в ПК, инвертировав все тетрады.
А = - 356,31
В = 723,54
А/ = - 0,35631 М=103
В/ = 0,72354
А2-4-2-1 = 1,0011.1011.1100.0011.0001
Аок = 1,1100.0100.0011.1100.1110
В2-4-2-1 = 0,1101.0010.0011.1011.0100
Сложение:
| 1, 1100.0100.0011.1100.1110 0, 1101.0010.0011.1011.0100 |
|
| 10,1001.0110.0111.1000.0010 1 |
|
| 0,1001.0110.0111.1000.0011 1010.0110.0110.1010 |
коррекция |
| 0,0011.1100.1101.0010.0011 |
(А+В)2-4-2-1 = 0, 0011.1100.1101.0010.00112-4-2-1
Результат с учетом масштаба М=103
(А+В)=367,2310
Проверка:
-356,3110 +723,5410 =367,2310
|
А = - 356,31
В = - 723,54
А/ = - 0,035631 М=104
В/ = - 0,072354
А3а+2 = 1,00010.01011.10001.10100.01011.00101
Аок = 1,11101.10100.01110.01011.10100.11010
В3а+2 = 1,00010.10111.01000.01011.10001.01110
Вок = 1,11101.01000.10111.10100.01110.10001
Сложение:
| 1, 11101.10100.01110.01011.10100.11010 1, 11101.01000.10111.10100.01110.10001 |
|
| 11,11010.11101.00110.00000.00011.01011 1 |
|
| 1,11010.11101.00110.00000.00011.01100 |
|
| 00010.00010.00010 00010 |
коррекция |
| 0,11010.11101.01000.00010.00101 01110 |
инвертируем т.к. результат отрицательный |
| 1,00101.00010.10111.11101.11010.10001 |
(А+В)3а+2 = 1, 00101.00010.10111.11101.11010.10001
Результат с учетом масштаба М=104
(А+В)= - 1079,8510
Проверка:
-356,3110 +(-723,54) 10 = - 1079,8510
VI . Умножение двоично-десятичных чисел.
|
Алгоритм умножения заключается в удвоении на каждом шаге множимого, что равносильно сдвигу его на один разряд влево, и делению пополам множителя, что равносильно сдвигу его на один разряд вправо. Шаги повторяются, пока множитель не станет равным нулю.
При сдвиге двоично-десятичных чисел (код 8-4-2-1) на один разряд как влево так и вправо необходима коррекция. При сдвиге влево коррекция производится точно так же, как и при сложении, то есть при появлении неправильных тетрад или единицы переноса из тетрады осуществляется прибавление к данной тетраде корректирующего кода 0110. При сдвиге вправо корректирующий код образуется как разница между математическим результатом деления двоичной тетрады пополам (16/2=8) и фактическим (10/2=5), 8-5=310=0011. Эту разницу нужно вынести из тетрады, в которой образовалась единица переноса. Таким образом, корректирующий код будет 310=-00112=1101ДК.
А = 35610
В = 72310
А = 0011.0101.01108-2-4-1 - множитель
В= 0111.0010.00118-2-4-1 - множимое
|
|
|
Произведение |
|
| 0011.0101.0110 0001.1010.1011 11 01 1101 0001.0111.1000 0000.1011.1100 . 1101 .1101 0000.1000.1001 0000.0100.0100 0000.0010.0010 0000.0001.0001 0000.0000.1000 1101 0000.0000.0101 0000.0000.0010 0000.0000.0001 |
0000.0000.0000.0111.0010.0011 0000.0000.0000.1110.0100.0110 0110 0000.0000.0001.0100.0100.0110 0000.0000.0010.1000.1000.1100 0 110 0000.0000.0010.1000.1001.0010 0000.0000.0101.0001.0010.0100 0110 011 0 0000.0000.0101.0111.1000.0100 0000.0000.1010.1111.0000.1000 0110 0110 0110 0000.0001.0001.0101.0110.1000 0000.0010.0010.1010.1101.0000 0110 0110 0110 0000.0010.0011.0001.0011.0110 0000.0100.0110.0010.0110.1100 0 11 0 0000.0100.0110.0010.0111.0010 0000.1000.1100.0100.1110.0100 0110 0110. 0000.1001.0010.0101.0100.0100 0001.0010.0100.1010.1000.1000 0110 0110. 0001.1000.0101.0000.1000.1000 |
0000.0000.0000.0000.0000.0000 0000.0000.0000.0000.0000.0000 0000.0000.0010.1000.1001.0010 0000.0000.0010.1000.1001.0010 0000.0000.0010.1000.1001.0010 0000.0010.0011.0001.0011.0110 0000.0010.0101.1001.1100.1000 0110 0000.0010.0101.1010.0010.1000 0000.0010.0101.1010.0010.1000 0000.0 100 . 0110 .0 010 .0 111.0 0 1 0 0000.0110.1011.1100.1001.1010 0110 0110 0110 0000.0111.0010.0010.1010.0000 0000.0111.0010.0010.1010.0000 0001.1000.0101. 0000. 1000.1000 0001.1111.0111.0011.0010.1000 0110 0110 0010.0101.0111.0011.1000.1000 2 5 7 3 8 8 |
Сдвиг Корр Сдвиг Корр Слож Сдвиг Корр Сдвиг Корр Сдвиг Корр Слож Корр Сдвиг Корр Слож Корр Сдвиг Корр СдвигКорр Слож Корр |
А*B = 0010.0101.0111.0011.1000.10008-2-4-1 = 257.38810
Проверка:
35610 *72310 = 257 38810
|
Метод основан на преобразовании множителя в виде суммы произведений десятичных чисел на степень двойки. Множитель представляется в коде 8-4-2-1. Особенностью преобразованного множителя является то, что десятичное число состоит только из символов 0 и 1, а слагаемых в нём не более четырёх. Каждое из четырёх частичных произведений получают последовательно сдвигом множимого на требуемое количество десятичных разрядов (тетрад) с подсуммированием и коррекцией. Умножение же на степень двойки равносильно сдвигу влево на 1 разряд с введением коррекции.
А2-10 = 0011.0101.01108-2-4-1 -множимое
В2-10 = 0111.0010.00118-2-4-1 - множитель
Преобразование множителя:
![]()
![]() B2-10
= 0111. 0010.00118-2-4-1
= (0*23
+ 1*22
+ 1*21
+ 1*20
)*102
+ (0*23
+ 0*22
+ 1*21
+ 0*20
)*101
+ (0*23
+ 0*22
+ 1*21
+ 1*20
)*100
= (000)*23
+(100)*22
+(111)*21
+(101)*20
B2-10
= 0111. 0010.00118-2-4-1
= (0*23
+ 1*22
+ 1*21
+ 1*20
)*102
+ (0*23
+ 0*22
+ 1*21
+ 0*20
)*101
+ (0*23
+ 0*22
+ 1*21
+ 1*20
)*100
= (000)*23
+(100)*22
+(111)*21
+(101)*20
A2-10 =0011.0101.01108-2-4-1
| Множитель (преобраз.) |
|
Произведение |
|||
| 100*22 |
*100 |
0000.0011.0101.0110.0000.0000 |
|||
| *21 |
0000.0110.1010.1100.0000.0000 |
||||
| Корр. |
0110.0110 |
||||
| 0000.0111.0001.0010.0000.0000 |
|||||
| *22 |
0000.1110.0010.0100.0000.0000 |
||||
| корр |
0 1 10 |
||||
| 0 0 01 .010 0 . 0 010.0100.00 0 0.0000
|
0 0 01 .010 0 . 0 010.0100.00 0 0.0000
|
||||
| *1 *10 |
0000.0000.0000.0011.0101.0110 0011.0101.0110.0000 |
||||
| 0000.0000.0011.1000.1011.0110 |
|||||
| Корр |
011 0 |
|
|||
| 111*21 |
11= |
0000.0000.0011.1001.0001.0110 |
|||
| +100 |
0000. 00 11 . 0101 . 0110.0000.0000 |
||||
| Корр |
0000.0011.1000.1111.0001.0110 0110 |
||||
| 111= |
0000.0011.1001.0101.0001.0110 |
||||
| *21 |
0000.0111.0010.1010.0010.1100 |
||||
| корр |
0110 0110 0110 |
||||
| 0000.0111.1 00 1 . 0 0 00.0011.0010 |
0000.0111.1 00 1 . 0 0 00.0011.0010 |
||||
| 101 |
*100 *1 |
0000.0011.0101.0110.0000.0000 0000.0000. 0000 . 00 11 . 0101 . 0110 0000.0011.0101.1001.0101.0110 |
0000.0011.0101.1001.0101.0110 |
||
| Сложение коррекция |
0001.0100.0010.0100.0000.00000000.0111.1 00 1 . 0 0 00.0011.0010 0001.1011.1011.0100.0011.0010 0110 0110 |
||||
|
|
сложение |
0010.0010.0001.0100.0011.0010 0000.0011.0101.1001.0101.0110 0010.0101.0110.1101.1000.1000 |
|||
| коррекция |
0110 |
||||
| 0010.0101.0111.0011.1000.1000 2 5 7 3 8 8 |
|||||
A*B=0010.0101.0111.0011.1000.10008-2-4-1 = 257 38810
Проверка: A*B =35610 *72310 = 257 38810
Список используемой литературы
1.Фадеева Т.Р., Долженкова М.Л. Организация арифметических операций над двоичными числами. – Киров: Изд-во ВятГУ, 2001. – 40 с.
2. Конспекты лекций по дисциплине «Информатика».