Реферат: Типовые звенья в системах автоматического управления

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. Королева

Кафедра летательных аппаратов

Расчетно-графическая работа по курсу

"Теория управления в организационно-технических системах"

Выполнил студент гр. 1314

Фаюстов А.П.

Принял

Доцент Давыдов Е.И.

Самара 2007

Лабораторная работа №1

Тема: «Типовые звенья и их соединения. Динамические характеристики типовых звеньев и их соединений»

Цель:

- Изучить динамические характеристики типовых звеньев и их соединений, а также методы их расчета. Провести оценку устойчивости САУ.

1. Структурная схема автоматической системы с численными значениями коэффициентов представлена на рисунке 1:

K₁ =2 T₂ =0,26 k₄ =3 T₄ =0,1 k₅ =1,285 T₅ =0,346 k₃ =1 c₅ =0,6

Рисунок 1-Структурная схема САУ

2. Преобразуем исходную схему к одноконтурной и определим передаточную функцию разомкнутой и замкнутой системы:

Структурная схема преобразованной САУ представлена на рисунке 2.

Рисунок 2- Структурная схема преобразованной САУ

3. Характеристический полином замкнутой системы:

4. Определим устойчивость системы по критерию Гурвица:

Данная система является устойчивой по критерию Гурвица.

5. Определим устойчивость САУ по критерию Михайлова:

Характеристическое уравнение замкнутой системы имеет вид:

Сделаем замену и выделим вещественную и мнимые части:

В точках пересечения кривой Михайлова с осью ординат вещественная часть равна 0, то есть =0. В точках пересечения кривой с осью абсцисс мнимая часть равна 0, то есть =0.

Для того, чтобы система была устойчива необходимо и достаточно, чтобы корни уравнений чередовались между собой.

Решая, получим:

Таким образом, условие выполняется. Кривая Михайлова приведена на рисунке 3.

Кривая Михайлова начинается на вещественной положительной полуоси и проходит последовательно 3 квадранта и заканчивается в третьем квадранте. Следовательно, при данных параметрах исследуемая система устойчива.

6. График переходного процесса представлен на рисунке 3

Рисунок 3-График переходного процесса.

7. Вывод по проделанной работе:

Данная система является устойчивой по критерию Гурвица и Михайлова. Также это видно по графику переходного процесса, представленного на рисунке 3.

Лабораторная работа №2

Тема: «Динамические характеристики типовых звеньев и их соединений. Анализ устойчивости САУ».

Цель:

- Изучить динамические характеристики типовых звеньев и их соединений, а также методы их расчета.

- Изучить методы моделирования систем в SIAM.

K₁ =2 T₂ =0,26 k₄ =3 T₄ =0,1 k₅ =1,285 T₅ =0,346 k₃ =1 c₅ =0,6

Рисунок 1-Структурная схема САУ

2. Преобразование исходной САУ к одноконтурной:

Структурная схема преобразованной САУ представлена на рисунке 2.

Рисунок 2- Структурная схема преобразованной САУ

3. Определение устойчивости САУ

График переходного процесса заданной САУ представлен на рисунке 3, график ЛЧХ-на рисунке 4.

Рисунок 3-График переходного процесса заданной САУ.

Рисунок 4- ЛЧХ САУ с коэффициентом усиления к=2

Характеристическая кривая критерия Найквиста, соответствующая данному случаю, изображена на рисунке 6.

Рисунок 6- Характеристическая кривая критерия Найквиста

Увеличивая далее коэффициент усиления САУ, получаем, что график переходного процесса будет более колебательным, САУ становится менее устойчивой, однако остается устойчивой, что видно из рисунка 7.

Рисунок 7-График переходного процесса с коэффициентом усиления к=15

Для того, чтобы получить неустойчивую САУ изменим постоянную времени T1, приравняв ее к 0.009. Тогда получим график переходного процесса для неустойчивой САУ (рисунок 8) и соответствующий график ЛЧХ (рисунок 9).

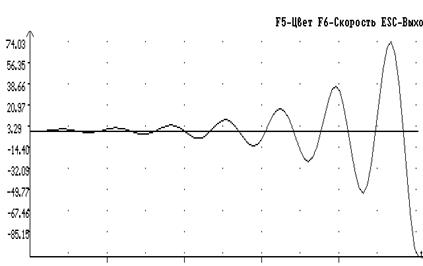
Рисунок 8-График переходного процесса САУ с коэффициентом усиления к=15.

Рисунок 9- ЛЧХ САУ с коэффициентом усиления к=15

Рисунок 10- Характеристическая кривая критерия Найквиста c k=15

Рисунок 11-График переходного процесса САУ с коэффициентом усиления к=.

4. Вывод по проделанной работе:

Данная система является устойчивой. Это видно по графику переходного процесса, показанного на рисунке 3. При увеличении коэффициента усиления система становится неустойчивой. Это видно из рисунков 8-10. На рисунках 8-10 график переходного процесса САУ с коэффициентом усиления к=15, где данная система неустойчива. На рисунке 11 график переходного процесса САУ с коэффициентом усиления к=, где данная САУ находится на границе устойчивости.

Лабораторная работа №3

Тема: «Качество процессов управления и коррекции САУ».

Цель: - ознакомиться с показателями качества переходного процесса.

- изучить методику коррекции САУ за счет:

- введения последовательного корректирующего устройства

- введения параллельного корректирующего устройства.

1. Структурная схема автоматических систем с численным значением коэффициента представлена на рисунке 1. График переходного процесса представлен на рисунке 2.

K₁ =2 T₂ =0,26 k₄ =3 T₄ =0,1 k₅ =1,285 T₅ =0,346 k₃ =1 c₅ =0,6

Рисунок 1- Структурная схема САУ

Рисунок 2- График переходного процесса

Качественные показатели:

сек,

2. Введем корректирующие устройства:

В схему на рисунке 1 введем последовательное корректирующее звено (рисунок 3) с параметрами:

Рисунок 3-Структурная схема скорректированной САУ.

График переходного процесса скорректированной САУ приведен на рисунке 4:

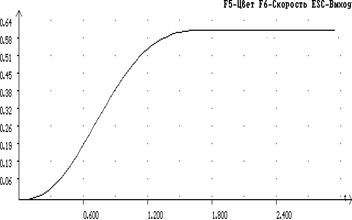
Рисунок 4- График переходного процесса скорректированной САУ.

В схему на рисунке 1 введем в обратной связи статическое звено с подобранным коэффициентом усиления (рисунок 5)

Рисунок 5-Структурная схема скорректированной САУ.

График переходного процесса скорректированной САУ зависит от коэффициента к обратной связи. Эти зависимости представлены на рисунках 6, 7, 8.

3. Выводы:

Введение последовательного корректирующего устройства:

Параметры корректирующего звена:

Введение параллельного корректирующего устройства:

При САУ устойчива. При дальнейшем увеличении коэффициента усиления САУ приходит в устойчивое состояние быстрее. При увеличении система становится неустойчивой.

Лабораторная работа №4

Тема: «Анализ нелинейной системы автоматического управления».

Цель:

¾ изучить методику исследования автоколебательных режимов методом фазовых траекторий;

¾ изучить методику моделирования нелинейной САУ в среде SIAM.

Содержание:

¾ экспериментальное определение предельных циклов нелинейной системы;

¾ оценка влияния начальных условий на устойчивость и качество переходных процессов.

Порядок выполнения работы:

1. Используя возможности вычислительной среды SIAM, набрать структурную схему на экране ПК в соответствии с рисунком 1.

Рисунок 1- Структурная схема заданной САУ

Исходные данные: K1=10, T1=1, K=5, T2=0,01, C=10

Начальное условие: X₄ (0)=1

Погрешность интегрирования по методу Фельдберга установить равной 0,001, конечное время интегрирования 20 c.

2. Построить фазовую траекторию, т.е. график выходного сигнала одного блока от выходного сигнала другого блока. Фазовую траекторию получить для двух значений начальных условий:

1. X₄ (0)=1 2. X₄ (0)=20

Фазовая траектория для схемы с идеальным двухпозиционным реле представлена на рисунках 2, 3.

Фазовая траектория для схемы с двухпозиционным реле с зоной нечувствительности представлена на рисунках 4, 5.

Рисунок 2- Фазовая траектория для схемы с идеальным двухпозиционным реле с начальными условиями X₄ (0)=1

Рисунок 3- Фазовая траектория для схемы с идеальным двухпозиционным реле с начальными условиями X₄ (0)=20

Рисунок 4- Фазовая траектория для схемы с двухпозиционным реле с зоной нечувствительности с начальными условиями X₄ (0)=1

Рисунок 5- Фазовая траектория для схемы с двухпозиционным реле с зоной нечувствительности с начальными условиями X₄ (0)=20