| Скачать .docx |
Курсовая работа: Современное состояние вычислительной техники
Ташкентский институт инженеров железнодорожного транспорта
Кафедра "Информатика и компьютерная графика"
«Информатика»
Выполнил:
студент группы ЕМ-477
Грачёв А.
Принял ассистент
Ташкент 2008
Введение
Современное состояние вычислительной техники
Типы оперативной памяти
Оперативная память (RAM, Random Access Memory, память произвольного доступа) - это энергозависимая среда, в которую загружаются и в которой находятся прикладные программы и данные в момент, пока вы с ними работаете. Когда вы заканчиваете работу, информация удаляется из оперативной памяти. Если необходимо обновление соответствующих дисковых данных, они перезаписываются. Это может происходить автоматически, но часто требует команды от пользователя. При выключении компьютера вся информация из оперативной памяти теряется.
В связи с этим трудно недооценить все значение оперативной памяти. Однако до недавнего времени эта область компьютерной индустрии практически не развивалась (по сравнению с другими направлениями). Взять хотя бы видео, аудиоподсистемы, производительность процессоров и. т. д. Усовершенствования были, но они не соответствовали темпам развития других компонентов и касались лишь таких параметров, как время выборки, был добавлен кэш непосредственно на модуль памяти, конвейерное исполнение запроса, изменен управляющий сигнал вывода данных, но технология производства оставалась прежней, исчерпавшей свой ресурс. Память становилась узким местом компьютера, а, как известно, быстродействие всей системы определяется быстродействием самого медленного ее элемента. И вот несколько лет назад волна технологического бума докатилась и до оперативной памяти. Быстрое усовершенствование оперативной памяти позволило кроме ее усовершенствования, значительно снизить цену на нее.
Но даже после падения цен, память системы, как правило, стоит вдвое дороже, чем системная плата. До обвального падения цен на память в середине 1996г. в течении многих лет цена одного мегабайта памяти держалась приблизительно на уровне 40 долларов. К концу 1996г. цена одного мегабайта памяти снизилась примерно до 4 долларов. Цены продолжали падать, и после главного обвального падения стоимость одного мегабайта не превышает доллара, или приблизительно 125 доларов за 128 Мбайт.
Хотя память значительно подешевела, модернизировать приходится ее намного чаще, чем несколько лет назад. В настоящее время новые типы памяти разрабатываются намного быстрее, и вероятность того, что в новые компьютеры нельзя будет устанавливать память нового типа, как никогда велика.
От количества установленной в компьютере оперативной памяти напрямую зависит возможность, какими программами вы сможете на нем работать. При недостаточном количестве оперативной памяти многие программы либо вовсе не будут работать, либо станут работать крайне медленно. Можно привести следующую приблизительную классифика-цию возможностей компьютера, в зависимости от объема оперативной памяти:
1 Мбайт и менее - на компьютере возможна работа только в среде DOS. Такие компьютеры можно использовать для корректировки текстов или ввода данных;
4 Мбайта - на компьютере возможна работа в среде DOS, Windows 3.1 и Windows for Workgroups. Работа в DOS вполне комфортна, а в Windows - нет: некоторые Windows-программы при таком объеме памяти не работают , а некоторые позволяют обрабатывать лишь небольшие и несложные документы. Одновременный запуск нескольких Windows-программ также может быть затруднен;
8 Мбайт - обеспечивается комфортная работа в среде Windows 3.1, Windows for Workgroups, при этом дальнейшее увеличение объема оперативной памяти уже практически не повышает быстродействие для большинства офисных приложений. Использование более новых операционных систем, как Windows 95 и OS/2 Warp, в принципе возможно, но работать они будут явно медленно; 16 Мбайт - обеспечивается комфортная работа в операционных системах Windows 95 и OS/2, причем дальнейшее увеличение объема оперативной памяти уже практически не повышает быстродействие при выполнении большинства офисных приложений. Возможно использование Windows NT, хотя ей не помешает добавить еще 8-16 Мбайт;
32 Мбайта и более - такой объем оперативной памяти может требоваться для серверов локальных сетей, компьютеров, используемых для обработки фотоизображений или видеофильмов, и в некоторых других приложениях. Полезен он может быть и для компьютеров, работающих под управлением ОС Windows NT.
Всю память с произвольным доступом (RAM) можно разделить на два типа:
1. DRAM (динамическая RAM)
2. SRAM (статическая RAM).
Причем независимо от типа оперативная память ЭВМ является адресной. Это значит, что каждой, хранимой в памяти единице информации ставится в соответствие специальное число, а именно адрес, определяющий место его хранения в памяти. В современных ЭВМ различных типов, как правило, минимальной адресуемой единицей информации является байт (8-ми разрядный код). Более крупные единицы информации - это слово и производные: двойное слово, полуслово и т. д. (образуется из целого числа байт). Обычно слово соответствует формату данных, наиболее часто встречающихся в данной машине в качестве операндов. Часто формат слова соответствует ширине выборке из основной памяти
Существуют несколько методов организации оперативной памяти:
1) Метод строк/колонок (Row/column) . При данном методе адресации ОП, последняя представляет собой матрицу разделенную на строки и колонки. При обращении к ОП одна часть адреса определяет строку, а другая - колонку матрицы. Ячейка матрицы, оказавшаяся на пересечении выбранных строки и колонки считывается в память или обновляется ее содержимое.
2) Метод статических колонок (Static-column) . При данном методе адресации ОП информация, относящаяся к какой-либо программе, размещается в определенной колонке. Последующее обращение к данной программе происходит в ту же самую колонку. За счет статичности части адреса (ее не надо передавать по адресной шине) доступ к данным осуществляется быстрее.
3) Метод чередования адресов (Interleaved) , который впервые стал применяться в 386 моделях АТ компьютерах. Данный метод предполагает считывание (или запись) информации не по одному, а сразу по нескольким адресам: i, i+1, i+2 и т.д. Количество одновременно опрашиваемых адресов, по которым происходит считывание информации, определяет кратность чередования адресов, что соответствует количеству блоков ОП. На практике обычно используется 2-х или 4-х кратное чередование адресов, т.е. ОП делится на 2 или 4 блока.Запись информации в блоки осуществляется независимо друг от друга. Информация по адресу i хранится в первом блоке, по адресу i+1 - во втором блоке и т.д. Считываемая с блоков информация далее переписывается в кэш-память для последующей переработки.
4) Метод страничной организации (Page-mode) . При данном методе организации память адресуется не по байтам, а по границам страниц. Размер страницы обычно равен 1 или 2 Кбайта. Данный метод предполагает наличие в системе кэш-памяти емкостью не менее 128 Кб куда предварительно считываются требуемые страницы ОП для последующей переработки МП или другим устройством. Обновленная информация периодически из кэш-памяти сбрасывается в ОП.
Последние два метода системной организации памяти предполагают обязательное наличие в системе сверх быстродействующей кэш-памяти для опережающего (read-ahaed) чтения в нее информации из ОП с последующей обработкой ее микропроцессором, что снижает время простоя последнего и повышает общую производительность системы.
1. Решение задач на языке TurboPascal.
Задачи на массивы данных
Массив – упорядоченный конечный набор однотипных данных.
У каждого элемента массива есть индекс (номер). Массив характеризуется именем, количеством измерений (может быть одномерным, двумерным и т.д.) и размером.
Например, набор чисел: 2, 4, 6, 8, 10 можно рассматривать как массив А(5), состоящий из элементов: а1 =2, а2 =4, а3 =6, а4 =8, а5 =10. Четвертый элемент (индекс равен 4) этого массива равен 8.
Тип массива обозначается зарезервированным словом ARRAY, после которого указывается диапазон изменения номеров элементов и (после слова OF) тип элементов массива.
Общий вид описания одномерного массива в разделе VAR:
V: ARRAY [N..M] OF T;
где V – имя массива; N и M – нижний и верхний индексы массива; Т – тип массива.
Например:
M1: array [5..100] ofreal; {массив М1 действительных чисел с номерами от 5 до 100};
I: array [-1..5] ofinteger; {I – массив целых чисел с номерами от –1 до 5};
Один и тот же массив можно описать различными способами. Например, массив А, состоящий из 50 элементов, можно описать следующими способами:
1 способ: VAR A: ARRAY [1..50] OF REAL;
2 способ: CONST N=50;
VAR A:=ARRAY [1..N] OF REAL;
3 способ: TYPE T=ARRAY [1..50] OF REAL;
VARA:T;
При третьем способе типу массива А дается имя T с помощью описания типа (после слова TYPE). Это описание типа помещается в программу перед совокупностью описания переменных (перед VAR).
В программе элементы массивов вводятся и выводятся в цикле, организованном с помощью оператора FOR.
Задача на двумерный массив
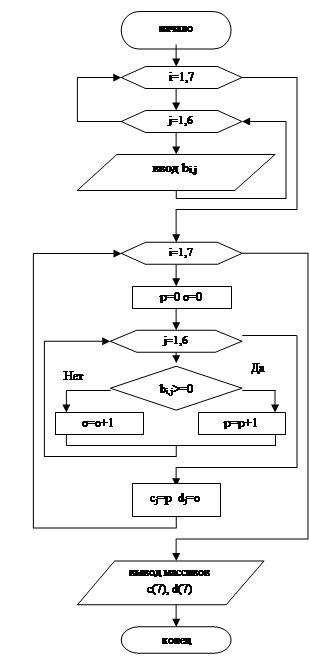
Определить количество положительных и отрицательных элементов каждой строки матрицы В(7,6) и записать результаты в новые массивы С и D.
program massiv;
var
i,j,p,o:integer;
b:array[1..7, 1..6] of integer;
c,d:array[1..7]of integer;
begin
writeln(‘Введите массив b(7,6)’);
for i:=1 to 7 do
for j:=1 to 6 do
readln(b[i,j]);
for i:=1 to 7 do
begin
p:=0; o:=0;
for j:=1 to 6 do
if b[i,j] >=0 then
p:=p+1 else o:=o+1;
c[j]:=p; d[j]:=o;
end;
for i:=1 to 7 do
writeln(‘c[‘,i,’]=’,c[i], ‘d[‘,i,’]=’,d[i]);
end.
ввод:
| 1 | -2 | 1 | -2 | 3 | 12 |
| 4 | 4 | 1 | 0 | -4 | -5 |
| 2 | -3 | 5 | 3 | 6 | 4 |
| 0 | -5 | 2 | 4 | 7 | -7 |
| -1 | 0 | -4 | 0 | 0 | -6 |
| 0 | 5 | 1 | 0 | -3 | 5 |
| 1 | 2 | -3 | -3 | -10 | 1 |
ответ:
c[1]=4 d[1]=2
c[2]=4 d[2]=2
c[3]=5 d[3]=1
c[4]=4 d[4]=2
c[5]=3 d[5]=3
c[6]=5 d[6]=1
c[7]=3 d[3]=3
1.2. Построение графика функции в алфавитно-цифровом или графическом режиме
Пусть нужно вывести на алфавитно-цифровой экран монитора график функции y= f(x) в заданном диапазоне изменения аргумента х от а до b с числом точек графика n (n£25). Перед выводом графика нужно напечатать вычисленные значения yi в виде таблицы, также напечатать наибольшее и наименьшее значения функции f(x).
Рассмотрим решение этой задачи на конкретном примере:
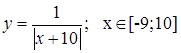 . Число точек графика равно 20.
. Число точек графика равно 20.
Примем ширину поля графика w, равной 61 позиции. Отступим от левого края экрана на m= 10 позиций. Для вывода строки графика выделим символьный массив С, состоящий из (w+m) элементов, т.е. 71 элемента. Масштаб по оси х примем равным шагу h при перемещении на одну строку. Масштаб по оси y выберем таким, чтобы максимально использовать поле графика w. Для это необходимо вычислить
ymax = max {yi } и ymin = min{yi }
i i
Определим масштаб my по формуле:
![]()
где ] [ - целая часть выражения; 0.5 добавлено для округления до ближайшего целого.
Масштаб my означает, что при каждом изменении значения функции на величину my символ, изображающий точку на графике, смещается в очередную позицию по строке.
По вычисленным значениям ymin и my определим номер позиции k, в которой изображается ось 0x :
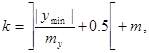
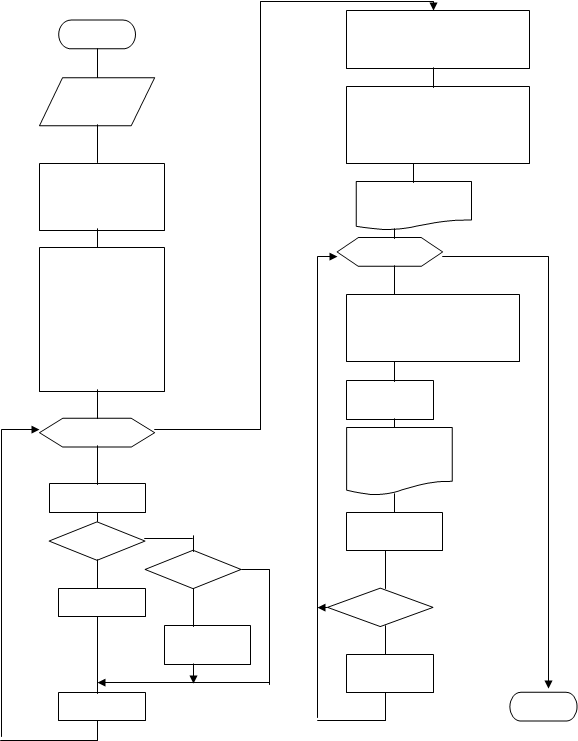
Для определения номера l позиции в строке, в которой надо изобразить значение yi , воспользуемся формулой
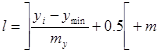 .
.
Для вывода собственно графика в цикле в очередной строке, соответствующей значениям аргумента xi и функции yi , выведем символ ‘I’ в позиции с номером k и символ ‘*’ в позиции с номером l ( при l = k в данной позиции следует выводить символ ‘*’).
Схема алгоритма решения задачи имеет вид:
Начало11
![]()
1 a, b, n
w, m 12
![]()
Ck =’I’
2 Заполнение
массива С 13 Заголовок
пробелами
14 i = 1, n
3
h = ![]()
ymax
=-105
15
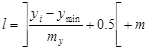
ymin =+105
x = a
16 Cl = `*`
4 i = 1, n 17 печать
массива C
5 yi = f(x)
6 yi > ymax нет 18 Cl = ` `
да8 yi < ymin нет
7 ymax =yi да нет 19 k = l
9 ymin = yi да
20 Cl = `I`
10 x = x + h конец
Пояснения . В блоке 2 символьный массив С заполняется пробелами. Блоки 3-10 организуют вычисление текущего значения функции yi = f(xi ), запоминание вычисленных значений yi в массиве y, состоящем из n элементов, вычисления наибольшего и наименьшего значений функции на заданном интервале изменения – аргумента x . В блоках 11-12 вычисляется масштаб my графика по оси y, номер k позиции в строке графика, соответствующий оси 0х , и осуществляется присваивание k-тому элементу массива c символа I.
Вычисление номера l в строке, соответствующей точке графика, занесение в l -й элемент массива c символа ‘*’ и печать символьного массива c реализуется блоками 15-17; восстановление символьного массива c в исходное состояние – блоками 18-20.
Программа, реализующая схему алгоритма, имеет вид:
PROGRAM GRAFIK;
CONST W = 61; M = 10;
VAR
Y: ARRAY [1..25] OF REAL;
C: ARRAY [1..71] OF CHAR;
K, L, N, I, J: INTEGER;
A, B, H, Y MAX, Y MIN, X, MY: REAL;
BEGIN
WRITELN (¢ВВЕДИТЕ A, B, N¢);
READ (A, B , N);
Y MAX = -1E4; YMIN:=+1E4;
H: = (B-A)/N;
![]() FOR I:=1 TO 71 DO C [ I ]: = ¢¢;
FOR I:=1 TO 71 DO C [ I ]: = ¢¢;
X: = A;
FOR I: = 1 TO N DO
BEGIN
Y[ I ]: = SIN(X)/X ;
IF Y [I ] > Y MAX THEN Y MAX: = Y [I ];
IF Y [I ] < Y MIN THEN Y MIN: = Y [I ];
X: = X+H;
END;
MY:=ROUND((YMAX-YMIN)/W+0.5);
K:=ROUND (ABS(YMIN)/MY+0.5)+M;
C[K]:= ¢I ¢ ;
WRITELN (¢ГРАФИКФУНКЦИИ Y=SIN(X)/X ¢);
WRITELN (¢ …………………………………¢);
FOR I:=1 TO N DO
BEGIN
L:=ROUND ((Y[ I ]- YMIN)/MY+0.5)+M;
C[ L]: = ¢ *¢;
FOR J: = 1 TO 71 DO
WRITE (C[J]);
![]() WRITELN (¢¢);
WRITELN (¢¢);
![]() C[ L]: = ¢¢;
C[ L]: = ¢¢;
 IF K =L THEN C [ L ]:= ¢I¢;
IF K =L THEN C [ L ]:= ¢I¢;
END;
END.
ввод:
a=0.1
b=2.5
n=40
2. Численные методы решения задач
2.1. Решение алгебраических и трансцендентных уравнений
К линейным уравнениям относятся алгебраические и трансцендентные уравнения. Уравнение называется алгебраическим, если функция f(x) представляет собой многочлен, какой-либо степени.
f(x)=a0 xm +a1 xm-1 +…+am-1 x+am =0
m![]() 3
3
Если же в функцию f(x) входят одновременно разные элементарные функции, то такое уравнение называется трансцендентным .
f(x)=sinx+lnx=0
Такие уравнения решаются приближенными методами. Решение разбивается на 2 этапа:
1). Отделение корней, т.е. нахождение достаточно малой области, содержащий один корень.
2). Уточнение корня заданной степенью точности.
Здесь известны следующие методы итераций, ньютона, хорды касательной половинного деления и т.д.
Отделение корней.
Пусть решается уравнение f ( x )= sinx + lnx =0 . Отделение корней можно сделать 2-мя способами:
графическим и алгебраическим.
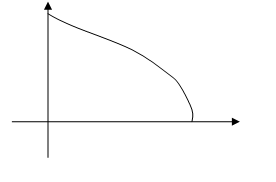
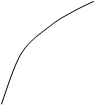
В графическом методе на координатной плоскости строится график функции и находится область пересечения функции с осью Х. В нашем случае удобно функцию разделить на 2 функции и на координатной плоскости построить оба графика, и найти область их пересечения.
sinx=-lnx
 f1
(x)=sinx
f1
(x)=sinx
 f2
(x)=-lnx
f2
(x)=-lnx
x [0;1]
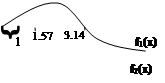 |
В алгебраическом методе отделения корней с некоторым шагом h просматривают достаточно большую область существования корня уравнений.
|
 |
|
|
|
|
|
|
|
|
Из математики известно, что непрерывная функция на небольшом отрезке содержит корень уравнения, если на концах отрезках функция f(x) имеет разные знаки.
Уточнение корня по методу половинного деления.
Пусть решается уравнение f(x)=0 и функция f(x) непрерывна на отрезке [a,b] =[x1 ,x2 ].
Отрезок [a,b] содержит корень, т.е. f(a)*f(b)<0.
Делим отрезок [a,b] пополам, т.е. выбираем начальное уравнение корня x=![]() , если f(x)=0, то х является корнем уравнения, если f(x) не равно нулю, то выбираем тот из отрезков [a,x] или [x,b], на концах которого функция f(x) имеет противоположные знаки. Выбранный отрезок снова делим пополам и проводим те же рассуждения. Процесс деления отрезков пополам продолжается до тех пор, пока длина отрезка на концах которого функция имеет разные знаки не станет < e
, если f(x)=0, то х является корнем уравнения, если f(x) не равно нулю, то выбираем тот из отрезков [a,x] или [x,b], на концах которого функция f(x) имеет противоположные знаки. Выбранный отрезок снова делим пополам и проводим те же рассуждения. Процесс деления отрезков пополам продолжается до тех пор, пока длина отрезка на концах которого функция имеет разные знаки не станет < e
[b-a]< e =10-5 .
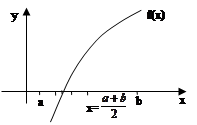 |
Схема реализации алгоритма имеет вид: [a,b]=[x1 ,x2 ] e=10-5
Уточнение корня по методу Хорд
По методу Хорд выбирается произвольное начальное значение корня из отрезка [a,b] на котором корень существует xÎ[a,b]=[x1 ,x2 ].
Затем по методу Хорд корень уточняется. Найденное новое значение корня подставляется в правую часть уравнения и т.д. пока разность между двумя приближениями не станет меньше ![]() <
e=
10-5
. Расчётная формула метода Хорд имеет вид:
<
e=
10-5
. Расчётная формула метода Хорд имеет вид:
xn
+1
=
xn
-
![]() (
b
-
x
).
(
b
-
x
).
Графический метод Хорд имеет вид:
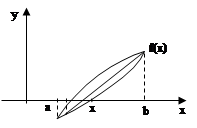 |
![]() Отделение корней
Отделение корней
 |
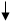 program otd;
program otd;
|
|
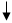 a,b,x1,x2,y1,y2,h,d:real;
a,b,x1,x2,y1,y2,h,d:real;
|


 begin
begin
|
|
|
 writeln(‘введите a,b,h’);
writeln(‘введите a,b,h’);
![]() readln(a,b,h);
readln(a,b,h);
|
y1:=f(x1);
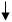 10: y2:=f(x2);
10: y2:=f(x2);
|
 if y1*y2<0 then writeln(x1:8:5,' ',x2:8:5);
if y1*y2<0 then writeln(x1:8:5,' ',x2:8:5);
 x1:=x2;x2:=x1+h;
x1:=x2;x2:=x1+h;
|
 if x2<=b then goto 10;
if x2<=b then goto 10;
readln;
end.
ввод:
0.1,10,1e-4
ответ:
х1=0.10000
х2=1.10000
Уточнение корней
![]()
![]()
![]() Метод половинного деления
Метод половинного деления
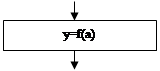 |
|
![]()
![]()
![]() label 2, 10;
label 2, 10;
|
|
 |
|
|
|
|



 f:= 2.2*x-exp(x*ln(2));
f:= 2.2*x-exp(x*ln(2));
|
|
|
![]()
![]() end;
end;
begin
|
![]()
|
![]() 10:x:=(a+b)/2;
10:x:=(a+b)/2;
![]()
![]() z:=f(x);
z:=f(x);
if z=0 then goto 2;
if y*z<0 then b:=x;
begin a:=x; y:=f(b); end;
if b-a>e then goto 10;
2:writeln('x=',x:8:5);
readln;
end.
ввод:
0.1, 1.1, 1е-5
ответ:
х=0.78111
М етод хорд

|
![]()
![]()
![]() label 10;
label 10;
|
|
![]() begin
begin
|
|
end;
|
![]() writeln(‘введите x,b,e’);
writeln(‘введите x,b,e’);
![]() readln(x,b,e);
readln(x,b,e);
![]() 10: y:=x-f(x)/(f(b)-f(x))*(b-x);
10: y:=x-f(x)/(f(b)-f(x))*(b-x);
![]() d:=abs(y-x);
d:=abs(y-x);
x:=y;
if d>e then goto 10;
y:=f(x);
writeln('x=',x:8:5);
end.
ввод:
0.1, 1.1, 1е-5
ответ:
х=0.78110
Проверка уравнения в ППП "Eureka"
Ввод:
2.2* x - exp ( x * ln (2))=0
Ответ:
X=0.78091254
Maximum error is 3.5465456e-7
2.2. Решение систем линейных уравнений методом итераций.
Метод итераций Гаусса-Зейделя
Метод последовательных приближений или итераций для больших n даёт сокращение времени решения на 20-30% по сравнению с точными методами.
В методе итераций число действий пропорционально числу n2 , тогда как в точных методах n3 .
Метод итераций особенно выгоден при решении систем, в которых много коэффициентов равно нулю. Рассмотрим метод на примере 3-х уравнений с тремя неизвестными.
Дана система:
|
Для сходимости метода итераций диагональные элементы системы должны быть преобладающие, т.е.
|aii |>>|aij |
Если это условие не выполняется, то делают элементарные преобразования системы.
Например:
|
|
Из 1-го уравнения преобразованной системы найдём х1 , из 2-го х2 из 3-го х3 . Получим:
|
Для удобства реализации алгоритма вычисляемое значение обозначим yi . Получим:
|
Для нашего примера система примет вид:
|
В качестве начального приближения для х1 ;x2 ;x3 , берётся 0 или 1. Подставляется в правую часть системы, получается новое значение xi , которое снова подставляется в правую часть и т.д. Пока разность между приближениями не станет меньше d).
![]() <=10-5
<=10-5
program lin;
var
b1,d,x1,x2,x3,x4,e,y1,y2,y3,y4:real;
begin
x1:=0; x2:=0; x3:=0; x4:=0; e:=1e-5;
repeat
y1:=(-9-x2+x4)/4;
y2:=(-y1+x3-3*x4)/2;
y3:=(-7-x1+3*y2)/4;
y4:=(2-3*x2+2*y3)/4;
d:=sqrt(sqr(x1-y1)+sqr(x2-y2)+sqr(x3-y3)+sqr(x4-y4));
x1:=y1; x2:=y2; x3:=y3; x4:=y4;
until d>E;
b1:=x1+2*x2-x3-3*x4;
writeln('x1= ',x1:8:5,' x2= ',x2:8:5,
![]()
![]() 'x3= ',x3:8:5,' x4= ',x4:8:5,' b1= ',b1:8:5);
'x3= ',x3:8:5,' x4= ',x4:8:5,' b1= ',b1:8:5);
|
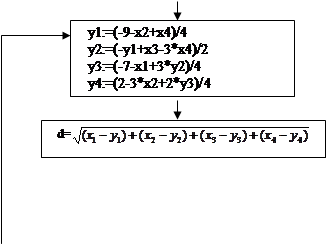 |
![]()
|
|
![]()
![]() x2= 4.00000
x2= 4.00000
|
![]() b1= 0.000000
b1= 0.000000
|
||
 |
||
Проверка в ППП "Eureka"
4*x1+x2-x4=-9
x1-3*x2+4*x3=-7
3*x2-2*x3+4*x4=12
x1+2*x2-x3-3*x4=0
Ответ:
Х1=-3.000000
Х2=4.000000
Х3=2.000000
X4=1.000000
2.3. Методы вычисления определённых интегралов
Если функция f(x) непрерывна на отрезке [a,b] и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница
![]() .
.
Как правило, выразить первообразную функцию удаётся не всегда, поэтому приходиться прибегать к приближённому интегрированию. Существует много численных методов: прямоугольников, трапеций, парабол или Симпсона и т.д.
Метод прямоугольников
Из математики известно, что интеграл равен площади криволинейной трапеции, ограниченной кривой f(x) осью Х и ординатами в точках а и b.
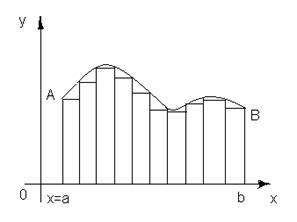
Для приближенного вычисления площади разобьём отрезок [а,b] на n части длинной h =( b - a )/ n .
В точках разбиения проведем ординаты до пересечения с кривой y=f(x), а концы ординат соединим прямоугольными отрезками, тогда площадь криволинейного приближенного прямоугольника можно считать равной площади фигуры ограниченной ломанной линией aABb. Площадь этой фигуры, которую обозначим через S, равна сумме площадей прямоугольников.
S = h ( y 0 + y 1 + y 2 +…+ yn )
Таким образом, приближенное значение интеграла по формуле прямоугольников запишется в виде
![]()
![]()
Точность метода с постоянным шагом h примерно e![]() h.
h.
Метод трапеции
В этом методе начальные построения те же, только при вычислении площади криволинейной трапеции ординаты сверху соединяются ломаной линией.
 |
Получается множество прямоугольных трапеций. Площадь одной трапеции равна:
S
тр
=
![]() .
h
.
h
Отсюда: y![]()
![]() .
h +
.
h + ![]() .
h + … +
.
h + … +![]() .
h =
.
h =
= h.
![]()
![]() +
f(a + h) +…+ f(в-h)
+
f(a + h) +…+ f(в-h)![]() =
=![]()
![]()
![]() +
+![]()
Точность Е
![]() h
2
h
2
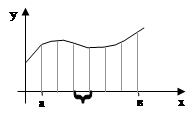
Метод Симпсона (парабол)
В этом методе отрезок [a,в] разбивается на 2n
частей, длинной h=![]() и ординаты сверху соединяются кривой второго порядка (3 соседних точки).
и ординаты сверху соединяются кривой второго порядка (3 соседних точки).
 |
||
|
||
Расчетная формула имеет вид :
у![]()
![]() (y0
+ 4y1
+ 2y2
+ 4y3
+ …+ 4y2n*1
+ y2n
)
(y0
+ 4y1
+ 2y2
+ 4y3
+ …+ 4y2n*1
+ y2n
)
y0 = f(a), y1 = f(a+2h), y2 = f(a+2h)… y2n-1 = f(в-h)
y2 n = f(в).
|
ci
=![]() , тогда формула примет вид:
, тогда формула примет вид:
у![]()
![]() (f(a)+f(в)+
(f(a)+f(в)+![]() (3+ci
))
(3+ci
))
![]()
![]() PROGRAM PRYAMOUGOLNIK;
PROGRAM PRYAMOUGOLNIK;
![]() CONST a= 0.4 ; b= 1.2; n=100;
CONST a= 0.4 ; b= 1.2; n=100;
![]()
![]() var x,y:real;
var x,y:real;
|
![]()
![]() function f (x:real):real;
function f (x:real):real;
![]()
![]()
![]()
![]() begin
begin
|
![]() end;
end;
|
![]()
![]() y:=0; x:=a;
y:=0; x:=a;
|
![]() begin
begin
![]() y:=y+f(x);
y:=y+f(x);
![]()
![]() x:=x+(b-a)/n;
x:=x+(b-a)/n;
end;
y:=y*(b-a)/n;
writeln('y=',y:8:5);
readln;
end.
ОТВЕТ:
y=0.28099
![]()

![]()
|
|
![]() var x,y,h,s:real;
var x,y,h,s:real;
![]()
|
 function f (x:real):real;
function f (x:real):real;
![]()
![]()
![]()
![]() begin
begin
|
![]() end;
end;
|
![]()
![]() h:=(b-a)/n;
h:=(b-a)/n;
|
![]() s:=(f(a)+f(b))/2;
s:=(f(a)+f(b))/2;
![]() while x<=b-h do
while x<=b-h do
![]() begin
begin
![]() s:=s+f(x);
s:=s+f(x);
x:=x+h;
end;
y:=s*h;
writeln('y=',y:8:5);
readln;
end.
ОТВЕТ:
y=0.28173
![]()
 |
||
![]()
|
|
![]() CONST a= 0.4; b=0.8; n=100;
CONST a= 0.4; b=0.8; n=100;
|
![]()
![]()
![]() c,n: integer;
c,n: integer;
|
![]() begin
begin
|
|
![]() begin
begin
 h:=(b-a)/(2*n);
h:=(b-a)/(2*n);
![]() s:=f(a)+f(b);
s:=f(a)+f(b);
|
![]() x:=a+h;
x:=a+h;
![]() 10: s:=s+(3+c)*f(x);
10: s:=s+(3+c)*f(x);
![]()
![]() x:=x+h;
x:=x+h;
c:=-c;
if x<= b-h then goto 10;
y:=s*h/3;
writeln('y=',y:8:5);
readln;
end.
ОТВЕТ:
y= 0.27919
Решение интеграла в ППП "Eureka"
y=integ((sin(x^2+0.5)/cos(x^2+0.5))/(1+2*x^2),x,0.4,0.8)
y=0.2823564
2.4 Методы решения дифференциальных уравнений
При использовании различных протекающих во времени процессах первым этапом является составление дифференциального уравнения, описывающего процесс, а вторым – поиск решения этого уравнения. Дифференциальным уравнением называется равенство, связывающее значение аргумента, неизвестной функции некоторых ее производных. Наивысший порядок входящих в уравнение производных называется порядком дифференциального уравнения.
Рассмотрим уравнение вида:
y=f(x,y) (1)
Уравннение (1) имеет бесконечное множество решений (рис. 1) – через каждую точку плоскости проходит интегральная кривая. Чтобы выделить одну кривую, нужно указать точку плоскости, через которую проходит кривая, т.е. указать так называемые начальные уравнения (значения x=x0 и y=y0 ) (2)

Метод Эйлера
Одним из методов решения дифференциального уравнения (1) с начальным условием (2) является метод Эйлера.
Будем рассматривать уравнение (1) на некотором отрезке [a,b]. Пусть отрезок поделен на n частей с шагом ![]() .
.
Обозначим X0 =a, X1 =X0 +h, X2 =X0 +2h,…, Xn =X0 +nh=b. Обозначим искомые y(X1 ),…y(Xn ) через y1 …yn .
Методика решения уравнения (1) с начальными условиями (2) связяна с разложением решения в ряд Тейлора в h-окрестности точки X0 .
![]()
При отбрасывании членов ряда, содержащие производные второго и высшего порядков, получим
![]()
где f(X,y) – правая часть уравнения (1).
Таким образом,
![]()
![]()
.
![]()
При достаточно малой величине шага h метод Эйлера дает решения с большей точностью, т.к. погрешность близка к h2 (h<<1) на каждом шаге интегрирования.
Метод Рунге-Кутта
Недостатком метода Эйлера является змедление вычислений при выборе малой величины шага h, задающей точность решения.
Наиболее распространенным методом численного интегрирования дифференциальных уравнений служит метод Рунге-Кутта, обеспечивающий ускорение за счет большей точности вычислений на каждом шаге. Точность метода Рунге-Кутта оценивается величиной E≈h2 .
Уточнение достигается за счет специального подбора координат четурех точек, в которых вычисляется первая производная f(x,y). Вместо первой производной h∙f(x,y) используемой в формуле Эйлера, вычисляется усредненная первая производная fi .
Формулы интегрирования по методу Рунге-Кутта имеют вид:
![]()
где ![]()
![]()
![]()
![]()
![]()
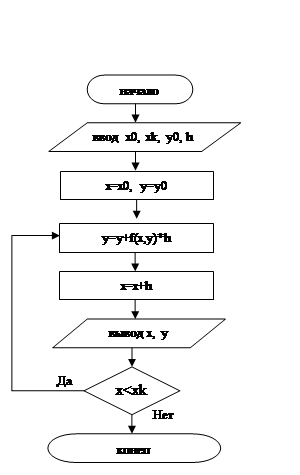 h=(xn
– x0
)/n i=0,1,2,…n
h=(xn
– x0
)/n i=0,1,2,…n
y’=(1-y2 )cos(x)+0.6y
при х0 =0; xn =1; у0=0; h=0.1
program eyler;
label 100;
const h=0.1; x0=0; xk=1; у0=0;
х0=а;
var h,y,x:real;
i: integer;
function f (x,y: real): real;
begin
f:= (1-y*y)*cos(x)+0.6*y;
end;
begin
y:=y0; x:=x0;
100: y:=y+h*f(x,y);
x:=x+h;
writeln(‘ x=',x:5:1,' y=',y:8:5);
if x<xk then goto 100;
readln;
end.
ответ:
x=0.1 y=0.1000
x=0.2 y=0.2045
x=0.3 y=0.3107
x=0.4 y=0.4156
x=0.5 y=0.5168
x=0.6 y=0.6121
x=0.7 y=0.7004
x=0.8 y=0.7814
x=0.9 y=0.8554
x=1.0 y=0.9234
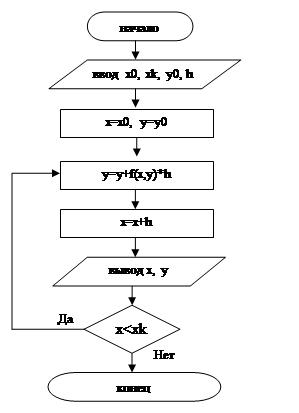 y’=(1-y2
)cos(x)+0.6y
y’=(1-y2
)cos(x)+0.6y
при х0 =0; xn =1; у0=0; h=0.1
program rungekutta;
label 100;
var
x,p,x0,y0,xk,y,a,b,c,d,h:real;
function f(x,y:real):real;
begin
f:= (1-y*y)*cos(x)+0.6*y;
end;
begin
x0:= 0; xk:=1; y0:= 0; h:=0.1;
x:=x0;y:=y0;
100: a:=h*f(x,y);
b:=h*f(x+h/2,y+a/2);
c:=h*f(x+h/2,y+b/2);
d:=h*f(x+h,y+c);
p:=(a+2*b+2*c+d)/6;
y:=y+p;
writeln('x=',x:8:1,'y=',y:8:5);
if x<xk then goto 100;
readln;
end.
ответ:
x=0.1 y=0.1025
x=0.2 y=0.2082
x=0.3 y=0.3141
x=0.4 y=0.4173
x=0.5 y=0.5156
x=0.6 y=0.6076
x=0.7 y=0.6926
x=0.8 y=0.7705
x=0.9 y=0.8419
x=1.0 y=0.9081
3. Оптимизационные модели
3.1. Решение транспортной задачи
Транспортная задача является частным случаем общей задачи линейного программирования. В линейном программировании функция цели и система ограничений заданна линейно.
Транспортная задача может быть решена основным методом линейного программирования – симплекс метода , но для неё разработаны более удобные и эффективные методы, в частности метод потенциала . Алгоритм транспортной задачи был впервые применён для рационализации перевозов груза, поэтому получил название транспортная задача .
Постановка задачи
Имеется m отправителей и n потребителей однородного груза. Запасы грухов у отправителей – ai , потребность в грузе у получателей – bj . Известна стоимость Сij перевозки единицы от каждого отправителя до каждого получателя. Требуется определить оптимальную схему перевозки груза от отправителей к получателям так, чиобы суммарные транспортные расходы были min. Обычно условие задачи записывается в виде таблицы:
| В1 | В2 | Вn | Запасы ai |
|
| А1 | С11 X11 |
С12 X12 |
С1n X1n |
a1 |
| А2 | С2 1 X21 |
С22 X22 |
С2n X2n |
a2 |
| Аm | Сm1 Xm1 |
Сm2 Xm2 |
Сmn Xmn |
am |
Потребность bj |
b1 | b2 | bn | S ai = S bj |
xij – количество груза, перевозимого от ai отправителя к bj потребителю.
При решении транспортной задачи должны выполняться 4 условия:
1. Все запасы грузов должны быть вывезены, т.е. ![]() i=1…
m
i=1…
m
2. Все потребности в грузе должны быть удовлетворены, т.е. ![]() j=1…
n.
j=1…
n.
3. Суммарные транспортные затарты должны быть min , т.е.
F=C11 ∙X11 + C12 ∙X12 +…+ Cmn ∙Xmn ® min
или ![]()
Существуют следующие методы решения задач:
1 Метод приближением условно оптимальными планами.
2 Метод потенциалов.
3 Метод рент.
4 Метод Филкерсона и т.д.
Расстановка поставок методом двойного предпочтения
1 итерация
| В1 | В2 | В3 | B4 | Uj | ||
| А1 | 5 |
4 |
2 45 |
2 45 |
90 | 0 |
| А2 | 3 80 |
6 |
3 |
1 15 |
95 | -1 |
| А3 | 1 10 |
2 90 |
3 |
7 |
100 | -3 |
| Фикт. | 0 |
0 -3 |
0 135 |
0 |
135 | -2 |
| 90 | 90 | 180 | 60 | |||
| Vi | 4 | 5 | 2 | 2 |
Fmin =90+90+240+15+10+180=625
2 итерация
| В1 | В2 | В3 | B4 | Uj | ||
| А1 | 5 |
4 |
2 90 |
2 |
90 | 0 |
| А2 | 3 35 |
6 |
3 -1 |
1 60 |
95 | 2 |
| А3 | 1 55 |
2 45 |
3 |
7 |
100 | 0 |
| Фикт. | 0 |
0 45 |
0 90 |
0 |
135 | -2 |
| 90 | 90 | 180 | 60 | |||
| Vi | 1 | 2 | 2 | -1 |
Fmin =180+105+60+55+90=490
Конечная таблица
| В1 | В2 | В3 | B4 | Uj | ||
| А1 | 5 |
4 |
2 90 |
2 |
90 | 0 |
| А2 | 3 |
6 |
3 35 |
1 60 |
95 | 1 |
| А3 | 1 90 |
2 10 |
3 |
7 |
100 | 0 |
| Фикт. | 0 |
0 80 |
0 55 |
0 |
135 | -2 |
| 90 | 90 | 180 | 60 | |||
| Vi | 1 | 2 | 2 | 0 |
Fmin =180+105+60+90+20=455
3.2. Расчёт сетевого графика
Сетевая модель называется сетевым графиком, на котором в определённом порядке показаны все операции по созданию объекта. Векторы или нити на графике – это выполняемые работы. Узлы – это события, т.е. момент начала или окончания ряда работ. Сетевой график в отличие от линейного даёт не только перечень работ, но и взаимосвязь между ними. На основе расчёта графика контролируется ход работ, основное внимание уделяется критическим работам, для остальных рассчитывается резерв времени. В основу построения сети закладывают три понятия: работа, событие, путь.
Основные расчётные параметры – ранние и поздние сроки начала и окончания работы, и резервы времени.
Рассмотрим фрагмент графика.
|
|
|
|
|
|
|
i-j- данная работа
t-j- время данной работы
h-i- предшествующая работа
j-k- последующая работа
tkp - время критического пути
tij PH - раннее начало данной работы
tij PO - раннее окончание данной работы
tij ПН - позднее начало работы
tij НО - позднее окончание данной работы
Rij - общий или полный резерв, времени работы
Rij - частный резерв времени работы
Раннее начало исходных работ полагается равное нулю. T 1 i РН = 0
Раннее окончание любой работы равно сумме её раннего начала и продолжительности.
tij PP = tij PH + tij
Раннее начало любой работы равно max раннему окончанию предшествующих работ.
tij PH = maxh th PO
max ранее окончание завершающих работ равно критическому времени
maxj tjN PO = t кр .
Позднее окончание завершающих работ - равно критическому времени. Позднее окончание работ. Позднее начало любой работы равно разности её позднего окончания и продолжительности: tij ПН = tij НО - tij
Позднее окончание любой работы равно min- му позднему началу последующих работ:
tij НО = mink tjk ПН
Все параметры сетевого графика не отрицательны.
Для работ критического пути ранние поздние параметры совпадают.
Полный резерв времени показывает насколько можно увеличить продолжительность данной работы не увеличивая t- критическое.
|
|
Частный или свободный резерв времени показывает, на сколько можно увеличить продолжительность данной работы, не изменяя раннего начало последующих работ.
Частный резерв равен разности раннего начала последующих работ и раннего окончания данной работы.
rij = tjk рн - tij ро
riN = t кр - tjN ро
rij![]() Rij
Rij
![]() Все расчёты записываются в таблицу - критический путь.
Все расчёты записываются в таблицу - критический путь.
Код работы |
Длит. работы |
Тр.н. | Тр.о. | Тп.н. | Тп.о. | Общ. резерв |
Частн. резерв |
| 1-2 | 4 | 0 | 4 | 0 | 4 | 0 | 0 |
| 1-3 | 5 | 0 | 5 | 8 | 13 | 8 | 6 |
| 1-7 | 3 | 0 | 3 | 11 | 14 | 11 | 11 |
| 2-3 | 7 | 4 | 11 | 6 | 13 | 2 | 0 |
| 2-4 | 9 | 4 | 13 | 10 | 19 | 6 | 4 |
| 2-7 | 10 | 4 | 14 | 1 | 14 | 0 | 0 |
| 2-8 | 8 | 4 | 12 | 13 | 21 | 9 | 6 |
| 3-4 | 6 | 11 | 17 | 13 | 19 | 2 | 0 |
| 3-5 | 8 | 11 | 19 | 19 | 27 | 8 | 0 |
| 4-5 | 0 | 17 | 17 | 27 | 27 | 10 | 2 |
| 4-8 | 1 | 17 | 18 | 20 | 21 | 3 | 0 |
| 4-10 | 20 | 17 | 37 | 19 | 39 | 2 | 2 |
| 5-6 | 11 | 19 | 30 | 27 | 38 | 8 | 0 |
| 5-10 | 9 | 19 | 28 | 30 | 39 | 11 | 11 |
| 5-12 | 7 | 19 | 26 | 39 | 46 | 20 | 20 |
| 6-11 | 4 | 30 | 34 | 40 | 44 | 10 | 10 |
| 6-12 | 8 | 30 | 38 | 28 | 46 | 8 | 8 |
| 7-8 | 0 | 14 | 14 | 21 | 21 | 7 | 4 |
| 7-9 | 10 | 14 | 24 | 14 | 24 | 0 | 0 |
| 8-9 | 3 | 18 | 21 | 21 | 24 | 3 | 3 |
| 8-10 | 7 | 18 | 25 | 32 | 39 | 14 | 14 |
| 9-10 | 15 | 24 | 39 | 24 | 39 | 0 | 0 |
| 10-11 | 5 | 39 | 44 | 39 | 44 | 0 | 0 |
| 11-12 | 2 | 44 | 46 | 44 | 46 | 0 | 0 |
Решение
1-2-7-9-10-11-12
Ткрит = 46
![]()
Заключение
Современные офисные пакеты
ArjFolder 2.85
Бесплатный архиватор ArjFolder, созданный независимым французским программистом Рафаэлем Мунье, предназначен, как нетрудно догадаться по названию, для работы с ARJ-файлами. Фактически ArjFolder с помощью функций Проводника Windows 9x строит программную оболочку для DOS-утилиты Arj (эта вызываемая из командной строки утилита входит в состав дистрибутива; вообще говоря, она распространяется условно-бесплатно, так что называть ArjFolder бесплатным пакетом не совсем правильно). Дистрибутив ArjFolder представляет собой самораспаковывающийся EXE-модуль объемом 730 Кбайт. В ходе инсталляции пользователю предлагается установить ArjFolder вместе с утилитой Arj или без нее. Для полноценной работы с архивами следует выбрать первую возможность, в противном случае программа не сможет формировать и пополнять архивы, а ограничится только просмотром содержимого архивов и их распаковкой. После инсталляции архиватор встраивается в Проводник Windows 9x. В системном меню "Пуск| Программы" появляется раздел с программой настройки ArjFolder, предназначенной для управления привязкой архиватора к файлам распознаваемых им типов (программа позволяет создавать, пополнять и распаковывать ARJ-файлы, а также просматривать и распаковывать сжатые файлы и архивы в форматах ACE, ZIP, GZIP, TAR, CAB и RAR). Кроме того, в контекстное меню объектов Windows добавляется команда Add to Arj ("Включить в Arj-архив"). С ее помощью можно создавать или пополнять ARJ-архивы и самораспаковывающиеся EXE-файлы. В случае если с программой связан какой-нибудь из распознаваемых ею типов файлов, щелчок на таком файле вызывает двухпанельное окно, похожее на Проводник (к сожалению, это единственный и не очень удобный способ вызвать ArjFolder). Упакованные в архиве объекты изображаются в правой панели окна подобно содержимому обычной папки. Контекстные меню позволяют открывать, распаковывать, удалять или просматривать эти файлы. Добавлять файлы в ARJ-архив и распаковывать их можно с помощью перетаскивания, для остальных типов архивов перетаскиванием можно только распаковывать файлы. Из богатейшего ассортимента опций командной строки, предусмотренных в DOS-программе Arj, Windows-оболочка задействует лишь несколько основных, в частности возможность создавать многотомные архивы для записи на дискеты, защиту с помощью пароля, упаковку вложенных каталогов, упаковку скрытых и системных файлов (опции действуют при создании нового архива). К сожалению, интеграция архиватора с Windows недостаточно полна: если в программах типа ZIP Magic или WinRAR (да и в файловых оболочках типа DISCo Commander) архивы по своему "поведению" практически неотличимы от обычных каталогов, то оснащенный средствами ArjFolder Проводник в левой панели показывает вместо дерева дисков и каталогов только один архив, не имеющий контекстного меню, а в практически бесполезной строке адреса может содержаться только имя текущего архива. На панели инструментов при этом отсутствует кнопка перехода к родительскому каталогу, и, что самое неприятное, - в меню Файл нет команды Открыть. Все операции с архивами производятся в текстовом окне DOS, что тоже не очень удобно. Еще один недостаток - программа не показывает структуру упакованных каталогов, изображая содержимое архива в виде единого плоского списка (впрочем, это свойственно большинству рассмотренных программ). Следует также заметить, что отдельные элементы интерфейса (в целом англоязычного) остались не переведенными с французского (так, вместо привычного обозначения MB вы увидите Mo). Для пользователей Windows, имеющих дело с несложными ARJ-архивами и избегающих командных строк, данная программа может стать простым бесплатным решением, остальные, скорее всего, предпочтут что-нибудь более совершенное, например программу WinRAR с подключенным внешним модулем Arj.
Список используемой литературы:
1. Конспект лекций по информатике
2. Методические указания к лабораторным работам
3. Журнал «Мир ПК»