Реферат: Компьютерные технологии решения оптимизационных задач управления

Содержание

1. Компьютерные технологии решения оптимизационных

задач управления 3

2. Обзор задач методов и пакетов приложений интегрированных математических сред 7

3. Понятие о численных методах лежащих в основе компьютерной реализации процесса принятия оптимизационных решений 15

4. Идеи методов одномерной оптимизации 18

Список использованной литературы 26

1. Компьютерные технологии решения оптимизационных задач управления

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Задачи оптимизации - это задачи нахождения максимального или минимального значения некоторой функции, называемой целевой функцией. Если заданы ограничения на аргументы данной функции, то задача называется задачей условной оптимизации, если ограничения не накладываются, то задачей безусловной оптимизации.

Большое распространение получили задачи линейного программирования- задачи, в которых линейны как целевая функция, так и ограниченная в виде равенств или неравенств. Линейное программирование тесно связано с другими методами математического программирования. На практике часто приходится встречаться со случаями, когда целью оптимизации является установление наилучшей последовательности те6х или иных работ, такие задачи называют задачи динамического программирования. В других задачах оптимизации, в качестве переменных выступают функции - вариационные задачи. Существуют задачи оптимизации с несколькими целевыми функциями - задачи системной оптимизации.

Для решения задач данного типа применяются такие методы как:

1) Симплекс-метод,разработанный Danzig'oM около 50 лет назад, перебирает "базисные" решения, построенные путем фиксирования достаточного количества переменных, чтобы матрица системы ограничений Ах = b стала квадратной. Такая полученная система может быть решена для единственных значений оставшихся переменных. Базисные решения являются экстремальными граничными точками области допустимых решений, определяемой системой ограничений, и симплекс-метод может рассматриваться как прохождение от одной такой точки к другой по границе области.

2) Метод барьеров или внутренних точек,с другой стороны, обходит точки из внутренней части области допустимых значений. Эта группа
методов происходит от технологий нелинейного программирования, разработанных и популяризованных в 60-х гг. Fiacco и McCormick, но их приложения к линейному программированию датируются только 1984 г.

3) Родственная ЛП задача целочисленного программирования(или
целочисленного линейного программирования, точнее говоря) допускает
только целочисленные значения переменных. Задачи ЦП обычно ближе к реальным задачам, чем задачи ЛП, но намного более трудоемки в решении.
Наиболее широко используемые методы решения задач ЦП используют решение серии задач ЛП, чтобы найти целочисленные решения и доказать оптимальность. Поэтому большая часть ПО ЦП построена на базе ПО ЛП, и данный FAQ применим для решения задач этих двух видов.

Линейное и целочисленное программирование пригодно для моделирования множества различных проблем в планировании, маршрутизации, разработке расписаний, назначениях и дизайне. ЛП и его расширения используются в транспортной индустрии, энергетике и машиностроении.

В жизни решение задач оптимизации занимает очень много времени и это достаточно трудоемкий процесс, где необходимо учесть все параметры. И чтобы облегчить нам работу по поиску оптимума программисты разных стран написали большое количество программ для решения задач оптимизации практически во всех отраслях производства и сферах нашей жизни.

Система Mathematica объединяет в себе запас мировых математических знаний, накопленных в справочной литературе, и использует свои собственные

революционные алгоритмы, чтобы развивать эти знания.

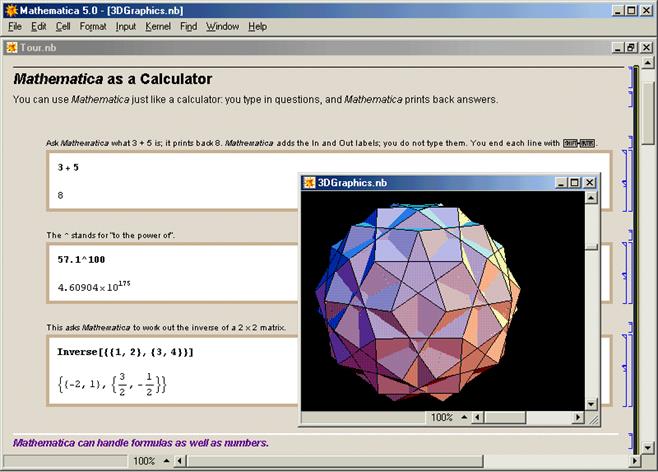
Рис.1 – Интерфейс программы Mathematica

Умение проводить аналитические расчеты — одно из главных достоинств этой программы, автоматизирующей математические расчеты. Mathematica умеет преобразовывать и упрощать алгебраические выражения, дифференцировать и вычислять определенные и неопределенные интегралы, вычислять конечные и бесконечные суммы и произведения, решать алгебраические и дифференциальные уравнения и системы, а также разлагать функции в ряды и находить пределы

Int=Integrate [a*x^5/Sqrt[x^3-1], x]

Во многих видах вычислений система Mathematica является мировым рекордсменом по скорости.

Mathematica позволяет строить двух и трехмерные графики различных типов в виде точек и линии на плоскости, поверхностей, а также контурные, градиентные (dencityplot), параметрические. Mathematica выполняет построение графика в три этапа. На первом создается множество графических примитивов, на втором они преобразуются в независимое от вычислительной платформы описание на языке PostScript, а на третьем это описание переводится в графический формат для той системы, на которой установлена Mathematica.

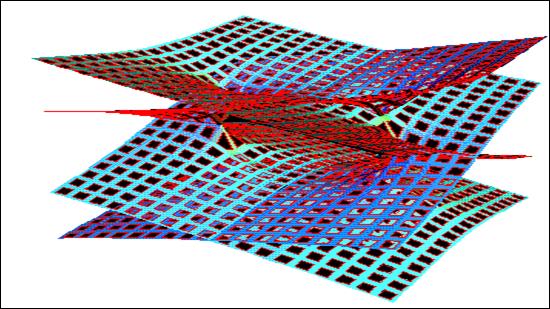
Рис.2 – 3D-график

Другая сторона развития программного обеспечения — ориентация на “непрограммирующего пользователя”. В этом случае пользователь такого пакета получает возможность сосредоточиться на сущности самой задачи, а не способах ее программной реализации. В свою очередь пользователь должен ясно представлять возможности используемого пакета и заложенных в нем методов, а также уметь выбрать необходимый пакет, соответствующий решаемой задаче.

Все этапы создания и использования математической модели легко проследить при работе с пакетом MATHCAD фирмы “MathSoft Inc.” (USA).

2. Обзор задач методов и пакетов приложений интегрированных математических сред

Современные пакеты обработки печатной продукции включают средства оформления текста, подготовки математических формул, графиков, схем, таблиц. Современные информационные технологии позволяют подготовить документ, который может включать как объекты документы других типов или гиперссылки на другие документы и программы обработки.

Персональные компьютеры получили наибольшее применение (по количеству) в задачах моделирования. Их изначально широкое использование определялось, прежде всего, не их быстродействием, а возможностью гармонично настроить рабочее место исследователя, организовать передачу данных между задачами, получить хорошо оформленный отчет.

Наконец, современное развитие информационных технологий, ориентированных на создание интегрированных пакетов мультимедиа-технологии, привело к появлению компьютерных математических систем, к которым относятся Maple V фирмы Waterloo Maple Software Inc.

Системы компьютерной алгебры (СКА) очень многочисленны, однако не более десяти из них являются по-настоящему современными, общими и достаточно распространёнными. СКА отличаются друг от друга количеством встроенных функций; в некоторых системах их имеется несколько десятков, в других – на порядок больше. Внутренние структуры этих систем существенно отличаются одна от другой. Тем не менее, большинство СКА обладают следующими общими свойствами:

- все они имеют набор так называемых встроенных функций (базисных предпрограммируемых команд), которые предназначены для вычислений (численных, символьных, графических);

- работа пользователя со встроенными функциями происходит в интерактивном режиме; пользователь имеет возможность вмешиваться в ход вычислений в любой момент;

- входные данные представляют собой выражения, у которых, по меньшей мере, исходное представление выдержано в стандартных математических обозначениях; ввод этих данных в систему производится либо в таком же виде, либо с использованием специфического для каждой конкретной СКА синтаксиса;

- система содержит язык пользователя – совокупность встроенных функций и их опций, а в некоторых СКА, к тому же, предоставляют возможность определения процедур с помощью операторов классических языков программирования (If, While и др.);

- СКА являются открытыми для пользователя системами, иначе говоря, пользователь может создавать новые функции на основе встроенных функций.

- вычислительное ядро имеет структуру списка или дерева, а управление памятью — динамическое, с автоматическим восстановлением доступного пространства;

- язык реализации системы скрыт от пользователя (содержится в так называемом вычислительном ядре системы); это чаще всего С или Lisp (иногда Pascal);

Компьютерные математические системы дают пользователю возможность использовать встроенный язык программирования сверхвысокого уровня, позволяющий расширять класс задач, охваченных встроенными функциями, и решать такие задачи, которые невозможно решить в рамках использования встроенных функций.

Далее мы рассмотрим программное обеспечение персональных компьютеров, используемое на различных этапах математического моделирования.

За последние годы чётко сформировалась следующая тенденция в развитии программного обеспечения для персональных ЭВМ: появляется всё больше интегрированных пакетов, которые включают наряду со специализированными программами и программы подготовки отчетов. Модульный подход к моделированию прослеживается и в современных пакетах.

Одним их из них является MatLab (“The MathWorks Inc”, USA), который, по существу, изначально предназначался для “больших” машин, а затем был адаптирован для персональных компьютеров.

Система MatLab

Данная система ориентирована на матричные и векторные вычисления (её названием является сокращение словосочетания Matrix Laboratory) и предназначена в основном для численного моделирования технических систем. Её последние версии содержат элементы универсальных систем компьютерной алгебры: специальный модуль MatLab Notebook, позволяющий, в том числе, использовать возможности Microsoft Word для оформления документов, а также приобретённый у компании Maple Waterloo модуль основной символьной библиотеки системы Maple V 4.0 для выполнения некоторых аналитических расчётов. Входной язык в определённой мере напоминает BASIC (с элементами Фортрана и Паскаля). Интерфейс менее доступный и красочный, чем у системы MathCAD, однако скорость вычислений выше.

Использование в образовании нецелесообразно; система предназначена для профессиональной работы в области математики и смежных областях.

Система MatLab предназначена для выполнения инженерных и научных расчетов и высококачественной визуализации получаемых результатов. Эта система применяется в математике, вычислительном эксперименте, имитационном моделировании.

В пакет входит множество хорошо проверенных численных методов (решателей), операторы графического представления результатов, средства создания диалогов. Отличительной особенностью MatLab по сравнению с обычными языками программирования является матричное представление данных и большие возможности матричных операций над данными. Используя пакет MatLab можно, как из кубиков конструктора, построить довольно сложную математическую модель, или написать свою программу (весьма похожую на Фортран-программу). А можно используя SIMULINK и технологию визуального моделирования составить имитационную модель или систему автоматического регулирования.

Гибкий язык MatLab дает возможность инженерам и ученым легко реализовывать свои идеи. Мощные численные методы и графические возможности позволяют проверять предположения и новые возникающие идеи, а интегрированная среда дает возможность быстро получать практические результаты.

Сегодня MatLab используется во множестве областей, среди которых обработка сигналов и изображений, проектирование систем управления, финансовые расчеты и медицинские исследования. Его открытая архитектура делает возможным использование MatLab и сопутствующих продуктов для исследования данных и создания собственных инструментов, использующих функциональные возможности MatLab.

Другая сторона развития программного обеспечения – ориентация на менее профессионально подготовленного, “непрограммирующего пользователя”. В этом случае пользователь такого пакета получает возможность сосредоточиться на сущности самой задачи, а не способах ее программной реализации. Однако, в свою очередь, пользователь должен ясно представлять возможности используемого пакета и заложенных в нем методов, а также уметь выбрать необходимый пакет, соответствующий решаемой задаче. Все этапы создания и использования математической модели легко проследить при работе с популярным пакетом MathCAD (фирма “MathSoft Inc.”, USA).

MATHCAD — универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Математическое обеспечение пакета позволяет решать многие задачи в объеме инженерного вуза.

Разработчики пакета совершенствуют пакет от версии к версии. В настоящее время существет версия MATHCAD 13, обладающая еще большими возможностями. Существуют оригинальная (англоязычная) и русифицированная версии программы.

Что отличает пакет MATHCAD от калькулятора: вычисление с произвольной точностью, работа с различными типами данных (комплексные, векторы, матрицы), использование библиотеки математических функций (которая может быть дополнена программами на ФОРТРАНе).

Основное преимущество пакета перед типичными языками программирования — естественный математический язык, на котором формулируется решаемая задача.

Пакет объединяет в себе: редактор математических формул, интерпретатор для вычислений, библиотеку математических функций, процессор символьных преобразований, текстовый редактор, графические средства представления результатов. Пакет MATHCAD относится к интегрированным пакетам, т.е. позволяет не только произвести вычисления, но и получить документ - итоговый отчет с комментариями, формулами, таблицами и графиками. В отличие от издательских систем формулы в MATHCAD работают.

К положительным качествам MATHCAD следует отнести открытость - все приведенное в документе может быть воспроизведено, а интеграция в одном документе исходных данных, метода решения и результатов позволяет сохранить настройки для решения подобных задач.

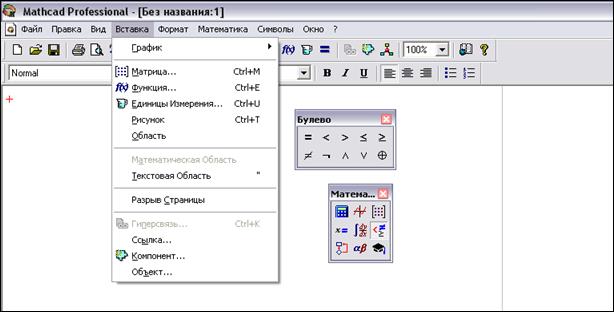
Рис. 3 – Интерфейс программы Mathcad

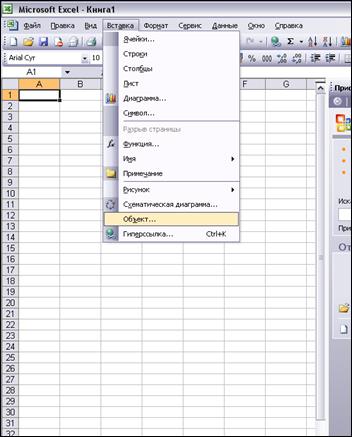
Рис. 4 – Интерфейс программы Microsoft Excel

Программа MS Excel является лидером на рынке программ обработки электронных таблиц, определяет тенденции развития в этой области.

Одним из важнейших функциональных расширений программы, предназначенным для профессионалов, является встроенная в Excel Среда программирования Visual Basic (VBA) для решения прикладных задач.

Основные возможности программы MS Excel:

1. Управление файлами

2. Построение таблиц

3. Табличные вычисления

4. Построение и оформление диаграмм

5. Вставка более 200 функций

6. Обмен данными

7. Обработка списков

8. Анализ данных

9. Конфигурирование программы MS Excel

10. Встроенный язык VBA

11. Решение задач оптимизации с использованием надстройки Поиск решения

Система REDUCE

Данная система хронологически сможет считаться одной из старейших систем компьютерной алгебры, её первая версия появилась в 1969 г. Входной язык по характеру аналогичен языкам программирования. Для решения задачи требуется составить программу, которая состоит из серии команд, представляющих собой вызовы функций, условные операторы, циклы и т. п. Система при переходе к каждому следующему этапу интерпретирует команду в порядке поступления и выполняет её.

Система REDUCE рассчитана на профессиональное использование при сложных вычислениях, имеет большую библиотеку функций и реализуется на “больших” ЭВМ, что делает её применение в образовании практически невозможным.

Система Macsyma.

Система Macsyma, как и REDUCE, структурирована по образцу высокоуровневых языков программирования. Её новая версия (Macsyma 2.3) обладает рядом интересных особенностей, к которым можно отнести применение самых современных алгоритмов численных расчётов библиотек, таких как LINPACK и EISPACK, благодаря встроенным в систему командам программы MatLab. Кроме того, имеется встроенная электронная таблица для обработки данных и специальное мощное, взаимосвязанное с интерфейсом Macsyma, дополнение, предназначенное для решения дифференциальных уравнений с частными производными методом конечных элементов. Как и REDUCE, данная система рассчитана на использование математиками-профессионалами.

Система Derive

Система Derive, на взгляд многих пользователей, очень органично сочетает возможности проведения численных и символьных вычислений с простотой в обращении и невысокими требованиями к используемой компьютерной технике. Последнее обстоятельство является особенно существенным аргументом в пользу применения данной системы в образовании. Derive имеет многооконный интерфейс пользователя и удобную систему меню. Языком реализации является “Lisp” — один из самых известных функциональных языков, ориентированный на решение задач искусственного интеллекта и построение экспертных систем. Ввод математических символов выполняется с клавиатуры набором слов, которые порождают на мониторе изображения соответствующих математических символов, при необходимости — в двумерном виде (как, например, обыкновенные дроби). Встроенный графический редактор позволяет получать двумерные графики в декартовых и полярных системах координат и трёхмерные графики, с возможностью автоматического масштабирования.

Существенным достоинством современных версий Derive является то, что они относятся к расширяемым системам, способным адаптироваться к решению конкретных задач, формулируемых данным пользователем.

Однако недостатком системы Derive является ограниченная возможность для программирования пользователем. Использование системы Derive в образовании возможно, и это сегодня уже реализуется в некоторых вузах и даже школах.

3.Понятие о численных методах лежащих в основе компьютерной реализации процесса принятия оптимизационных решений

Разнообразие нелинейных задач математического программирования (с полной или неполной информацией) вызывает необходимость разработки методов оптимизации, не связанных непосредственно с анализом условий существования X* и целиком базирующихся на вычислительных и логических операциях.

Идеи этих методов обычно просты; как правило, они следуют из эвристических соображений, сводя проблему решения задачи к построению надлежащего алгоритма поиска X*, г*, причем желаемые свойства таких алгоритмов оговариваются заранее.

Численные методы играют значительную роль в решении важных для практики оптимизационных решений.

В отдельных случаях бывает трудно определить, к какому классу относится та или иная задача и существует ли для нее обоснованный метод решения.

На выбор метода может влиять стремление максимально использовать мощности ЭВМ с целью снижения затрат на исследования (если подобная перспектива реальна).

Указанные обстоятельства позволяют рассматривать численные методы оптимизации как необходимое средство решения проблем поиска оптимума в исследованиях, различных по содержанию и сложности.

Рассмотренные положения позволяют обосновать приемлемость тех или иных численных методов для решения экстремальных задач.

Вычисление определенных интегралов.

Рассмотрим пример: .

В первую очередь необходимо создать функцию,вычисляющую подынтегральное выражение.

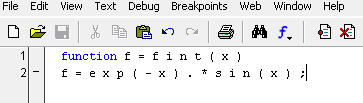
Для вычисления интеграла вызовем функцию quad, задав первым аргументом ссылку на функцию fint, а вторым и третьим — нижний и верхний пределы интегрирования.

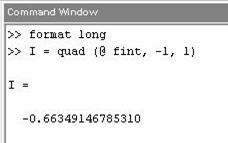
По умолчанию функция quad вычисляет приближенное значение интеграла с точностью 10-6. Для изменения точности вычислений следует задать дополнительный четвертый аргумент:

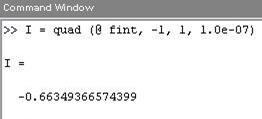
Вычисление двойных интегралов.

В MATLAB определена функция dblquad для приближенного вычисления двойных интегралов. Как и в случае вычисления определенных интегралов, следует написать файл-функцию для вычисления подынтегрального выражения. Вычислим интеграл:

Следовательно, функция должна содержать два аргумента x и y:

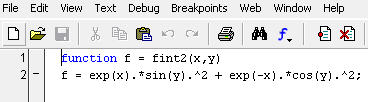
Функция dblquad имеет пять входных аргументов. При ее вызове необходимо учесть, что первыми задаются пределы внутреннего интеграла по х, а вторыми — внешнего по у:

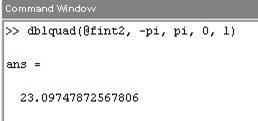
Интегралы, зависящие от параметра.

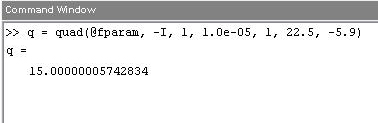
Функции quad и quadl позволяют находить значения интегралов, зависящих от параметров. Аргументами функции, вычисляющей подынтегральное выражение, должна быть не только переменная интегрирования, но и все параметры. Значения параметров указываются через запятую, начиная с шестого аргумента quad или quadl.

Решим интеграл:

Зададим функцию

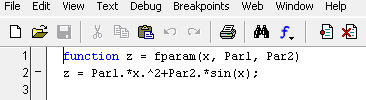
Используя quad, вычислим интеграл:

4.Идеи методов одномерной оптимизации

Численные методы оптимизации классифицируются следующим образом.

1. По размерности решаемых задач: одномерные; многомерные.

Одномерная оптимизация: Метод сканирования. Метод деления пополам. Метод золотого сечения. Метод параболической аппроксимации.

Многомерная безусловная градиентная оптимизация: Метод градиента. Метод наискорейшего спуска. Метод сопряженных градиентов. Метод тяжелого шарика.

Многомерная безградиентная оптимизация: Метод Гаусса-Зайделя (покоординатный спуск). Метод Розенброка. Симплексный метод (метод дифференцируемого многогранника). Метод параллельных касательных.

Многомерная случайная оптимизация: Метод слепого поиска. Метод случайного направления. Метод поиска с «наказанной случайностью». Метод с «блуждающим» поиском.

Многомерная условная оптимизация: Метод штрафов. Метод прямого поиска с возвратом. Метод проектирования градиента.

Постановка: требуется оптимизировать х (формальная постановка)

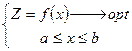
- функция одной переменной

- целевая функция.

Решение: найти х, при котором принимает оптимальное значение.

2 варианта:

- минимизировать – задача минимизации;

- максимизировать – задача максимизации.

Рассмотрим случай минимизации

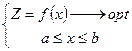
2 способа:

- аналитический

- численный

В аналитическом задается в виде формулы, в численном задается в виде черного ящика, на входе подается х, на выходе значение целевой функции в этой точке.

Пусть функция определена в некоторой области S (), в случае одномерной оптимизации S – интервал :

1. точка называется глобальным минимумом, если для

2. точка называется строгим глобальным минимумом, если для

3. точка называется локальным минимумом, если для

4. точка называется строгим локальным минимумом, если для

Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.

Аналитический способ нахождения локального минимума.

- дифференцируема

- необходимое условие точки локального минимума.

Численные методы

Пусть функция задана на интервале , при этом существует такая точка , что на – монотонно убывает, а на – монотонно возрастает, то функция унимодальная.

а b

Если из того что следует, что , то функция называется монотонно возрастающей. Если из того что следует, что , то функция называется монотонно убывающей.

Методы одномерного поиска

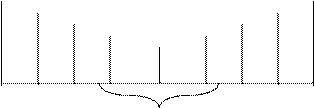
Разобьем и вычислим значение функции в каждой точке.

искомый минимум

В результате остается интервал меньшего размера, к которому применяется тот же метод, и находим еще один интервал, в конце находим интервал с заведомо нужной точкой.

Интервал неопределенности – интервал, в котором заведомо находится точка минимума. Наиболее эффективное разбиение – двумя точками на 3 равных отрезка.

- после выполнения n шагов сокращение исходного интервала

- точность с которой надо найти решение задачи.

N=2n, где n – число шагов, N – число вычислений (мера эффективности данного решения).

Метод золотого сечения

Точки должны быть расположены на равном расстоянии.

а b

; ; ;

; - золотое сечение.

- величина сокращения на каждом шаге

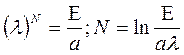
число итераций растет как логарифм функции.

Одномерная оптимизация с использованием производных

. Пусть целевая функция дифференцируема .

точка локального минимума

точка локального максимума

точка перегиба

Методы для нахождения корня уравнения функции 1-ой производной от исходной

Нахождение локального минимума или максимума сводится к нахождению корней первой производной от данной

f ’( x )=0

Если f’(x) представляет собой многочлен, то уравнение называется алгебраическим (полиномиальным), если f’(x) представлена тригонометрическими, логарифмическими, показательными и т.п. функциями, то уравнение называется трансцендентным .( вдальнйшем вместо f ’( x ) будем употреблять f ( x ) )

Решение уравнения вида разбивается на два этапа:

1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2. вычисление выделенного корня с заданной точностью.

На первом этапе может помочь построение приближенного графика функции f(x) или, если функция достаточно сложная, то можно попытаться представить уравнение в виде и построить два графика и , тогда корнями уравнения будут абсциссы точек пересечения этих кривых.

Выбор интервалов, в которых имеется один и только один корень производится на основании известных свойств непрерывных функций:

- Если на концах некоторого интервала функция непрерывна и принимает значения разных знаков, т.е. , то на этом интервале уравнение имеет хотя бы один корень (один или нечетное количество корней).

- Если на концах интервала функция принимает значения одинаковых знаков, т.е. , то на этом интервале уравнение не имеет корней или имеет четное количество корней.

- Если на интервале первая и вторая производные функции сохраняют определенный знак, т.е. и или и , и не обращаются в нуль на всем участке, то функция монотонна, и корень будет единственным.

Для вычисления выделенного корня существует множество приближенных методов. Все они вычисляют значение корня уравнения с заданной степенью точности , т.е. заданное количество цифр после запятой. Рассмотрим следующие методы:

- половинного деления;

Метод половинного деления

Суть метода половинного деления (дихотомии) заключается в следующем.

Отрезок делится пополам и за первое приближение корня принимается точка c , которая является серединой отрезка, т.е.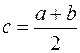. Если , это корень уравнения. Если нет, то далее выбирается тот из отрезков [a , c ] или [c , b ], на концах которого функция имеет разные знаки. Полученный отрезок снова делится пополам, и проводятся те же рассуждения. Деление продолжается до тех пор, пока длина отрезка не станет меньше заданного .

Метод половинного деления реализуется в виде следующего алгоритма:

Найти точку c = (a + b )/2.

Если f (a )×f (c ) <0, то корень лежит на интервале [a , c ], если нет, то корень лежит на интервале [c , b ].

Если величина интервала не превышает некоторое достаточно малое число е , то найден корень с точностью е , иначе возврат к п.1.

Несмотря на простоту, этот метод требует слишком большого количества вычислений и не всегда позволяет найти решение с заданной точностью.

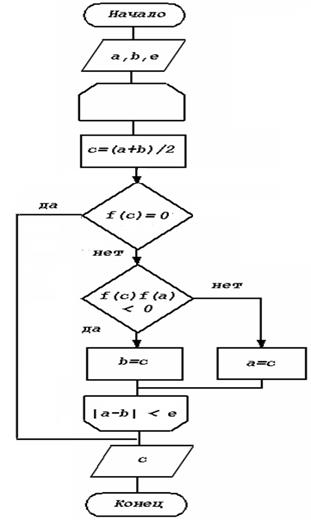
Блок-схема алгоритм решения уравнения методом деления пополам.

Список использованной литературы

1. Автоматизация вычислений и компьютерное моделирование. MS Excel и MathCad : учебное пособие / Н.В. Вознесенская. – Саранск : Изд-во Мордовского университета, 2004. – 91 с.

2. Дьяконов, В. MathCad 2001: специальный справочник / В. Дьяконов. – СПб. : Питер, 2002. – 832 с.

3. Информатика : учебник / Макарова Н. В. [и др.]. – М. : Финансы и статистика, 1997. —768с.

4. Исследование операций в экономике: Учебное пособие для вузов / Кремер Н.Ш. [и др.]. – М.: ЮНИТИ, 2002. – 407 с.

5.Кудрявцев, Е. Н. Исследования операций в задачах, алгоритмах и программах / Е.Н. Кудрявцев. М., Наука, 1982. – 150 с.

6.Кузнецов, Ю. Н. Математическое программирование / Ю.Н. Кузнецов, В.И. Кузубов, А.В. Волощеноко. - М.: Высшая школа, 1980. – 320 с.

7. Леонтьев, Ю. Microsoft Office 2000. Краткий курс / Ю. Леонтьев. – СПб.: Питер, 2001. – 760 с.

8.Сидоров, М. Е. Решение задач оптимального планирования в таблицах Excel // Информатика и образование. – М., 2001. – № 1. – с. 36 – 51.

9.Стандарт предприятия. Общие требования и правила оформления курсовых и дипломных работ и пояснительных записок к курсовым и дипломным проектам.

10.Ширяев, В.Д. Экономико-математические методы: учебное пособие / В.Д. Ширяев, Н.М. Куляшова. – Саранск : Изд-во Мордовского университета, 2002. – 112 с.

11.Экономическая информатика: Учебник / Косарев В.П.. – М.: Финансы и статистика, 2004. – 592 с.