| Скачать .docx |
Курсовая работа: Программирование и основы алгоритмизации
Федеральное агентство образования Российской Федерации
Тульский государственный университет
Кафедра «Системы автоматического управления»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине
«Программирование и основы алгоритмизации».
Разработал студент группы 120161
Матях Р.И.
Проверил доцент кафедры САУ:
Илюхин А. С.
Тула 2007 г.
ЗАДАНИЕ
По заданной структурной схеме САУ составить систему ДУ, описывающих её функционирование.
Разработать программу на языке Pascal для решения этой системы методом Эйлера.
Разработать программу на языке Pascal для построения графиков переходных процессов.
Провести исследование влияния конструктивных параметров на величину времени регулирования при подаче на вход системы единичного ступенчатого сигнала.
Общий вид функциональной схемы САУ
|
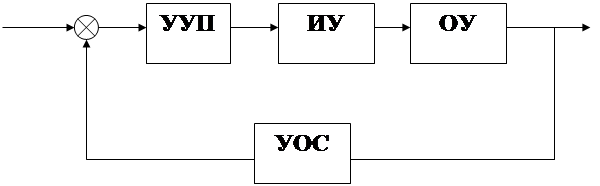
Обозначения:
СУ – суммирующее устройство;
УУП – устройство усиления и преобразования;
ИУ – исполнительное устройство;
ОУ – объект управления;
УОС – устройство обратной связи;
g – управляющее воздействие;
έ – сигналрассогласования;
u – сигнал на выходе УУП;
α – координата исполнительного органа исполнительного устройства;
y – регулируемая величина;
z – сигнал обратной связи.
Варианты УУП:
1. Пропорциональный регулятор
![]()
2. Пропорциональный интегральный регулятор

3. Пропорциональный дифференциальный регулятор

4.Интегрально-дифференциальный регулятор

5. Пропорциональный интегрально-дифференциальный регулятор

Варианты схем исполнительных механизмов:
1. Двигатель постоянной скорости
![]()
2. Автоматический привод

3. Автоматический привод
![]()
Варианты объектов управления:
W(p)=K4/((T4*p+1)*(T5*p+1)*(T6*p+1))
W(p)=K4/(T42 *p2 +2*η*T4*p+1)
W(p)=K4/(p*(T4*p+1)*(T5*p+1))
W(p)=K4/(p*(T42 *p2 +2*η*T4*p+1))
W(p)=K4/((T4*p+1) (T52 *p2 +2*η*T5*p+1))
W(p)=K4/((T4*p+1)*(T5*p+1))
W(p)=K4/(p*(T4*p+1))
Передаточная функция:
W(p)=K6
1. Решение дифференциальных уравнений методом Эйлера
1.1 Описание метода
Уравнения, содержащие производные от функции, возникают при решении многих научно-технических задач, причем существует большое разнообразие классов подобных уравнений. Для решения некоторых из них могут быть использованы аналитические методы, рассматриваемые в курсах математики, однако в большинстве случаев приходится применять численные методы.
Сначала рассмотрим один из простейших классов дифференциальных уравнений, на примере которого будут показаны особенности использования численных методов.
Пусть задано дифференциальное уравнение первого порядка с начальным условием (задача Коши)
dy / dx = F ( x , y ), (1)
У(x0 ) = Уо (2)
где F ( x , y ) – заданная функция двух переменных x и у , x0 , у0 – известные числа. Требуется определить функцию у = у(x) при х=> x 0 . Уравнение (1) можно рассматривать как задание кривой через ее производную в координатной плоскости x, у , поскольку известно как вычислить производную в каждой точке этой кривой через ее координаты. В общем случае уравнению (1) удовлетворяет целое семейство кривых; начальное условие (2) позволяет выбрать из этого семейства одну определенную кривую, которая проходит через заданную точку x 0 , y 0 .
Для численного решения (1) , (2) заменим область непрерывного изменения аргумента х дискретным множеством точек, т.е. введем сетку. Положим, что величина х изменяется от значения х= x 0 до значения х= b . Тогда, рассматривая равномерную сетку, получаем узловые точки x0 , x 1 ,… xk ,… b , находящиеся на расстоянии h друг от друга, т.е.
xk +1 - xk = h , k =0,1... , (3)
где h – шаг сетки. Соответствующие значения функции будем обозначать уk , т.е.
yk = y *( xk ).
Здесь у* (х) – функция, которая является приближенным решением (1), (2). Для получения численного решения, дифференциальное уравнение (1) заменяется уравнениями относительно значений функций у*(x) в узловых точках. Эти уравнения называются разностными. Простейшее разностное уравнение для (1) имеет вид
( yk +1 - yk )/ h = F ( xk , yk ) k =0, l ,... , (4)
Уравнение (4) следует из (1), если производную dy/ dx приближенно представить через значения функции у(x) в соседних узлах.
Соотношения (2.12.4) можно записать в виде
Yk +1 = yk + h * F ( xk , yk ). (5)
Тогда, учитывая (2), с помощью формулы (5) можно последовательно определить значения у1 ,y2 , .… Этот метод приближенного решения (1), (2) называется методом Эйлера. Геометрическая интерпретация этой схемы дана на рис.1 , где изображено поле интегральных кривых. Использование только первого члена формулы Тейлора означает движение не по интегральной кривой, а по касательной к ней. На каждом шаге мы заново находим касательную; следовательно, траектория движения будет ломаной линией. Из-за этого метод Эйлера иногда называют методом ломаных.

Рис.1
Доказывается, что если шаг сетки h стремится к нулю, то приближенное решение, определяемое (5), стремится к точному решению (1), (2), т.е. имеется факт сходимости приближенного решения к точному при h ®0. Однако в условиях реальных вычислений на компьютере при конечном шаге целесообразно знать насколько полученное приближенное решение близко к точному. В качестве меры отклонения (нормы ошибки) часто используют величину
d y = max | y ( xk ) – yk |. (6)
Здесь у(х) — строгое решение (1), (2) , yk — приближенное значение искомой функции в узловых точках xk , полученное путем решения разностных уравнений, например (4).
Для разностных уравнений величина d y оценивается формулой
d y ~ Chm (7)
Здесь С — const , зависящая от длины отрезка, на котором ищется решение, и способа дискретизации (1) , m – параметр, который называется порядком точности решения. Порядок точности метода Эйлера - минимальный, т.е. т = 1, что связано с довольно грубым способом аппроксимации дифференциального уравнения разностным. Как правило, чем выше порядок точности, тем более предпочтительным является численный метод.
Можно утверждать, что любое правильно составленное разностное уравнение аппроксимирует исходное дифференциальное с той или иной точностью. Качество аппроксимации обычно оценивают по точности, с которой решение исходной задачи удовлетворяет разностному уравнению, т.е. по формуле
Max | ( y ( xk +1 )- y ( xk ))/ h - f ( xk , y ( xk ))|<= Chm
где С - const, т — порядок аппроксимации разностного уравнения.
Сравнение (1) и (4) показывает, что метод Эйлера имеет первый порядок аппроксимации, так же как и точность решения. Однако в общем случае утверждение о равенстве порядков точности решения и аппроксимации разностного уравнения не является очевидным и требует доказательства. Метод Эйлера является одним из самых старых и широко известных методов численного решения дифференциальных уравнений. К сожалению, этот метод может приводить к недопустимо большим ошибкам, а кроме того, он часто оказывается неустойчивым — малая ошибка (происходящая при округлении или из-за неточности исходных данных) существенно увеличивается с ростом х .
1.2 Программная реализация метода Эйлера
Программа для решения дифференциальных уравнений состоит из трех частей:
Главная программа.
Процедуры, реализующие метод Эйлера.
Процедуры вычисления правых частей.
Процедура вычисления правых частей R имеет вид:
procedure R( var y0,F: mass);
begin
F[1]:=y0[2];
F[2]:=(ft-k2*y0[2]-k1*y0[1])/Mm
end;
где:
F – массив значений правых частей системы, приведенной к нормальной форме Коши;
y0 – массив значений начальных условий системы;
k1,k2 … kn – коэффициенты;
ft – f(t), т.е. сигнал (воздействие), подаваемый на вход системы;
Процедура, реализующая метод Эйлера:
procedureEu(vart0,t,h: real; varm:integer; vary0,y:mass);
var i: integer;
begin
R(y0,F);
for i:=1 to m do
y[i]:=y[i]+h*F[i];
t:=t+h;
end;
где:
t0,tk – начальное и конечное значение времени;
m – порядок системы;
h – шаг сетки;
После задания всем переменным определенных значений происходит последовательное вычисление значений функции
while t0<=tk do
begin
Eu(t0,t,h,g,y0,y);
writeln(t,y[1],y[2]);
for i:=1 to g do
y0[i]:=y[i];
end;
readln;
end.
Для приведённой выше схемы составим систему дифференциальных уравнений:
Выразим неизвестные величины через данные начальных условий
1. ![]() Но
Но ![]()
Итак, 
2. Аналогично
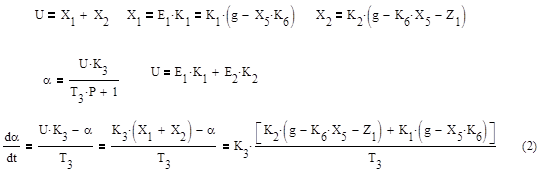
3. 
4. 
5. Пусть 
тогда ![]()
Таким образом имеем систему из пяти дифференциальных уравнений:
![]()

Итак, составим программу для решения дифференциальных уравнений и построения графиков переходных процессов.
Сначала сделаем некоторые переобозначения:
F — массив значений правых частей
F[1]=dZ1 /dt
F[2]=X6
F[3]=dα/dt
F[4]=dX4 /dt
F[5]=dX6 /dt
Y0 — начальные значения переменных системы уравнений
Y — массив переменных системы уравнений
Y[1]=Z1
Y[2]=X5
Y[3]= α
Y[4]=X4
Y[5]=X6
2. Листинг программы
Входные параметры:
* T0 * 0
* TK * 30
* h * 0.01
* Y0 * 0 0 0 0 0
* T * 1 2 1 1 1
* k * 1 1 1 1 1
* g * 1
* n * 0.5
********
2.1. Главная программа
programEler;
uses mdd, graph;
begin
start(ymin,ymax,t0,tk,t,k1,k2,k3,k4,t1,t2,t3,h,g,y0,y);
output1;
while t<=tk do
begin
Eu(g,k1,k2,k3,k4,k6,t1,t2,t3,t4,d,t,h,m,y0,F,y,Gr);
abc (Gr, ymin, ymax);
output(t,y)
end;
readln;
begline;
start2(t0,t,y0,y);
top(ymin,ymax,t0,tk,shg,hi,bx,by);
while t<=tk do
begin
Eu(g,k1,k2,k3,k4,k6,t1,t2,t3,t4,d,t,h,m,y0,F,y,Gr);
draw(Gr,t,shg,hi,bx,by,h);
end;
finish(t0,tk,ymin,ymax,shg,hi,bx,by);
readln
end.
2.2 . Модуль
unit MDD;
interface {описание структуры программы}
usesgraph;
const m=5;
m2=5;
type mass=array [1..m] of real; {массивдифференциалов}
mass2=array [1..m2] of real; {массивпереходныхпроцессов}
var
y0, y, F: Mass;
Gr: Mass2;
f1,e: text;
i,grdriver,grmode:integer;
g,n,u4,k3,k4,t1,t2,t3,T4,T5,d,k6,k1,k2,h,ymin,ymax,t0,tk,t, shg,hi,bx,by,i1:real;
s:string[8];
procedure start (var ymin, ymax,t0, tk, t,k1,k2,k3,k4,t1,t2, t3,h,g:real;var y0,y:mass);
procedure start2 (var t0,t: real; var y0,y: mass);Procedure Eu (var g,k1, k2,k3,k4,t1,t2,t3, u4, k, d, t, h: real; m:integer; var y0, F, y: mass; var Gr: mass2);
Procedure R (var y0, F: mass; g,k1,k2,k3,k4,k6,t1,t2,t3,t4,n: real);
procedure graphiks (var Gr: mass2; y, y0: mass; g,k1,k2,k3,k4,k6,T1,T2,T3,T4,n: real);
procedure begline;
procedure abc (Gr: mass2; var ymin,ymax:real);
procedure top (ymin,ymax,t0,tk: real; var shg,hi,bx,by: real);
procedure draw (Gr: mass2; t,shg,hi,bx,by,h: real);
procedure finish (t0,tk,ymin,ymax,shg,hi,bx,by: real);
procedure output1;
procedure output (t: real; y: mass);
implementation
procedure start (var ymin,ymax,t0,tk,t,k1,k2,k3,k4,t1,t2,t3,h,g:real;var y0,y:mass); {начальныеприсвоения}
begin
assign (f1, 'C:\nu.txt');
assign (e, 'C:\Result.txt');
reset (f1);
readln(f1);
![]() readln(f1);
readln(f1);
readln(f1,s, T0);
readln(f1,s, TK);
readln(f1,s, h);
read(f1,s);
for i:=1 to m do begin
read(f1, y0[i]);
y[i]:=y0[i];
end;
readln(f1);
readln(f1, s, t1, t2, t3, t4, t5);
readln(f1,s, k1, k2, k3, k4, k6);
readln(f1,s, g);
readln(f1,s, n);
ymin:=y0[1];
ymax:=y0[1];
T:=t0;
close(f1);
end;
procedure start2
(var t0,t: real; var y0,y: mass);
{начальныеприсвоения2}
begin
reset (f1);
readln(f1);
readln(f1);
readln(f1);
readln(f1);
readln(f1);
read(f1,s);
for i:=1 to m do begin
read(f1, y0[i]);
y[i]:=y0[i];
end;
close(f1);
T:=t0;
end;
Procedure Eu (varg,k1, k2,k3,k4,t1,t2,t3, u4, k, d, t, h: real; m:integer; vary0, F, y: mass; varGr: mass2);
 var i: integer;
var i: integer;
begin
R (y0,F,g,k1,k2,k3,k4,k6,T1,T2,T3,T4,n);
for i:=1 to m do for i:=1 to m do
y[i]:=y0[i]+h*F[i];
graphiks(Gr,y,y0,g,k1,k2,k3,k4,k6,T1,T2,T3,T4,n);
t:=t+h;
for i:=1 to m do
y0[i]:=y[i];
end;
Procedure R (var y0, F: mass; g,k1,k2,k3,k4,k6,T1,T2,T3,T4,n: real);
begin
 F[1]:=((g-y0[2]*k6-y0[1])*k2)/T2;
F[1]:=((g-y0[2]*k6-y0[1])*k2)/T2;
F[2]:=y0[5];
F[3]:=(k3*(y0[1]+y0[2])-y0[3])/T3;
F[4]:=(k4*y0[1]-y0[4])/T4;
F[5]:=(y0[4]-2*n*T5*y0[5]-y0[2])/(T5*T5);
end;
procedure graphiks (varGr: mass2; y, y0: mass; g,k1,k2,k3,k4,k6,T1,T2,T3,T4,n: real);
 begin
begin
Gr[1]:=g-k6*y[2];
Gr[2]:=(g-y[2]*k6y[1])*k2+k1*(g-y[2]*k6);
Gr[3]:=y[3];
Gr[4]:=y[2];
Gr[5]:=y[2]*k6;
end;
procedure begline;
begin
grdriver:=detect;
initgraph(grdriver, grmode, 'd:\bp\bgi');
 setfillstyle(1,11);
setfillstyle(1,11);
bar(0,0,640,480);
setcolor(15);
rectangle(40,460,600,40);
i:=40;
while i<600 do
begin
setcolor(15);
line(i,40,i,460);
i:=i+56;
end;
i:=40;
while i<460 do
begin
line(40,i,600,i);
i:=i+42
end;
end;
procedure abc (Gr: mass2; var ymin,ymax: real);
 begin
begin
for i:=1 to m2 do begin
if ymin>Gr[i] then ymin:=Gr[i];
if ymax<Gr[i] then ymax:=Gr[i];
end;
end;
procedure top (ymin,ymax,t0,tk: real; var shg,hi,bx,by: real);
 begin
begin
shg:=560/(tk-t0);
hi:=420/(ymax-ymin);
bx:=600-tk*shg;
by:=440-ymax*hi;
end;
procedure draw (Gr: mass2; t,shg,hi,bx,by,h: real);
{процедурапостроенияграфиков}
begin
for i:=1 to m2 do begin
moveto(round((t-h)*shg+bx),round(GetMaxY-Gr[i]*hi-by));
SetColor(11+i);
SetLineStyle(0,1,3);
lineto(trunc(t*shg+bx),trunc(GetMaxY-Gr[i]*hi-by));
end;
end;
procedure finish (t0,tk,ymin,ymax,shg,hi,bx,by: real);
begin
setfillstyle(1,11);
bar(40,475,600,461);
setfillstyle(1,11);
bar(40,5,635,39);
setfillstyle(1,15);
setcolor(12);
SetLineStyle(0,1,3);
setcolor(5);
i1:=t0;
while i1<=tk do
begin
str(i1:5:2,s);
settextstyle(0,0,1);
outtextxy(round(i1*shg+bx)-10,GetMaxY-30,s);
i1:=i1+(tk-t0)/10;
end;
setcolor(12);
line(50,30,60,30);
settextstyle(0,0,2);
outtextxy(70,20,'E');
setcolor(13);
line(170,30,180,30);
outtextxy(190,20,'U');
setcolor(14);
line(280,30,290,30);
outtextxy(300,20,'A');
setcolor(15);
line(390,30,400,30);
outtextxy(410,20,'Y');
setcolor(16);
line(500,30,510,30);
outtextxy(520,20,'Z');
setcolor(4);
settextstyle(1,0,2);
outtextxy(round(i1*shg+10),getMaxY-40,'T(c)');
setcolor(5);
i1:=ymin;
while i1<=ymax do
begin
str(i1:5:3,s);
settextstyle(0,0,1);
outtextxy(10,round(GetMaxY-i1*hi-by),s);
i1:=i1+(ymax-ymin)/10;
end;
setfillstyle(1,1);
bar(0,0,5,480);
bar(0,0,640,5);
bar(640,0,635,480);
bar(640,480,5,475);
end;
Procedure output1;
begin
rewrite(e);
writeln(e,' Результаты решение системы ДУ');
writeln(e,'****************************************************');
writeln(e,'* T (c) * D(z1) * D(x5) * D(A) * D(x4) * D(x6) *');
writeln(e,'***************************************************');
writeln(' Результаты решение системы ДУ');
writeln('*****************************************************');
writeln('* T (c) * D(z1) * D(x5) * D(A) * D(x4) * D(x6) *');
writeln('*****************************************************');
end;
procedure output (t: real; y: mass); {Вывод на экран результатов решения системы уравнений и их запись во внешний файл}
begin
write (e, t:3:2,' ');
write (t:3:2,' ');
for i:=1 to m do begin write (e, y[i]:5:4,' ');
write (y[i]:5:4,' '); end;
writeln(e);
writeln
end;
END.
3. Графики переходных процессов
Зависимость сигнала на выходе УУП от времени

Зависимость сигнала рассогласования от времени

Зависимость от времени координаты исполнительного органа ИУ

Регулируемая величина

График сигнала обратной связи

Общий вид решения
