Реферат: Штучні нейронні мережі

Реферат

Штучні нейронні мережі

Вступ

Про роботу мозку в даний час відомо дуже мало, тому штучні нейронні мережі (neural networks) є надзвичайно спрощеною моделлю біологічних нейронних мереж. Особливістю нейромереж (neuronet) є те, що вони навчаються, а не програмуються.

1. Біологічні нейронні мережі

Нервова система людини побудована з елементів (нейронів), має приголомшуючу складність. Близько 10¹¹ нейронів беруть участь в приблизно 10¹⁵ передаючих зв'язках, що мають довжину метр і більше. Кожен нейрон володіє багатьма якостями, спільними з іншими елементами тіла, але його унікальною здатністю є прийом, обробка і передача електрохімічних сигналів по нервових шляхах, які утворюють комунікаційну систему мозку.

Рис.1. Біологічний нейрон

На рис. 1 показана структура пари типових біологічних нейронів. Дендрити (входи нейрона) йдуть від тіла нервової клітини до інших нейронів, де вони приймають сигнали в точках з'єднання (синапсах). Прийняті синапсом вхідні сигнали підводяться до тіла нейрона. Тут вони підсумовуються, причому одні входи стимулюють активізацію нейрона, а інші – зниження його активності. Коли сумарна активність (збудження) нейрона перевищує деякий поріг, нейрон переходить в активний стан, посилаючи по аксону (виходу нейрона) сигнал іншим нейронам. У цієї основної функціональної схеми багато спрощень і виключень, проте більшість штучних нейронних мереж моделює лише ці прості властивості.

2. Штучний нейрон

Основними компонентами нейромережі є нейрони /neurons/ (елементи, вузли), які з’єднані зв’язками. Сигнали передаються по зваженим зв’язкам (connection), з кожним з яких пов’язаний ваговий коефіцієнт (weighting coefficient) або вага.

Моделі НМ – програмні і апаратні, найбільш поширені – програмні.

Використання – розпізнавання образів, прогнозування, створення асоціативної пам’яті.

Штучний нейрон імітує в першому наближенні властивості біологічного нейрона. На вхід штучного нейрона поступає множина сигналів, які є виходами інших нейронів. Кожен вхід множиться на відповідну вагу, аналогічну його синаптичній силі, і всі виходи підсумовуються, визначаючи рівень активації нейрона. На рис.2 представлена модель, що реалізує цю ідею. Хоча мережеві парадигми досить різноманітні, в основі майже всіх їх лежить ця конфігурація. Тут множина вхідних сигналів, позначених x₁ , x₂ ,…, x_n , поступає на штучний нейрон. Ці вхідні сигнали, в сукупності позначаються вектором X, відповідають сигналам, що приходять в синапси біологічного нейрона. Кожен сигнал множиться на відповідну вагу w₁ , w₂ ,…, w_n , і поступає сумуючий блок, позначений Σ. Кожна вага відповідає «силі» одного біологічного синаптичного зв'язку (множина ваг в сукупності позначається вектором W). Сумуючий блок, який відповідає тілу біологічного нейрона, складає зважені входи алгебраїчно, створюючи вихід, який ми називатимемо NET. У векторних позначеннях це може бути компактно записано таким чином

NET = XW.

Рис.2. Штучний нейрон

3. Активіаційні функції

Сигнал NET далі, як правило, перетворюється активаційною функцією F і дає вихідний нейронний сигнал OUT = F(NET). Активаційна функція F(NET) може бути:

1. Пороговою бінарною функцією (рис.3а)

,

де Т - деяка постійна порогова величина, або ж функція, що точніше моделює нелінійну передавальну характеристику біологічного нейрона.

2. Лінійною обмеженою функцією (рис.3б)

.

Функцією гіперболічного тангенса (рис.3в)

.

де С > 0 – коефіцієнт ширини сигмоїди по осі абсцис (звичайно С=1).

4. Сигмоїдною (S-подібною) або логістичною функцією (рис.3г)

,

З виразу для сигмоїда очевидно, що вихідне значення нейрона лежить в діапазоні [0,1] (рис.4). Популярність сигмоїдної функції зумовлюють наступні її властивості:

· здатність підсилювати слабкі сигнали сильніше, ніж великі, і опиратися „насиченню” від потужних сигналів;

· монотонність і диференційованість на всій осі абсцис;

· простий вираз для похідної

,

що дає можливість використовувати широкий спектр оптимізаційних алгоритмів.

В штучному нейроні з активізаційною функцією (рис.5) блок, позначений F, приймає сигнал NET і видає сигнал OUT. Якщо блок F звужує діапазон зміни величини NET так, що при будь-яких значеннях NET значення OUT належать деякому кінцевому інтервалу, то F називається «стискаючою» функцією. Як «стискаюча» функція часто використовується сигмоїдна функція.

а) б)

в) г)

Рис. Вид функцій активації: а) порогова бінарна функція; б) лінійна обмежена функція; в) гиперболічний тангенс; г) сигмоїд

Рис.4. Сигмоїдальна активіаційна функція для С=1

Рис.5. Штучний нейрон з активіаційною функцією F

4. Одношарові нейронні мережі

Хоча один нейрон і здатний виконувати прості процедури розпізнавання, сила нейронних обчислень виникає від з'єднань нейронів в мережах. Проста мережа складається з групи нейронів, створюючих шар, як показано в правій частині рис.6. Відзначимо, що вершини-круги зліва служать лише для розподілу вхідних сигналів. Вони не виконують будь-яких обчислень, і тому не вважатимуться шаром. З цієї причини вони позначені кругами, щоб відрізняти їх від обчислюючих нейронів, позначених квадратами. Кожен елемент з множини входів Х окремою вагою сполучений з кожним штучним нейроном. Кожен нейрон видає зважену суму входів в мережу. У штучних і біологічних мережах багато з'єднань можуть бути відсутніми, можуть мати місце також з'єднання між виходами і входами елементів в шарі.

Рис.6. Одношарова НМ

Зручно вважати вагу елементами матриці W. Матриця має m рядків і n стовпців, де m - число входів, а n - число нейронів. Наприклад, w_3,2 - це вага, що пов'язує третій вхід з другим нейроном. Таким чином, обчислення вихідного вектора Y, компонентами якого є виходи OUT нейронів, зводиться до матричного множення Y = XW, де Y і Х - вектори-рядки.

5. Персептрони і зародження штучних нейромереж

Як науковий предмет штучні нейронні мережі вперше заявили про себе в 40-ві роки. Прагнучи відтворити функції людського мозку, дослідники створили прості апаратні (а пізніше програмні) моделі біологічного нейрона і системи його з'єднань. Коли нейрофізіологи досягли глибшого розуміння нервової системи людини, ці ранні спроби стали сприйматися як досить грубі апроксимації. Проте на цьому шляху були досягнуті вражаючі результати, що стимулювали подальші дослідження, що привели до створення досконаліших мереж.

Перше систематичне вивчення штучних нейронних мереж було зроблене Мак-Каллоком і Піттсом в 1943 р.. В роботі вони досліджували мережеві парадигми для розпізнавання зображень, що піддаються зсувам і поворотам. Проста нейронна модель, показана на рис.7, використовувалася в більшій частині їх роботи. Елемент Σ множить кожен вхід х на вагу w і підсумовує зважені входи. Якщо ця сума більше заданого порогового значення, вихід рівний одиниці, інакше - нулю. Ці системи (і множина ним подібних) одержали назву персептронів. Вони складаються з одного шару штучних нейронів, сполучених за допомогою вагових коефіцієнтів з множиною входів (рис.8), хоча описуються і складніші системи.

Рис.7. Нейрон персептрона

Перші персептрони були створені Ф.Розенблатом у 60-х роках і викликали великий інтерес. Первинна ейфорія змінилася розчаруванням, коли виявилося, що персептрони не здатні навчитися рішенню ряду простих задач. М.Мінський строго проаналізував цю проблему і показав, що є жорсткі обмеження на те, що можуть виконувати одношарові персептрони, і, отже, на те, чому вони можуть навчатися. Оскільки у той час методи навчання багатошарових мереж не були відомі, дослідники перейшли в більш багатообіцяючі області, і дослідження у області нейронних мереж прийшли в занепад. Відкриття методів навчання багатошарових мереж більшою мірою, ніж який-небудь інший чинник, вплинуло на відродження інтересу і дослідницьких зусиль.

Рис.8. Персептрон

Навчання персептрона:

1. Ініціалізація вагових матриць W (випадкові значення)

2. Подати вхідX і обчислити вихід Y для цільового вектора Y^T

3. Якщо вихід правильний – перейти на крок 4; інакше обчислити різницю D = Y^T – Y; модифікувати ваги за формулою:

w_ij (e+1) = w_ij (e) + α D Х_і ,

де w_ij (e) - значення ваги від нейрона i до нейрона j до налагодження, w_ij (e+1) - значення ваги після налагодження, α - коефіцієнт швидкості навчання, Х_i - вхід нейрона i, e – номер епохи (ітерації під час навчання).

4. Виконувати цикл з кроку 2, поки мережа не перестане помилятися. На другому кроці у випадковому порядку пред’являються всі вхідні вектори.

Один з найпесимістичніших результатів Мінського показує, що одношаровий персептрон не може відтворити таку просту функцію, як ВИКЛЮЧАЄ АБО. Це функція від двох аргументів, кожний з яких може бути нулем або одиницею. Вона приймає значення одиниці, коли один з аргументів рівний одиниці (але не обидва).

6. Багатошарові нейронні мережі

Багатошарові мережі (рис.9) володіють значно більшими можливостями, ніж одношарові. Проте багатошарові мережі можуть привести до збільшення обчислювальної потужності в порівнянні з одношаровими лише в тому випадку, якщо активаційна функція між шарами буде нелінійною. Обчислення виходу шару полягає в множенні вхідного вектора на першу вагову матрицю з подальшим множенням (якщо відсутня нелінійна активаційна функція) результуючого вектора на другу вагову матрицю (XW₁ )W₂ . Оскільки множення матриць асоціативне, то X(W₁ W₂ ). Це показує, що двошарова лінійна мережа еквівалентна одному шару з ваговою матрицею, рівною добутку двох вагових матриць. Отже, для лінійної активіаційної функції будь-яка багатошарова лінійна мережа може бути замінена еквівалентною одношаровою мережею.

Рис.9. Багатошарова НМ

7. Навчання нейронних мереж

Мережа навчається, щоб для деякої множини входів Xдавати бажану множину виходівY. Кожна така вхідна (або вихідна) множина розглядається як вектор. Навчання здійснюється шляхом послідовного пред'явлення вхідних векторів з одночасним налагодженням ваг відповідно до певної процедури. В процесі навчання ваги мережі поступово стають такими, щоб кожен вхідний вектор виробляв вихідний вектор. Розрізняють алгоритми навчання з вчителем і без вчителя, детерміновані і стохастичні.

Навчання з вчителем. Навчання з вчителем припускає, що для кожного вхідного вектора Xіснує цільовий вектор Y^T , що є необхідним виходом. Разом вони називаються навчальною парою. Звичайно мережа навчається для деякої кількості таких навчальних пар (навчальної множини). В ході навчання зчитується вхідний вектор X, обчислюється вихід мережі Y і порівнюється з відповідним цільовим вектором Y^T , різниця D ~ Y^T – Yза допомогою зворотного зв'язку подається в мережу і змінюються ваги Wвідповідно до алгоритму, прагнучого мінімізувати помилку ε. Зчитування векторів навчальної множини і налагодження ваг виконується до тих пір, поки сумарна помилка для всієї навчальної множини не досягне заданого низького рівня.

Навчання без вчителя

Не зважаючи на численні прикладні досягнення, навчання з вчителем критикувалося за свою біологічну неправдоподібність. Важко уявити навчальний механізм в мозку, який би порівнював бажані і дійсні значення виходів, виконуючи корекцію за допомогою зворотного зв'язку. Якщо допустити подібний механізм в мозку, то звідки тоді виникають бажані виходи? Навчання без вчителя є набагато правдоподібнішою моделлю навчання в біологічній системі. Розвинена Кохоненом і багатьма іншими, вона не потребує цільового вектора для виходів і, отже, не вимагає порівняння з ідеальними відповідями. Навчальна множина складається лише з вхідних векторів. Навчальний алгоритм налагоджує вагу мережі так, щоб виходили узгоджені вихідні вектори, тобто щоб пред'явлення досить близьких вхідних векторів давало однакові виходи. Процес навчання виділяє статистичні властивості навчальної множини і групує схожі вектори в класи.

Алгоритми навчання

Більшість сучасних алгоритмів навчання виросла з концепцій Хебба. Ним запропонована модель навчання без вчителя, в якій синаптична сила (вага) зростає, якщо активовані обидва нейрони, джерело і приймач. Таким чином, часто використовувані шляхи в мережі посилюються і феномен звички і навчання через повторення одержує пояснення.

У штучній нейронній мережі, що використовує навчання по Хеббу, нарощування ваг визначається добутком рівнів збудження передаючого і приймаючого нейронів. Це можна записати як

w_ij (e+1) = w(e) + α OUT_i OUT_j ,

де w_ij (e) - значення ваги від нейрона i до нейрона j до налагодження, w_ij (e+1) - значення ваги від нейрона i до нейрона j після налагодження, α - коефіцієнт швидкості навчання, OUT_i - вихід нейрона i та вхід нейрона j, OUT_j - вихід нейрона j; e – номер епохи (ітерації під час навчання).

Для навчання нейромереж в багатьох випадках використовують алгоритм зворотного розповсюдження помилки. Розв’язок задачі за допомогою нейронної мережі зводиться до наступних етапів:

1. Вибрати відповідну модель мережі (наприклад, трьохшарову )

2. Визначити топологію мережі (кількість елементів та їх зв’язки)

3. Вказати спосіб навчання (наприклад, зі зворотним розповсюдженням помилок) і параметри навчання

Кількість прихованих елементів – не менша за кількість вхідних.

8. Алгоритм зворотного розповсюдження помилки (backpropagation)

Зворотне розповсюдження помилки означає, що сигнали помилки з виходу мережі використовуються для корекції ваг попередніх шарів.

Розглянемо структуру 3-шарової нейромережі.

1. Вхідний шар X; стани його елементів записані у векторі vX_i ; де i=1..Q_X . Розмір навчальної множини (кількість векторів) на вході Х дорівнює Qn, номер вектора n=1..Q_N .

2. Приховані шари

Шар V¹ (рівень L=1): вектор V¹ _{k 1} ; де k₁ =1..Q_{V 1} ; матриця ваг W¹ _{i , k 1} ; різниця векторів D¹ _{k 1} ; Шар V² (L=2): вектор V² _{k 2} ; де k₂ =1..Q_{V 2} ; матриця ваг W² _{k 1, k 2} ; різниця D² _{k 2} ; Вихідний шар (L=3): стани його елементів записані у векторі Y_j ; j=1..Q_Y ; матриця ваг W³ _{k 2, j} ; різниця D³ _j ; істинний вихід (true) описується вектором Y^T _j ; j=1..Q_Y .

Тобто Y^t _j – істинне значення для елементу j, Y_j - його реальних вихід.

Розмір навчальної вибірки на виході Y: Q_M , номер вектора m=1..Q_M .

Навчання нейромережі відбувається за наступним алгоритмом (рис.10)

Рис.10. Алгоритм навчання нейромережі зі зворотним розповсюдженням помилки

1. Ініціалізація. Початкові вагові коефіцієнти W приймаються рівними малим випадковим значенням, наприклад з діапазону [-0.3, .... +0.3]:

, ΔW=0,

У вагових матрицях рядки відповідають елементам, від яких йдуть зв’язки, а стовпці – до яких йдуть зв’язки.

2. Нормалізація (масштабування) значень всіх векторів X, Y^Т (для кожного типу окремо) в діапазон (MinN; MaxN), наприклад MinN=0,1; MaxN=0,9;

Пряме розповсюдження (Direct) полягає у знаходженні вихідного вектора Yна основі вхідного Xза наступними формулами.

Шар 1:

; , де

Шар 2:

; , де

Шар 3:

; , де

В результаті прямого розповсюдження можна обчислити помилки навчання мережі:

- лінійна помилка для вектора n

- лінійна помилка для всіх векторів навчальної множини

- сумарна квадратична помилка (для всіх векторів)

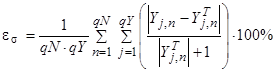- середня відносна помилка (0 – 100%)

Якщо значення сумарної квадратичної помилки ε_k менше заданого, то процес навчання мережі завершується.

4. Зворотнє розповсюдження помилки (backpropagation) полягає у корекції вагових коефіцієнтів через сигнал різниці D.

3 шар

, ,

де , e - номер епохи; оскільки в якості активіаційної функції використовується сигмоїдна, тому різниця векторів (Y^T -Y) множиться на похідну від сигмоїдної функції: Y(1 – Y) .

2 шар

, ,де

1 шар

, , де ,

η_Y , η_{L 2} , η_{L 1} - норми навчання (значення норми навчання, наприклад, 0,5).

З метою контролю процесу навчання мережі для матриці W визначаються:

Min – мінімальне значення;

Max – максимальне;

Ms – математичне сподівання;

Sigma – середньоквадратичне відхилення

Дані для нейронної мережі можна поділити наступним чином:

1. Навчання (відомі вхідні і вихідні дані, визначити вагові коефіцієнти)

2. Тестування (відомі вхідні і вихідні дані, порівняти розраховані вихідні дані з істинними)

3. Діагностика (реальне визначення результатів за вхідними даними)

9. Мережі зустрічного розповсюдження. Шари Кохонена і Гроссберга

Основною перевагою НМ зустрічного розповсюдження є порівняно малий час навчання (приблизно в 100 разів менше, ніж для зворотного розповсюдження помилки). В зустрічному розповсюдженні об'єднані два добре відомих алгоритми: карта Кохонена і зірка Гроссберга.

Мережа зустрічного розповсюдження функціонує подібно до довідкового бюро. В процесі навчання вхідні вектори асоціюються з відповідними вихідними векторами. Ці вектори можуть бути двійковими або неперервними. Коли мережа навчена, обробка вхідного вектора приводить до необхідного вихідного вектора. Узагальнююча здатність мережі дозволяє одержувати правильний вихід навіть при пошкодженого вхідного вектора. Це дозволяє використовувати дану мережу для розпізнавання і відновлення образів.

Структура НМ зустрічного розповсюдження наступна (рис.11)

Рис.11. НМ зустрічного розповсюдження без зворотних зв’язків

Нейрони шару 0 (круги) служать лише точками розгалуження і не виконують обчислень. Кожен нейрон шару 0 сполучений з кожним нейроном шару 1 (шару Кохонена) окремою вагою w_mn . Ця вага в цілому розглядається як матриця ваг W. Аналогічно, кожен нейрон в шарі Кохонена (шарі 1) сполучений з кожним нейроном в шарі Гроссберга (шарі 2) вагою v_np . Ця вага утворює матрицю ваг V. Зустрічне розповсюдження функціонує в двох режимах: у нормальному режимі, при якому приймається вхідний вектор Х і видається вихідний вектор У, і в режимі навчання, при якому подається вхідний вектор і ваги коректуються, щоб дати необхідний вихідний вектор.

НОРМАЛЬНЕ ФУНКЦІОНУВАННЯ

Шари Кохоненна. У своїй простій формі шар Кохонена функціонує за принципом «переможець забирає все», тобто для даного вхідного вектора один і лише один нейрон Кохонена видає на виході логічну одиницю, всі інші видають нуль. Переможцем є нейрон з максимальним значенням вихідного сигналу .

Вихід нейронів шару Гроссберга є сумою .

НАВЧАННЯ

Шар Кохонена класифікує вхідні вектори в групи схожих. Це досягається за допомогою такого налагодження ваг шару Кохонена, що близькі вхідні вектори активують один і той же нейрон даного шару. Задачею шару Гроссберга є отримання необхідних виходів. Навчання шару Кохонена є самонавчанням, що виконується без вчителя

10. Стохастичні методи

Стохастичні методи корисні як для навчання штучних нейронних мереж, так і для отримання виходу від вже навченої мережі. Стохастичні методи навчання приносять велику користь, дозволяючи виключати локальні мінімуми в процесі навчання. Проте з ними також зв'язаний ряд проблем. Штучна нейронна мережа навчається за допомогою деякого процесу, що модифікує її вагу. Якщо навчання успішне, то пред'явлення мережі множини вхідних сигналів приводить до появи бажаної множини вихідних сигналів. Є два класи повчальних методів: детерміністичний і стохастичний.

Детерміністичний метод навчання крок за кроком здійснює процедуру корекції ваг мережі, засновану на використанні їх поточних значень, а також величин входів, фактичних виходів і бажаних виходів. Зворотне розповсюдження помилки є прикладом подібного підходу.

Стохастичні методи навчання виконують псевдовипадкові зміни величин ваг, зберігаючи ті зміни, які ведуть до поліпшень. Для навчання мережі може бути використана наступна процедура:

1. Вибрати вагу випадковим чином і змінити її на невелику випадкову величину. Пред'явити множину входів і обчислити виходи.

2. Порівняти виходи з бажаними виходами і обчислити величину різниці між ними. Загальноприйнятий метод полягає в знаходженні різниці між фактичним і бажаним виходами для кожного елементу навчаної пари. Метою навчання є мінімізація цієї різниці (цільової функції).

3. Якщо зміна ваги допомагає (зменшує цільову функцію), то зберегти її, інакше повернутися до первинного значення ваги.

Повторювати кроки з 1 до 3 до тих пір, поки мережа не буде навчена достатньою мірою.

Однією з найбільших проблем при навчанні НМ є локальні мінімуми (рис.12).

Рис.12. Проблема локальних мінімумів

Для вирішення проблеми локальних мінімумів використовується наступний метод. Штучні нейронні мережі навчаються спочатку грубим налагодженням ваг, а потім більш точним. На першому етапі робляться великі випадкові корекції із збереженням тільки тих змін ваг, які зменшують цільову функцію. Потім середній розмір кроку поступово зменшується, і глобальний мінімум досягається. Це нагадує відпал металу, тому для опису такої методики використовують термін «імітація відпалу». У металі, нагрітому до температури, що перевищує його точку плавлення, атоми знаходяться в сильному безладному русі. Як і у всіх фізичних системах, атоми прагнуть до стану мінімуму енергії (єдиному кристалу в даному випадку), але при високих температурах енергія атомних рухів перешкоджає цьому. В процесі поступового охолоджування металу виникають все більш низькоенергетичні стани, поки не буде досягнуто глобальний мінімум. В процесі відпалу розподіл енергетичних рівнів описується наступним співвідношенням (розподілом Больцмана):

P(e)= exp(-е/kT)

де Р(е) – ймовірність того, що система знаходиться в стані з енергією е; k - постійна Больцмана; Т - температура за шкалою Кельвіна.

При високих температурах Р(е) наближається до одиниці для всіх енергетичних станів. У міру зменшення температури ймовірність високоенергетичних станів зменшується в порівнянні з низькоенергетичними.У випадку НМ Р(е) – ймовірність того, що буде збережена зміна ваги, яка приводить до збільшення цільвої функції.

11. Мережі зі зворотними зв’язками, мережі Хопфілда

Одними із НМ зі зворотними зв’язками є мережі Хопфілда.

Мережі зі зворотними зв'язками мають шляхи, що передають сигнали від виходів до входів, тому відгук таких мереж є динамічним, тобто після зчитування нового входу обчислюється вихід і, передаючись по мережі зворотного зв'язку, модифікує вхід. Потім вихід повторно обчислюється, і процес повторюється знову і знову. Для стійкої мережі послідовні ітерації приводять до все менших змін виходу, поки вихід не стає постійним. Для багатьох мереж процес ніколи не закінчується, такі мережі називають нестійкими. Нестійкі мережі володіють цікавими властивостями і вивчалися як приклад хаотичних систем.

Розглянемо мережу зі зворотними зв’язками, яка містить 1 шар

Рис.13 Одношарова НМ зі зворотними зв’язками. Пунктирні лінії позначають нульові ваги.

В першій роботі Хопфілда функція F була просто пороговою відносно порогу T. Вона обчислюється наступним чином:

,

OUT= 1, якщо NET_j >Т_j ,

OUT = 0, якщо NET_j <Т_j ,

OUT не змінюються, якщо NET_j = Т_j ,

Мережа з зворотними зв’язками є стійкою, якщо її матриця симетрична й має нулі на головній діагоналі, тобто якщо w_ij = w_ji й w_ii = 0 для всіх i.

Людська пам'ять асоціативна, тобто деякий спогад може породжувати велику пов'язану з ним область. Наприклад, декілька музичних тактів можуть викликати цілу гамму спогадів, включаючи пейзажі, звуки і запахи. Навпаки, звичайна комп'ютерна пам'ять адресується локально.

Мережа із зворотним зв'язком формує асоціативну пам'ять. Подібно людській пам'яті по заданій частині потрібної інформації вся інформація витягується з «пам'яті». Щоб організувати асоціативну пам'ять за допомогою мережі із зворотними зв'язками, вага повинна вибиратися так, щоб утворювати енергетичні мінімуми в потрібних вершинах одиничного гіперкуба.

Хопфілд розробив асоціативну пам'ять з безперервними виходами, що змінюються в межах від +1 до -1, відповідних двійковим значенням 0 і 1. Інформація, що запам'ятовується, кодується двійковими векторами і зберігається у вагах згідно наступній формулі:

де m - число вихідних векторів, що запам'ятовуються; d - номер вихідного вектора, що запам'ятовується; OUT_i,j - i-компоненту вихідного вектора, що запам'ятовується.

12. Адаптивна резонансна теорія

Мозок людини виконує важку задачу обробки безперервного потоку сенсорної інформації, одержуваної з навколишнього світу. З потоку тривіальної інформації він повинен виділити життєво важливу інформацію, обробити її і, можливо, зареєструвати в довготривалій пам'яті. Розуміння процесу людської пам'яті є серйозною проблемою; нові образи запам'ятовуються в такій формі, що раніше запам'ятовані не модифікуються і не забуваються. Це створює дилему: яким чином пам'ять залишається пластичною, здібною до сприйняття нових образів, і в той же час зберігає стабільність, що гарантує, що образи не знищаться і не руйнуватимуться в процесі функціонування?

Традиційні штучні нейронні мережі виявилися не в змозі розв'язати проблему стабільності-пластичності. Дуже часто навчання новому образу знищує або змінює результати попереднього навчання. В деяких випадках це не істотно. Якщо є тільки фіксований набір повчальних векторів, вони можуть пред'являтися при навчанні циклічно. У мережах із зворотним розповсюдженням, наприклад, навчальні вектори подаються на вхід мережі послідовно до тих пір, поки мережа не навчиться всьому вхідному набору. Якщо, проте, повністю навчена мережа повинна запам'ятати новий повчальний вектор, він може змінити вагу настільки, що потрібно повне перенавчання мережі.

У реальній ситуації мережа піддаватиметься діям, що постійно змінюються; вона може ніколи не побачити один і той же навчальний вектор двічі. При таких обставинах мережа часто не навчатиметься; вона безперервно змінюватиме свою вагу, не досягаючи задовільних результатів.

Більш того, в роботі є приклади мережі, в якій тільки чотири повчальні вектори, що пред'являються циклічно, примушують ваги мережі змінюватися безперервно, ніколи не сходячись. Така нестабільність є одним з головних чинників, що примусили Гроссберга і його співробітників досліджувати радикально відмінні конфігурації. Адаптивна резонансна теорія (APT) є одним з результатів дослідження цієї проблеми.

Мережею APT є векторний класифікатор. Вхідний вектор класифікується залежно від того, на якій з множини образів, раніше запам'ятованих, він схожий. Своє класифікаційне рішення мережа APT виражає у формі збудження одного з нейронів шару, що розпізнає. Якщо вхідний вектор не відповідає жодному з образів, що запам'ятовані, то створюється нова категорія. Якщо визначено, що вхідний вектор схожий на один із запам’ятованих векторів (для певного критерію схожості), то запам’ятований вектор буде змінюватиметься під впливом нового вхідного вектора так, щоб стати більш схожим на цей вхідний вектор.

Таким чином розв'язується дилема стабільності-пластичності. Новий образ може створювати додаткові класифікаційні категорії, проте новий вхідний образ не може примусити змінитися існуючу пам'ять.