Курсовая работа: Компьютерные 2d и 3d иллюстрации свойств геометрических фигур и тел при изучении геометрии в шко

Введение

В условиях модернизации системы образования повышаются требования как к качеству подготовки выпускника школы, так и к эффективности образовательной деятельности в целом. Одним из направлений реализации этих положений является процесс информатизации образования, предполагающий внедрение новых информационных технологий в эту область деятельности. Отмечая в целом значительный вклад ИКТ в школьное образование и подготовку будущих учителей математики, остановимся более подробно на изменениях в учебном процессе, обусловленных применением 2D и 3D графики.

При традиционном подходе к изучению курса стереометрии (без использования компьютера) учащийся, получивший только неполное среднее образование практически незнаком с этим разделом геометрии. Здесь, по-моему мнению, возможны два пути изменения ситуации. Первый заключается в воплощении идей Ф. Клейна путем реализации фузионистского (сочетание в одном курсе элементов планиметрии и стереометрии)подхода в обучении геометрии. И второй путь, близкий первому, – более смелое использование элементов стереометрии (понятий, моделей) на уроках уже в 7-9х классах. Причем реализация обоих подходов наиболее эффективна с применением различных графических пакетов и предметно-ориентированного программирования.

Использование 2D и 3D графики привносит ряд изменений не только в структуру курса геометрии, но и в содержание учебного материала. Так до недавнего времени понятие «фрактал» было знакомо лишь узкому кругу специалистов. Однако, на XIV Международной конференции «Математика. Компьютер. Образование» в своем докладе «Современное образование и глобальные проблемы» Н. Х. Розов отметил, что настало время «осовременить» школьный курс геометрии, в частности, с помощью простейших геометрических примеров ввести понятие «фрактал». Тем более что современные компьютерные технологии позволяют создавать программы, демонстрирующие графическое изображение фрактальных структур.

2D и 3D графика вносит ряд изменений и в методы обучения. Например, можно совершенствовать метод моделирования геометрических тел, создавая виртуальные модели. В силу сложности строения изучаемых объектов (звездчатые многогранники, «седло») зачастую отсутствует возможность создать их материальную модель. Решение этой проблемы авторы видят в использовании компьютерной графики. Изучение 4-мерных геометрических тел затруднительно в силу отсутствия возможности работать с их материальными моделями. Но становится возможным представить их по проекциям на гиперплоскость, демонстрируемым компьютерной программой. С помощью этой программы очень красиво может быть решена задача 4-мерного куба.

Крайне редко используются 2D и 3D графика в дидактических играх. Однако, при наличии разнообразных изображений игра как организационная форма приобретает новые качества. Например, игра «Лабиринт». Ее игровой замысел: развитие пространственного мышления обучающихся. Игровые действия: участник находится в виртуальном лабиринте (при этом у него нет точки обзора сверху). После прохождения им определенного маршрута участнику требуется восстановить на предложенной двумерной карте его путь. Возможно выполнение задачи, обратной первой.

Рассмотрим некоторые компьютерные разработки, используемые при обучении геометрии. В настоящее время имеет широкое применение проект «открытая математика», содержащий электронный учебник, интерактивный конструктор для решения задач на построение, звуковое сопровождение. С помощью предлагаемого инструментария осуществляется более детальная проработка изучаемого материала . Не менее популярными являются пакеты Mathсad и Maple. Другой полезный графический редактор – 3D STUDIO MAX, приобретающий в последнее время все большую популярность.

Итак, целью работы является разработка трёхмерных иллюстраций свойств геометрических фигур и тел для изучения геометрии в школе.

Для реализации данной цели необходимо решить следующие задачи:

1. Выбрать современный многофункциональный программный продукт, позволяющий создать 3dмодели не только оперативно но и на высоком уровне.

2. Разработать проект так, чтобы он был прост и понятен в использовании.

3. Разработать проект, чтобы он использовал минимальное количество ресурсов и был удобен в эксплуатации.

Глава 1. Основные виды компьютерной графики

Под видами компьютерной графики подразумевается способ хранения и отображения изображения на плоскости монитора. Как и в любом другом искусстве в компьютерной графике есть свои специфические виды графических изображений.

К ним относятся:

1. растровое изображение

2. векторное изображение

3. трехмерное изображение

4. фрактальное изображение

Есть еще и символьное изображение. Но о нем мы говорить не будем, потому что оно устарело. И на сегодняшний день практически не используется. Дизайнеры работают с каждым изображением по-разному, используя различные графические пакеты программ.

Начнем знакомиться с растровой графикой. Надо сказать, что этот вид графики наиболее распространен и связанно это в первую очередь с особенностями восприятия человеком изображения. Свет, отражённый от поверхности предмета проецируется на сетчатку глаза, где он воспринимается миллионами светочувствительными клетками глаза. Происходит кодирование светового сигнала, он разбивается на множество частей, которые в свою очередь попадают в мозг, где и воспринимается как объёмный предмет.

1.1 Растровая графика

Тот же процесс напоминает и растровая графика при демонстрации на мониторе компьютера, только в обратном порядке. Растровая графика напоминает нам лист клетчатой бумаги или шахматную доску, на которой любая клетка закрашивается определенным цветом, образуя (в совокупности) рисунок. Основной элемент растровых изображений точка – она еще называется пиксель. Точка или пиксель – это основной минимальный элемент растрового изображения.

Его мы можем сравнить с одной клеточкой бумаги. Из множества пикселей (клеточек) и состоит растровое компьютерное изображение. А вот Растр – это сетка или матрица, которая состоит из точек (пикселей). Растр имеет очень много различных характеристик, которые фиксируются компьютером. Запомните две важные характеристики: размер и расположение пикселей – характеристики, которые фиксируются компьютером. Файл растровых изображений должен их сохранить, чтобы создать картинку.

Еще одна характеристика - это цвет. Цвет – важная характеристика для растровых изображений. Так, например, изображение описывается конкретным расположением и цветом каждой точки сетки. Вы видели мозаичное панно? Так вот, в растровой графике эти действия похожи на создание изображения в технике мозаики. Более подробно о растровой графике мы поговорим на третьем уроке, который так и называется растровая графика.

1.2 Векторная графика

Чем же интересно векторное изображение, используемое в компьютерной графике? Во-первых, с помощью векторной графики можно решить много художественно - графических задач. Во-вторых, возможность масштабирования векторного изображения без потери качества может быть ценна, например, при создании большой по размеру рекламы. Увеличение или уменьшение объекта производится увеличением или уменьшением соответствующих коэффициентов в математических формулах. Любое векторное изображение можно представить в виде набора векторных объектов, расположенных определенным образом друг относительно друга.

Векторное изображение можно сравнить с аппликацией, состоящей из кусочков цветной бумаги, наклеенных (наложенных) один на другой. Однако, в отличие от аппликации, в векторном изображении легко менять форму и цвет составных частей. Векторный графический объект включает два элемента: контур и его внутреннюю область, которая может быть пустой или иметь заливку в виде цвета, цветового перехода (градиента), или мозаичного рисунка. Контур может быть как замкнутым, так и разомкнутым.

Контур в векторном объекте выполняет двойную функцию. С помощью контура можно менять форму объекта. Контур векторного объекта можно оформлять (тогда он будет играть роль обводки), предварительно задав его цвет, толщину и стиль линии. Именно этот вид изображений в компьютерной графике называют объектно-ориентированным. Почему? А потому, что каждый элемент изображения представляет собой отдельный объект, у которого можно изменить контур, заливку цветом, пропорции.

Возможность редактирования (изменения) контура может применяться при работе над дизайном изделия из стекла, керамики, и, вообще, пластичных материалов. Очень хорошо применять векторное изображение при разработке орнамента (в круге, квадрате, полосе, овале) для украшения декоративного изделия (слайд-шоу из орнаментов). Разработав всего один элемент орнамента, его можно много раз повторить (размножить) без дополнительной прорисовки, сэкономив много времени для другой работы Особенно важно, что векторное изображение изначально позволяет выполнять точные геометрические построения, следовательно, чертежи и другую конструкторскую документацию

К большому сожалению, векторный формат становится невыгодным при передаче изображений с большим количеством оттенков или множеством мелких элементов, например, фотографий. Ведь каждый мельчайший блик в этом случае будет представляться не совокупностью одноцветных точек, а сложнейшей математической формулой или множеством графических элементов (примитивов), каждый из которых, является формулой. Все это приводит к большому файлу. Файлы растровых изображений имеют гораздо больший размер, чем векторные, так как в памяти компьютера каждый из объектов этой графики сохраняется в виде математических уравнений. В то же время как параметры каждой точки в файле растровой графики задаются индивидуально. Вот откуда такие огромные размеры файлов в этой графике.

1.3 Трехмерная графика

Одной из наиболее интересных, в то же время сложных видов изображений в компьютерной графике является трехмерное изображение (или его еще называют – трехмерной графикой). Заметим, что трехмерная графика уходит своими корнями и имеет много общего с векторной компьютерной графикой.

Она также может называться объектно-ориентированной. Это позволяет изменять как все элементы трехмерной сцены, так и каждый объект в отдельности. Применяется она при разработке дизайн-проектов интерьера, архитектурных объектов, в рекламе, при создании обучающих компьютерных программ, видеороликов, наглядных изображений деталей и изделий в машиностроении и т. д. В трехмерной графике изображения (или персонажи) моделируются и перемещаются в виртуальном пространстве, в природной среде или в интерьере, а их анимация позволяет увидеть объект с любой точки зрения, переместить в искусственно созданной среде и пространстве, разумеется, при сопровождении специальных эффектов.

Эти свойства трехмерной графики позволяют создавать и кинопродукцию профессионального качества. Интересно, что в процессе разработки трехмерной графики и ее анимации человек выступает в качестве режиссера и оператора, поскольку ему приходится придумывать сюжет, содержание и композицию каждого кадра и распределять движение объекта или объектов сцены не только в пространстве, но и во времени. Что же требует трехмерная графика от человека? Конечно же, умение моделировать различные формы и конструкции при помощи различных программных средств, а также знания ортогонального (прямоугольного) и центрального проецирования. Последняя - называется перспективой.

1.4 Фрактальное изображение

И последний вид компьютерной графики это фрактальное изображение. Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики. Математической основой фрактальной графики является фрактальная геометрия. В основу метода построения изображений во фрактальной графике положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников. О каждом из представленных видов компьютерной графики будет более подробно рассказано на следующих уроках, а этот урок закончен.

Глава 2. 3 D моделирование

2.1 Представление 3D-моделей

Поскольку современные компьютеры широкого назначения (в первую очередь самый распространенный Intel Pentium в любых его модификациях) наиболее просто реализуют арифметические операции сложения и умножения (деление уже является заметно затратным по времени, а вычисление не только специальных, но и элементарных арифметических функций, таких как квадратный корень, синус, косинус, арктангенс и т.п., даже при их аппаратной реализации в арифметическом сопроцессоре, и тем более), то основным методом моделирования неизбежно остается классический линеаризованный подход. Модели твердых тел соответственно являются локально-линейными, поскольку их поверхность ограничивает некоторую часть 3D-пространства и составлена из полигонов, образованных частями соответствующих 2D-плоскостей, ограниченных лежащими в этих плоскостях замкнутыми ломаными. Другим важным обстоятельством, ограничивающим обработку данных классом линейных методов, является одинаковый вид результатов решения прямых и обратных задач. Таким образом, в качестве базовой единицы представления полигональных твердотельных моделей принят полиэдр (многогранник).

Возможно, однако, некоторое расширение класса геометрических тел, пригодных для эффективного компьютерного моделирования. Так, следующие по сложности объекты второго порядка (шар, цилиндр, конус), математическое описание которых содержит степени координат не выше двух, при решении обратных задач (в частности, при вычислении координат на поверхности тела, что необходимо, в том числе, для построения 2D-проекции) требуют всего лишь решения хорошо известного квадратного уравнения, содержащего операцию взятия квадратного корня. По этой причине вычислительная сложность в данном случае остается зачастую вполне приемлемой, и включение таких геометрических объектов в модель возможно. Ниже приводится пример эффективности такого подхода.

В общем случае в CAD/CAM-проектировании твердое тело принято описывать как комплексную полиповерхность, составленную из плоских (3D-полигонов) и криволинейных граней (частей сложных поверхностей, в том числе выше второго порядка, в узловых вершинах которых вычисляются нормали к поверхности). При этом конечная программная модель синтезируется как результат полного триангулирования исходной математической модели. Далее сформированный поток треугольников направляется на построение проекции, например с помощью стандартных средств OpenGL. Такой метод, будучи универсальным, приводит к заметной и неоправданной вычислительной нагрузке. Обсуждаются методы снижения количества полигонов в конечном представлении модели. Однако в рамках чисто триангуляционного подхода не удается достичь сколь-нибудь существенной оптимизации. Более детальное рассмотрение позволяет выделить квазивыпуклые области на криволинейных гранях, которые можно более эффективно аппроксимировать полигонами порядка выше трех, а чисто плоские грани (с общей единственной нормалью) — обрабатывать непосредственно на основе прямых растровых алгоритмов.

Другой, принципиально новый метод связан с вычислением 3D-координат вершин на моделируемой поверхности. При необходимости расширения класса криволинейных граней на произвольно формируемые поверхности обычно прибегают к стандартному подходу на основе сплайнового приближения (как правило, это бикубические 3D-сплайны). Найден более универсальный и эффективный подход на основе аппарата Фурье-аппроксимаций. Хорошо известно, что гладкие функциональные зависимости имеют эффективное разложение по базису Фурье (на основе гармонических функций). Так, обычный одномерный комплексный ряд Фурье имеет смысл аппроксимации замкнутого параметрического контура на обычной 2D-плоскости. При этом, чем выше степень гладкости такого контура, тем меньшим числом гармоник (компонент спектрального Фурье-разложения) он может быть представлен (то есть — может быть восстановлен обратным преобразованием с минимальными погрешностями). Тем самым достигается эффективное сжатие описания конечной координатной функции.

Применительно к построению комплексных, но достаточно гладких криволинейных поверхностей построено обобщение рядов Фурье для 3D-случая. При этом в качестве базиса используются операторы (матрицы 3Ѕ3) вращения вектора. Простейший пример связан с хорошо известной сферической системой координат. В этом случае фазовые углы поворота вектора являются одновременно координатами на вспомогательной плоскости развертки. Для представления произвольной сферы достаточно только двух спектральных базисных векторов и трех для другого простого примера — тора.

2.2 Обобщение методов векторного анализа

Из практики 3D-моделирования хорошо известно, что основным математическим инструментом в данной прикладной сфере является раздел математики, известный как векторный анализ. Это напрямую связано с вычислением координат проекций (на основе скалярного произведения векторов) либо, например, с определением векторов нормалей к поверхности (векторное произведение). В оптимизационных расчетах большую роль играет решение систем линейных уравнений, в частности для регрессионной аппроксимации. Последняя проблема обычно относится к более общему разделу линейной алгебры, где применяется понятие матриц. Однако оказалось возможным обобщить все указанные задачи на основе более полного раскрытия свойств векторных пространств, не прибегая к понятию матрицы.

Так, понятие векторного произведения в более общем виде имеет смысл построения ортогонального дополнения в некотором N-мерном векторном пространстве к базису в его (N – 1)-мерном подпространстве, которое может быть определено с точностью до ненулевого скалярного коэффициента. Стандартное в математике определение векторного произведения по сути представляет собой алгоритм наиболее простого нахождения подходящего ортогонального вектора для 3D-случая. Проблема выбора коэффициента при этом неявно снимается за счет удобного набора чисто линейных операций над координатами (умножения-сложения), то есть без нормирования.

Аналогичным образом проблема решения системы из N линейных уравнений сводится к обратной задаче восстановления вектора по его проекциям на некотором неортогональном ненормированном базисе (каждое уравнение представляет собой N-мерное скалярное произведение искомого неизвестного вектора с базисными, то есть попросту проекции). Решение в общем виде может быть представлено линейной комбинацией из N ортогональных дополнений (также с точностью до ненулевого скалярного коэффициента) ко всем N поднаборам из (N – 1)-мерных подпространств с коэффициентами, пропорциональными исходным проекциям (значениям в правой части системы). Наиболее простой алгоритм решения — ортогонализация (например, на основе хорошо известной процедуры Грама-Шмидта), нормирование и умножение результата на вектор проекций (правая часть системы). В сравнении с известным стандартным методом Гаусса-Жордана это дает более простой и быстрый результат. Относительный недостаток — необходимость взятия N квадратных корней при нормировании.

2.3 Инструментарий для программных реализаций

Программные пакеты, позволяющие создавать трёхмерную графику, то есть моделировать объекты виртуальной реальности и создавать на основе этих моделей изображения, очень разнообразны. Последние годы устойчивыми лидерами в этой области являются коммерческие продукты: такие как 3ds Max, Maya, Lightwave 3D, SoftImage XSI, Sidefx Houdini, Maxon Cinema 4D и сравнительно новые Rhinoceros 3D, modo, Nevercenter Silo или ZBrush. Кроме того, существуют и открытые продукты, распространяемые свободно, например, пакет Blender (позволяет делать и производство моделей, и последующий рендеринг), K-3D и Wings3D (только создание моделей с возможностью последующего использования их другими программами). Некоторое время назад Caligari закрыла разработки по trueSpace и она также стала бесплатной.

Бесплатная программа SketchUp позволяет создавать модели, совместимые с географическими ландшафтами ресурса Google Планета Земля, а также просматривать в интерактивном режиме на компьютере пользователя несколько тысяч архитектурных моделей, которые выложены на бесплатном постоянно пополняемом ресурсе Google Cities in Development (выдающиеся здания мира), созданные сообществом пользователей.

Трехмерная графика активно применяется в системах автоматизации проектных работ (САПР) для создания твердотельных элементов: зданий, деталей машин, механизмов, а также в архитектурной визуализации (сюда относится и так называемая "виртуальная археология"). Широко применяется 3D графика и в современных системах медицинской визуализации.

2.4 Применение 3 d на уроках геометрии

С появлением 3dтехнологий у нас появилась возможность наглядно демонстрировать геометрические тела по средствам ИКТ. Изучение 4-мерных геометрических тел затруднительно в силу отсутствия возможности работать с их материальными моделями. Но становится возможным представить их по проекциям на гиперплоскость, демонстрируемым компьютерной программой. С помощью этой программы очень красиво может быть решена задача 4-мерного куба и других объемных геометрических тел. Трехмерные модели можно создавать не только для реализации их в специализированном программном обеспечении, но и создать анимированный видеоролик. Это позволит демонстрировать тела вращения, просмотр фигуры с различных ракурсов, как происходит сечение фигур и многие другие их свойства.

Преимущество видеоролика в том, что его можно демонстрировать и без компьютера. Достаточно иметь лишь телевизор и видеопроигрыватель. Так же этот ролик можно записать и на аналоговый носитель, если нет возможности воспроизвести его на цифровом проигрывателе, но есть видеомагнитофон. Именно поэтому я и решил создать именно видео файлы потому, что они просты и удобны в реализации.

Глава 3. Геометрические тела и их отображение

Геометрическое тело рассматривают как множество всех принадлежащих ему точек, связанных между собой и ограниченных в пространстве соответствующим образом. Оно может перемещаться в пространстве без изменения взаимного положения его элементов.

В инженерной графике рассматриваются одномерные тела (отрезок линии), двухмерные (плоская фигура, отсек поверхности), трехмерные (любая объемная фигура). Основными предметами изображения на плоских чертежах являются трехмерные геометрические тела, окружающие нас в реальном трехмерном пространстве.

Сложные геометрические тела можно рассматривать и как состоящие из более простых трехмерных фигур, которые определяются основными формообразующими элементами пространства — точками, линиями, поверхностями.

Геометрические тела на чертежах получают методом отображения (Рис. 1). Отображение геометрического тела — это понятие, в соответствии с которым каждой точке трехмерного пространства соответствует конкретная точка двухмерного пространства на чертеже. Отображение геометрических тел может быть выполнено на плоскость или какую-либо другую поверхность. В курсе инженерной графики рассматривается отображение геометрических тел на плоскость. Изображение геометрического тела на плоскости можно получить путем проецирования ее точек на эту плоскость.

Геометрическая связь между геометрическим телом, расположенным в пространстве, и его отображением на чертеже на плоскости устанавливаются по законам проецирования, которые базируются на принципе взаимно-однозначного соответствия.

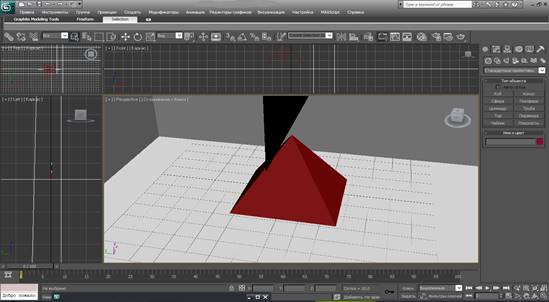
Рис. 1 3D отображение геометрического тела.

3.1 Параллельные прямые

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися (Рис. 2).

Теорема: через точку вне данной прямой можно провести прямую, параллельную данной и только одну

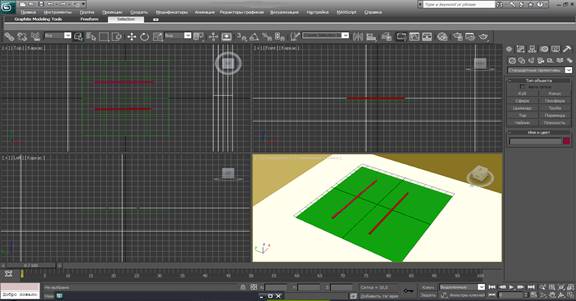
Рис. 2 3D отображение параллельных прямых.

3.2 Параллелепипед, его элементы

Если основание призмы - параллелограмм, то она называется параллелепипедом (Рис. 3). У параллелепипеда все грани - параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.

Параллелепипед бывает прямой и наклонный.

Прямой параллелепипед: основание - прямоугольник. У него все грани - прямоугольники. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом. Длины непараллельных ребер прямоугольный параллелепипед называются его линейными размерами (измерениями). У прямоугольный параллелепипед три измерения.

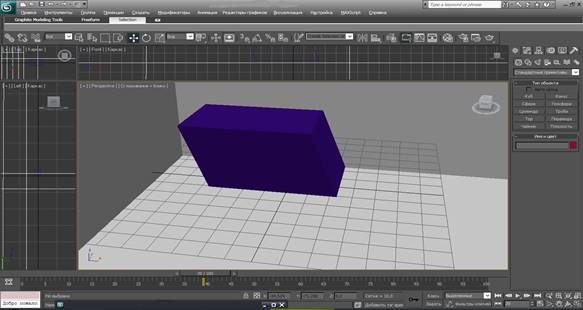
Рис. 3 3D отображение параллелепипеда.

3.3 Параллельные плоскости

Две плоскости называются параллельными, если они не пересекаются (Рис. 4).

Теорема: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

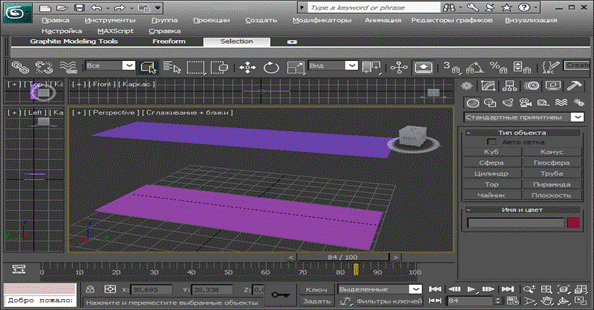
Рис.4 3D отображение параллельных плоскостей.

3.4 Перпендикулярные плоскости.

Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым (Рис. 5).

Теорема: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Рис. 5 3D отображение перпендикулярных плоскостей.

Заключение

ИКТ создает большие возможности в формировании персонального когнитивного стиля. В частности, посредством различных мультимедийных средств (2D и 3D графика, звук, гипертекстовая форма) становится возможной разработка учебных текстов с учетом различных стилей кодирования информации: предметно-практического, визуального, словесно-речевого, сенсорно-эмоционального, что, в конечном счете, способствует индивидуализации процесса обучения.

Говоря о практическом использования ИКТ в школе и вузе, обращает на себя внимание тот факт, что на сегодняшний день этот вопрос недостаточно исследован. Опрос, проведенный среди преподавателей математических дисциплин вузов Орла, Курска, Брянска, Железногорска, Тулы показал, что лишь 41,9% из них используют компьютерные средства в преподавании, а среди учителей Екатеринбурга и Омска эта доля составляет 23,7%. Как видим, исследование проводилось только по одному из двух направлений (т.е. либо в школе, либо в вузе). Хотелось бы отметить и тот факт, что в большинстве публикаций по вопросу использования ИКТ акцент ставится на отсутствие методического обеспечения существующих компьютерных средств. По-нашему мнению, следует обратить внимание как на количество, так и на качество уже имеющихся. Например, часто электронный учебник является просто копией «бумажного» варианта и содержит грубые ошибки в изображениях геометрических фигур.

Применение 3d технологий позволяет наглядно показать такие сложные элементы как преобразование одной фигуры в другую, и сечение одной или несколькими плоскостями что может быть наглядным примером для учащихся школ и вузов.

Модели фигур в трехмерном пространстве можно предоставлять как в программном виде(в какой либо программе) так и посредствам видеороликов. Преимущество видео в том, что его можно демонстрировать не только на компьютере но и по средствам простого видеопроигрывателе, а так же записать на аналоговые носители. Именно по этому я решил разработать свой проект так , чтобы его можно было представить в видео файлах.

В курсовой работе я постарался реализовать поставленные задачи, для этого:

· Было изучено содержание рассматриваемой темы, описанной в источниках различных авторов

· Обоснованно выбран программный продукт, с помощью которого и были созданы видеоролики.

Литература

1. Адамар, Ж. Элементарная геометрия. Часть вторая. Стереометрия. [Текст] / Ж. Адамар. - М.: Учпедгиз, 1948

2. Ильин, В. А. Аналитическая геометрия. [Текст] / В. А. Ильин, Э. Г. Позняк. - М.: Наука. Физматлит, 2003

3. Романычева, Э. Т. Инженерная и компьютерная графика [Текст] / Э. Т. Романычева, Т. Ю. Соколова, Г. Ф. Шандурина. – М.: ДМК Пресс, 2001

4. Большой энциклопедический словарь. Математика. [Текст] / - М.: Большая Российская энциклопедия, 1998

5. Ким Ли 3DStudioMAXдля дизайнера. Искусство трехмерной анимации [Текст] / Ким Ли. – М.: ДиаСофт, 2003

6. Ильиных, Д. В. Дидактическая компьютерная игра в процессе изучения правильных многогранников [Текст] / Д. В. Ильиных, Р. Ф. Мамалыга – Челябинск, ЧГПУ, 2006

7. Мамалыга, Р. Ф. Один из аспектов развития пространственного мышления [Текст] / Р. Ф. Мамалыга – Пермь, ПГПУ, 2004.

8. Материалы XIV Международной конференции «Математика. Компьютер. Образование». – Пущино, 2007

9. Компьютерная графика [Электронный ресурс]: Режим доступа: http://www.codenet.ru свободный

10. Самоучитель AUTODESK 3DS MAX 9 [Электронный ресурс]: Режим доступа: http://samouchka.net свободный