Реферат: Генетические алгоритмы 2

АННОТАЦИЯ

Генетические алгоритмы в настоящее время широко используются для интеллектуальной обработки данных и решения задач оптимизации и поиска. Они успешно используются для решения ряда экономически значимых задач в бизнесе и инженерных разработках. Финансовые компании широко используют генетические алгоритмы для прогнозирования развития финансовых рынков.

Задачи оптимизации – один из самых важных классов задач практического характера, с которыми мы сталкиваемся ежедневно на работе, или в быту.

Что такое генетические алгоритмы, и каким образом генетические алгоритмы можно использовать для решения задач оптимизации, предлагается выяснить в ходе данной курсовой работы.

The Genetic algorithms are broadly used for intellectual data processing and decisions of the problems optimization and of searching for at present times. They are successfully used for decision of the economic significant problems in business and engineering development. The Financial companies broadly use the genetic algorithms for forecasting of the development the financial.

The problems of optimization are one of the most important classes of the problems of the practical character. We have deal with these problems every day at work and at home.

What are the genetic algorithms and how can we use the genetic algorithms for decision of the problems of optimization is offered realize in this scientific work.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 4

ГЛАВА 1 ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ.. 7

1.1 Генетический алгоритм и его особенности. 7

1.2 Основные генетические операторы.. 10

1.3 Работа генетического алгоритма. 12

1.4 Вывод к Главе 1. 16

ГЛАВА 2 ЗАДАЧИ ОПТИМИЗАЦИИ.. 17

2.1 Задачи, решаемые с помощью генетических алгоритмов. 17

2.2 Математическая постановка задачи оптимизации. 18

2.3 Пути решения оптимизационных задач. 19

2.4 Вывод к Главе 2. 21

ГЛАВА З РАЗРАБОТКА УЧЕБНОГО ЭЛЕКТРОННОГО ПОСОБИЯ ПО ГЕНЕТИЧЕСКИМ АЛГОРИТМАМ.. 23

3.1 Обоснование выбора программного обеспечения. 23

3.1 Описание программной реализации. 24

ЗАКЛЮЧЕНИЕ. 27

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 29

ПРИЛОЖЕНИЕ А.. 30

ВВЕДЕНИЕ

Мир, который нас окружает, является очень сложной системой, которую пытается разгадать человек. Наука объясняет окружающее и помогает приспособиться к новой информации, получаемой из внешней среды. Многое из того, что мы видим и наблюдаем, можно объяснить теорией эволюции через наследственность, изменение и отбор.

На мировоззрение людей сильно повлияла теория эволюции Чарльза Дарвина, представленная в работе "Происхождение Видов", в 1859 году. Множество областей научного знания многим обязано революции, вызванной теорией эволюции и развития. Дарвин обнаружил главный механизм развития: отбор в соединении с изменчивостью, который объясняет очень широкий спектр явлений, которые мы наблюдаем в природе. Поэтому ученые, которые занимались компьютерными исследованиями, также обращались к теории эволюции. Возможность того, что вычислительная система, наделенная простыми механизмами изменчивости и отбора, могла бы функционировать по аналогии с законами эволюции в естественных системах, была очень заманчивой. Она является причиной появления ряда вычислительных систем, построенных на принципах естественного отбора.

В природе постоянно происходит процесс решения задач оптимизации, которые являются одним из самых важных практических классов. Их приходится решать каждому из нас на работе и в быту.

Благодаря открытиям, которые делают ученые, современной науке известны все основные механизмы эволюции, связанные с генетическим наследованием. Эти механизмы достаточно просты по своей идее, но довольно эффективны. Простое моделирование эволюционного процесса на компьютере позволяет получить решения многих практических задач. Такие модели получили название “генетические алгоритмы” и уже широко применяются в различных областях.

В настоящее время в мире происходят постоянные изменения стратегий и методов решения задач разной направленности. Среди этих задач есть задачи, решаемые простым путем, но есть и такие, точное решение которых найти практически невозможно. Именно в таких случаях применяются генетические алгоритмы. Они являются эффективной процедурой поиска, которая конкурирует с другими процедурами. Поэтому проблематика исследования по теме «Генетические алгоритмы» несет актуальный характер

Объектом исследования данной курсовой работы являются генетические алгоритмы.

Предметом исследования является применение генетических алгоритмов для нахождения решения задач оптимизации.

Цель курсовой работы – разработкаучебного электронного пособия, в котором последовательно описываются основные аспекты генетических алгоритмов, а также то, каким образом их можно применять при решении задач оптимизации.

В ходе исследования поставлены следующие задачи :

1. Сформировать общие представления о генетических алгоритмах

и их особенностях;

2. Выяснить, какие существуют генетические операторы;

3. Узнать, каким образом происходит работа генетического алгоритма

и его реализация;

4. Узнать, где могут применяться генетические алгоритмы;

5. Выяснить какие задачи могут решаться с помощью генетических

алгоритмов;

6. Выявить пути решения задач оптимизации с помощью генетических

алгоритмов;

7. На основе полученной информации создать электронное пособие по

основам генетических алгоритмов.

Перед началом работы была выдвинута гипотеза – решение задач оптимизации возможно с помощью генетических алгоритмов. Эта гипотеза будет подтверждена или опровергнута в ходе исследования.

Курсовая работа состоит из введения, трех глав основной части, заключения, приложения и библиографического списка.

Во введении обоснована актуальность выбора темы, определены предмет, объект, цель и соответствующие ей задачи исследования, выявлена проблема и поставлена гипотеза.

В первой главе рассмотрены общетеоретические вопросы по теме «Генетические алгоритмы». В ней рассматривается, что такое геометрические алгоритмы, каковы их особенности, какие существуют генетические операторы, как работают геометрические алгоритмы.

Во второй главе рассмотрены вопросы, касающиеся задач оптимизации и применения генетических алгоритмов для решения задач такого класса. В ней рассматриваются задачи, которые можно решать с помощью генетических алгоритмов, математическая постановка задач оптимизации и пути их решения.

Третья глава имеет практический характер. В ней описана программная реализация создания электронного пособия по теме «Генетические алгоритмы». В приложении описан программный код реализации одной их классических оптимизационных задач, решенной с помощью генетического алгоритма – «Задачи коммивояжера». После каждой главы идут обобщающие выводы.

ГЛАВА 1 ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ

1.1 Генетический алгоритм и его особенности

Генетические алгоритмы возникли в результате наблюдения и попыток копирования естественных процессов, происходящих в мире живых организмов, в частности, эволюции и связанной с ней селекции (естественного отбора) популяций живых существ.

Идею генетических алгоритмов высказал Джон Холланд в 1975 году. Он заинтересовался свойствами процессов естественной эволюции, в том числе фактом, что эволюционируют хромосомы, а не сами живые существа. Холланд был уверен в возможности составить и реализовать в виде компьютерной программы алгоритм, который будет решать сложные задачи так, как это делает природа - путем эволюции. Поэтому он начал трудиться над алгоритмами, оперировавшими последовательностями двоичных цифр (единиц и нулей), получившими название хромосом. Эти алгоритмы имитировали эволюционные процессы в поколениях таких хромосом. Так же, как и в природе, генетические алгоритмы осуществляли поиск "хороших" хромосом без использования какой-либо информации о характере решаемой задачи. Требовалась только некая оценка каждой хромосомы, отражающая ее приспособленность. [7]

Генетические алгоритмы применяются при разработке программного обеспечения, в системах искусственного интеллекта, оптимизации, искусственных нейронных сетях и в других отраслях знаний. Следует отметить, что с их помощью решаются задачи, для которых ранее использовались только нейронные сети. В этом случае генетические алгоритмы выступают просто в роли независимого от нейронных сетей альтернативного метода, предназначенного для решения той же самой задачи. Генетические алгоритмы часто используются совместно с нейронными сетями. Они могут поддерживать

нейронные сети или наоборот, либо оба метода взаимодействуют в рамках гибридной системы, предназначенной для решения конкретной задачи. Генетические алгоритмы также применяются совместно с нечеткими системами.

Генетические алгоритмы - адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течение нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный", открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы.

Основной закон наследования интуитивно понятен каждому - он состоит в том, что потомки похожи на родителей. В частности, потомки более приспособленных родителей будут, скорее всего, одними из наиболее приспособленных особей в своем поколении. Из биологии мы знаем, что любой организм может быть представлен своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе. Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. Все дальнейшее функционирование механизмов генетического алгоритма производится на уровне генотипа, позволяя обойтись без информации о внутренней структуре объекта, что и обуславливает его широкое применение в самых разных задачах. [6]

В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются битовые строки. При этом каждому атрибуту объекта в фенотипе соответствует один ген в генотипе объекта. Ген представляет собой битовую строку, чаще всего фиксированной длины, которая представляет собой значение этого признака.

Для кодирования таких признаков можно использовать самый простой вариант – битовое значение этого признака. Тогда будет весьма просто использовать ген определенной длины, достаточной для представления всех возможных значений такого признака.

Таким образом, для того, чтобы определить фенотип объекта (то есть значения признаков, описывающих объект) нам необходимо только знать значения генов, соответствующим этим признакам, то есть генотип объекта. При этом совокупность генов, описывающих генотип объекта, представляет собой хромосому. В некоторых реализациях ее также называют особью. В реализации генетического алгоритма хромосома представляет собой битовую строку фиксированной длины. При этом каждому участку строки соответствует ген. Длина генов внутри хромосомы может быть одинаковой или различной. Чаще всего применяют гены одинаковой длины. [9]

Генетические алгоритмы работают с совокупностью "особей" – популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы. Наиболее приспособленные особи получают возможность "воспроизводить" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции. Иногда происходят мутации, или спонтанные изменения в генах.[13]

Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге популяция будет сходиться к оптимальному решению задачи. Преимущество генетических алгоритмов состоит в том, что он находит приблизительные оптимальные решения за относительно короткое время.

Генетический алгоритм состоит из следующих компонент:

· Хромосома. Решение рассматриваемой проблемы. Состоит из генов.

· Начальная популяция хромосом.

· Набор операторов для генерации новых решений из предыдущей

популяции.

· Целевая функция для оценки приспособленности решений. [11]

1.2 Основные генетические операторы

Стандартные операторы для всех типов генетических алгоритмов это:скрещивание, мутация и селекция.

Как известно в теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). Этот оператор определяет передачу признаков родителей потомкам.

Действует он следующим образом:

1. Из популяции выбираются две особи, которые будут родителями;

2. Определяется (обычно случайным образом) точка разрыва;

3. Потомок определяется как конкатенация части первого и второго родителя.

Таким образом, оператор скрещивание осуществляет обмен частями хромосом между двумя хромосомами в популяции, т. е. создает структуру, основанную на двух структурах – заменой одной части первой структуры на туже область во второй. Затем с вероятностью 0.5 определяется одна из результирующих хромосом в качестве потомка.

Следующий генетический оператор предназначен для того, чтобы поддерживать разнообразие особей в популяции. Он называется мутацией .

При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется.Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами.

Можно сказать, что инверсия - перестановка в структуре некоторой ее части наоборот, а мутация - стохастическое изменение части хромосом, когда каждый ген строки, которая подвергается мутации, с вероятностью P_mut (обычно очень маленькой) меняется на другой ген.

Для функционирования генетического алгоритма достаточно этих двух генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации этих двух операторов. Например, кроссовер может быть не одноточечный (с одной точкой разрыва), а многоточечный, когда формируется несколько точек разрыва (чаще всего две). Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.

Оператор селекции осуществляет отбор хромосом в соответствии со значениями их функции приспособленности.

Наиболее эффективные два механизма отбора – элитный отбор и отбор с вытеснением.

Идея элитного отбора основана на построении новой популяции только из лучших особей репродукционной группы, объединяющей в себе родителей, их потомков и мутантов. В основном это объясняют потенциальной опасностью преждевременной сходимости, отдавая предпочтение пропорциональному отбору. Быстрая сходимость, обеспечиваемая элитным отбором, может быть, когда это необходимо, с успехом компенсирована подходящим методом выбора родительских пар, например аутбридингом. Именно такая комбинация "аутбридинг - элитный отбор" является одной из наиболее эффективных. [3]

Второй метод – это отбор вытеснением. Будет ли особь из репродукционной группы заноситься в популяцию нового поколения, определяется не только величиной ее приспособленности, но и тем, есть ли уже в формируемой популяции следующего поколения особь с аналогичным хромосомным набором. Из всех особей с одинаковыми генотипами предпочтение сначала, конечно же, отдается тем, чья приспособленность выше.

Таким образом, достигаются две цели: во-первых, не теряются лучшие найденные решения, обладающие различными хромосомными наборами, а во-вторых, в популяции постоянно поддерживается достаточное генетическое разнообразие. [8]

1.3 Работа генетического алгоритма

Работа генетического алгоритма представляет собой итерационный процесс, который продолжается до тех пор, пока не выполнятся заданное число поколений или какой-либо иной критерий останова. На каждом поколении генетическим алгоритмом реализуется отбор пропорционально приспособленности, кроссовер и мутация.

Схематичное описание функционирования генетического алгоритма (Рисунок 1):

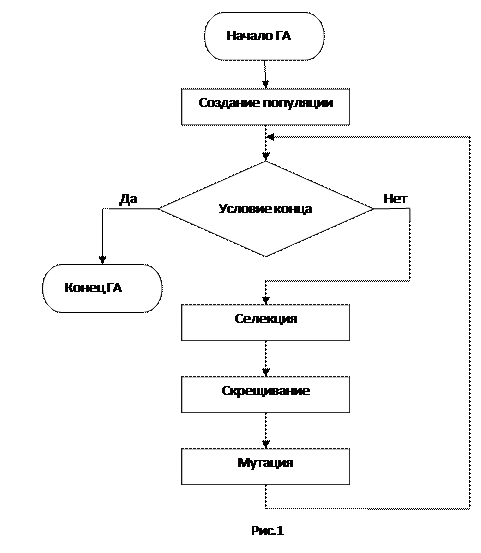
Рисунок 1 Алгоритм работы классического генетического алгоритма

Функционирование генетического алгоритма можно описать следующими шагами:

Инициировать начальный момент времени t=0. Случайным образом сформировать начальную популяцию, состоящую из k-особей.

Вычислить приспособленность каждой особи и популяции в целом. Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.

1. Выбрать особь из популяции;

2. С определенной вероятностью (вероятностью кроссовера) выбрать вторую особь из популяции и произвести оператор кроссовера;

3. С определенной вероятностью (вероятностью мутации) выполнить оператор мутации;

4. С определенной вероятностью (вероятностью инверсии) выполнить оператор инверсии;

5. Поместить полученную хромосому в новую популяцию;

6. Выполнить операции, начиная с пункта 3, k-раз;

7. Увеличить номер текущей эпохи t=t+1;

8. Если выполнилось условие остановки, то завершить работу, иначе переход на шаг 2;

Распишем более подробно следующие этапы:

1. Выбор родительской пары:

Первый подход самый простой – это случайный выбор родительской пары, когда обе особи, которые составят родительскую пару, случайным образом выбираются из всей популяции, причем любая особь может стать членом нескольких пар. Несмотря на простоту, такой подход универсален для решения различных классов задач. Однако он достаточно критичен к численности популяции, поскольку эффективность алгоритма, реализующего такой подход, снижается с ростом численности популяции.

Второй способ выбора особей в родительскую пару - так называемый селективный. Его суть состоит в том, что "родителями" могут стать только те особи, значение приспособленности которых не меньше среднего значения приспособленности по популяции, при равной вероятности таких кандидатов составить брачную пару. Такой подход обеспечивает более быструю сходимость алгоритма. Однако из-за быстрой сходимости селективный выбор родительской пары не подходит тогда, когда ставиться задача определения

нескольких экстремумов, поскольку для таких задач алгоритм, как правило, быстро сходится к одному из решений.

Другие два способа формирования родительской пары – инбридинг и аутбридинг. Оба эти метода построены на формировании пары на основе близкого и дальнего "родства" соответственно. Под "родством" здесь понимается расстояние между членами популяции как в смысле геометрического расстояния особей в пространстве параметров. В связи с этим различают генотипный и фенотипный (или географический) инбридинг и аутбридинг. Под инбридингом понимается такой метод, когда первый член пары выбирается случайно, а вторым с большей вероятностью будет максимально близкая к нему особь. Аутбридинг же, наоборот, формирует брачные пары из максимально далеких особей. Использование генетических инбридинга и аутбридинга оказалось более эффективным по сравнению с географическим для всех тестовых функций при различных параметрах алгоритма. Наиболее полезно применение обоих представленных методов для многоэкстремальных задач. Однако два этих способа по-разному влияют на поведение генетического алгоритма. Так инбридинг можно охарактеризовать свойством концентрации поиска в локальных узлах, что фактически приводит к разбиению популяции на отдельные локальные группы вокруг подозрительных на экстремум участков ландшафта, напротив аутбридинг как раз направлен на предупреждение сходимости алгоритма к уже найденным решениям, заставляя алгоритм просматривать новые, неисследованные области. [10]

2. Механизм отбора:

Обсуждение вопроса о влиянии метода создания родительских пар на поведение генетического алгоритма, невозможно вести в отрыве от реализуемого механизма отбора при формировании нового поколения. Наиболее эффективные два механизма отбора элитный и отбор с вытеснением, которые были рассмотрены в предыдущем пункте.

В последние годы, реализовано много генетических алгоритмов и в большинстве случаев они мало похожи на алгоритм, представленный на рис.5. По этой причине в настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов.[2]

1.4 Вывод к Главе 1

При рассмотрении общих теоретических аспектов по теме «Генетические алгоритмы», выяснилось, что идея создания алгоритмов, которые могли бы решать разного рода задачи, в том числе и оптимизационные, принадлежит Джону Холланду. В 1975 году им был предложен первый генетический алгоритм. Холланд занимался разработкой алгоритмов, которые могли бы использовать механизмы естественного отбора при решении задач.

В общих чертах работу генетического алгоритма можно описать так: он создает популяцию особей, каждая из которых является решением задачи, а затем эти особи эволюционируют по принципу «выживает сильнейший», то есть остаются лишь самые оптимальные решения. Каждую особь описывает хромосома, хромосома состоит из генов, которые располагаются в определенных позициях хромосомы, т.е. вся наследственная информация, или генотип, хранится в хромосомах.

Работа генетического алгоритма имитирует естественную жизнь, только сильно упрощенную.

Генетические алгоритмы создавались как еще один метод решения задач, альтернативный уже существующим. Чаще всего генетические алгоритмы используют для решения оптимизационных задач, особенно, если традиционными способами эти задачи решить очень трудно, практически невозможно. В следующей главе будут рассмотрены оптимизационные задачи и то, каким образом их можно решить с помощью генетического алгоритма.

ГЛАВА 2 ЗАДАЧИ ОПТИМИЗАЦИИ

2.1 Задачи, решаемые с помощью генетических алгоритмов

Итак, в этой главе нами будут рассмотрены задачи оптимизации, их математическая постановка и пути решения.

Задачи оптимизации – наиболее распространенный и важный для практики класс задач. Их приходится решать любому из нас или в быту, распределяя свое время между разными делами, или на работе, добиваясь максимальной скорости работы программы или максимальной прибыльности компании.

Среди этих задач есть те, которые решаются простым путем, но есть и такие, точное решение которых найти практически невозможно.

Генетические алгоритмы в разных формах применяются к решению многих научных и технических проблем. Генетические алгоритмы используются при создании других вычислительных структур, например, автоматов или сетей сортировки. В машинном обучении они используются при проектировании нейронных сетей или управлении роботами. Они также применяются при моделировании развития в разных предметных областях, включая биологические (экология, иммунология и популярная генетика) и социальные (такие как экономика и политические системы) системы.

Тем не менее, популярное применение генетических алгоритмов – оптимизация многопараметрических функций. Большинство реальных задач могут быть сформулированы, как поиск оптимального значения, где значение – сложная функция, зависящая от определенных входных параметров. В некоторых случаях, нужно найти те значения параметров, при которых достигается точное значение функции. В других случаях, точный оптимум не нужен – решением может считаться любое значение, лучшее за определенную заданную величину. В этом случае, генетические алгоритмы – приемлемый метод для поиска "приемлемых" значений. Сила генетического алгоритма состоит в его способности манипулировать одновременно многими параметрами, которая используется в сотнях прикладных программ, включая проектирование самолетов, настраивании параметров алгоритмов и поиске стойких состояний систем нелинейных дифференциальных уравнений.

Генетические алгоритмы являются эффективной процедурой поиска, которая конкурирует с другими процедурами. Эффективность генетических алгоритмов сильно зависит от таких деталей, как метод кодирования решений, операторов, настраивания параметров, отдельных критериев успеха. [1]

2.2 Математическая постановка задачи оптимизации

Постановка задачи оптимизации включает в себя множество допустимых решений и числовую функцию, определенную на этом множестве, которая называется целевой функцией.

Нельзя отождествлять критерий (критерии) оптимальности и целевую функцию.

Целевая функция – это аналитическая зависимость между критерием (критериями) оптимальности и подлежащими оптимизации параметрами с указанием направления экстремума.

Отличие понятий «критерий» и «целевая функция» состоит в следующем:

1. Целевая функция может включать в себя более одного критерия.

2. Для целевой функции всегда и обязательно указывается вид

экстремума:

Различают два вида задач оптимизации:

1. Задачу минимизации.

2. Задачу максимизации.

Чтобы решить задачу минимизации функции на множестве, необходимо найти такой вектор (а также соответствующее значение целевой функции), чтобы неравенство: выполнялось для всех. При этом называют оптимальным решением (точнее здесь – минимальным решением), а - оптимумом (минимумом).

Чтобы решить задачу максимизации функции на множестве, необходимо найти такой вектор (а также соответствующее значение целевой функции), чтобы неравенство: выполнялось для всех. При этом называют оптимальным (максимальным ) решением, а– оптимумом ( максимумом ).

В общем виде находится именно вектор, т.к., например, при решении двухпараметрической задачи, он будет включать в себя два параметра, трехпараметрической – три параметра и т.д. [1]

2.3 Пути решения оптимизационных задач

Генетический алгоритм - новейший, но не единственно возможный способ решения задач оптимизации. С давних пор известны два основных пути решения таких задач - переборный и локально-градиентный. У этих методов свои достоинства и недостатки, и в каждом конкретном случае следует подумать, какой из них выбрать.

Переборный метод наиболее прост по своей сути. Для поиска оптимального решения (точки максимума целевой функции) требуется последовательно вычислить значения целевой функции во всех возможных точках, запоминая максимальное из них.

Недостатком этого метода является большая вычислительная стоимость. В частности, в задаче коммивояжера потребуется просчитать длины более 1030 вариантов путей, что совершенно нереально. Однако, если перебор всех вариантов за разумное время возможен, то можно быть абсолютно уверенным в том, что найденное решение действительно оптимально.

Второй популярный способ основан на методе градиентного спуска. При этом вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. Достигнув локального максимума, такой алгоритм останавливается, поэтому для поиска глобального оптимума потребуются дополнительные усилия.

Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же - глобальный).

Типичная практическая задача, как правило, мультимодальна и многомерна, то есть содержит много параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение. [1]

Генетический алгоритм представляет собой комбинацию переборного и градиентного методов. Механизмы кроссинговера (скрещивания) и мутации реализуют переборную часть, а отбор лучших решений – градиентный спуск.

То есть, если на некотором множестве задана сложная функция от нескольких переменных, тогда генетический алгоритм является программой, которая за допустимое время находит точку, где значение функции находится довольно близко к максимально возможному значению. Выбирая приемлемое время расчета, получаем лучшие решения, которые можно получить за это время. [5]

2.4 Вывод к Главе 2

Существует множество вариантов задач оптимизации. Особенно трудно переоценить их значимость в математической экономике. Во второй главе были рассмотрены задачи, которые можно решать с помощью генетических алгоритмов.

Существует вопрос о том, насколько целесообразно применение генетических алгоритмов для решения различных задач. С одной стороны, в математике существует достаточно большой класс абсолютно надежных (в смысле гарантии получения точного решения) методов решения различных задач. С другой стороны, речь идет о действительно сложных практических задачах, в которых эти надежные методы часто неприменимы. Нередко эти задачи выглядят настолько необозримыми, что не предпринимается даже попыток их осмысленного решения.

Например, фирма, занимающаяся транспортными перевозками, в современных условиях российского бизнеса скорее предпочтет нанять лишних водителей и повысить цены на свои услуги, чем оптимизировать маршруты и расписания поездок. На западном рынке, где уже давно действуют законы более или менее честной конкуренции, оптимальность деятельности компании значительно влияет на ее доходы и даже может стать решающим фактором для ее выживания. Поэтому любые идеи, позволяющие компании стать “умнее” своих конкурентов, находят там широкое применение.

Генетические алгоритмы — реализация одной из наиболее популярных идей такого рода. Таким образом, задав условия жизни в некотором виртуальном мире и заселив его представителями с определенными свойствами, после процессов скрещивания, мутации и естественного отбора, аналоги которых происходят и в реальном мире, мы стабильно получаем особь, свойства которой отвечают ранее заданным требованиям. Этот факт говорит о том, что понимание проверенных веками законов природы позволяет использовать их при решении, казалось бы, и далеких от нее задач, частным случаем которых являются задачи оптимизации.

Задачи оптимизации – наиболее распространенный и важный для практики класс задач. Их приходится решать любому из нас или в быту, распределяя свое время между разными делами, или на работе. Была рассмотрена математическая постановка задач оптимизации, а также пути их решения. Для решения задач оптимизации используются не только такие методы, как простой перебор и градиентный спуск, которые не всегда эффективны, особенно, если мы имеем дело с трудными в практическом смысле задачами.

Генетические алгоритмы достаточно эффективный способ решения непростых оптимизационных задач, поскольку сочетает в себе комбинацию переборного и градиентного методов. Механизмы кроссинговера (скрещивания) и мутации реализуют переборную часть, а отбор лучших решений – градиентный спуск.

Выбирая приемлемое время расчета, получаем лучшие решения, которые можно получить за это время.

ГЛАВА З РАЗРАБОТКА УЧЕБНОГО ЭЛЕКТРОННОГО ПОСОБИЯ ПО ГЕНЕТИЧЕСКИМ АЛГОРИТМАМ

3.1 Обоснование выбора программного обеспечения

В последнее время резко возрос интерес к программированию. Это свя­зано с развитием и внедрением в повседневную жизнь информационно-коммуникационных технологий. Если человек имеет дело с компьютером, то рано или поздно у него возникает желание, а иногда и необходимость, программировать.

Интерактивность – сегодня очень важное условие для создаваемых приложений, программ, электронных пособий и т. д. Наиболее полный стандарт, который гарантирует данное условие, ActionScript для Flash. Сравнительно недавно он превратился из простого языка подготовки сценариев в полноценную объектно-ориентированную среду программирования.

Нашей целью является создание электронного пособия, которое позволило бы достаточно понятно и просто донести до пользователя основные понятия и принципы организации генетического алгоритма и решения с его помощью оптимизационных задач, в частности, задачи коммивояжера, которая является классической оптимизационной задачей. ActionScript предоставляет прекрасную возможность организовать красочный, доступный интерфейс и навигацию. И еще один неоспоримый плюс при создании учебника на ActionScript: использование готового продукта, как самостоятельную программу (публикация готового продукта с .exe расширением).

Поэтому для создания электронного пособия по основам генетических алгоритмов был выбран Flash.

Для того, чтобы показать, как реализуется генетический алгоритм при решении задачи коммивояжера, была выбрана среда программирования BorlandDelphi 6.0.

3.1 Описание программной реализации

Перед началом разработки электронного пособия был подготовлен материал, который будет представлен в нем. Главным критерием при отборе материала стала его полезность и возможность рассказать о генетических алгоритмах и задачах оптимизации в общих чертах на доступном языке.

Затем были определены структура и дизайн пособия.

Электронное учебное пособие создавалась с помощью MacromediaFlashMX2004.

Размещение материала было сформировано наподобие обычной книги с заглавием, содержанием и возможностью перелистывания страниц.

На первой странице было размещено название пособия и его содержание. Содержание состоит из трех пунктов, которые в свою очередь делятся на подпункты, позволяющие осветить рассматриваемую тему с нескольких сторон (Рисунок 2):

Рисунок 2 Содержание электронного пособия

Перелистывание между слайдам осуществляется за счет навигации в виде двух стрелок «вперед»-«назад», расположенных в правом нижнем углу. Кроме того, всегда существует возможность вернуться к странице содержания с любой страницы пособия. Для этого достаточно воспользоваться кнопкой «Main». Для того, чтобы кнопки навигации работали, на них был написан сценарий на ActionScript.

Подпункты на странице содержания выполнены в виде ссылок. Достаточно нажать на интересующий вопрос и откроется его страничка.

Каждый пункт и подпункт презентации расположен на отдельной странице. Для презентации был выбран нейтральный голубой фон. Вся цветовая гамма выдержана. Шрифты были подобраны таким образом, чтобы можно было прочитать без затруднений. В презентации присутствуют рисунки и таблицы, более наглядно объясняющие те или иные аспекты вопроса (Рисунок 3):

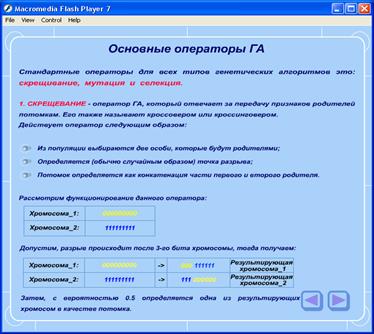
Рисунок 3 Пример страницы с наглядными пояснениями

И, наконец, на последнем шаге мы публикуем наше пособие в .exe формате, для того, чтоб наша разработка запускалась на компьютере любого пользователя, в не зависимости от того, установлен на его компьютере Flash или нет.

В электронном пособии в качестве примера оптимизационной задачи, которую можно решить с помощью генетического алгоритма, представлена задача коммивояжера. Для иллюстрации реализации генетического алгоритма при решении задачи была создана программа в BorlandDelphi 6.0, которая, в частности показывает решение задачи, представленной в электронном пособии (Рисунок 4):

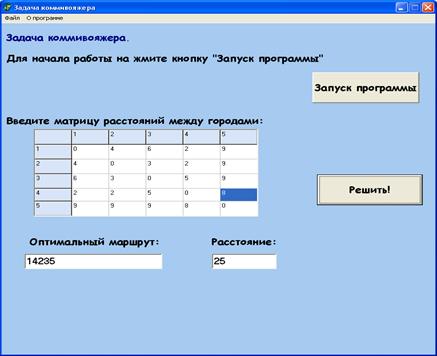
Рисунок 4 Реализация задачи коммивояжера с помощью генетического алгоритма

Программный код решения задачи коммивояжера описан в Приложении А.

ЗАКЛЮЧЕНИЕ

При исследовании вопроса о применении генетических алгоритмов для решения задач оптимизации, мы рассмотрели достаточное количество аспектов этой темы. Во-первых, выяснили общую теоретическую информацию, узнали кто, когда и зачем придумал генетические алгоритмы, что они из себя представляют, и какую имеют аналогию с естественным отбором в природе. Также мы узнали принцип работы генетических алгоритмов и то, при помощи каких основных операторов она осуществляется.

Также было выяснено, какие задачи можно решать с помощью генетических алгоритмов. Среди таких задач находятся и особый класс – оптимизационные.

Были рассмотрены пути решения оптимизационных задач. Кроме генетических алгоритмов используются также метод перебора и градиентный спуск. Генетические алгоритмы хороши тем, что сочетают в себе два этим традиционных метода.

Итак, наша гипотеза о том, что задачи оптимизации можно решить с помощью генетических алгоритмов нашла свое подтверждение.

В заключении, можно привести случаи, когда применение генетических алгоритмов не только возможно, но и является лучшим выбором.

Первый случай, когда не известен способ точного решения задачи. Если мы знаем, как оценить приспособленность хромосом, то всегда можем заставить генетический алгоритм решать эту задачу.

Второй случай: когда способ для точного решения существует, но он очень сложен в реализации, требует больших затрат времени и денег.

Что же касается недостатков, то в общем случае генетические алгоритмы не находят оптимального решения очень трудных задач. Если оптимальное решение задачи (например, задача коммивояжера с очень большим числом городов) не может быть найдено традиционными способами, то и генетический алгоритм вряд ли найдет оптимум.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Вентцель Е.С. «Исследование операций», - М.: 1972 г.

2. «Генетические алгоритмы: почему они работают?»/, «Компьютерра», № 11, 1999

3. «Генетические алгоритмы и машинное обучение»

http://www.math.tsu.ru/russian/ center/ai_group/ai_collection/docs/faqs/ai/part5/faq3.html

4. Исаев С. Популярно о генетических алгоритмах

www.algolist.manual.ru

5. «Нейропроект. Аналитические технологии XXI века» http://www.neuroproject.ru/genealg.php#what

6. Коршунов Ю.М. «Математические основы кибернетики. Для студентов вузов», - М.: 1987 г., стр. 67-89

7. «Лекции по нейронным сетям и генетическим алгоритмам»

http://infoart.baku.az/inews/300 00007.htm

8. Струнков Т. «Что такое генетические алгоритмы?» www.neuroproject.ru/papers.htm

9. Рутковская Д., Пилиньский М., Рутковский Л. «Нейронные сети, генетические алгоритмы и нечеткие системы»: Пер. с польск. И. Д. Рудинского. - М.: Горячая линия -Телеком, 2006. - 452 с: ил.

10. «Факультет вычислительной математики и кибернетики МГУ (ВМиК)»

http://cmc.cs.msu.su/labs/lvk/materials/tez_sapr99 _1.html

11. «(EHIPS) Генетические алгоритмы»

http://www.iki.rssi.ru/ehips/gene tic.htm

12. «Neural Bench Development»

http://www.neuralbench.ru/rus/theory/genetic.htm

13. «SENN Генетические Алгоритмы»

http://fdmhi .mega.ru/ru/senn_ga.htm

ПРИЛОЖЕНИЕ А

Программный код решения задачи коммивояжера с помощью генетических алгоритмов в BorlandDelphi 6.0

Const//объявляем константу

x=5;

var

Form1: TForm1;

town: array [1..21,1..25] of string; // объявляем массив городов

implementation

{$R *.dfm}

procedure TForm1.N3Click(Sender: TObject); // выводит сообщение о выходе

const

mbYesNo = [mbYes, mbNo];

begin

if MessageDlg('Выдействительнохотитевыйти?', mtConfirmation, mbYesNo, 0) = mrYes

then close;

end;

procedure TForm1.N2Click(Sender: TObject); // сообщение о программе

begin

ShowMessage('Демонстрация задачи коммивояжёра, решенной с помощью генетических алгоритмов. Дляучебногопособия "Генетическиеалгоритмы"!!!');

end;

procedure TForm1.Button1Click(Sender: TObject);

var i, j, k, a, b, s1, s2, p: integer;

begin

for i:=1 to x do

begin

StringGrid1.Cells[i,i]:='0'; //выводит в массиве «0» на пересечении [ i , i ]

for j:=1 to x do

StringGrid1.Cells[i,j]:=StringGrid1.Cells[j,i]; // расстояние [i, j]= [j, i]

еnd;

town[1,1]:='12345'; // создает начальную популяцию

a:=2; // выбор точки разрыва

for k:=1 to 4 do

begin // процедура скрещивания

town[1,a]:=town[1,a-1]; // выбираются особи из популяции

town[1,a][4]:=town[1,a-1][5]; // оператор кроссовера

town[1,a][5]:=town[1,a-1][4];

town[1,a+1]:=town[1,a-1]; // помещаем хромосому в новую популяцию

town[1,a+1][3]:=town[1,a-1][5]; // оператор кроссовера

town[1,a+1][5]:=town[1,a-1][3];

town[1,a+2]:=town[1,a+1]; // помещаем хромосому в новую популяцию

town[1,a+2][5]:=town[1,a+1][4]; // оператор кроссовера

town[1,a+2][4]:=town[1,a+1][5];

town[1,a+3]:=town[1,a+2]; // помещаем хромосому в новую популяцию

town[1,a+3][3]:=town[1,a+2][5]; // оператор кроссовера

town[1,a+3][5]:=town[1,a+2][3];

town[1,a+4]:=town[1,a+3]; // помещаем хромосому в новую популяцию

town[1,a+4][5]:=town[1,a+3][4]; // оператор кроссовера

town[1,a+4][4]:=town[1,a+3][5];

town[1,a+5]:=town[1,a+4]; // помещаем хромосому в новую популяцию

town[1,a+5][5]:=town[1,a+4][2]; // оператор кроссовера

town[1,a+5][2]:=town[1,a+4][5];

a:=a+6; // новая популяция всех допустимых решений

end;

a:=0; //нахождение оптимального решения, оценивание приспособленности каждой особи

s2:=9999999;

for i:=1 to 24 do

begin

s1:=0;

for p:=1 to x do

begin

a:=StrToInt(town[1,i][p]);

if p=5 then b:=StrToInt(town[1,i][p-4])

else b:=StrToInt(town[1,i][p+1]);

s1:=s1+StrToInt(StringGrid1.Cells[b,a]);

end;

if s1<s2 then

begin

s2:=s1;

town[2,1]:=town[1,i];

end;

end;

for i:=1 to 25 do

StringGrid2.Cells[1,i]:=town[1,i];

StringGrid2.Cells[2,1]:=IntToStr(s2);

Edit2.Text:=town[2,1]; //вывод оптимального решения

Edit1.Text:=IntToStr(s2); // вывод минимального расстояния

end;

procedure TForm1.Button3Click(Sender: TObject); // строим массив

var i,j: integer;

begin

StringGrid1.ColCount:=x+1;

StringGrid1.RowCount:=x+1;

StringGrid2.ColCount:=x+1;

StringGrid2.RowCount:=26;

fori:=1 toxdo// массив для начальной популяции

for j:=1 to x do

StringGrid1.Cells[i,j]:='' ''; //для ввода значений расстояний

fori:=1 toxdo

begin

StringGrid1.Cells[i,i]:='0';

StringGrid1.Cells[i,0]:=IntToStr(i);

StringGrid1.Cells[0,i]:=IntToStr(i);

StringGrid2.Cells[i,0]:=IntToStr(i);

end;

fori:=1 tox*2 do // массив для популяции нового поколения

StringGrid2.Cells[0,i]:=IntToStr(i);

end;

end.