| Скачать .docx |
Курсовая работа: Курсовая работа: Условия неопредел нности критерий Сэвиджа 2
Содержание
Введение
Теоретическиеосновыразрабатываемойтемы
1. Практическая часть
2.1 Математическая модель задачи
2.2 Аналитическое решение задачи
2.3 Компьютерный вариант решения задачи
2.3.1 Блок-схема решения задачи
2.3.2 Текст компьютерного решения задачи
2.3.3 Инструкция по использованию решения задачи
Заключение
Список литературы
Введение.
Проблемы выполнения различных вычислений была актуальна во все времена. По мере развития общественно-экономических отношений усложнялись поставленные задачи, которые для своего решения требовали разработки новых методов вычислений. На смену простейшим арифметическим и геометрическим вычислениям пришли алгебраические и тригонометрические вычисления.
Организация современного производства требует не только наличия современных станков и оборудования, но и разработки новых технологических процессов и современных методов управления производством. Для решения каждой из поставленных задач разрабатываются математические модели, анализируя которые, удаётся найти наилучшее решение поставленной задачи. Создание математической модели – сложная и кропотливая работа, которая в современных условиях под силу коллективам разработчиков.
Для создания математической модели одного и того же объекта различные коллективы могут использовать различный математический аппарат. В коллектив разработчиков математических моделей привлекаются высококвалифицированные специалисты, которые, с одной стороны, хорошо знают физические процессы, протекающие при работе объекта, и, с другой стороны, глубоко и всесторонне владеют соответствующим математическим аппаратом. После создания математической модели специалистами-аналитиками за дело принимаются специалисты-программисты, которые реализуют созданную модель в виде программных кодов. Далее с математической моделью работают специалисты-практики. Целенаправленно воздействуя на модель, они изучают её поведение и подбирают оптимальный режим работы для реального объекта.
Задача, даннаянакурсовуюразработку, относитсяктипузадач«Теорияигр», аточнее«принятиерешенийвусловияхнеопределённости».
Принять решение — это решить некоторую экстремальную задачу, т.е. найти экстремум некоторой функции, которую называют целевой , при некоторых ограничениях. Например, линейное программирование представляет целый класс таких экстремальных задач. Методы теории вероятностей и математической статистики помогают принимать решения в условиях неопределенности.
Не все случайное можно “измерить” вероятностью. Неопределенность — более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик, отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера. [4]
1 Теоретические основы разрабатываемой темы.
Как правило, большинство реальных инженерных задач содержит в том или ином виде неопределенность. Можно даже утверждать, что решение задач с учетом разного вида неопределенностей является общим случаем , а принятие решений без их учета - частным . Однако, из-за концептуальных и методических трудностей в настоящее время не существует единого методологического подхода к решению таких задач. Тем не менее, накоплено достаточно большое число методов формализации постановки и принятия решений с учетом неопределенностей. При использовании этих методов следует иметь в виду, что все они носят рекомендательный характер и выбор окончательного решения всегда остается за человеком. Руководитель, менеджер, обязан разрешать проблемы, встающие перед ним, перед коллективом, которым он руководит. Он обязан принимать решения. В теории принятия решений есть специальный термин: ЛПР — Лицо, Принимающее Решения. Ниже по тексту будем использовать этот термин [3].
Как уже указывалось, при решении конкретных задач с учетом неопределенностей ЛПР сталкивается с разными их типами. В исследовании операций принято различать три типа неопределенностей:
- неопределенность целей;
- неопределенность наших знаний об окружающей обстановке и действующих в данном явлении факторах (неопределенность природы);
- неопределенность действий активного или пассивного партнера или противника.
В приведенной выше классификации тип неопределенностей рассматривается с позиций того или иного элемента математической модели. Так, например, неопределенность целей отражается при постановке задачи на выборе либо отдельных критериев, либо всего вектора полезного эффекта.
С другой стороны, два другие типа неопределенностей влияют, в основном, на составление целевой функции уравнений ограничений и метода принятия решения. Конечно, приведенное выше утверждение является достаточно условным, как, впрочем, и любая классификация. Мы приводим его лишь с целью выделить еще некоторые особенности неопределенностей, которые надо иметь в виду в процессе принятия решений.
Неопределенные факторы, закон распределения которых неизвестен, являются наиболее характерными при исследовании качества адаптивных систем. Именно на этот случай следует ориентироваться при выборе гибких конструкторских решений. Методический учет таких факторов базируется на формировании специальных критериев, на основе которых принимаются решения. Критерии Вальда, Сэвиджа, Гурвица и Лапласа уже давно и прочно вошли в теорию принятия решений.
В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации:
![]()
(1.1)
Здесь величину W можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Vj вместоварианта Ui выбрать другой, оптимальный для этого внешнего состояния, вариант.
Соответствующее критерию Сэвиджа правило выбора следующее: каждый элемент матрицы решений [Wij ] вычитается из наибольшего результата max Wij соответствующего столбца. Разности образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей Wir . Выбирается тот вариант, в строке которого стоит наименьшее значение [2].
Пример : Обоснование состава ремонтной бригады.
На предприятии решается вопрос о создании ремонтной бригады. Основываясь на применении критерия Сэвиджа, определить наиболее целесообразное число членов бригады. Исходные данные сведены в таблице (1.1), в ячейках которой занесены доходы при разных вариантах (стратегиях). Под стратегией понимается x -число членов бригады и R - количество станков, требующих ремонта.
Таблица 1.1
| x\R | 40 | 30 | 20 | 10 |
| 5 | 50 | 100 | 180 | 250 |
| 4 | 80 | 70 | 80 | 230 |
| 3 | 210 | 180 | 120 | 210 |
| 2 | 300 | 220 | 190 | 150 |
В этом случае составляется новая матрица, элементы которой составляются по правилу:
 (1.2)
(1.2)
Составим матрицу W(xi , Rj ) - матрицу сожалений для случая, когда uij - потери, используя предыдущие данные. Соответствующая матрица (1.2) получается путем вычисления значений min(xi , Rj ), равных 50, 70, 80 и 150 из столбцов 1, 2, 3, 4, соответственно
Таблица 1.2
| max W(xi , Rj ) | |||||
| 0 | 30 | 100 | 100 | 100 | |
| W(xi ,Rj )= | 30 | 0 | 0 | 0 | 30 |
| 160 | 110 | 40 | 60 | 160 | |
| 250 | 150 | 110 | 0 | 250 |
Таким образом, минимальные потери будут при x=2, когда max W(xi , Rj )=30.
Общие рекомендации по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. [1]
2 Практическая часть.
2.1 Математическая модель задачи.
Исходя из условия задачи, была составлена математическая модель, где была разработана табличная структура задачи табл.(2.1). Определить оптимальный минимальный доход (по критерию Сэвиджа) за день.
Первоначально, случайным образом, в таблицу заносится количество людей, купивших определённый товар в определённый день табл.(2.1).
Таблица 2.1
| Дни | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| День 1 | 1 | 4 | 87 | 21 |
| День 2 | 28 | 68 | 32 | 17 |
| День 3 | 38 | 43 | 9 | 48 |
| День 4 | 8 | 85 | 6 | 30 |
2.2 Аналитическое решение задачи.
Используя таблицу (2.1) и цены на товары
Присвоим табличные данные (2.1) матрице Z. Согласно критерию Сэвиджа Z=min(max(Zij-minZij)), i-день, j-товар, нужно составить новую матрицу, матрицу рисков. Для этого сначала найдём minZ, путём выбора в таблице по столбцам наибольших чисел.
Воспользуясь данными таблицы (2.1) найдём доход за каждый день на каждый товар, с помощью перемножения цены на товар. Цены: одежда - 1, обувь - 2, книги - 3, игрушки - 4. Смотрите таблицу (2.2).
Таблица 2.2
| Дни | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| День 1 | 1 | 8 | 261 | 84 |
| День 2 | 28 | 136 | 96 | 68 |
| День 3 | 38 | 86 | 27 | 192 |
| День 4 | 8 | 170 | 18 | 120 |
Таблица 2.3
| minZ | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| 1 | 8 | 18 | 68 | |
Далее надо найти матрицу, путем вычитания (Zij-minZij), где С1- одежда, С2 – обувь, С3 – книги, С4 - игрушки .
Таблица 2.4
| Дни | Ассортимент товара | |||
| С1 | С2 | С3 | С4 | |
| День 1 | 0 | 0 | 243 | 16 |
| День 2 | 27 | 128 | 78 | 0 |
| День 3 | 37 | 78 | 9 | 124 |
| День 4 | 7 | 162 | 0 | 52 |
Следуя формуле, найдём max(Zij-minZij), выбирая из каждого столбца таблицы (2.4) максимальное число. Отразим это в таблице (2.5).
Таблица 2.5
| max | Ассортимент товара | |||
| одежда | обувь | книги | игрушки | |
| 37 | 162 | 243 | 124 | |
И, наконец, найдём оптимальный минимальный доход, выбрав минимальное число из таблицы (2.5).
Этим числом является 37. Смотрим таблицу (2.5) чтобы найти его расположение. Оно находится в столбце “одежда” и строке “День 3”.
Ответ: оптимальный минимальный доход (по критерию Сэвиджа) равен 37 за 3 день.
2.3 Компьютерный вариант решения задачи.
![]() 2.3.1 Блок-схема решения задачи.
2.3.1 Блок-схема решения задачи.
|

![]()



 |
 |
 |
|
|
|

|



|

|
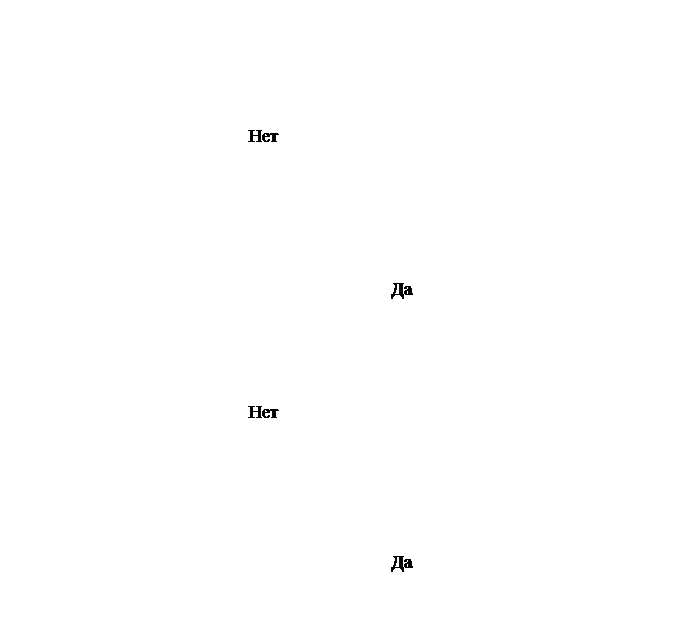
2.3.2 Текст компьютерного решения задачи.
Programkurs9k;
uses crt;
type armarka=record
c1:real; {odezda }
c2:real; {obyv }
c3:real; {knigi }
c4:real; {igryshki }
end;
var
a:array [1..4] of armarka;
n1,n2,n3,n4:real; {chisla dlya min (minZij) }
codezda, cobyv, cknigi, cigryshki:real; {ceni za tovar }
b:array[1..4] of armarka;
i:integer;
z:integer; {dni}
r1,r2,r3,r4:real; {chisla dlya max (max b[i])}
min:real;
{shapka }
procedure shapka;
begin
writeln('___________________________________________________');
writeln('| | tovar | Zij - minZij |');
writeln('| |___________________________|__________________|');
writeln('| den | odezda | obyv | knigi |igryshki| c1 | c2 | c3 | c4 |');
writeln('|_____|______|_______|_____|_______|____|_____|____|____|');
end;
{vvod cen na tovar }
begin
writeLn('vvedite ceny na odezgy ');
readln(codezda);
writeLn('vvedite ceny na obyv ');
readln(cobyv);
writeLn('vvedite ceny na knigi ');
readln(cknigi);
writeLn('vvedite ceny na igryshki ');
readln(cigryshki);
{naxogdenie cluchainim obrazom pokupateley }
for i:=1 to 4 do
begin
a[i].c1:=random(100)+1;
a[i].c2:=random(100)+1;
a[i].c3:=random(100)+1;
a[i].c4:=random(100)+1;
end;
{podshet cen- pokupateli*ctovara }
for i:=1 to 4 do
begin
a[i].c1:= a[i].c1*codezda;
a[i].c2:= a[i].c2*cobyv;
a[i].c3:= a[i].c3*cknigi;
a[i].c4:= a[i].c4*cigryshki;
end;
{naxogdenie min v kagdom stolbce }
n1:=a[1].c1;
for i:=1 to 4 do
begin
if n1>a[i+1].c1 then
n1:=a[i+1].c1;
end;
n2:=a[1].c2;
for i:=1 to 4 do
begin
if n2>a[i+1].c2 then
n2:=a[i+1].c2;
end;
n3:=a[1].c3;
for i:=1 to 4 do
begin
if n3>a[i+1].c3 then
n3:=a[i+1].c3;
end;
n4:=a[1].c4;
for i:=1 to 4 do
begin
if n4>a[i+1].c4 then
n4:=a[i+1].c4;
end;
{nahogdenie (zij-minzij) }
writeln;
for i:=1 to 4 do
begin
b[i].c1:=a[i].c1-n1;
b[i].c2:=a[i].c2-n2;
b[i].c3:=a[i].c3-n3;
b[i].c4:=a[i].c4-n4;
end;
r1:=b[1].c1;
for i:=1 to 4 do
begin
if r1<b[i+1].c1 then
r1:=b[i+1].c1;
end;
r2:=b[1].c2;
for i:=1 to 4 do
begin
if r2<b[i+1].c2 then r2:=b[i+1].c2;
end;
r3:=b[1].c3;
for i:=1 to 4 do
begin
if r3<b[i+1].c3 then r3:=b[i+1].c3;
end;
r4:=b[1].c4;
for i:=1 to 4 do
begin
if r4<b[i+1].c4 then r4:=b[i+1].c4;
end;
{nahogdenie otveta }
min:=r1;
z:=1;
if min> r2 then
begin
min:=r2;
z:=2;
end;
if min> r3 then
begin
min:=r3;
z:=3;
end;
if min> r4 then
begin
min:=r4;
z:=4;
end;
shapka;
{vivod podschitannogo }
for i:=1 to 4 do
begin
writeln('| day ',i:1 ,'|',a[i].c1:8:2,'|',a[i].c2:8:2,'|',a[i].c3:8:2,'|',a[i].c4:8:2,'|',
b[i].c1:7:2,'|',b[i].c2:7:2,'|',b[i].c3:7:2,'|',b[i].c4:7:2,'|' );
writeln('|_________________________________________________________________|');
end;
writeln;
writeln;
writeln(' ________________________________________________________________ ');
writeln('| |') ;
writeln('|Max(Zij-minZij):|', r1:13:2,'| ',r2:13:2,'| ',r3:13:2,'| ',r4:13:2,'|' );
writeln('|_________________________________________________________________|');
writeln;
writeln('Otvet:Optimalni variant (po kriteriu Sevidga) coctavliyaet za 3 den s zna4eniem ', min:7:2);
readln ;
repeat until keypressed;
readln;
end.
{konec }
2.3.2. Инструкция по использованию решения задачи.
Во время запроса нужно ввести цены на товар (1)
Рисунок 1

После появляется посчитанная таблица (2), в которой, в графе tovar указана начальная матрица прибыли, а в графе Zij - minZijуказана матрица рисков. В нижней строчке под таблицей указан Max(Zij-minZij). На последней строчке показан ответ решения задачи.
Рисунок 2

Заключение.
Внедрение компьютеров в данную область науки привело к ускорению и упрощению расчетов, что высоко цениться у работников, производивших ранее эти расчёты в ручную. Это не только экономия времени и сил, но и точность ответа, т.к. компьютер никогда не ошибается.
На рис. 2 представлен результат работы программы на TurboPascal. Данный результат совпал с аналитическим решениемзадачи.
Список литературы.
1. Андреев В.Н., Герасимов Ю.Ю. Принятие оптимальных решений: Теория и применение в лесном деле. Йоэнсуу: Из-во ун-та Йоэнсуу, 1999. 200 с.
2. Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. М.: Наука, 1969. 120 с.
3. Вентцель Е.С. Элементы динамического программирования. М.: Наука, 1964. 176 с.
4. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Наука, 1988.
5. Юдин Д.Б. Задачи и методы стохастического программирования. М.: Сов. радио, 1979. 392 с.
6. Davis L.S., Johnson K.N. Forest management. New York: McGraw-Hill Book Company, 1987. 790 p.
7. Моисеев Н.Н., Математические методы системного анализа М. Наука 1981 487 с.