| Скачать .docx |
Дипломная работа: Дипломная работа: Обработка изображений на основе аналоговых нейрокомпьютеров
Федеральное агентство по образованию РФ
Курский государственный технический университет
Кафедра ВТ
ОБРАБОТКА ИЗОБРАЖЕНИЙ НА ОСНОВЫ АНАЛОГОВЫХ НЕЙРОКОМПЬЮТЕРОВ
Курск – 2009
Содержание
1 Общие сведения о нейрокомпьютерах. 5
1.1 Что такое нейрокомпьютер. 5
1.2 История нейрокомпьютеров. 7
1.3 Современный нейрокомпьютер. 10
1.5 Особенности архитектуры аналоговых и гибридных ЭВМ. 13
1.5.1 Основные методы неалгоритмических вычислений. 13
2 Компьютерной обработки изображений. 22
2.1 Определение компьютерной обработки изображений. 22
2.2 Устройства формирования изображений. 24
2.2 Пространственные спектры изображений. 29
2.3 Спектральные интенсивности изображений. 31
2.4 Вероятностные модели изображений и функции Автокорреляции. 32
2.5 Критерии качества изображений. 33
Список используемой литературы: 39
Введение
Несмотря на то, что нейронные сети как научно-технический объект существуют более полувека, основные способы их практической реализации ограничиваются областью программного моделирования в различных средах визуального (и не визуального) проектирования. Программные реализации преобладают над аппаратными. Кроме того, аппаратные реализации вследствие своей относительной дороговизны до сих пор не имеют повсеместного распространения. Однако их удельный вес в общем количестве мировых технологических разработок неуклонно растет. Впереди планеты всей в данном направлении, как всегда, шагает Япония, где разработки на основе нейросетевых технологий успешно внедряются во множестве образцов бытовой техники, таких как фотоаппараты, микроволновые печи, видеокамеры и т.д. Не отстают и другие развитые страны.
Обработка изображений – одно из интенсивно развиваемых направлений исследования. Однако, обработка изображений на основы аналоговых нейрокомпьютеров все еще относительно новое направление.
Таким образом, актуальной научно-технической задачей является обработка изображения с помощью аналоговых устройств.
Цель диссертации : разработка алгоритмов и схем аналоговых нейрокомпьютеров для выполнения разных задач обработки изображений.
Задачи исследований:
1. Сравнительный анализ методов обработки изображений, используемых для устройств с аналоговой обработкой изображения
2. Аналитический обзор устройств с аналоговой обработкой изображений
3. Анализ цифровой и аналоговой реализации алгоритмов обработки изображений с использованием нейронных сетей
4. Разработка математической модели устройства аналоговой обработки изображений
5. Разработка аппаратно-ориентированных алгоритмов предварительной обработки изображений
6. Моделирование разработанных алгоритмов и устройств
1. Общие сведения о нейрокомпьютерах
1.1 Что такое нейрокомпьютер
Нейрокомпьютеры – это системы, в которых алгоритм решения задачи представлен логической сетью элементов частного вида – нейронов с полным отказом от булевских элементов типа И, ИЛИ, НЕ. Как следствие этого введены специфические связи между элементами, которые являются предметом отдельного рассмотрения. В отличие от классических методов решения задач нейрокомпьютеры реализуют алгоритмы решения задач, представленные в виде нейронных сетей. Это ограничение позволяет разрабатывать алгоритмы, потенциально более параллельные, чем любая другая их физическая реализация.
Нейросетевая тематика является междисциплинарной, что обусловило значительные разночтения в общих терминологических подходах. Нейросетевой тематикой занимаются как разработчики вычислительных систем и программисты, так и специалисты в области медицины, финансово-экономические работники, химики, физики и т.п. (т.е. все кому не лень). То, что понятно физику, совершенно не принимается медиком и наоборот – все это породило многочисленные споры и целые терминологические войны по различным направлениям применения всего где есть приставка нейро –.
Приведем некоторые наиболее устоявшиеся определения нейрокомпьютера
| № |
Научное направление |
Определение нейровычислительной системы |
| 1 |
Математическая статистика |
Нейрокомпьютер – это вычислительная система автоматически формирующая описание характеристик случайных процессов или их совокупности, имеющих сложные, зачастую многомодальные или вообще априори неизвестные функции распределения. |
| 2 |
Математическая логика |
Нейрокомпьютер – это вычислительная система алгоритм работы которой представлен логической сетью элементов частного вида – нейронов, с полным отказом от булевых элементов типа И, ИЛИ, НЕ. |
| 3 |
Пороговая логика |
Нейрокомпьютер – это вычислительная система, алгоритм решения задач в которой представлен в виде сети пороговых элементов с динамически перестраиваемыми коэффициентами и алгоритмами настройки, независимыми от размерности сети пороговых элементов и их входного пространства |
| 4. |
Вычислительная техника |
Нейрокомпьютер – это вычислительная система с MSIMD архитектурой, в которой процессорный элемент однородной структуры упрощен до уровня нейрона, резко усложнены связи между элементами и программирование перенесено на изменение весовых коэффициентов связей между процессорными элементами. |
| 5. |
Медицина (нейробиологический подход) |
Нейрокомпьютер – это вычислительная система представляющая собой модель взаимодействия клеточного ядра, аксонов и дендридов, связанных синаптическими связями (синапсами) (т.е. модель биохимических процессов протекающих в нервных тканях). |
| 6. |
Экономика и финансы |
Устоявшегося определения нет, но чаще всего под нейровычислителем понимают систему обеспечивающую параллельное выполнение «бизнес» – транзакций. |
В дальнейшем под нейрокомпьютером будем понимать вычислительную систему с архитектурой MSIMD, в которой реализованы два принципиальных технических решения: упрощен до уровня нейрона процессорный элемент однородной структуры и резко усложнены связи между элементами; программирование вычислительной структуры перенесено на изменение весовых связей между процессорными элементами.
Общее определение нейрокомпьютера может быть представлено в следующем виде:
Нейрокомпьютер – это вычислительная система с архитектурой аппаратного и программного обеспечения, адекватной выполнению алгоритмов, представленных в нейросетевом логическом базисе
Преимущества нейрокомпьютеров.
По сравнению с обычными компьютерами нейрокомпьютеры обладают рядом преимуществ.
Во-первых – высокое быстродействие, связанное с тем, что алгоритмы нейроинформатики обладают высокой степенью параллельности.
Во-вторых – нейросистемы делаются очень устойчивыми к помехам и разрушениям.
В третьих – устойчивые и надежные нейросистемы могут создаваться из ненадежных элементов, имеющих значительный разброс параметров.
Несмотря на перечисленные выше преимущества эти устройства имеют ряд недостатков:
1. Они создаются специально для решения конкретных задач, связанных с нелинейной логикой и теорией самоорганизации. Решение таких задач на обычных компьютерах возможно только численными методами.
2. В силу своей уникальности эти устройства достаточно дорогостоящи.
1.2 История нейрокомпьютеров
Нейрокомпьютеры – это ЭВМ нового поколения, качественно отличающиеся от других классов вычислительных систем параллельного типа тем, что для решения задач они используют не заранее разработанные алгоритмы, а специальным образом подобранные примеры, на которых учатся. Их появление обусловлено объективными причинами: развитие элементной базы, позволяющее на одной плате реализовать персональный компьютер – полнофункциональный компьютер (модель нейрона), и необходимость решения важных практических задач, поставленных действительностью. Попытки создания ЭВМ, моделирующих работу мозга, предпринимались ещё в 40-х гг. специалистами по нейронной кибернетике. Они стремились разработать самоорганизующиеся системы, способные обучаться интеллектуальному поведению в процессе взаимодействия с окружающим миром, причём компонентами их систем обычно являлись модели нервных клеток. Однако зарождавшаяся в это же время вычислительная техника и связанные с нею науки, особенно математическая логика и теория автоматов, оказали сильное влияние на области исследования, связанные с мозгом.
К концу 50-х гг. сформировался логико-символьный подход к моделированию интеллекта. Его развитие создало такие направления, как эвристическое программирование и машинный интеллект, и способствовало угасанию интереса к нейронным сетям. К началу 80-х гг. были созданы условия для возрождения интереса к нейросетевым моделям. Это было связано с накоплением новых данных при экспериментальных исследованиях мозга.
К настоящему времени сформировался обширный рынок нейросетевых продуктов. Подавляющее большинство продуктов представлено в виде моделирующего программного обеспечения. Ведущие фирмы разрабатывают также и специализированные нейрочипы или нейроплаты в виде приставок персональным ЭВМ. Наиболее ярким прототипом супернейрокомпьютера является система обработки аэрокосмических изображений, разработанная в США по программе «Силиконовый мозг». Объявленная производительность супернейрокомпьютера составляет 80 PFLOPS (80∙1015 операций с плавающей точкой в 1 с) при физическом объёме, равном объёму человеческого мозга, и потребляемой мощности 20 Вт.
В июле 1992 г. в Японии была принята Пятая Программа (действующая и поныне), связанная с созданием координационного исследовательского центра по реализации международного проекта Real World Computing Partnership (RWCP), основной целью которого являлась разработка практических методов решения реальных задач на основе гибких и перспективных информационных технологий.
В настоящее время в рамках развития этого проекта создана трансконтинентальная сеть на базе гетерогенной вычислительной среды, объединяющей Суперкомпьютерный центр в Штутгарте (Германия), Компьютерный центр в Питсбурге (шт. Пенсильвания), Электротехническую лабораторию в Тшукубе (Япония), Компьютерный центр в Манчестере (Великобритания), в которой часть пользовательских компьютеров выполнена по нейросетевой технологии. Пиковая производительность образованного сверхсуперкомпьютера составила 2.2 TFLOPS.
Считается, что теория нейронных сетей, как научное направление, впервые была обозначена в классической работе МакКаллока и Питтса[1] 1943 г., в которой утверждалось, что, в принципе, любую арифметическую или логическую функцию можно реализовать с помощью простой нейронной сети. В 1958 г. Фрэнк Розенблатт [2] придумал нейронную сеть, названную перцептроном, и построил первый нейрокомпьютер Марк‑1. Перцептрон был предназначен для классификации объектов. На этапе обучения «учитель» сообщает перцептрону к какому классу принадлежит предъявленный объект. Обученный перцептрон способен классифицировать объекты, в том числе не использовавшиеся при обучении, делая при этом очень мало ошибок. Примерно в это же время вышла работа Минского и Пейперта[3], указавшая ограниченные возможности простейшего перцептрона. Результаты Минского и Пейперта погасили энтузиазм большинства исследователей, особенно тех, кто работал в области вычислительных наук.
С начала 80‑х годов ИНС вновь привлекли интерес исследователей, что связано с энергетическим подходом Хопфилда[4] и алгоритмом обратного распространения для обучения многослойного перцептрона (многослойные сети прямого распространения), впервые предложенного Вербосом[5]. При этом важную роль сыграли работы группы PDP (Parallel Distributed Processing). В них рассматривались нейронные сети, названные многослойными перцептронами, которые оказались весьма эффективными для решения задач распознавания, управления и предсказания. (Многослойные перцептроны занимают ведущее положение, как по разнообразию возможностей использования, так и по количеству успешно решенных прикладных задач.)
1.3 Современный нейрокомпьютер
Сейчас количество проданных в странах Запада нейрокомпьютеров исчисляется десятками тысяч. В основном это нейрокомпьютерные программы для ПЭВМ, предназначенные для решения задач аппроксимации и прогнозирования числовых данных. Около 5% нейрокомпьютеров относятся к устройствам профессионального уровня, ориентированным на применение мощных рабочихстанций и аппаратных нейроакселераторов. Программное обеспечение таких систем обычно содержит библиотеки нейропарадигм, что позволяет при решении задач использовать различные типы нейронных сетей. Типичным примером может служить система BrainMaker фирмы CSS (США), получившая в 1990 г. приз журнала PC Magazine «Лучший программный продукт года». Система может работать на любом компьютере, на котором установлен Windows. Базовая версия (цена 950 долларов) ориентирована на широкий круг пользователей. Ее применение не требует специальных знаний. Настройка сети ограничена установкой нескольких параметров, главным среди которых является допустимая погрешность ответа. Основная работа состоит в подготовке данных для обучения, которые можно импортировать из файлов формата *.DBF, *.TXT, Excel, Lotus 1–2–3. При удачном подборе примеров система дает 95% правильных ответов.
Для расширения возможностей системы служит набор дополнительных программ Toolkit Option, позволяющих ускорить процесс обучения и улучшить представление графических данных. Для профессиональных пользователей выпускается расширенная версия BrainMaker Professional, позволяющая моделировать сети с числом нейронов до 8192 (допускается расширение до 37767), цена которой составляет 1550 долларов. Для этой версии создан набор дополнительных программных средств, которые включают Genetic Training Option – программу оптимизации, использующую «генетические» алгоритмы, и Training Finansial Data – специальные наборы данных для настройки нейронной сети на коммерческие приложения.
Наконец, для наиболее крупных приложений выпущен BrainMaker Accelerator – специализированная нейроплата – акселератор на базе сигнального процессора TMS320C25 фирмы Texas Ins., позволяющая в несколько раз повысить производительность нейрообработки данных. Еще более мощная версия аппаратного расширителя BrainMaker Accelerator Pro, содержащая пять процессоровTMS320C25 и до 32 Мбайт оперативной памяти, позволяет ускорить процесс обучения в сорок раз по сравнению с компьютером PC 486DX‑50.
1.4 Нейрочипы
Алгоритм, заданный нейронной сетью, может быть интерпретирован обычной универсальной вычислительной машиной, либо некоторым специализированным устройством [5].
Построение вычислительных систем, интерпретирующих нейросетевые алгоритмы, осуществляется сейчас на традиционной элементной базе. Однако весьма многообещающей выглядит потенциальная возможность реализации базисной операции (вычисления скалярного произведения) в физической среде-носителе сигнала. Прежде всего, это касается операции суммирования в электромагнитном поле, хотя в живых организмах существуют и иные примеры, в частности, суммирования на биохимическом уровне. Реализация скалярного произведения за счет суммирования электромагнитного поля (включая оптический диапазон) может привести к тому, что время срабатывания элемента, вычисляющего скалярное произведение, будет исключительно малым, сравнимым со временем прохождения светом линейного размера элемента.
Одним из первых коммерчески доступных нейрочипов был Micro Devices MD1220 (1990 год) [6]. Этот кристалл интерпретирует 8 нейронов и 8 связей с 16‑ти разрядными, хранящимися во внутрикристальной памяти, весами и одноразрядными входами. Входы имеют одноразрядные последовательные умножители. Сумматоры в кристалле также 16‑разрядные. Из этих нейрочипов путём их каскадирования могут быть построены нейрокомпьютеры.
Фирма Neuralogix производит нейрочип NLX – 420 с 16‑ти процессорными элементами, каждый из которых имеет 32‑х разрядный сумматор [7].
Фирма Hitachi выпустила Wafer Scale Integration – многокристальные полупроводниковые пластины [8]. На пластине размещается сеть Хопфилда с 576 нейронами, каждый из которых имеет 64 восьмиразрядных весовых коэффициента. Сеть Хопфилда функционирует как ассоциативная память. При подаче на входы частичной или ошибочной входной последовательности сеть через какое-то время переходит в одно из устойчивых состояний, предусмотренных при её конструировании. При этом на входах сети появляется последовательность, признаваемая сетью как наиболее близкая к одной из изначально поданных.
Помимо цифровых, бывают нейрочипы аналоговые и гибридные. Аналоговые элементы меньше и проще цифровых. Однако обеспечение необходимой точности требует тщательного проектирования и изготовления. Пример аналогового нейрочипа – Intel 80170NW ETANN. Этот кристалл содержит 64 нейрона и два банка 64x80 весов [9]. Гибридные нейрочипы используют комбинацию аналогового и цифрового подходов. Например, входы могут быть аналоговыми, веса загружаться как цифровые и выходы быть цифровыми. Чип CLNN‑32 фирмы Bellcore содержит 32 нейрона. Входы, выходы и внутренняя обработка – аналоговые, а 5‑ти разрядные веса цифровые [10].
В качестве нейропроцессоров иногда используются также сигнальные микропроцессоры. Разработанный в НТЦ «Модуль» российский нейпроцессор NM6403 (Neuro Matrix) имеет скалярное RISC‑ядро для выполнения логических операций, целочисленных арифметических операций, операций сдвига и формирования адресов для обращения в память, а также векторный процессор VP для обработки двоичных векторов произвольной разрядности в пределах 1–64 битов [11]. При этом в одном такте VP может выполнять операции над несколькими векторами, вплоть до 64, суммарная длина которых не превышает 64. Скалярный процессор выполняет всю подготовку данных для работы векторного процессора. Нейропроцессор NM6403 имеет два встроенных линка, совместимых по логическому и физическому протоколам с линками сигнального микропроцессора TMS 320 C4X.
1.5 Особенности архитектуры аналоговых и гибридных ЭВМ
1.5.1 Основные методы неалгоритмических вычислений
Один из путей повышения производительности ВС – применение параллельных неалгоритмических вычислений, основанных на непрерывной (аналоговой) форме представления (НФП) обрабатываемых математических величин:
Хмаш(tm)=mxXm(mtt),
Где Хмин, tm – машинные величины зависимой переменной и ее аргумента;
mх, mt – массштабы переменной Х и аргумента t.
НФП – это представление каждого мгновенного значения математической величины пропорциональным ему мгновенным значением машинной переменной. Погрешность D НФП определяется классом точности изготовления и стабильностью электрических элементов и электронных компонентов, с помощью которых реализуются машинные переменные, и проявляется при обратном преобразовании машинных величин в искомые математические величины:
XM(t)=(1/mX) Xмаш (tM/mt)+ D/mX,
Где D – абсолютная погрешность вычислений.
НФП позволяет реализовать неалгоритмический принцип вычислений (НПВ) путем ввода в машину и реализации решения задачи в общепринятой аналитической форме ее описания. Аналитический принцип обработки информации состоит в том, что каждой аналитической завимости между математическими переменными исходной задачи (интегродифференциальной, алгебраической, тригонометрической и т.п.) в машине соответствуют аналогичное (подобное) аналитическое описание связи между машинными переменными. Это достигается методом моделирования на основе теории подобия.
Наиболее распространенный НПВ – аналоговое математическое моделирование по методу непрямой аналогии, основанному на операционно-блочном построении модели, когда каждой операции и функции уравнений исходного оригинала в модели соответствует подобный операционный блок (сумматор, интегратор, блок умножения и деления, функциональный преобразователь и т.п.). Используя достаточный набор типовых операционных блоков, можно решать широкий класс математических задач. Программирование аналоговых вычислительных машин (АВМ) заключается в составлении схемы аналоговой модели, представляющей собой схему соединения друг с другом типовых операционных блоков в соответствии с заданной задачей, и в расчете настраиваемых параметров операционных блоков, так называемом масштабировании модели.
Например, нелинейное неоднородное обыкновенное дифуравнение второго порядка:
![]()
при начальных условиях: ![]()
может быть запрограммировано к решению на АВМ следующим способом.
Схема аналоговой модели составляется методом понижения порядка (выделением высшей производной и последовательным её интегрированием) и методом неявных функций, условно полагая искомые ![]() якобы вначале известными:
якобы вначале известными:
![]()
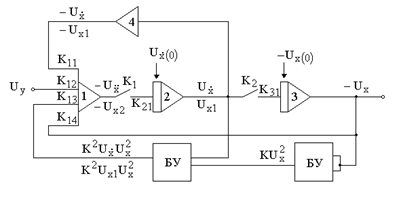
Блок 1 – аналоговый сумматор со стандартным оператором:
![]()
Блок 4 – инвертор с оператором: ![]() .
.
Блоки 2,3 – аналоговые интеграторы со стандартным оператором:
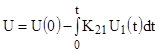 .
.
Блок БУ – аналоговый блок умножения с оператором: ![]() , где
, где
k – коэффициент нормирования шкалы выходного напряжения:
![]() ,
,
а ![]() - предельное значение шкалы на выходе операционного блока (
- предельное значение шкалы на выходе операционного блока (![]() в АВМ типа МН – 7).
в АВМ типа МН – 7).
Решение дифференциального уравнения начинается в момент времени t=0 синхронного замыкания пусковых ключей К1, К2 на входах интеграторов и завершается по окончании переходных процессов. Следовательно, в процессе вычислений все операционные блоки модели функционируют параллельно и одновременно. Этим и объясняется возможность повышения производительности на основе НПВ.
В исходном состоянии модели при разомкнутых ключах К1, К2 выполняется подготовка АВМ: ввод значений коэффициентов передачи (КП) К11,…, К14, К21, К31 и начальных условий, соединение операционных блоков по схеме модели.
Масштабирование модели состоит в расчете КП: К11,…, К14, К21, К31; НУ: ![]() и машинной переменной правой части Uy с учетом масштабов переменных. Оно заключается в выводе масштабных уравнений модели на основе сопоставления сходственных систем уравнений оригинала и модели.
и машинной переменной правой части Uy с учетом масштабов переменных. Оно заключается в выводе масштабных уравнений модели на основе сопоставления сходственных систем уравнений оригинала и модели.
Уравнения оригинала со вспомогательными переменными х1, х2 и обязательной нормировкой величины коэффициентов в левой части уравнений К=1:
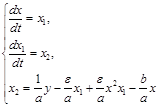
Уравнения модели как совокупность стандартных операторов операционных блоков (при выводе масштабных уравнений начальные значения интегралов вначале не учитываются.):
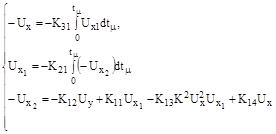
Уравнения модели, преобразованные в сходственную с оригиналом дифференциальную форму:
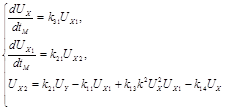
Уравнения модели, преобразованные путем замены машинных величин на математические величины оригинала с учетом их масштабов:
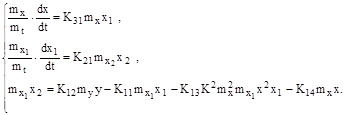
где 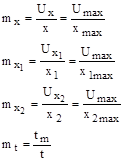
Нормированные уравнения модели:
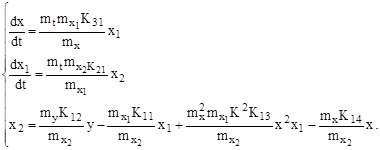
Масштабные уравнения модели, полученные путем сопоставления коэффициентов в одноименных членах нормированных уравнений модели и оригинала в соответствии с необходимостью тождественности сходственных уравнений модели и оригинала:
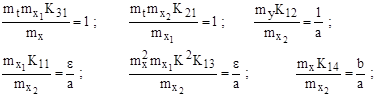
из которых однозначно находятся требуемые величины КП операционных блоков модели.
Масштабные соотношения НУ и правых частей:
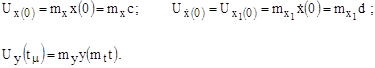
Основной недостаток данного типа НПВ – сравнительно большая погрешность решения задач, которая даже при относительной погрешности операционных блоков, построенных, как известно из схемотехники, на прецизионных резисторах и конденсаторах и операционных усилителях с очень большим коэффициентом усиления КУ=105…107, равной dОБЛ=100D/Umax=0,01…0,1%, достигает dмодели»1…5% из-за накоплений их погрешностей в сложных схемах аналоговых моделей.
Точность неалгоритмических вычислений повышают путем частичного или полного перехода от аналогового к цифровому моделированию, сохраняя основные преимущества НПВ – параллельное функционирование операционных блоков в вычислительном процессе. Применяются два основных подхода:
Реализация операционных блоков на цифровой схемотехнической элементной базе;
Распределение с учетом допустимой погрешности вычислений частей сложной задачи между аналоговым и цифровым процессорами.
ЭВМ, построенные с использованием сочетания аналогового и цифрового НПВ, т.е. аналогового и цифрового моделирования, называется гибридными вычислительными машинами (ГВМ), а ВС, представляющие собой комплекс ЦВМ и АВМ, объединенных с помощью ЦАП и АЦП, – гибридными (аналого-цифровыми) вычислительными комплексами (ГВК или АЦВК).
Следовательно, к НПВ, кроме аналогового математического моделирования, относятся:
· Цифровое моделирование (конечно-разностное и разрядное моделирование);
· Аналого-цифровое моделирование (частичное использование с целью повышения производительности параллельного НПВ в аналоговой части);
· Цифровой НПВ на основе неалгоритмического потокового программирования по степени готовности операндов, а не последовательности команд, как это принято в традиционно-абстрактной модели ЦВМ фон-Неймана.
Последний НПВ позволяет использовать для повышения производительности естественный параллелизм операций, имеющийся в большинстве решаемых задач. Однако он реализуется на основе особой функциональной и структурной организации цифрового процессора и особого машинного языка низкого уровня, отличающегося от ассемблера ЦВМ фон-Неймана, оставаясь по основным чертам абстрактной модели цифровой машиной, и поэтому к ГВМ не относится. ЭВМ этого типа организации принято называть потоковыми ЦВМ.
Особое место среди ГВМ занимают получившие весьма широкое распространение цифровые процессоры сигналов. В них не используется НПВ, а к ГВМ они относятся потому, что на входном и выходном их портах ввода-вывода дополнительно подключаются входной АЦП и выходной ЦАП, позволяющие по цифровым алгоритмическим программам обрабатывать аналоговые сигналы после их квантования по времени и по уровню. В настоящее время они успешно вытесняют сложную и недостаточно стабильную и технологичную преобразующую и вычислительную аналоговую схемотехнику. Однако для того, чтобы они с достаточной точностью обрабатывали широкополосные аналоговые сигналы (диапазон частот спектральных составляющих от 1 до 10 МГц) предъявляются очень высокие требования, как к быстродействию их элементной базы, так и производительности процессора. В них применяются сверхпараллельные функциональные узлы АЛУ, например однотактные матричные блоки умножения, однотактные параллельные двигатели и особая конвейерная организация структуры АЛУ и т.п. Со всеми этими методами организации, позволяющими повысить производительность, мы ознакомимся в этой дисциплине. Начнем с особенностей организации ГВМ и ГВК.
Аналоговое математической моделирование с применением аналоговой электронной и оптоэлектронной элементной базы на физическом уровне в настоящее время применяется сравнительно редко только в тех случаях, когда это дает выигрыш по сравнению с цифровой схемотехникой в 100…1000 раз по производительности, потребляемой мощности и габаритам. Это электронные и оптоэлектронные СБИС аналоговых нейрокомпьютеров, позволяющие строить узкоспециализированные ЭВМ, решающие некоторые сложные задачи за 10 мкс…1 мс. Это аналоговые процессоры нечеткого логического вывода, имитирующие в системах автоматики действия человека-оператора. Это однотактные оптические устройства преобразования Фурье плоских изображений, представляющие собой две системы линз, между которыми на пути световых лучей помещается полупрозрачный электрически управляемый транспарант обрабатываемого изображения. Результаты обработки снимаются матрицей фото-электрических преобразователей в задней фокальной плоскости. Машины такой организации относятся к специализированным и будут рассмотрены в следующей дополнительной учебной дисциплине.
2. Компьютерная обработка изображений
2.1 Определение компьютерной обработки изображений
Компьютерная обработка и распознавание изображений представляет собой быстро развивающуюся самостоятельную дисциплину. Компьютерная обработка изображений предполагает обработку цифровых изображений с помощью компьютеров или специализированных устройств, построенных на цифровых сигнальных процессорах. При этом под обработкой изображений понимается не только улучшение зрительного восприятия изображений, но и классификация объектов, выполняемая при анализе изображений.
В 60-е годы прошлого века получила развитие особая наука об изображениях – «иконика», которая посвящена исследованиям общих свойств изображений, целей и задач их преобразования, обработки и воспроизведения, распознавания графических образов [1].
Термин «иконика» происходит от греческого «eikon», что означает изображение, образ. Сегодня под ним понимают «создание и обработку изображений с помощью ЭВМ, что совпадает с понятием компьютерной обработки изображений.
Области применения цифровой обработки в настоящее время значительно расширяются, вытесняя аналоговые методы обработки сигналов изображений. Методы цифровой обработки широко применяются в промышленности, искусстве, медицине, космосе. Они применяются при управлении процессами, автоматизации обнаружения и сопровождения объектов, распознавании образов и во многих других приложениях.
Цифровая передача изображений с космических аппаратов, цифровые каналы передачи сигналов изображений требуют обеспечения передачи все больших потоков информации. Если при передаче цифрового сигнала цветного телевидения необходимо передавать потоки порядка 216 Мбит/с, то для передачи телевидения высокой четкости скорость передачи должна составлять порядка 1 Гбит/c. Формирование изображений, улучшение качества и автоматизация обработки медицинских изображений, включая изображения, создаваемые электронными микроскопами, рентгеновскими аппаратами, томографами и т.д., являются предметом исследования и разработки. Сегодня в медицинской технике широко применяются системы формирования изображения, его преобразования в цифровую форму, визуализация и документирование путем введения в компьютер изображений с помощью специализированных устройств захвата видео.
Автоматический анализ в системах дистанционного наблюдения широко применяется при анализе местности, в лесном хозяйстве, например, для автоматического подсчета площади вырубок, в сельском хозяйстве для наблюдения за созреванием урожая, при разведке, в системах противопожарной безопасности. Контроль качества производимой продукции выполняется благодаря автоматическим методам анализа сцен.
Компьютерная обработка изображений применяется в задачах экспертизы живописи неразрушающими методами [2]. Для восстановления старых фильмов применяются методы автоматической компенсации дефектов видеоматериала, полученного после преобразования киноизображения в видео.
Сегодня трудно представить область деятельности, в которой можно обойтись без компьютерной обработки изображений. Интернет, сотовый телефон, видеокамера, фотоаппарат, сканер, принтер, так прочно вошедшие в наш быт, – немыслимы без компьютерной обработки изображений.
При компьютерной обработке изображений решается широкий круг задач, таких как улучшение качества изображений; измерение параметров; спектральный анализ многомерных сигналов; распознавание изображений; сжатие изображений.
Устройства формирования изображений получили широкое распространение и применение в самых различных областях науки, техники, промышленности, медицине, биологии и др. [3–6]. Они являются неотъемлемыми компонентами систем и устройств, применяемых в фотокинотехнике, телевидении, системах технического зрения: дневного, ночного и теплового видения, при дистанционном зондировании Земли. Назначение этих систем предполагает решение комплекса технических и научных задач, требующих синтеза и анализа методов обработки, бинаризации, классификации изображений. Развитие микроэлектроники, переход от аналоговой формы сигналов к цифровой позволяют расширить палитру и повысить сложность применяемых алгоритмов для решения поставленных задач [7,8]. Рассмотрим некоторые из устройств формирования изображений.
2.2 Устройства формирования изображений
Устройства формирования изображений позволяют создавать изображения, порождаемые электромагнитным излучением в спектре от гамма излучения до инфракрасного (ИК). Рассмотрим некоторые из устройств формирования, которые включают электровакуумные и твердотельные фоточувствительные приборы.
Электровакуумные фоточувствительные приборы имеют фотокатод, эмитирующий электроны, и анод, на который подается положительный потенциал. Большинство передающих электровакуумных трубок и систем на их основе работают в видимом диапазоне. Отдельную группу оптико – электронных систем составляют приборы ночного видения, работающие в ближнем ИК диапазоне. Приемником и преобразователем ИК излучения в видимый диапазон в них является электронно – оптический преобразователь (ЭОП) [9]. В ЭОП анодом является люминисцентный экран, создающий видимое изображение при бомбардировке его электронами. Таким образом, он преобразует оптическое излучение в оптическое излучение, а не в электрический сигнал.
Передающие электроннолучевые трубки (телевизионные) преобразуют оптическое излучение в электрический сигнал. В электровакуумных фотоприборах возможна регистрация предельно малых оптических сигналов на уровне единичных фотоэлектронов, высокое разрешение. Основные недостатки – это сложные вакуумные стеклянные и металлоконструкции, ограниченный срок службы катодов, мишеней и анодов, высокие напряжения питания; ослепление, ограничение спектральной чувствительности близким ИК диапазоном, большие массогабаритные характеристики.
Твердотельные фоточувствительные приборы обеспечивают преобразование оптических сигналов в электрические в твердом теле. Существует два класса твердотельных фоточувствительных приборов: квантовые и тепловые приемники излучения.
Квантовые фотоприемники основаны на изменении электрических свойств полупроводника при поглощении фотона. Фотон передает свою энергию электрону, переводя его на более высокий энергетический уровень. Этот процесс фотогенерации сопровождается формированием пары носителей электрон и дырка. К таким приборам относятся фотодиоды, фоторезисторы, приборы с зарядовой связью (ПЗС). ПЗС обеспечивают высокое разрешение (размеры элементов растра менее 10 мкм), большие форматы (768x576 и больше), возможность управления экспонированием, высокую однородность чувствительности элементов, большее, чем в ЭЛТ, отношение сигнал/шум (С/Ш), малые габариты, вес и потребляемую мощность, имеют сравнительно низкую стоимость и большую номенклатуру изделий.
Тепловые твердотельные приемники излучения используют эффект изменения электрических свойств материала (емкости, сопротивления) при изменении его температуры вследствие нагрева при поглощении теплового излучения (при радиационном нагреве). Болометрическим эффектом называется изменение электрического сопротивления материала R при радиационном нагреве вследствие изменения температуры T этого материала. Болометрический эффект характеризуется температурным сопротивлением материала
![]() =,
=,
где R – сопротивление материала (чувствительного слоя болометра) при температуре T . Приемник, построенный на основе этого эффекта, называется болометром. К фотоприемным устройствам резисторного типа относятся микроболометрические матрицы. Термочувствительный слой элементов таких матриц изготавливается из пленок окислов ванадия, кремния и германия. Для устранения влияния температуры окружающей среды, приводящей к нестабильности параметров, микроболометр заключают в вакуумированный корпус с термоэлектрической системой стабилизации рабочей температуры. Оптический модулятор не нужен. Сегодня эти приемники уступают охлаждаемым фотонным матричным приемникам по чувствительности, размерам элементов и быстродействию [10].
Второй тип приборов – это пироэлектрические фотоприемники. Они используют тонкие пленки особых кристаллических диэлектриков, обладающих пироэлектрическим (ферроэлектрическим) эффектом. Чувствительный элемент в таких приемниках представляет собой ферроэлектрический конденсатор, при изменении температуры которого, изменяется его диэлектрическая постоянная, а, следовательно, и емкость.
Изменение емкости при постоянном приложенном к конденсатору напряжении, приводит к изменению заряда, поступающего от конденсатора на схему считывания сигнала. Поскольку изменение заряда происходит только при изменении температуры, то для наблюдения за объектами с постоянной температурой, необходимо модулировать падающее излучение. Осуществляется это обтюратором, который с частотой кадров перекрывает падающий на приемник поток излучения. В качестве диэлектриков используются ниобат калия тантала (KTN ), титанат барий-стронций (BST ) и другие виды керамики. Достоинствами пироэлектрических приемников являются почти равномерная спектральная чувствительность в широком диапазоне (от 800 нм до 25 мкм), высокая временная стабильность и низкая стоимость.
Третий тип тепловых приборов построен на использовании термопар (термоэлектрические матрицы). Два слоя разнотипных металлов/ полупроводников образуют термопару. Один слой облучается радиацией и нагревается, второй – экранирован от обучения. Между ними возникает термо ЭДС U
. Величина ЭДС пропорциональна производной от этой ЭДС по температуре ![]() = ∂U /
∂T.
Термопара является генератором напряжения. При последовательном включении термоэлементов чувствительность возрастает пропорционально числу включенных элементов. Стабилизатор температуры не нужен. Термопары часто образуют пленками алюминия и поликристаллического кремния, расположенными друг под другом. Пленки разделены слоем
= ∂U /
∂T.
Термопара является генератором напряжения. При последовательном включении термоэлементов чувствительность возрастает пропорционально числу включенных элементов. Стабилизатор температуры не нужен. Термопары часто образуют пленками алюминия и поликристаллического кремния, расположенными друг под другом. Пленки разделены слоем ![]() [11]. Термоэлементы имеют линейные рабочие хаарктеристики, не требуют обтюрации (в отличие от пироэлектрических приемников), работают без термостабилизации, не требуют источников питания.
[11]. Термоэлементы имеют линейные рабочие хаарктеристики, не требуют обтюрации (в отличие от пироэлектрических приемников), работают без термостабилизации, не требуют источников питания.
Независимо от типа матричного фотоприемника общей тенденцией остается увеличение формата. При этом снижение размеров чувствительных элементов подошло к теоретическому пределу. Совершенствование технологии производства приемников направлено, прежде всего, на уменьшение темнового тока с целью повышения пороговой чувствительности, повышение однородности чувствительности элементов, повышение чувствительности элементов, уменьшение перекрестных межэлементных помех.
Неохлаждаемые приемники ИК излучения все еще отстают от традиционных охлаждаемых по температурному разрешению. Однако их основные параметры (чувствительность, пространственное и температурное разрешение) в последние годы улучшаются, что в сочетании с такими преимуществами, как отсутствие холодильника, низкая стоимость, формат кадра порядка 640x480 элементов, обусловливают все более широкое их применение в мобильных тепловизионных системах широкого применения.
2. Математические модели изображений
2.1 Модели непрерывных изображений
Компьютерная обработка изображений возможна после преобразования сигнала изображения из непрерывной формы в цифровую форму. Эффективность обработки зависит от адекватности модели, описывающей изображение, необходимой для разработки алгоритмов обработки. При этом необходимо учитывать влияние передающей и приемной систем и канала связи на сигнал изображения. Модель изображения представляет систему функций, описывающих существенные характеристики изображения: функцию яркости, отражающую изменение яркости в плоскости изображения, пространственные спектры и спектральные интенсивности изображений, функции автокорреляции. Канал изображения содержит оптическую систему, оптико – электрический преобразователь, устройство аналого – цифрового преобразования (АЦП) и цифровой обработки сигналов изображения. В общем случае непрерывное изображение может быть представлено функцией пяти аргументов: трех пространственных координат, времени и длины волны электромагнитного излучения. Упрощения модели пространственно – временных сигналов в некотором диапазоне волн f (x, y, z, t, λ) приводят к моделям пространственно – временного сигнала f (x, y, z, t ), пространственного сигнала f (x, y, z ), временного сигнала f (t ). Здесь x, y, z – пространственные координаты, t – время, λ – длина волны электромагнитного излучения.
2.2 Пространственные спектры изображений
Спектр изображения получают прямым двумерным преобразованием Фурье функции, описывающей изображение [12]:
F
(![]() ,
,
![]() )
)![]() =
=![]() f
(x, y
) exp (−i
(ωx
x
+ ω y
y
)) dxdy
, (2.1)
f
(x, y
) exp (−i
(ωx
x
+ ω y
y
)) dxdy
, (2.1)
где ωx,
ωy
– пространственные частоты; i
= ![]() , мнимая единица.
, мнимая единица.
Функция exp (−i (ωx x + ωy y )) при фиксированных значениях пространственных частот описывает плоскую волну в плоскости изображения (x, y ). Формула (2.1) связывает вещественную функцию, описывающую яркость изображения f (x , y ) с комплексной функцией частоты – спектром изображения F (ωx, ωy) :
F
(![]() ,
,
![]() )
)
![]() =
=![]() f
(x, y
) cos (−i
(
f
(x, y
) cos (−i
(![]() ,
,
![]() )) dxdy+
)) dxdy+
+i
![]() (− f
(x, y
) sin (
(− f
(x, y
) sin (![]() ,
,
![]() )) dxdy=Re(
)) dxdy=Re(
![]() ,
,
![]() )+i Im(
)+i Im(
![]() ,
,
![]() )
, (2.2)
)
, (2.2)
где Re (ωx , ωy ) – реальная часть спектра; Im (ωx , ωy ) – мнимая часть спектра.
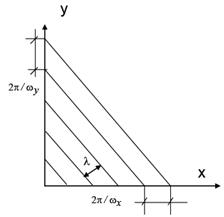
Рисунок 2.1 Определение пространственных частот изображения.
Амплитуда и фаза спектра определяются по формулам (2.3) и (2.4) соответственно:
F
(![]() ,
,
![]() )
=
)
= ![]()
![]()
ϕ (щx
,
щy
)
= arctg (Im
(![]() ,
,
![]() )
/
Re
(
)
/
Re
(![]() ,
,
![]() )).
)).
Из (2.3)
(ω ω) = x
y
F
,
F(![]() ,
,
![]() ) exp (i
ϕ(
) exp (i
ϕ(![]() ,
,
![]() )
). (2.4)
)
). (2.4)
Обратное преобразование Фурье позволяет восстановить изображение по его спектру:
f
(x
,
y
) = (1/
4![]() )
)![]()
![]() F
(
F
(
![]() ,
,
![]() )
exp (i
(
)
exp (i
(![]() ,
,
![]() ))
))![]() (2.5)
(2.5)
2.3 Спектральные интенсивности изображений
Спектральная интенсивность изображения характеризует
распределение энергии по пространственным частотам. Она определяется как квадрат модуля спектра изображения:
S(![]() ,
,
![]() ) = Re
) = Re
![]() + Im
(
+ Im
(![]() ,
,
![]() =
=![]() ((
((![]() ,
,
![]() )). (2.6)
)). (2.6)
Для ее названия используются термины спектральная плотность и энергетический спектр.
Энергия изображения определяется как интеграл энергетического спектра по пространственным частотам. В соответствии с теоремой Парсеваля энергия изображения может быть вычислена в соответствии с (2.7):
![]()
![]() (
x
,
y
)
dxdy
=
(
x
,
y
)
dxdy
=
![]()
![]()
![]()
2.4 Вероятностные модели изображений и функции Автокорреляции
Вероятностные модели изображений широко используются для описания изображений. Изображение в этом случае рассматривается как случайная функция пространственных координат (x, y ) и времени t . Случайный процесс называется стационарным в широком смысле , если он имеет постоянные значения математического ожидания и дисперсии, а его автокорреляционная функция зависит не от координат, а от их разностей (сдвига). Случайный процесс называется стационарным в узком смысле , если его n ‑мерная плотность распределения вероятностей инвариантна к сдвигу. В этом случае не зависят от времени и моменты более высокого порядка, в частности, асимметрия и эксцесс. Случайный процесс описывается плотностью вероятности распределения яркости в изображении по пространственным координатам для некоторого фиксированного момента времени t p (x , y ).
В соответствии с определением математическое ожидание (среднее значение) стационарного процесса в широком смысле
Mf
= ![]() f (x, y) p
(x, y
) dxdy
=const. (2.8)
f (x, y) p
(x, y
) dxdy
=const. (2.8)
Дисперсия
Df
=σ 2=E
(f
(x, y
) – ξ ![]() =
= ![]() (f (x, y) –
ξ
(f (x, y) –
ξ![]() p
(x, y
) dxdy
=const. (2.9)
p
(x, y
) dxdy
=const. (2.9)
Функция автокорреляции вычисляется в соответствии с (2.10):
R
(
![]() ,
,
![]() )
= =
)
= = ![]() f
(
x
,
y
)
f
(
f
(
x
,
y
)
f
(
![]() ,
,
![]() ))
dxdy
,
(2.10)
))
dxdy
,
(2.10)
где ![]() ,
,
![]() задают сдвиги изображения по соответствующим осям координат.
задают сдвиги изображения по соответствующим осям координат.
Для действительной функции f автокорреляционная функция является действительной и четной. Спектр двумерной автокорреляционной функции изображения (прямое преобразование Фурье автокорреляционной функции) равен энергетическому спектру изображения (спектральной плотности мощности) по определению:
S
(
![]() ,
,
![]() )
=
)
=![]() R
(
R
(
![]() ,
,
![]() )
exp (− i
(
)
exp (− i
(
![]() +
+ ![]() d
d
![]() d
d
![]() . (2.11)
. (2.11)
Стационарный случайный процесс называется эргодическим , если любая его вероятностная характеристика может быть получена из одной реализации путем усреднения по времени. При этом среднее по времени равно среднему по ансамблю реализаций. Свойство эргодичности используется при оценке вероятностных характеристик изображений.
2.5 Критерии качества изображений
Качество изображения может определяться статистическими, спектральными, яркостными характеристиками изображения. В большинстве практических применений качество рассматривается как мера близости двух изображений: реального и идеального или преобразованного и исходного. При таком подходе можно оценивать как субъективную степень похожести изображений, так и получать объективные оценки параметров сигналов изображения: моменты первого и второго порядка разностного сигнала сравниваемых изображений, такие параметры преобразования как отношение С/Ш, коэффициенты сжатия информации и другие.
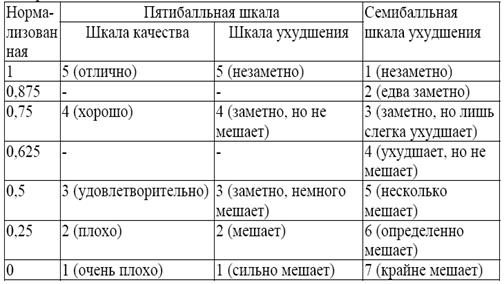
Субъективные критерии – это критерии визуального восприятия, оцениваемые в процессе экспертизы некоторой группой наблюдателей (экспертов). Наибольшее распространение получил метод оценок, при котором наблюдатель оценивает качество изображения в баллах по определенной шкале, считая, что идеальное изображение имеет максимальный балл. Этот метод позволяет оценить такие характеристики изображения как правильность цветопередачи, координатные искажения, чистоту переходов и др. Основные шкалы оценок при использовании метода сравнения приведены в таблице 2.1 [13].
Для интерпретации полученных экспертных оценок разработаны методы их представления, например построение кумулятивных кривых распределения оценок как функции от искажений. Средняя оценка определяется по формуле
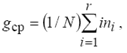
где N ‑общее число оценок, ni – число оценок равных i баллам, r – количество видов разных оценок.
Нормализованные оценки p выражают относительное качество в диапазоне [0,1]. При пятибалльной системе, когда g ∈ [1,5]:
p = (g −1) / 4,
а средняя оценка вычисляется в соответствии с формулой:
p
ср = (![]() + 0,75
+ 0,75![]() + 0,5
+ 0,5![]() + 0,25
+ 0,25![]() )/ N.
)/ N.
Таблица 2.1 Основные шкалы субъективных оценок качества изображения
Единицей ухудшения качества телевизионных (ТВ) изображений является имп (от impairment – ухудшение, повреждение). Эта единица введена Проссером, Аллнаттом и Льюисом в 1964 г. и используется МККР (Международным консультативным комитетом по радиосвязи (CCIR )). Ухудшение обратно пропорционально нормализованной оценке качества и
изменяется от ∞ до 0 при изменении p от 0 до 1 в соответствии с формулой:
I =1 / p −1.
Достоинство методики оценки ухудшения состоит в том, что результирующая оценка ухудшения получается арифметическим суммированием оценок ухудшения, вызванных различными видами искажений сигналов изображения. Основываясь на психофизических свойствах наблюдателя, субъективные оценки позволяют характеризовать восприятие изображения. Интегральный критерий качества формируется по обобщенной формуле:
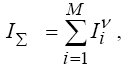
где M ‑ число параметров, по которым оценивается качество изображения; ν – показатель степени. Значение показателя степени принимают равным 1, но могут быть использованы, например, такие значения как 0,78 или 2. В настоящее время применяются и другие оценки качества изображений. При
разработке аппаратных средств специального назначения большое значение имеет оценка объективных характеристик качества преобразованного изображения. Объективными критериями, используемыми при оценке качества изображений, являются критерии, позволяющие получить просто вычисляемую характеристику изображения разностного сигнала. К таким критериям относится, прежде всего, среднеквадратический критерий. По нему мерой различия двух изображений f
(x
, y
) и ![]() (x, y
) является среднеквадратическое значение разностного сигнала двух изображений. Для непрерывных изображений, заданных при x
∈[0, N
] и y
∈[0, M
], среднеквадратическое отклонение (СКО) вычисляется по формуле:
(x, y
) является среднеквадратическое значение разностного сигнала двух изображений. Для непрерывных изображений, заданных при x
∈[0, N
] и y
∈[0, M
], среднеквадратическое отклонение (СКО) вычисляется по формуле:
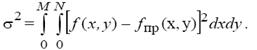 (2.12)
(2.12)
В некоторых случаях используется критерий максимальной ошибки, который в отличие от (2.12), позволяет установить значение максимальной ошибки преобразования:
![]() = max |f
(x
,
y
) –
= max |f
(x
,
y
) – ![]() | (2.13)
| (2.13)
(x , y )
Применяются и другие объективные критерии качества изображений [14]. Существует определенное разногласие в оценках качества, даваемых человеческим глазом (субъективных), и объективных, полученных в виде количественных показателей. Глаз является совершенным изобретением природы, с ним не могут соревноваться достаточно примитивные объективные оценки типа СКО, пикового отношения сигнал/шум (ПСШ) и др. Поэтому некоторые результаты, рассматриваемые с точки зрения объективных оценок как одинаковые, визуально могут восприниматься различно. Однако объективные критерии используются при компьютерной обработке изображений в системах с автоматическим принятием решений. Функционирование автоматических компьютерных систем полностью подчинено математическим критериям, и качество их работы оценивается только объективными показателями. Понятно, что и качество изображений, используемых в этих системах, также должно оцениваться только по объективным критериям.
Заключение
Нейронные сети основывались на высокоуровневом моделировании процесса мышления на обычных компьютерах. Чтобы создать искусственный интеллект, необходимо построить систему с похожей на естественную архитектурой, т.е. перейти от программной реализации процесса мышления к аппаратной.
Основу нейросетей составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга – искусственные нейроны.
Естественным продолжением аппаратного и программного подхода к реализации нейрокомпьютера является программно-аппаратный подход. Аппаратный подход связан с созданием нейрокомпьютеров в виде нейроподобных структур (нейросетей) электронно-аналогового, оптоэлектронного и оптического типов. Для таких компьютеров разрабатываются специальные СБИС (нейрочипы, нейроускорители).
Список используемой литературы
1. А. Горбань, Д. Россиев. Нейронные сети на персональном компьютере. // Новосибирск: Наука, 1996.
2. Ф. Уоссермен, Нейрокомпьютерная техника, М., Мир, 1992.
3. Итоги науки и техники: физические и математические модели нейронных сетей, том 1, М., изд. ВИНИТИ, 1990.
4. http://therocker.narod.ru/doc/neuro.htm#comp1
5. Marguerat C. Artificial neural network algorithms on a parallel DSP system. In: Transputers’94 Advanced research and industrial applications. Proc. Of the International conf. 21–23 Sept. 1994. IOS Press 1994, p. 278–287.
6. MD 1220 Data Sheet. March 1990, Micro Devices, 30 Skyline Dr., Lake Mary, F1 32746–6201, USA.
7. NXL420 Data Sheet. June 1992, Neurologix, Inc., 800 Charcot Av., Suite 112, San Jose. Ca. USA.
8. M. Yasunga, N. Msuda, M. Yagyu, M. Asai, M. Yamada, A. Masaki, Design, Fabrication and Evaluation of a 5‑Inch Wafer Scale Neural Networks LSI Composed of 576 Digital Neurons, Proc. Int. Joint Conf. on Neural Networks IJCNN» 90, June 1990.
9. 80170NX Electrically Trainable Analog Neural Network, Data Sheet, Intel Corp., Santa Clara, CA, 1991.
10. J. Alspector, T. Jayakumar, S. Luna. Experimental Evaluation of Learning in a Neural Microsystem, Proc. Of NIPS» 91 in Advances in Neural Information Processing Systems‑4, pp. 871–878, Morgan-Kaufmann Pub., San Mateo, CA, 1992.
11. Виксне П., Черников В., Фомин Д., Шевченко П. Применение микропроцессора NM6403 для эмуляции нейронных сетей. Сборник докладов V Всероссийской конференции «Нейрокомпьютеры и их применение». Москва, 17–19 февраля 1999.
12. Терехов В.А., Ефимов Д.В., Тюкин И.Ю. Нейросетевые системы управления. – 1-е. – Высшая школа, 2002. – С. 184. – ISBN 5–06–004094–1
13. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – 1-е. – М.: Горячая линия – Телеком, 2001. – С. 382. – ISBN 5–93517–031–0
14. Каллан Р. Основные концепции нейронных сетей = The Essence of Neural Networks First Edition. – 1-е. – «Вильямс», 2001. – С. 288. – ISBN 5–8459–0210‑X
15. Ясницкий Л.Н. Введение в искусственный интеллект. – 1-е. – Издательский центр «Академия», 2005. – С. 176. – ISBN 5–7695–1958–4
16. Комарцова Л.Г., Максимов А.В. Нейрокомпьютеры. – 1-е. – Изд-во МГТУ им. Н.Э. Баумана, 2002. – С. 320. – ISBN 5–7038–1908–3