| Похожие рефераты | Скачать .docx |
Курсовая работа: Решение математических задач с помощью алгоритмического языка Turbo Pascal, Microsoft Excel, пакета MathCAD и разработка программ в среде Delphi
Московский Гуманитарный Техникум Экономики и Права
Курсовая работа по курсу:
Информатика, вычислительная
техника и программирование на ПЭВМ
Решение математических задач с помощью алгоритмического языка Turbo Pascal, Microsoft Excel, пакета MathCAD и разработка программ в среде Delphi"
Москва 2008
Содержание
Задание1 (а) Решение циклических программ
Задание 1 (б) Решение программы вычисления функции с условием
Решение уравнения в табличном редакторе Microsoft Excel
Задание 1 (в) вычисление массива
Решение уравнения в Turbo Pascal
Задание 1 (г) вычисление суммы в Microsoft Excel
Задание 2. Интегрирование функции
Вычислить определённый интеграл
1. Метод прямоугольников
2. Метод трапеции
3. Метод симпсона
4. С автоматическим выбором шага
Задание 3. Решение системы линейных уравнений
Решение уравнения с помощью MathCAD
Задание 4. Решение нелинейного уравнения
Задание 5. Организация нахождения минимума и максимума элемента в массиве случайных чисел в среде пакета MathCAD
Задание 6
Задание 1. Решение уравнения в табличном редакторе Microsoft Excel
Табличный редактор Microsoft Excel представляет собой электронную таблицу разбитую на ячейки.
В ячейки одного из столбцов вводятся значения переменной В ячейки другого столбца, строка которого соответствует номеру первой ячейки столбца переменных, ставят "=" и вводят формулу. Затем нажимают Enter и табличный редактор выполняет поставленную задачу.
Решение уравнения с помощью MathCAD.
Данная задача в MathCAD будет выполнятся с использованием ранжированной переменной. В среде пакета MathCAD для выполнения итеративных вычислений предусмотрен аппарат ранжированных переменных.
Ранжированная переменная-это переменная, которой приписан диапазон изменения значений.
Пример ранжированной переменной:
x: =a,b. c,
где x - переменная, a,b,c - значения, которые принимает переменная, т.е. a-первое значение, b-второе значение, т.е. (b-a) - шаг изменения переменной, и c-последнее значение.
Функция представлена в виде ранжированного выражения, т.е. выражения в котором присутствуют p-переменные.
Решение уравнения в Turbo Pascal
Арифметические выражения строятся из констант, переменных, функций и операций над ними.
Правила использования выражений:
1. Выражение записывается в одну строку.
2. Используются только круглые скобки, число открывающихся скобок должно соответствовать числу закрывающихся скобок.
3. Нельзя записывать подряд два знака арифметических операций.
Структура программы в Turbo Paskal
Program <имя программы> ; ] 1
![]() uses
<описание модулей>;
uses
<описание модулей>;
lable <метки>;
const <объявление констант>;
type <объявление типов данных>; 2
var < объявление переменных>;
![]() < описание процедур и функций>;
< описание процедур и функций>;
begin
операторы 3
end .
Заголовок программы: служебное слово program и имя;
Раздел описаний: описываются все идентификаторы объектов, используемые в данной программе. Описать идентификатор - значит указать его имя и тип.
Раздел операторов: указывается последовательность действий, которые необходимо.
Повторение (циклический алгоритм) - это алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий.
Последовательность действий, выполняемая в цикле, называется телом цикла.
Переменная, которая хранит число повторений цикла, называется параметром (счетчиком) цикла.
Цикл позволяет многократно выполнять отдельный оператор или последовательность операторов.
Различают следующие циклы: с параметром, с предусловием, с пост условием.
Цикл с предусловием и пост условием, как правило, используется для организации приближенных вычислений, задач поиска и обработки данных, вводимых с клавиатуры или файла.
| С предусловием |
С постусловием |
| WHILE условие DO BEGIN Оператор1 Оператор2 END: |
REPEAT Оператор1 Оператор2 UNTIE условие |
| Может не выполниться ни разу |
Выполнится хотя бы один раз |
| Параметр цикла проверяется до тела |
Параметр цикла проверяется после тела |
| Записывается условие выполнения цикла |
Записывается условие выхода из цикла |
Цикл с параметром используется, если известно число повторений и реализуется с помощью оператора FOR общий вид которого следующий:
FOR параметр цикла: = начальное значение TO (DOWNTO) конечное значение
DO BEGIN Оператор1
Оператор2
END:
Параметр должен быть переменной целого типа.
Если используется слово TO, счетчик увеличивается на единицу, если используется слово BOWNTO, то счетчик уменьшается на единицу.
Задание1 (а) Решение циклических программ
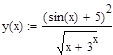
Xn=2; Xk=10; h=1.
В Microsoft Excel:
Во втором столбце формула имеет выд: = (SIN (A2) +5) ^2/СТЕПЕНЬ (A2+3^ (A2); 1/2);
| Значение x: |
y (x): |
|
| 2 |
10,53 |
|
| 3 |
4,826 |
|
| 4 |
1,953 |
|
| 5 |
1,037 |
|
| 6 |
0,822 |
|
| 7 |
0,683 |
|
| 8 |
0,443 |
|
| 9 |
0, 209 |
|
| 10 |
0,082 |
|
В Mathcad:
![]()
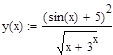


В Turbo Paskal:
program z1;
uses crt;
var Xn,Xk,X,Y,H,Z: REAL;
begin
clrscr;
write ('Vvedite Xn,Xk,H=');
readln (Xn,Xk,H);
X: =Xn;
repeat
z: =x+exp (x*ln (3));
if z<=0 then writeln ('NO') else
Y: =sqr (sin (x) +5) /Sqrt (z);
writeln ('X=',X: 6: 1,' Y=',Y: 8: 3);
X: =X+H;
until X>=Xk+H/2;
readkey;
end.
Блок-схема к заданию:
 |
Результаты вычислений:

Задание 1 (б) Решение программы вычисления функции с условием
Решение уравнения в табличном редакторе Microsoft Excel
Для реализации задачи необходимо использовать логическую функцию ЕСЛИ, которая возвращает одно значение, если заданное условие при вычислении дает значение ИСТИНА Реализация задачи вычисления функции с условиями , и другое значение, если ЛОЖЬ. Общий вид функции такой:
ЕСЛИ (лог_выражение; значение_если_ложь)
Лог выражения -это любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.
Значение_если_истина -это значение, которое возвращается, если лог_выражение имеет значение ИСТИНА. Если лог_значение имеет значение ИСТИНА и значение_если_истина опущено, то возвращается значение ИСТИНА. Значение_если_истина может быть другой формулой.
Значение_если_ложь- это значение, которое возвращается, если лог_выражение имеет значение ЛОЖЬ. Если лог_выражение имеет значение ЛОЖЬ и значение_если_ложь опущено, то возвращается значение ЛОЖЬ. Значение_если_ложь может быть другой формулой.
В Microsoft Excel:
Во втором столбце формула имеет вид: =ЕСЛИ (A2=0; "NO"; ЕСЛИ (A2<0; SIN (A2) / (1-2^SIN (A2)); ЕСЛИ (И (A2>0; A2<1); 2*A2/ (1-A2); ЕСЛИ (A2>1; A2^2-LN (A2); "нет решения"))))
Рисунок.
x |
y (x) |
|||||||
| -2 |
-1,9447896 |
|
||||||
| -1,6 |
-1,9997383 |
|||||||
| -1,2 |
-1,9585469 |
|||||||
| -0,8 |
-1,8309758 |
|||||||
| -0,4 |
-1,646153 |
|||||||
| 0 |
NO |
|||||||
| 0,4 |
1,33333333 |
|||||||
| 0,8 |
8 |
|||||||
| 1,2 |
1,25767844 |
|||||||
| 1,6 |
2,08999637 |
|||||||
| 2 |
3,30685282 |
|||||||
В Mathcad:
![]()



В Turbo Pascal:
program z2;
uses crt;
label 20;
var x,y,Xn,Xk,h: real;
begin clrscr;
writeln ('Please ENTER Xn,Xk,h=');
readln (Xn,Xk,h);
x: =Xn;
while x<=Xk+h/2 do
begin
if x<0 then
begin
y: =1-exp (sin (x) *ln (2));
if y=0 then
writeln ('NET KORNEY') else
y: =sin (x) /y;
end
else
if (x>0) and (x<1) then y: = (2*x) / (1-x) else
if x>1 then y: =x*x-ln (x)
else
begin
writeln ('NO answer');
goto 20;
end;
writeln ('x=',x: 3: 1,' y=',y: 6: 3);
20: x: =x+h;
end;
readkey;
end.
Результаты вычислений:

Блок-схе

ма к заданию:
Задание 1 (в) вычисление массива
Решение уравнения в Turbo Pascal
Массив (матрица, таблица, вектор) - это структура данных, представляющая собой совокупность элементов одного типа.
Массив называется одномерным, если для получения доступа к его элементам достаточно одной индексной переменной.
1) Массив можно определить как одномерную (последовательную) совокупность элементов некоторого типа, которые адресуется с помощью индекса.
2) Массив должен быть объявлен в разделе описания переменных:
VAR ИмяМассива: ARRAY ( НачИндекс. КонечныйИндекс) OF ТипДанных.
3) Доступ к элементу массива осуществляется путем указания индекса (номера), в качестве которого нужно использовать переменную целого типа. Massiv (2): =5;
А: =massiv (4);
4) Для ввода, вывода и обработки массивов удобно использовать операторы циклов. Задание элементов массива случайным образом.
Необходимо массив yi из случайных чисел, входящих в определенный интервал. Для этого нужно использовать функцию Random (x), которая возвращает случайное число от 0 до X, если функция используется без параметра, то будут генерировать числа от 0 до 1.
Перед использованием данной функции необходимо применить оператор Randomize, который обеспечивает несовпадение последовательности случайных чисел, генерируемых функцией.
В Microsoft Excel:
Во втором столбце формула имеет вид: =СТЕПЕНЬ (EXP (1) ^ (3*A2) - TAN (A2) ^3; 1/5) /КОРЕНЬ ( (A2) ^2+SIN (A2) ^2)
Рисунок.
| x |
y |
|
| 0,4 |
2,267 |
|
| 0,7 |
1,576 |
|
| 0,8 |
1,473 |
|
| 1,3 |
0,752 |
|

В Mathcad:
![]()



В Turbo Pascal:
program zadanie3;
uses crt;
const n=4;
var x,y: array [1. n] of real;
i: integer;
z,j,d: real;
begin
clrscr;
for i: =1 to n do
begin
write ('Enter x [i] =');
readln (x [i]);
end;
for i: =1 to n do
begin
j: =exp (3*x [i]) - exp (3*ln (sin (x [i]) /cos (x [i])));
z: =exp (1/5*ln (abs (j))) * (abs (j) /j);
d: =sqrt (sqr (x [i]) +sqr (sin (x [i])));
y [i]: =z/d;
writeln ('x [i] =',x [i]: 5: 1,' y [i] =',y [i]: 5: 3);
end;
readkey;
end.
Блок-схема алгоритма решения задания №1.3
 |
Нахождение функции заданном массиве:
Результаты вычислений:

Задание 1 (г) вычисление суммы в Microsoft Excel
В третьем столбце формула имеет вид: = (A2^ (-A2*SIN (A2)) - LN (2*A2+5)) / (КОРЕНЬ (2+SIN (2*A2)) +A2^2)
В четвертом столбце формула имеет вид: =СУММ (C2*B2+C3*B3+C4*B4+C5*B5)
| x |
a |
y |
S |
| 1,1 |
0,42 |
-0,368 |
-1,3 |
| 1,3 |
0,7 |
-0,399 |
|
| 1,5 |
0,9 |
-0,413 |
|
| 1,7 |
1,2 |
-0,408 |
В Mathcad:
![]()
![]()
![]()





В Turbo Pascal:
Program Summa;
uses crt;
const n=4;
Var x,z,d,Xn,h,F,S: Real;
i: Integer;
a: array [1. n] of Real;
BEGIN
clrscr;
randomize;
Write ('enter please Xn,h=');
ReadLN (Xn,h);
for i: =1 to n Do
begin
Write ('enter please a [i] =');
ReadLN (a [i]);
end;
x: =Xn;
S: =0;
for i: =1 to n Do
begin
z: =exp ( (-x*sin (x)) *ln (x)) - ln (2*x+5);
d: =sqrt (2+sin (2*x)) +sqr (x);
F: =z/d;
S: =S+F*a [i] ;
x: =x+h;
end;
WriteLN ('S=',S: 10: 3);
readkey
END.
Результаты вычислений:

Блок-схема алгоритма решения задания №1.4
Нахождение функции, если дан x, h, n, задан массив :
 |
Задание 2. Интегрирование функции
Вычислить определённый интеграл

Так как определённый интеграл является площадью фигуры, ограниченной некоторой функцией y=f (x), то целью задачи является нахождение площади этой фигуры. Для этого необходимо данную фигуру разбить на более простые, площадь которых находится по простым формулам, а затем сложить полученные площади в одну для нахождения необходимой, т.е. для вычисления данного определённого интеграла.
Существуют различные методы нахождения определённого интеграла.
Рассмотрим некоторые из них:
метод средних прямоугольников;
метод трапеций;
метод Симпсона (парабол);
с автоматическим выбором шага;
1. Метод прямоугольников
Для вычисления приближённого значения определённого интеграла отрезок [a, b] делят на n равных частей точками
a=x0
<x1
<x2
<…<xn
=b![]()
так, что xi+1 -xi = (b-a) /n (I=0,1,2,…,n-1). Тогда длина каждого частичного отрезка определяется как h= (b-a) /n, а точки разбиения x0 =a, x1 =x0 +h, x2 =x1 +h,…, xn =xn -1 +h. Эти точки называются узлами, а h-шагом интегрирования. В узлах вычисляются ординаты y0 , y1 ,…, yn , т.е. yi =f (xi ). На частичных отрезках [xi ; xi +1 ] строятся прямоугольники, высота которых равна значению f (x) в какой-либо точке каждого частичного отрезка. Произведение f (xi ) *h определяет площадь частичного прямоугольника, а сумма таких произведений - площадь ступенчатой фигуры, представляющей собой приближённое значение интеграла.
Если f (xi
) вычисляется в левых концах отрезков [xi
; xi
+1
], то получается формула левых прямоугольников: ![]()
 »Iл
=
»Iл
=![]() (y0
+y1+…+
yn
-1
) =
(y0
+y1+…+
yn
-1
) = ![]()
 .
.
Если f (xi ) вычисляется в правых концах отрезков [xi ; xi +1 ], то получится формула правых прямоугольников:
 »Iп
=
»Iп
=![]() (y1
+y2+…+
yn
) =
(y1
+y2+…+
yn
) = ![]()
 .
.
Если функция f вычисляется в точках xi +h/2Î [xi ;; xi +1 ], то получается формула средних прямоугольников:

2. Метод трапеции
Метод трапеций аналогичен методу прямоугольников, с той лишь разницей, что на каждом частичном отрезке строится трапеция.
Приближенное значение интеграла равно сумме всех площадей частичных трапеций:
 »I=
»I=![]()
![]()
![]()
3. Метод симпсона
Если на частичном отрезке длиной 2h функции заменяется дугой параболы, то можно получить формулу парабол или обобщенную формулу Симпсона:
 = (h/3) * (y0
+y2
n
+
= (h/3) * (y0
+y2
n
+ ,
,
где
1 при i - нечетном;
Ci =
1 при i - чётном ;
4. С автоматическим выбором шага
Точность вычисления определенного интеграла зависит от величины шага интегрирования. Ошибка в выборе величины шага интегрирования либо не обеспечит нужной точности, либо приведет к необоснованным затратам машинного времени.
Заданную точность при рациональных затратах времени на вычисления обеспечивают алгоритмы интегрирования с автоматическим выбором шага. Идея метода автоматического выбора шага интегрирования для достижения заданной точности заключается в следующем:
а) выбирается начальное n и вычисляется шаг h= ( b- a) / n ;
б) рассчитывается значение интеграла I1 для этого шага h ;
в) шаг h уменьшается в два раза, т.е. h= h/2 и вычисляется значение интеграла I2 ;
г) оценивается погрешность между двумя значениями r= ½ I1 - I2 ½ ; если погрешность r меньше или равна заданной точности, т.е. r<= e , то точность достигнута и значение интеграла I= I2 ; если r> e , то точность не достигнута и величине I1 присваивается более точное значение I2 ;
д) теперь повторяются этапы в) и г) до выполнения условия r<= e .
Вычисление определенного интеграла с помощью пакета MathCAD в нормальном и символьном виде.
Для решения интеграла численно и в символьном виде необходимо задать функцию f (x) и найти от неё интеграл  на промежутке [a, b].
на промежутке [a, b].
Для вычисления численного значения заданного интеграла:
С помощью встроенных функций задаём определённый интеграл;
После нажатия клавиши "=", MathCAD выдаёт значение интеграла на заданном промежутке.
В Mathcad:
![]()

При решении интеграла в символьном виде:
С помощью встроенных функций задаём интеграл;
Вызов в меню "Математика" подменю "Булен" и нажатие "®" или Control+. приводит к вычислению интеграла в символьном виде.
В Mathcad:
![]()

В Turbo Pascal:
Текст программы вычисления
определенного интеграла методом
средних прямоугольников на TP
program Sredniipriamougolniki;
uses crt;
var a,b,h,s,y,x: real;
i,n: integer;
begin clrscr;
write ('Vvedite a,b,n=');
readln (a,b,n);
h: = (b-a) /n;
x: =a+h/2;
s: =0;
for i: =1 to n do
begin
s: =s+1/sqr (3*sin (x) +2*cos (x));
x: =x+h;
end;
y: =h*s;
writeln ('n=',n,' y=',y: 10: 3);
readkey;
end.
Результаты работы программы:
a=0 b=1 n=1000 y=0.117
Блок-схема алгоритма решения задания №2.1
Вычисление определенного интеграла методом средних прямоугольников :
 |
Текст программы вычисления
определенного интеграла методом
трапеции
program integral 2;
uses crt;
var a,b,h,S,S1,x,y: real;
i,n: integer;
function f (c: real): real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin clrscr;
write ('a,b,n=');
readln (a,b,n);
h: = (b-a) /n;
x: =a;
s: =0;
for i: =1 to n-1 do
begin
x: =x+h;
s: =s+f (x);
end;
S1: = f (a) +f (b);
y: = (h/2) * (S1+2*s);
writeln ('n=',n, ' y=',y: 8: 3);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 y=0.117
Блок-схема алгоритма решения задания № 2.2
 |
Вычисление определенного интеграла методом трапеции :
Текст программы вычисления
определенного интеграла
методом Симпсона
program simpson;
uses crt;
var a,b,h,x,y,s,s1: real;
i,n,c,m: integer;
function f (x: real): real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin clrscr;
write ('a,b,n=');
readln (a,b,n);
h: = (b-a) / (2*n);
x: =a;
s: =0;
c: =1;
m: =2*n-1;
for i: =1 to m do
begin
x: =x+h;
s: =s+ (3+c) *f (x);
c: =-c;
end;
s1: =f (a) +f (b);
y: = (h/3) * (s1+s);
writeln ('y=',y: 10: 3,' n=',n);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 y=0.117
Блок-схема алгоритма решения задания №2.3
 |
Вычисление определенного интеграла методом Симпсона :
![]() Текст программы вычисления
Текст программы вычисления
определенного интеграла с
автоматическим выбором шага
program avtomaticheskiyshag;
uses crt;
var e,a,b,s,h,sn,sn1: real;
i,n: integer;
function f (x: real): real;
var y: real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin
clrscr;
write ('a='); read (a);
write ('b='); read (b);
write ('e='); read (e);
sn: =0;
sn1: =0;
n: =100;
repeat
n: =n*2;
h: = (b-a) /n;
s: =0;
sn: =sn1;
s: =s+f (a) +f (b);
for i: =1 to (n-1) do
s: =s+2*f (a+i*h);
s: = (h/2) *s;
sn1: =s;
until abs (sn-s) <e;
writeln ('s=',s: 8: 3);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 s=0.117
Задание 3. Решение системы линейных уравнений
Решение уравнения с помощью MathCAD
Данная задача в MathCAD будет выполнятся с использованием ранжированной переменной. В среде пакета MathCAD для выполнения итеративных вычислений предусмотрен аппарат ранжированных переменных.
Ранжированная переменная-это переменная, которой приписан диапазон изменения значений.
Пример ранжированной переменной:
x: = a, b. c,
где x - переменная, a,b,c - значения, которые принимает переменная, т.е. a-первое значение, b-второе значение, т.е. (b-a) - шаг изменения переменной, и c-последнее значение. .
Рассмотрим решение системы линейных уравнений матричным методом:
a11 X1 +a12 X2 +a13 X3 =b1, a21 X1 +a22 X2 +a23 X3 =b2, a31 X1 +a32 X2 +a33 X3 =b3 .
Решение этим методом заключается в решении матричного уравнения вида:
R=M-1 *V.
Для этого необходимо:
сформировать матрицу коэффициентов системы линейных уравнений
сформировать вектор-столбец коэффициентов свободных членов системы линейных уравнений V:
b1
V: = b2
b3
найти искомые параметры с помощью матричного уравнения: R=M-1 *V.
получим:
X1
R = X2
X3
Рассмотрим решение системы линейных уравнений с помощью решающего блока Given - Find.
Для решения системы уравнений этим способом используется специальная конструкция, называемая решающим блоком . Блок состоит из заголовка (Given ), его тела (определённой системы уравнений) конца блока (Find ). Find включает в себя перечень переменных блока, относительно которых должна быть решена система уравнений.
Для решения этим методом введём начальные приближённые значения искомых значений:
X1: =0X2: =0X3: =0
опишем блок решения:
Given
x11 X1 +x12 X2 +x13 X3 =b1, x21 X1 +x22 X2 +x23 X3 =b2, x31 X1 +x32 X2 +x33 X3 =b3 .
опишем ведущие переменные:
r: =find (X1, X2, X3)
найдём искомые параметры:
X1
r = X2
X3
Пример вычисления:
1) решение системы линейных уравнений матричным методом:
![]()
![]()
![]()


![]()

2) решение системы линейных уравнений с помощью решающего блока Given - Find.
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()

Задание 4. Решение нелинейного уравнения
Задача нахождения корней нелинейных уравнений вида F (x) =0 встречается в различных областях научных исследований. Нелинейные уравнения можно разделить на два класса - алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.
По условию задачи уравнение cosx-x+4=0 является трансцендентным. Поэтому для нахождения корней будем использовать приближённые методы вычисления (метод касательных и метод половинного деления).
Существуют различные итерационные методы решения трансцендентных уравнений. Наиболее известные: метод касательных, метод половинного деления, метод хорд, комбинированный метод хорд и касательных, метод итераций и т.д.
Метод половинного деления отрезка пополам является одним из простейших методов нахождения корней нелинейных уравнений. Метод довольно медленный, однако он всегда сходится, т.е. при использовании решение получается всегда, причём с заданной точностью. Требуемое обычно большее число итераций по сравнению с некоторыми другими методами не является препятствием к применению этого метода, если каждое значение функции несложно.
Метод касательных или метод Ньютона. В этом методе каждой итерации объём вычислений больший, чем в ранее рассмотренном методе половинного деления, поскольку приходится находить не только значение функции F (x), но и значения её производных. Однако скорость сходимости здесь значительно выше, чем в предыдущем методе.
Решение нелинейного уравнения в среде пакета MathCAD
По условию задачи данное нелинейное уравнение является трансцендентным. Для нахождения корней этого уравнения воспользуемся функцией root.
![]()
![]()

![]()
![]()
![]()
Решение трансцендентных уравнений методом касательных
program kasatelnie;
uses crt;
label 20;
var a,b,E,U,D,x: real;
function f (x: real): real;
begin
f: =u*u*u-7*u-7;
end;
function f1 (x: real): real;
begin
f1: =3*x*x-10;
end;
function f2 (x: real): real;
begin
f2: =6*x;
end;
begin
writeln ('a,b,E=');
read (a,b,E);
if f (a) *f2 (a) >0 then
u: =a else u: =b;
20: D: =f (u) /f1 (u);
u: =u-d;
if ABS (d) >E then goto 20;
writeln ('u=',u: 7: 3);
readkey;
end.
Результаты работы программы
a=2 b=4 e=0.01 x=3.000
Блок-схема алгоритма решения задания №4.2
Метод касательных:
Решение трансцендентных уравнений методом деления отрезка пополам
Program polovinoedelenie;
uses crt;
label 20,30,40;
var a,b,E,V,W,X,Z: real;
function f (x: real): real;
begin
f: =x*x*x-7*x-7;
end;
begin
writeln ('a,b,E=');
read (a,b,E);
V: =f (a);
W: =f (b);
20: x: = (a+b) /2;
z: =f (x);
if z=0 then goto 30;
if V*Z>=0 then
begin
a: =x;
v: =z;
end;
begin
b: =x;
W: =z;
end;
40: if (b-a) >E then goto 20;
x: = (a+b) /2;
30: writeln ('x=',x: 6: 3);
readkey;
end.
Результаты работы программы
a=2 b=4 e=0.01 u=3.049
Блок-схема алгоритма решения задания №4.1
Метод деления отрезка пополам:
Задание 5. Организация нахождения минимума и максимума элемента в массиве случайных чисел в среде пакета MathCAD
Организовать нахождение MIN и MAX элемента в массиве случайных чисел К. Генерацию элементов массива осуществить с помощью встроенной функции RND (N); вычисления провести с помощью встроенных функций MIN (К) и MAX (К)
В Mathcad:
Необходимое нахождение значений в среде MathCAD можно провести с помощью встроенных функций.
Для решения этой задачи нужно: задать промежуток, в котором будут генерироваться случайные числа; воспользоваться функцией rnd; после того, как будут выбраны случайные числа, воспользуемся функцией нахождения минимального и максимального значений: min (x) и max (x).
![]()
![]()
![]()
![]()

Задание 6
Определить среднее арифметическое, среднее квадратическое отклонение рядов Ni и Ki , дисперсию и коэффициент корреляции. Ввод Ni и Ki -в виде векторов из 10 элементов, каждый из внешних файлов данных, подготовленных вручную или с помощью любой программы, позволяющей создавать файлы в формате ASCIT. Вычисление - с помощью встроенных функций: mean (N), mean (K), var (N), var (K),stdev (K), stdev (K), corr (N,K).
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
Похожие рефераты:
Решение обратной задачи вихретокового контроля
Высшая математика для менеджеров
Разностные схемы для уравнения переноса на неравномерных сетках
Производная и ее применение в алгебре, геометрии, физике
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ)
Методы решения уравнений, содержащих параметр
Сравнительный анализ алгоритмов построения выпуклой оболочки на плоскости


