| Скачать .docx |
Курсовая работа: Применение симплекс-метода
Содержание:
Введение …………………………………………………..
Постановка задачи
Описание метода
Математическая постановка задачи …………………….
Листинг программы………………………………………..
Блок-схема………………………………………………….
Заключение…………………………………………………
Список литературы………………………………………..
Введение
Целью данной курсовой работы является решение конкретной задачи линейного программирования методом улучшенного симплекс-метода. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Для решения задач линейного программирования созданы специальные методы. Изучению одного из них, а именно улучшенному симплекс-методу, посвящена эта курсовая работа.
Постановка задачи
На основе изученного алгоритма симплекс-метода разработать программу по следующему заданию: Исходная матрица коэффициентов заносится в память как матрица А, правые части ограничений заносятся в столбец 0. Таким образом, в матрицу входят М+2 строк, М ограничений, целевая функция и искусственная целевая функция. Она имеет P строк помимо строки 0, которые содержат исходные, новые и искусственные переменные. Матрица B состоит из столбцов значений переменных и значений целевой функции, матрицы обращения размерностью m x m, двух строк симплекс - множителей и последнего столбца, в котором все элементы, кроме последних двух, равны 0, а последние два равны – 1:
b́1 β11 β 1m 0
b΄2 β21 β 2m 0
B= b́m βm1 β mm 0
-z΄0 π1 πm 1
-ẃ0 ơ1 ơ m 1
Необходимо перевести данную программу с помощью языка Turbo Pascal .
Для проверки работоспособности программы необходимо ввести данные из следующего задания:
Найти такие неотрицательные x1 , x2 , что
2х1 – х2 ≤ 4,
x1 – 2x2 ≤ 2,
x1 + x2 ≤ 5,
и минимизировать функцию -3x1 + x2 = z.
Сделаем несколько замечаний относительно преимуществ и недостатков улучшенного симплекс-метода и симплекс-метода. При использовании улучшенного симплекс-метода исходная матрица ограничений запоминается. В симплекс методе ее элементы меняются при прохождении итераций. Таким образом, поскольку в улучшенном симплекс-методе нужны также обращение базиса и симплекс - множители, недостатком улучшенного симплекс-метода является большая потребность в машинной памяти.
Большим преимуществом улучшенного симплекс-метода является уменьшение количества вычислений. Таким образом, количество вычислений в задаче линейного программирования напрямую связано, скорее, с количеством ограничений, чем с количеством переменных, которые в общем случае значительно больше.
Улучшенный симплекс-метод непосредственно вычисляет обращение базиса и симплекс - множители. Эти величины не надо извлекать из окончательной таблицы. Это может помочь при последующем устойчивости решения.
Описание метода
Для решения задач линейного программирования существует множество методов. Рассмотрим один из них.
Улучшенный (модифицированный) симплекс-метод
Для начала расскажем, что такое симплекс-метод. Слово SIMPLEX в обычном смысле означает простой, несоставной, в противоположность слову COMPLEX.
Данный метод получил несколько различных форм (модификаций) и был разработан в 1947 году Г. Данцигом.
Сущность симплекс-метода заключается в том, что если число неизвестных больше числа уравнений, то данная система неопределенная с бесчисленным множеством решений. Для решения системы все неизвестные произвольно подразделяют на базисные и свободные. Число базисных переменных определяется числом линейно-независимых уравнений. Остальные неизвестные свободные. Им придают произвольные значения и подставляют в систему. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, которые дадут бесчисленное множество решений. Если все свободные неизвестные приравнять к нулю, то решение будет состоять из значений базисных неизвестных. Такое решение называется базисным.
В теории линейного программирования существует теорема, которая утверждает, что среди базисных решений системы можно найти оптимальное, а в некоторых случаях и несколько оптимальных решений, но все они обеспечат экстремум целевой функции. Таким образом, если найти какой-либо базисный план, а затем улучшить его, то получится оптимальное решение. На этом принципе и построен симплекс-метод.
Одним из модификаций симплекс-метода является улучшенный симплекс-метод.
В литературе этот метод встречается также под названием метода обратной матрицы или модифицированного симплекс-метода.
При решении задач линейного программирования, в которых n (количество переменных) существенно больше m (количество ограничений), улучшенный симплекс-метод требует по сравнению с другими значительно меньшего количества вычислительных операций и объема памяти ЭВМ.
В улучшенном симплекс-методе реализуется та же основная идея, что и в обычном симплекс-методе, но здесь на каждой итерации пересчитывается не вся матрица A-1 , обратная матрице ограничений A, а лишь та часть, которая относится к текущему базису Ax .
Рассмотрим поэтапно шаги решения задачи линейного программирования улучшенным симплекс-методом:
1.В начале первого цикла нам известны обратная матрица (единичная матрица), базисное решение xb = b.
2.Образуем для каждой небазисной переменной характеристическую разность Dj , используя уравнение:
Dj = cj — = cj — pPj ,
Где p - двойственные переменные, которые можно найти следующим образом:
p = cx * ,
Где cx - вектор коэффициентов целевой функции при базисных переменных.
3.Предполагая, что используется стандартное правило выбора вводимого столбца, находим:
.
4.Если Ds ³ 0 - процедура останавливается. Текущее базисное решение является оптимальным.
5.Если Ds £ 0, вычисляем преобразованный столбец:
= Ps
6.Пусть
= (, , ..., ) .
Если все £ 0 - процедура останавливается: оптимум неограничен.
7.В противном случае находим выводимую из базиса переменную:
= q .
8.Строим увеличенную матрицу:
-1;\s\do(x:;:;:
и трансформируем ее с ведущим элементом . Первые m столбцов результат дают матрицу, обратную новому базису. Преобразуем базисное решение:
xb i Ü xb i — q * , i ¹ r,
xb r Ü q
и переходим к этапу 2.
Этот вариант называют также модифицированным симплекс-методом, поскольку он уменьшает объем вычислений на каждом шаге. Идея заключается в том, что на каждом шаге конаническую форму задачи для текущего базиса можно получить независимо от других таких форм непосредственно из исходной записи стандартной задачи ЛП. Для этого нужно: (1) сохранять исходную запись задачи на протяжении всей работы метода, это та цена, которую приходится платить за больше быстродействие;
(2) использовать так называемые симплекс – множители π – коэффициенты для непосредственного перехода от исходной записи задачи к ее текущей конанической форме базиса; и (3) использовать обращенный базис В־¹ - матрицу размера m x m, позволяющую вычислять на каждом шаге ведущий столбец a΄s и обновлять симплекс – множители π.
Преимущества метода
Улучшенный симплекс-метод, обладает значительными преимуществами по сравнению со стандартной формой. Это относится к точности, скорости и требованиям к памяти. Большая часть этих преимуществ определяется тем фактором, что, как правило, матрицы больших линейных задач (то есть с n>m>100) являются слабозаполненными, содержат малый процент ненулевых элементов.
Обычной является плотность 5% или менее. Улучшенная форма симплекс-метода в большей степени способна использовать преимущества, вытекающие из этого факта. В этой форме характеристические разности и ведущий вектор вычисляются непосредственно по исходным данным. Поскольку исходная матрица слабозаполнена, а перемножение следует производить только тогда, когда оба сомножителя отличны от нуля, то время вычислений значительно сокращается.
В дополнение к этому использование только исходных данных приводит к тому, что уменьшается возможность накопления ошибок округления. Наоборот, стандартные симплексные таблицы, даже если они первоначально являются слабозаполненными, в ходе итеративного процесса быстро заполняются ненулевыми элементами. Таким образом, время вычислений увеличивается, и, поскольку каждая таблица вычисляется из предшествующей, накопление ошибок может начать играть более серьезную роль.
Математическая постановка задачи
Задание: Найти такие неотрицательные x1, x2, что
2х1 – х2 ≤ 4,
x1 – 2x2 ≤ 2,
x1 + x2 ≤ 5,
и минимизировать функцию -3x1 + x2 = z.
Графическое решение (см. рисунок) показывает, что точка минимума – это точка (3,2), где z = -7. Вырожденность (при обращении нескольких переменных в 0, базис называют вырожденным) возникает, поскольку прямые, соответствующие ограничениям, пересекаются в одной точке (2,0). В нашей задаче в вершине пересекаются три прямые (обычно вершина является пересечением всего двух прямых).
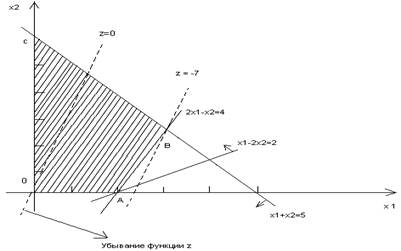
Рисунок 1.
При использовании симплекс-метода первая таблица имеет следующий вид:
Таблица 1.
| Итерация |
Базис |
Значение |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
| 0 |
Х3 Х4 Х5 |
4 2 5 |
2* 1* 1 |
-1 -2 1 |
1 . . |
. 1 . |
. . 1 |
| -z |
Целевая функция |
-3 |
1 |
. |
. |
. |
Переменная х1 входит в базис. В столбце х1 коэффициенты 2 и 1 пометим звездочкой, так как в точке минимума они имеют точку совпадения 4/2 = 2/1.
При выборе других переменных все равно итерация превращается в 0, следовательно, базис будет вырожден. Выберем переменную х3 и получим следующую таблицу:
Таблица 2.
| Итерация |
Базис |
Значение |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
| 1 |
Х3 Х4 Х5 |
2 0 3 |
1 . . |
-1/2 -3/2 3/2* |
1/2 -1/2 -1/2 |
. 1 . |
. . 1 |
| -z |
6 |
. |
-1/2 |
3/2 |
. |
. |
|
| 2 |
Х1 Х4 Х2 |
3 3 2 |
1 . . |
. . 1 |
1/3 -1 -1/3 |
. 1 . |
1/3 1 2/3 |
| -z |
7 |
. |
. |
4/3 |
. |
1/3 |
Из таблицы видно что минимум функции z равен -7 (при х1 = 3, х2 = 2).
Если выбрать переменную х4, то получим то же самое решение.
Для продолжения решения необходимо изменить ограничения, это позволит изменить положение точки А, а так же избежать вырожденности. Для это возьмем некоторую переменную ε – малая величина (т.к. ограничения в точке А не будут выполняться одновременно, см. рисунок 2).
Получим следующее:
2х1 – х2 ≤ 4+ ε
x1 – 2x2 ≤ 2+ ε2 .
В окончательное решение будет входить ε. Затем ε следует обратить в 0.
Если вырожденности нет, то симплекс-методом задача линейного программирования решается за конечное число шагов (при условии что решение существует).
Таким образом, функция z убывает на каждом шаге. Поскольку имеется не более (n/m) допустимых решений, минимум будет равен не более чем за (n/m) итераций.
Листинг программы
{ Reshenie zadachi lin prog-ya modifiz simplex-metodom }
Program Simpl_ST;
uses crt;
label 500, 1800, 1900, 2000, Zikl,{} 2500, 1960;
const M1_K = 30; M2_K = 30; P_K = 30; M_K = 30;
var i, j, k, zz, GC, EC, LC, N, MM, M, MK, N1, P, M1, M2, N0: integer;
A: array[1..M2_K,0..P_K] of integer;
B: array[1..M2_K,0..M1_K] of integer;
BS: array[1..M_K] of integer;
V: array[1..M2_K] of integer;
NB, SL, C: array[1..P_K] of integer;
PB, PA, L, ML, NI, SS: integer;
Zero, NILL, MIN, RT, DF: real;
S, PV, R: integer;
P_str, PE_str: string;
cc: integer;
Dop: boolean;
buf:array[1..36] of byte absolute 0:$41a;
procedure clearkeybuf;{ ochistka bufera klaviatury}
begin
inline($fa); {cli - preryvaniya nado zapretit pri }
buf[1] := buf[3]; { vmeshatelstve v bufer }
inline($fb); {sti }
end;
procedure Init;
begin
for i:=1 to M2_K do for j:=0 to P_K do A[i,j]:=0;
end;
function DelZero(X: Real): string;{Udalenie nulei posle zapyatoi}
var i, l, sp: integer;
Drob, Space: boolean;
Xst, Res: string;
begin
Xst:=''; Drob:=False;
Str(X:13:10, Xst);
for i:=1 to Length(Xst) do if Xst[i]='.' then Drob:=True;
if Drob then begin
for i:=Length(Xst) downto 1 do begin
if Xst[i]='0' then Xst[i]:='Z';
if Xst[i]='.' then begin Xst[i]:='Z'; Break end;
if Xst[i] in ['1'..'9'] then Break;
{case XS[j] of
'0': XS[j]:='Z';
'.': XS[j]
1..9: Break;
end; }
end;
for i:=1 to Length(Xst) do if Xst[i]='Z' then begin l:=i;Break end;
Res := Copy(Xst,1,l-1);
end
else Res := Xst;
Space := False;
for i:=1 to Length(Res) do if Res[i]=' ' then
begin l:=i; Space := True end; {del spaces}
if Space then Res := Copy(Res,l+1,Length(Res)-l);
{sp:=0;
for i:=1 to Length(Res) do begin
if Res[i] = ' ' then inc(sp);
end;
if (X>=0)and(sp=0) then Res := ' ' + Res; }
if X >= 0 then Res := ' ' + Res;
DelZero := Res;
end;
procedure Gosub9000;
var PE, PEint: real;
PC, PD: integer;
MID, RIGHT: string;
begin
PC := round(int(PB/100));
P_str:='';
if PC=0 then write(' ') else write(Copy(P_str,1,PC)); { LEFT$(P$,PC) }
PC := PB - 100*PC;
PD := round(int(PC/10));
PC := PC - 10*PD;
if PD = 0 then PD := 1;
if PA < 0 then P_str := P_str+'-';
PE := abs(PA); { A^X=EXP(X*LN(A)) }
PE := PE + 5 * EXP((-1-PC)*LN(10)); { PE := PE + 5*10^(-1-PC) }
if PE >= EXP(PD*LN(10)) then begin write(PA); Exit end; { PE>=10^PD }
{Str(PE:13:10, PE_str); { Copy(Str,1,N); Left }
PEint := int(PE);
PE_str:=DelZero(PEint);
MID := Copy(PE_str,2,PD);{ MID$(PE_str,2,PD) }
P_str := P_str + MID;
{PRINT RIGHT$(P$,PD+1)}
RIGHT := Copy(P_str,Length(P_str)-(PD+1)+1,PD+1);
GotoXY(WhereX+3,WhereY);
write(RIGHT); { RIGHT$(P$,PD+1) Copy(Astr,Length(Astr)-N+1,N); Right }
if PC = 0 then Exit;
write('.');
PE:=int((PE-int(PE)) * EXP(PC*LN(10)));
P_str:='000000000';
PE_str:=DelZero(PE);
{PE_str := KillZero(PE_Str);}
{P_str:=P_str+Copy(KillZero(PE_str),2,PC);}
MID := Copy(PE_str,2,PC);
P_str := P_str + MID;
RIGHT := Copy(P_str,Length(P_str)-PC+1,PC);{RIGHT(P$,PC) }
write(RIGHT,' ');
end;
procedure Gosub3000;
begin
write('Bazis Znachenie ');
for j:=1 to N+3 do write(' X',j,' ');
writeln;
PB := 122;
for i:=1 to ML do begin
if i=M1 then write(' tselev func');
if i=M2 then write(' iskust func');
if (i<>M1)and(i<>M2)then begin write(' ',i,' '); PA:=A[i,0]; Gosub9000 end;
for j:=0 to N0 do begin
PA:=A[i,j];
Gosub9000;
end;
writeln(' ');
end;
write(' ');
end;
procedure Gosub3500;
begin
If L=1 then writeln('ETAP 1 vsyo esho prodolzhaetsya');
PB:=122;
for j:=1 to N0 do write(' C',j,' ');
writeln;
for j:=1 to N0 do begin PA:=C[j]; Gosub9000 end;
writeln;
if SS<>1 then writeln('X',S,' Vhodit B,X',BS[R],' v uslovii ',R,' vyveden iz bazisa');
writeln('Bazis Znachenie Obrashenie Bazisa');
if SS=1 then write(' ');
{write(' A'iS');}
for i:=1 to ML do begin
if i=M1 then write('Reshenie dlya tselevoy functii');
if i=M2 then write('Reshenie dlya iskustven functii');
if (i<>M1)and(i<>M2) then write(' ',BS[i]);
for j:=0 to M do begin
PA:=B[i,j];
Gosub9000;
end;
if SS<>1 then begin PA:=V[i]; Gosub9000 end;
writeln(' ');
end;
writeln(' ');
end;
begin
clearkeybuf;
Init;
textbackground(0); textcolor(15);
clrscr;{promezhut tablitsa pri zz = +1 vyvod, -1 net }
writeln('Reshenie zadachi lin prog-ya simplex-metodom');
{write('Vvedite zz '); readln(zz);} zz:=1;
{Vvesti kol-vo vidov ogranicheniy i kolvo peremennyh}
{write('Vvedite cherez probel GC, EC, LC, N ');
Readln(GC, EC, LC, N); { 2, 0, 2, 2 }
GC:=0; EC:=0; LC:=3; N:=2;
MM:=GC+EC; M:=MM+LC; MK:=GC+LC; N1:=MK+N;
P:=N1+MM; M1:=M+1; M2:=M+2; N0:=N1;
{Vvesti koeff-ty dlya ogranicheniy i tselevoy functii}
{matriza: vvodit stroku matrizy cherez probel,v konze stroki press Enter}
{writeln('Input matrix ',M1, 'x', N);
for i:=1 to M1 do begin
for j:=1 to N do read(A[i,j]);
readln;
end; }
A[1,1]:=1; A[1,2]:=-2; A[2,1]:=2; A[2,2]:=-1; A[3,1]:=1; A[3,2]:=1;
A[4,1]:=-3; A[4,2]:=1; {A[5,1]:=0; A[5,2]:=0; }
{ vyvod matrix na ekran }
writeln('Matrix ',M1,'x',N);
for i:=1 to M1 do begin
for j:=1 to N do write(A[i,j],' ');
writeln;
end;
cc := 0;
{Zadat oslablennye, iskustvenye peremennye, pometit bazis i vvesti
peremennye v nulevoi stolbez}
writeln('Zadaite oslablennye, iskustvennye peremennye'); { 10, 5, 20, 20 }
if GC <> 0 then begin
for i:=1 to GC do begin {1 2}
A[i,N+1]:=-1; A[i,N1+i]:=1; B[M2,i]:=-1;
B[i,i]:=1; A[M2,N1+i]:=1; BS[i] := N1+i;
write(' ? ');read(A[i,0]); B[i,0]:=A[i,0]
{ if i=1 then A[i,0]:=10;
if i=2 then A[i,0]:=5; }
{ inc(cc) }
end
end;
if EC <> 0 then begin
for i:=GC+1 to MM do begin
A[i,N1+i]:=1; B[i,i]:=1; A[M2,N1+i]:=1;
BS[i]:=N1+i; B[M2,i]:=-1; write(' ? ');read(A[i,0]);
B[i,0]:=A[i,0]
{inc(cc); }
end;
end;
if LC <> 0 then begin
for i:=MM+1 to M do begin {3 4}
A[i,N+i-EC]:=1; B[i,i]:=1; BS[i]:=N+i-EC; write(' ? '); read(A[i,0]);
B[i,0]:=A[i,0]
{ if i=3 then A[i,0]:=20;
if i=4 then A[i,0]:=20; }
{inc(cc);}
end;
end;
if MM = 0 then writeln('Otsutstvuet ETAP 1 resheniya zadachi ');
{writeln(cc);}
{Zadat iskustvenuyu function for ETAP 1 }
L := 1; N0 := P; { N0 yavlyaetsya nomerom nuzhnogo stolbza }
for i:=1 to MM do B[M2,0] := B[M2,0] - B[i,0];
ML:=M1+L; { ML=M+2 dlya ETAPA 1; ML=M+1 dlya ETAPA 2 }
if zz >= 0 then writeln('Pervonachalnaya tabliza');
Gosub3000;
{Repeat until keypressed;}
{ Vyhod iz progi }
{Pometit nebazisnye peremennye, NB[j]=0, esli j-nebazisnaya peremennaya}
for i:=1 to M do NB[BS[i]]:=1;
Zero := 0.00000001; NILL := 1E-20;
{Exit; { Halt(0) }
{ Naiti naimenshiy koef-t v stroke zelevoy functii, t.e. stroku ML }
500: MIN := -Zero; S:=0; PV:=0; ML:=M1+L;
for j:=1 to N0 do begin
C[j]:=0;
if NB[j] <> 1 then begin
{ Vychislit C[j] }
for i:=1 to M do C[j]:=C[j]+B[ML,i]*A[i,j];
C[j]:=C[j]+A[ML,j];
if C[j]<MIN then begin MIN:=C[j]; S:=j end
end
end;
{ Esli S = 0, to vse koef-ty polozhitelny i minimum naiden }
if S = 0 then goto 1900;
{ Naiti stroku peremennyh, kotoruyu sleduet iskluchit iz bazisa
po usloviyu minimuma BI/A'[iS] }
MIN := 1E20; R:=0;
{Vychislit A'[iS] i pomestit v stolbez V }
for i:=1 to M1 do begin
V[i]:=0;
for k:=1 to M1 do V[i]:=V[i]+B[i,k]*A[k,s]
end;
V[ML]:=C[S];
for i:=1 to M do begin
if V[i]<=Zero then Continue;
k:=0;
Zikl:
RT:=B[i,k]/V[i];
DF:=RT-MIN;
if DF<0 then begin
R:=i;
MIN:=B[i,0]/V[i];
Continue
end;
if DF<>0 then Continue;
k:=k+1;
MIN:=B[R,k]/V[R];
goto Zikl
end; {NEXT i}
{ Esli R = 0, to imeet mesto reshenie bez ogranicheniy }
if R = 0 then goto 1800;
if zz>=0 then Gosub3500;
Repeat Until keypressed; {pervoe reshenie}
{ Obnovit obratnyi i simplex- mnozhiteli }
PV := V[R];
for j:=0 to M1 do B[R,j]:=Round(B[R,j]/PV);
{ Perenaznachit B povtorno pometit bazisnye i nebazisnye peremennye }
NB[BS[R]]:=0; NB[S]:=1; BS[R]:=S; NI:=NI+1;
Goto 500;
1800: writeln('Peremennaya "S" ne imeet ogranicheniy ');
Gosub3500; readkey;
Goto 2500;
1900:if L=0 then Goto 2000;
{ Dlya ETAPA 2 eta tochka yavl-sya minimumom. Esli my nahodimsya na ETAPE 1,
to pereiti k ETAPU 2, proverit, chto W stalo ravno 0 }
if abs(A[ML,0]) >= 1E-08 then Goto 1960;
writeln('ETAP 1 uspeshno zavershon');
L:=0; N0:=N1; { Zadat L i nomer stolbza dlya ETAPA 2 }
Goto 500;
1960: writeln('Ogranicheniya ne imeyut dopustimogo resheniya');
writeln('summa iskustvennyh peremennyh ravna ',-B[ML,0]);
Gosub3500;
2000:writeln('Okonchatelnoe reshenie');
writeln('Ogranichenie Bazis Znachenie');
PB := 144;
for i:=1 to M do begin
SL[BS[i]]:=B[i,0];
write(' ',i,' ',BS[i],' ');
PA:=B[i,0];
Gosub9000;
writeln(' ');
end;
writeln('Minimum functii Z raven ',-B[M1,0]);
writeln('Ogranichenie Sostoyanie Dopolnitelnye peremennye');
for i:=1 to M do begin
Dop:=False;
write(' ',i,' ');
if (i>GC)and(i<=MM) then begin write('Uravnenie ne resheno');Continue end;
if NB[N+i]=1 then begin write(' dopoln.perem. '); Dop:=True end;
PA:=SL[N+i];
Gosub9000;
write(' '); {Continue; }
if not Dop then begin gotoXY(whereX-8,WhereY);writeln('Ogranichenie 0') end else writeln;
end; writeln;
SS:=1;
Gosub3500;
2500:writeln('The End.');
Clearkeybuf;
Repeat until keypressed
end.
Блок-схема
 |
( Примечание: Если ММ=0,
то отсутствуетЭТАП 1)
 |
(Примецание: Начало решения)
 |
Заключение
Данный курсовой проект был первым, необходимым для закрепления навыков в умении программировать. Здесь были заложены основы математических методов решения задач. Будущей специализацией курсового проекта являлось разработка программы на языке TURBO PASCAL. Поэтому большее внимание уделялась следующим разделам:
· Основы математических методов и их применение;
· Решение задач с помощью улучшенного симплекс – метода;
· Основы программирования (язык Turbo Pascal).
Пользователю предлагается ввести расчетные данные, чтобы получить конкретные характеристики.
Программа разработана на языке Turbo Pascal 7.0, что предполагает минимальные системные требования для работы с ней.
Список литературы
1. Акулич И.Л. Матеиатическое программирование в примерах и задачах: Учеб. Пособие для студ. Вузов. – М.: Высш. Шк., 1986.
2. Банди Б. Основы линейного программирования /пер. с англ. Под ред. В.А. Волынского. – М.: Радио и связь, 1989.
3. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика: Математическое программирование. – Минск: Высшая школа, 1994.