Главная / Рефераты / Информатика, программирование

Курсовая работа: Обработка информации и принятие решения в системах ближней локации

Курсовая работа

по дисциплине: «Теория обработки информации в системах ближней локации»

на тему: «Обработка информации и принятие решения в системах ближней локации»

Содержание

Задание на курсовое проектирование

Введение

Исходные данные

1. Исследование вероятностной структуры сигналов

1.1 Построение гистограмм выборочных плотностей вероятности амплитуд сигналов, как случайных величин

1.2 Изучение законов распределения случайных величин

1.3 Оценка параметров распределения случайных величин для четырех законов

1.4 Построение на одном графике теоретического и практического распределения для формулировки гипотезы

1.5 Проверка гипотезы по критерию Колмогорова – Смирнова

1.6 Проверка гипотезы по критерию согласия Пирсона

1.7 Построение корреляционной функции для фрагмента сигнала длительностью 2000 отсчетов

2. Формирование обучающих и контрольных множеств данных

2.1 Признаки по оценке плотности распределения вероятности в пяти интервалах положительной области

3. Исследование признаков

3.1 Оценка параметров распределения признаков. Определение информативного признака с максимальным расстоянием, построение функций плотности распределения вероятностей и вычисление порога принятия решения, формулирование решающего правила

4. Обучение двухслойной нейронной сети

4.1 Общие сведения о нейронных сетях

4.2 Обучение нейронной сети

Заключение

Список использованных источников

Исходные данные

Задача обнаружения гусеничной техники, проезжающей на расстоянии 200 м от сейсмоприемника. Сигналы fon и tr_t200 предназначены для обучения и контроля нейронной сети. Сигнал test_t50 – для тестирования работы нейронной сети. Признаки: распределение мощности в десяти равномерных интервалах (по 25 гармоник).

Рисунок 1 – Исходный фоновый сигнал

Рисунок 2 – Исходный сигнал гусеничной техники

Введение

За последние 10…20 лет существенно расширилась область использования технических средств охранной сигнализации (ТСОС): они используются для охраны, как военных объектов, атомных станций, государственной границы, так и дачных и фермерских хозяйств. Возрастают и требования к ТСОС по энергопотреблению и габаритным размерам, быстродействию и эффективности, кругу решаемых задач.

Ранее в основном решалась задача обнаружения нарушителя с вероятностью 0.9, в настоящее время требуется повысить вероятность до 0.95 и более при снижении времени наработки до ложной тревоги с 1000 до 2000 часов (вероятности ложной тревоги). Все чаще ставятся задачи распознавания нарушителя по классам человек-группа людей, колесная-гусеничная техника с вероятностью 0.8…0.9 и определения места и направления пересечения охраняемого рубежа или зоны.

Для решения поставленных задач недостаточно простых схемотехнических решений и алгоритмов, основанных на амплитудно-временной селекции сигналов.

Анализ отечественных и зарубежных ТСОС показал, что основным направлением их развития является разработка более сложных алгоритмов обработки сигналов, основанных на исследовании «тонкой» внутренней структуры сигналов, генерируемых нарушителем, и выявлении наиболее отличительных характеристик (признаков).

1. Исследование вероятностной структуры сигналов

1.1 Построение гистограммы

Различные законы распределения различаются видом графиков F (x ) и f (x ). Из математического анализа известно, что при интегрировании функции сглаживаются, а при дифференцировании, их особенности проявляются сильнее. Поэтому функция плотности распределения вероятности f (x ) содержит больше информации, чем функция распределения F (x ).

По определению плотность распределения f (x ) – это предел отношения вероятности попадания в малый интервал к ширине этого интервала, когда ширина стремится к нулю. Для выборки выборочная вероятность попадания в некоторый интервал – это отношение числа попаданий в интервал n_j к общему числу попаданий n . Если ее разделить на ширину интервала h , то при малых h мы и получим выборочную плотность распределения:

(1)

Здесь мы не сможем использовать x_j поодиночке, их придется группировать по участкам. Поэтому вначале весь интервал изменения данных нужно разбить на участки одинаковой длины. Сколько участков взять? Есть несколько подходов к определению числа участков разбиения k . Один из них – это использование формулы Стэрджесса:

, (2)

где n – объем выборки, а – операция округления до ближайшего целого. Другой подход состоит в следующем. С одной стороны, число участков разбиения должно быть как можно больше, с другой стороны, в каждый из этих участков должно попадать как можно больше значений x_i . Компромисс между этими требованиями приводит к тому, что обычно выбирают число участков k для построения гистограммы как ближайшее целое к корню квадратному из n :

. (3)

После разбиения на k участков подсчитываем число попаданий в каждый из них n_j .

Из (1) следует, что гистограмма с точностью до множителя nh совпадает с графиком выборочной плотности распределения . Разделив ординаты гистограммы на nh , мы получим график .

Для построения гистограммы в MATLAB имеется функция hist . Она автоматически разбивает интервал изменения выборки на нужное количество участков, подсчитывает n_j и строит график.

Продолжим выполнение задания «Обработка массива данных». В нижеприведенной области ввода первая строка – это определение числа участков k . Сейчас здесь стоит . Если вы хотите использовать формулу Стэрджесса, измените эту строку. Определим ширину каждого интервала h (идентификатор d в программе). Построим гистограмму распределения (1).

Практическая часть .

clearall% очистили рабочую область

x=tr_t200; % вводим ИД

x=sort(x(:));% переформатировали столбец и рассортировали

n=length(x);% длина массива t_tr200

xmin=x(1);% находим минимальное значение

xmax=x(n);% находим максимальное значение

Mx=mean(x);% математическое ожидание

f=n-1;% число степеней свободы

Dx=var(x);% дисперсия

Sx=std(x);% среднеквадратичное отклонение

Ax=skewness(x);% асимметрия

Ex=kurtosis(x) – 3;% эксцесс

k=round(n^0.5);% число интервалов для построения гистограммы

d=(xmax-xmin)/k;% ширина каждого интервала

del=(xmax-xmin)/20;% добавки влево и вправо

xl=xmin-del;% левая граница интервала для построения гистограммы

xr=xmax+del;% правая граница интервала для построения гистограммы

fprintf('Число интервалов k=%d\n', k)

fprintf('Ширина интервала h=%14.7f\n', d)

figure% создаем новую фигуру

hist(x, k)% построили гистограмму

set(get(gcf, 'CurrentAxes'),…

'FontName', 'TimesNewRomanCyr', 'FontSize', 12)% установка типа и номера шрифта

title('\bfГистограмма')% заголовок

xlim([xlxr])% границы по оси OX

xlabel('\itx_{j}')% метка оси x

ylabel('\itn_{j}')% метка оси y

grid

Рисунок 3 – гистограмма распределения амплитуды сигнала гусеничной техники

Рисунок 4 – гистограмма распределения амплитуды фонового сигнала

Вывод: по виду полученных гистограмм можно сделать предположение о том, что распределение амплитуд сигнала подчиняется нормальному закону.

1.2 Изучение законов распределения случайных величин

Примеры распределений: нормальное, показательное (экспоненциальное), равномерное, рэлеевское

По виду гистограммы подбирается теоретический закон распределения. Для этого смотрим, на какую плотность распределения похожа гистограмма и выбираем соответствующий закон. В этом задании выбор небольшой. Мы рассматриваем только 4 наиболее часто встречающихся а приложениях законов распределения:

1. Нормальное.

2. Показательное (экспоненциальное).

3. Равномерное.

4. Рэлеевское.

Нарисуем с помощью MATLAB графики соответствующих плотностей распределения. Они показаны на рисунках 5 – 8. Здесь для вычисления f (x ) используется функция pdf , которая находит плотность любого из имеющихся в MATLAB видов распределений. Можно использовать и другой вариант: вычислять каждую плотность распределения с помощью своей функции: normpdf , exppdf и т.д.

Плотность нормального распределения – колоколообразная кривая, симметричная относительно некоторой вертикальной оси, но она может быть смещена по горизонтали относительно оси Оу . Значения х могут быть разного знака. Выражение для плотности нормального распределения имеет вид:

, (4)

а функция распределения:

, (5)

где Ф(u ) – интеграл Лапласа, для которого есть таблицы. Если считать функцию нормального распределения вручную, то удобно пользоваться таблицами интеграла Лапласа, которые есть в любом учебнике по теории вероятностей. При использовании MATLAB в этом нет необходимости: там есть функции normpdf и normcdf , а также функции pdf и cdf , в которых первый параметр (название распределения) должен иметь значение ‘norm ’ . В выражение для плотности и функции нормального распределения входят 2 параметра: m и s, поэтому нормальное распределение является двухпараметрическим. По нормальному закону обычно распределена ошибка наблюдений.

Плотность показательного распределения отлична от нуля только для неотрицательных значений х . В нуле она принимает максимальное значение, равное a. С ростом х она убывает, оставаясь вогнутой и асимптотически приближаясь к 0. Выражение для плотности показательного распределения:

(6)

а для функции распределения:

(7)

Показательно распределение является однопараметрическим: функция и плотность его зависят от одного параметра a.

Обратите внимание: в MATLAB параметр показательного распределения – это величина, обратная a в формулах (6 – 7).

Плотность равномерного распределения отлична от нуля только в заданном интервале [a , b ], и принимает в этом интервале постоянное значение:

(8)

Функция равномерного распределения левее точки а равна нулю, правее b – единице, а в интервале [a , b ] изменяется по линейному закону:

(9)

Равномерное распределение – двухпараметрическое, т. к. в выражения для F (x ) и f (x ) входят 2 параметра: а и b . По равномерному закону распределены ошибка округления и фаза случайных колебаний. В MATLAB плотность и функция равномерного распределения могут быть посчитаны с помощью функций unifpdf и unifcdf , а также с помощью функций pdf и cdf с первым параметром ‘unif ’.

Плотность рэлеевского распределения отлична от нуля только для неотрицательных значений х . От нуля она выпуклая и возрастает дол некоторого максимального значения. Далее с ростом х она убывает, оставаясь выпуклой. Затем становится вогнутой, продолжая убывать, и асимптотически приближается к 0. Выражение для плотности рэлеевского распределения имеет вид:

(10)

Функция рэлеевского распределения:

(11)

Это распределение однопараметрическое: оно зависит от одного параметра s. По рэлеевскому закону распределено расстояние от точки попадания в мишень до ее центра. Вычисление плотности и функции рэлеевского распределения в MATLAB реализовано с помощью функций raylpdf ,raylcdf или функцийpdf ,cdf с превым параметром ‘rayl ‘.

Практическая часть .

tdistr={'norm', 'exp', 'unif', 'rayl'};% названия

pardistr=[[2 1]; [2,0]; [0 4]; [1 0]];% параметры

ndistr=length(tdistr);% количество распределений

xpl=[-1:0.01:5]';% абсциссы для графиков

foridistr=1:ndistr, % заполняем и строим графики

ypdf=pdf (tdistr{idistr}, xpl,…

pardistr (idistr, 1), pardistr (idistr, 2));% ординаты

figure% новая фигура

plot (xpl, ypdf);% рисуем

set (get(gcf, 'CurrentAxes'),…

'FontName', 'Times New Roman Cyr', 'FontSize', 12)

title(['\bfПлотность распределения ' tdistr{idistr}])

end;

Рисунок 5 – плотность распределения амплитуды сигнала по нормальному закону

Рисунок 6 – плотность распределения амплитуды сигнала по экспоненциальному закону

Рисунок 7 – равномерная плотность распределения амплитуды сигнала

Рисунок 8 – плотность распределения амплитуды сигнала по Релеевскому закону

На практике могут встретиться и другие виды распределений (b, c² , логнормальное, Вейбулла и т.д.). Многие из них реализованы в MATLAB, но иногда приходится писать свои функции.

Графики некоторых плотностей распределения похожи между собой, поэтому иногда вид гистограммы позволяет выбрать сразу несколько законов. Если есть какие-либо теоретические соображения предпочесть одно распределение другому, можно их использовать. Если нет – нужно проверить все подходящие законы, а затем выбрать тот, для которого критерии согласия дают лучшие результаты.

1.3 Оценка параметров распределения случайных величин для четырех законов

В выражениях для плотности и функции нормального распределения (4 – 5) параметры m и s являются математическим ожиданием и среднеквадратичным отклонением. Поэтому, если мы остановились на нормальном распределении, то берем их равными, соответственно, выборочным математическому ожиданию и среднеквадратичному отклонению:

. (12)

Математическое ожидание показательного распределения есть величина, обратная его параметру a. Поэтому, если мы выбрали показательное распределение, параметр a находим:

(13)

Из выражений для m_x и s_x равномерного закона распределения находим его параметры a и b :

; . (14)

Параметр s рэлеевского распределения также находится из выражения для m_x

(15)

В системе MATLAB вычисление параметров теоретического распределения с помощью ПМП реализовано в функциях fit или mle . Подбор по методу моментов не реализован. Найдем параметры теоретического распределения по ПМП и методу моментов.

Практическая часть.

s={'нормальное распределение'; 'показательное распределение';…

'равномерное распределение'; 'Рэлеевское распределение'};

disp('Параметры по ПМП:')

[mx, sx]=normfit(x);% параметры нормального распределения

lam=1/expfit(x);% параметр показательного распределения

[a, b]=unifit(x);% параметры равномерного распределения

sig=raylfit(x);% параметр Рэлеевского распределения

fprintf([' % s: m=%12.7f; sigma=%12.7f\n'], s{1}, mx, sx)

fprintf (' % s: alpha=%12.7f\n', s{2}, lam)

fprintf (' % s: a=%12.7f; b=%12.7f\n', s{3}, a, b)

fprintf (' % s: sigma=%12.7f\n', s{4}, sig)

Для сигнала гусеничной техники :

Параметры по ПМП:

нормальное распределение: m= 0.0060038; sigma= 0.0203706

показательное распределение: alpha= 166.5608494

равномерное распределение: a= -0.0962308; b= 0.0942564

Рэлеевское распределение: sigma= 0.0150166

Для фонового сигнала:

Параметры по ПМП:

нормальное распределение: m= 0.0188599; sigma= 0.0005663

показательное распределение: alpha= 53.0224920

равномерное распределение: a= 0.0106122; b= 0.0210241

Рэлеевское распределение: sigma= 0.0133420

disp('Параметры по методу моментов:')

mx=Mx;

sx=Sx;% параметры нормального распределения

lam=abs(1/Mx);% параметр показательного распределения

a=Mx-Sx*3^0.5;

b=Mx+Sx*3^0.5;% параметры равномерного распределения

sig=abs(Mx)*(2/pi)^0.5;% параметр Рэлеевского распределения

fprintf([' % s: m=%12.7f; sigma=%12.7f\n'], s{1}, mx, sx)

fprintf (' % s: alpha=%12.7f\n', s{2}, lam)

fprintf (' % s: a=%12.7f; b=%12.7f\n', s{3}, a, b)

fprintf (' % s: sigma=%12.7f\n', s{4}, sig)

Для сигнала гусеничной техники :

Параметры по методу моментов:

нормальное распределение: m= 0.0060038; sigma= 0.0203706

показательное распределение: alpha= 166.5608494

равномерное распределение: a= -0.0292791; b= 0.0412867

Рэлеевское распределение: sigma= 0.0047903

Для фонового сигнала:

Параметры по методу моментов:

нормальное распределение: m= 0.0188599; sigma= 0.0005663

показательное распределение: alpha= 53.0224920

равномерное распределение: a= 0.0178790; b= 0.0198409

Рэлеевское распределение: sigma= 0.0150480

Вывод: из результатов, полученных двумя методами видно, что оценки плотностей распределения вероятностей для равномерного и рэлеевского законов по первому методу отличаются от плотностей распределения вероятностей по второму методу.

Оценки показательных и нормальных законов плотностей распределения вероятностей по обоим методам практически совпадают.

1.4 Построение на одном графике теоретического и практического распределения для формулировки гипотезы

Построим на одном графике теоретическую и эмпирическую плотности распределения вероятности. Эмпирическая плотность распределения – это гистограмма, у которой масштаб по оси ординат изменен таким образом, чтобы площадь под кривой стала равна единице. Для этого все значения в интервалах необходимо разделить на nh , где n – объем выборки, h – ширина интервала при построении гистограммы. Теоретическую плотность распределения вероятности строим по одному из выражений (4), (6), (8), (10), параметры для них уже вычислены. Эмпирическую плотность распределения нарисуем красной линией, а предполагаемую теоретическую – линией одного из цветов: синего, зеленого, сиреневого или черного.

Практическая часть.

[nj, xm]=hist(x, k);% число попаданий и середины интервалов

delta=xm(2) – xm(1);% ширина интервала

clearxfvfvxftft% очистили массивы для f(x)

xfv=[xm-delta/2; xm+delta/2];% абсциссы для эмпирической f(x)

xfv=reshape(xfv, prod(size(xfv)), 1);% преобразовали в столбец

xfv=[xl; xfv(1); xfv; xfv(end); xr];% добавили крайние

fv=nj/(n*delta);% значения эмпирической f(x) в виде 1 строки

fv=[fv; fv];% 2 строки

fv=[0; 0; reshape(fv, prod(size(fv)), 1); 0; 0];% + крайние, 1 столбец

xft=linspace(xl, xr, 1000)';% абсциссы для теоретической f(x)

ft=[normpdf (xft, mx, sx), exppdf (xft, 1/lam),…

unifpdf (xft, a, b), raylpdf (xft, sig)];

col='bgmk';% цвета для построения графиков

figure

plot (xfv, fv, '-r', xft, ft(:, 1), col(1), xft, ft(:, 2), col(2),…

xft, ft(:, 3), col(3), xft, ft(:, 4), col(4)) % рисуем

set (get(gcf, 'CurrentAxes'),…

'FontName', 'Times New Roman Cyr', 'FontSize', 12)

title('\bfПлотности распределения')

xlim([xlxr]), ylim([0 1.4*max(fv)])% границы рисунка по осям

xlabel('\itx')% метка оси x

ylabel('\itf\rm(\itx\rm)')% метка оси y

grid

Рис. 9 – График плотности распределения вероятности сигнала гусеничной техники и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности

Рис. 10 – График плотности распределения вероятности фонового сигнала и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности

Вывод: из рисунка 9 видно, что наиболее подходящим теоретическим распределением для первой эмпирической гистограммы является нормальное.

Реальный закон распределения амплитуд фонового сигнала также подчиняется нормальному закону.

1.5 Проверка гипотезы по критерию Колмогорова-Смирнова

Мы подобрали вид теоретического распределения и его параметры. Следующий этап – это проверка правильности подбора. Необходимо выяснить: насколько хорошо теоретическое распределение согласуется с данными. С этой целью используются критерии согласия Колмогорова-Смирнова или Пирсона., во втором – f (x ) и f ^* (x ).

Критерий согласия Колмогорова. В этом случае сравниваются теоретическая F (x ) и выборочная F ^* (x ) функции распределения. Сравниваемым параметром является максимальная по модулю разность между двумя функциями

. (16)

С точки зрения выборочного метода F ^* (x ) является случайной функцией, так как от выборки к выборке ее вид меняется, поэтому величина D является случайной. Согласно теореме Гливенко-Кантелли с ростом объема выборки эта величина сходится к нулю. Колмогоров А.Н. выяснил, как именно D сходится к нулю. Он рассмотрел случайную величину

(17)

и нашел ее закон распределения. Как оказалось, при достаточно больших n он вообще не зависит от закона распределения генеральной совокупности X . Причем функция распределения случайной величины L имеет вид

. (18)

Если опытные данные x действительно взяты из генеральной совокупности с функцией распределения F (x ), то вычисленная по выражению (18) реализация l случайной величины L на уровне значимости q должна лежать в квантильных границах распределения Колмогорова (18). При этом, если l малое (выходит за «левый» квантиль), то нулевая гипотеза принимается: теоретическое распределение согласуется с опытными данными. В общем случае нулевая гипотеза принимается, если выполняется условие

l £ l_1- _q . (19)

Данный критерий называется еще критерием Колмогорова-Смирнова.

Таким образом, для применения критерия согласия Колмогорова-Смирнова, мы должны найти максимальную по модулю разность между выборочной и теоретической функциями распределения D по выражению (16), вычислить по ней l и проверить условие (19).

Практическая часть.

param=[[mxsx]; [lam 0]; [ab]; [sig 0]];% параметры распределений

qq=[];% критические уровни значимости

foridistr=1:ndistr, % критерий Колмогорова

[hkolm, pkolm, kskolm, cvkolm]=…

kstest(x, [xcdf(tdistr{idistr}, x,…

param(idistr, 1), param(idistr, 2))], 0. 1,0);

qq=[qqpkolm];% критические уровни значимости

end

[maxqq, bdistr]=max(qq);% выбрали лучшее распределение

fprintf(['Лучше всего подходит % s;\nкритический уровень '…

'значимости для него =%8.5f\n'], s{bdistr}, maxqq);

figure

cdfplot(x);% эмпирическая функция распределения

xpl=linspace(xl, xr, 500);% для графика F(x)

ypl=cdf (tdistr{bdistr}, xpl, param (bdistr, 1), param (bdistr, 2));

holdon% для рисования на этом же графике

plot(xpl, ypl, 'r');% дорисовали F(x)

hold off

set (get(gcf, 'CurrentAxes'),…

'FontName', 'Times New Roman Cyr', 'FontSize', 12)

title(['\bfПодобрано ' s{bdistr}])

xlabel ('\itx')% метка оси x

ylabel ('\itf\rm (\itx\rm)')% метка оси y

Результат:

Лучше всего подходит нормальное распределение;

критический уровень значимости для него = 0.31369

Рис. 11 – График эмпирической функции распределения для сигнала гусеничной техники

Рис. 12 – График эмпирической функции распределения для фонового сигнала

Найденный критический уровень значимости – это то значение q , при котором неравенство (19) обращается в равенство.

Вывод: По полученным результатам можно сделать вывод, что по данному критерию распределение подобранно верно.

1.6 Проверка гипотезы по критерию согласия Пирсона

По критерию Пирсона сравниваются теоретическая и эмпирическая функции плотности распределения вероятности, а точнее – частота попадания случайной величины в интервал. Интервалы могут быть любыми, равными и неравными, но удобно использовать те интервалы, на которых построена гистограмма. Эмпирические числа попадания n (из гистограммы) сравнивается с теоретическим np_j , где p_j – вероятность попадания случайной величины X в j -ый интервал:

, (20)

a_j и b_j – границы j -го интервала. Карл Пирсон показал, что, если все np_j ³ 5, то суммарная квадратическая относительная разность между теоретическим и практическим числом попаданий в интервал равна

(21)

имеет приближенно c² распределение Пирсона с k – m степенями свободы, где m – число параметров, оцениваемых по выборке, плюс 1. Так как параметров два, то m = 3. Выражение (21) представляет собой статистику Пирсона.

Теоретическое распределение можно считать подобранным верно, если выполняется условие

. (22)

Построим таблицу результатов, в которую занесем: номера интервалов (1-й столбец), границы интервалов a_j и b_j (2-й и 3-й столбцы), вероятность попадания в интервал p_j (4-й столбец), теоретическое число попаданий и практическое число попаданий np_j (6-й столбец). Границы интервалов и практическое число попаданий взяты из гистограммы, теоретическая вероятность попадания в j-й интервал подсчитывается по выражению (20).

Практическая часть.

clearTabl% очистили таблицу результатов

Tabl(:, 1)=[1:k]';% номера интервалов

Tabl(:, 2)=xm'-delta/2;% левые границы интервалов

Tabl(:, 3)=xm'+delta/2;% правые границы интервалов

Tabl(1,2)=-inf;% теоретическое начало 1-го интервала

Tabl(k, 3)=inf;% теоретический конец последнего интервала

Tabl(:, 4)=nj';% опытные числа попаданий

bor=[Tabl(:, 2); Tabl(end, 3)];% все границы интервалов

pro=cdf (tdistr{bdistr}, bor, param (bdistr, 1), param (bdistr, 2));

Tabl(:, 5)=pro (2:end) – pro (1:end-1);% вероятности попаданиz pj

Tabl(:, 6)=n*Tabl(:, 5);% теоретическоечислопопаданийnpj

disp('Сводная таблица результатов')

fprintf(' jajbj')

fprintf (' njpjnpj\n')

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f\n', Tabl')

Для сигнала гусеничной техники:

Сводная таблица результатов

j aj bj nj pj npj

1 – Inf -0.09544 2 0.00000 0.01837

2 -0.09544 -0.09464 2 0.00000 0.00408

3 -0.09464 -0.09385 0 0.00000 0.00495

4 -0.09385 -0.09306 1 0.00000 0.00599

5 -0.09306 -0.09226 1 0.00000 0.00724

6 -0.09226 -0.09147 0 0.00000 0.00873

7 -0.09147 -0.09067 0 0.00000 0.01052

8 -0.09067 -0.08988 4 0.00000 0.01266

9 -0.08988 -0.08909 0 0.00000 0.01520

10 -0.08909 -0.08829 0 0.00000 0.01824

11 -0.08829 -0.08750 2 0.00000 0.02184

12 -0.08750 -0.08671 2 0.00000 0.02612

13 -0.08671 -0.08591 0 0.00000 0.03118

14 -0.08591 -0.08512 3 0.00000 0.03718

15 -0.08512 -0.08433 1 0.00000 0.04425

Для фонового сигнала:

Сводная таблица результатов

jajbjnjpjnpj

1 – Inf0.01067 1 0.00000 0.00000

2 0.01067 0.01074 0 0.00000 0.00000

3 0.01074 0.01080 0 0.00000 0.00000

4 0.01080 0.01086 0 0.00000 0.00000

5 0.01086 0.01092 0 0.00000 0.00000

6 0.01092 0.01098 0 0.00000 0.00000

7 0.01098 0.01104 0 0.00000 0.00000

8 0.01104 0.01111 0 0.00000 0.00000

9 0.01111 0.01117 0 0.00000 0.00000

10 0.01117 0.01123 0 0.00000 0.00000

11 0.01123 0.01129 0 0.00000 0.00000

12 0.01129 0.01135 0 0.00000 0.00000

13 0.01135 0.01141 0 0.00000 0.00000

14 0.01141 0.01147 0 0.00000 0.00000

15 0.01147 0.01154 0 0.00000 0.00000

Если распределение подобрано, верно, то числа из 4-го и 6-го столбцов не должны сильно отличаться.

Вывод: Для сигнала гусеничной техники числа из 4-го и 6-го столбцов значительно отличаются, значит, распределение подобрано неверно. А для фонового сигнала эти числа практически совпадают.

Проверим выполнение условия np_j ³ 5 и объединим те интервалы, в которыхnp_j < 5. Перестроим таблицу и добавим в нее еще один, 7-й столбец – слагаемое, вычисляемое по выражению (21).

Практическая часть.

qz=0.3;% выбрали уровень значимости

ResTabl=Tabl (1,1:6);% взяли первую строку

for k1=2:k, % берем остальные строки таблицы

if ResTabl (end, 6)<5, % предыдущее npj<5 – будем суммировать

ResTabl (end, 3)=Tabl (k1,3);% новая правая граница интервала

ResTabl (end, 4:6)=ResTabl (end, 4:6)+Tabl (k1,4:6);% суммируем

else% предыдущее npj>=5 – будем дописывать строку

ResTabl=[ResTabl; Tabl (k1,1:6)];% дописываемстроку

end

if ResTabl (end, 6)<5, % последнее npj<5

ResTabl (end – 1,3)=ResTabl (end, 3);% новаяправаяграница

ResTabl (end – 1,4:6)=ResTabl (end – 1,4:6)+ResTabl (end, 4:6);

ResTabl=ResTabl (1:end-1,:);% отбросили последнюю строку

end

kn=size (ResTabl, 1);% число объединенных интервалов

ResTabl(:, 1)=[1:kn]';% новые номера интервалов

ResTabl(:, 7)=(ResTabl(:, 4) – ResTabl(:, 6)).^2./ResTabl(:, 6);

disp ('Сгруппированная сводная таблица результатов')

fprintf (' jajbj')

fprintf (' njpjnpj')

fprintf([' (nj-npj)^2/npj\n'])

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f % 12.5f\n', ResTabl')

hi2=sum (ResTabl(:, 7));% сумма элементов последнего столбца

fprintf(['Статистика Пирсона chi2=%10.5f\n'], hi2)

m=[3,2,3,2];% число ограничений

fprintf ('Задаем уровень значимости q=%5.4f\n', qz)

chi2qz=chi2inv (1-qz, kn-m(bdistr));% квантиль

fprintf(['Квантиль chi2-распределения Пирсона '…

'chi2 (1-q)=%10.5f\n'], chi2qz)

ifhi2<=chi2qz,

disp ('Распределение подобрано верно, т. к. chi2<=chi2 (1-q)')

else

disp ('Распределение подобрано неверно, т. к. chi2>chi2 (1-q)')

end

Для сигнала гусеничной техники:

Сгруппированная сводная таблица результатов

j aj bj nj pj npj (nj-npj)^2/npj

1 – Inf -0.07004 58 0.00009 5.46033 505.53988

2 -0.07004 -0.06607 32 0.00011 6.16617 108.23348

3 -0.06607 -0.06369 17 0.00011 6.35867 17.80845

4 -0.06369 -0.06210 16 0.00010 5.89961 17.29233

5 -0.06210 -0.06051 16 0.00013 7.65444 9.09908

6 -0.06051 -0.05893 16 0.00017 9.87115 3.80530

7 -0.05893 -0.05813 9 0.00010 5.93889 1.57781

8 -0.05813 -0.05734 16 0.00012 6.71391 12.84370

9 -0.05734 -0.05655 12 0.00013 7.57856 2.57953

10 -0.05655 -0.05575 17 0.00015 8.54160 8.37603

11 -0.05575 -0.05496 15 0.00017 9.61240 3.01967

12 -0.05496 -0.05416 17 0.00019 10.80104 3.55773

13 -0.05416 -0.05337 13 0.00021 12.11825 0.06416

14 -0.05337 -0.05258 26 0.00024 13.57548 11.37115

15 -0.05258 -0.05178 20 0.00026 15.18487 1.52688

Статистика Пирсона chi2=2613.15423

Задаем уровень значимости q=0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 182.25040

Распределение подобрано неверно, т. к. chi2>chi2 (1-q)

Вывод: По критерию Пирсона распределение подобрано неверно, т. к. реальное значение статистики χ² _р =2613.15423 намного превышает критическое значение χ² _т, _f =182.25040, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала не подтверждается на уровне значимости 0.05.

Для фонового сигнала:

Сгруппированная сводная таблица результатов

jajbjnjpjnpj(nj-npj)^2/npj

1 – Inf0.01690 11 0.00026 7.51515 1.61596

2 0.01690 0.01702 13 0.00031 8.99732 1.78070

3 0.01702 0.01708 14 0.00026 7.55999 5.48594

4 0.01708 0.01714 15 0.00037 10.63561 1.79095

5 0.01714 0.01720 13 0.00052 14.78664 0.21588

6 0.01720 0.01727 24 0.00071 20.31617 0.66797

7 0.01727 0.01733 33 0.00097 27.58544 1.06279

8 0.01733 0.01739 35 0.00130 37.01551 0.10975

9 0.01739 0.01745 54 0.00172 49.08550 0.49205

10 0.01745 0.01751 58 0.00225 64.32627 0.62217

11 0.01751 0.01757 79 0.00291 83.30848 0.22282

12 0.01757 0.01764 102 0.00373 106.62418 0.20055

13 0.01764 0.01770 137 0.00472 134.86147 0.03391

14 0.01770 0.01776 167 0.00590 168.57212 0.01466

15 0.01776 0.01782 185 0.00729 208.23287 2.59213

Статистика Пирсона chi2= 57.37478

Задаем уровень значимости q=0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 66.27446

Распределение подобрано, верно, т. к. chi2<=chi2 (1-q)

Вывод: Для фонового сигнала по критерию Пирсона распределение подобрано верно, т. к. реальное значение статистики χ² _р =609411.53699 не превышает критическое значение χ² _т, _f =520.15366, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала подтверждается.

1.7 Построение корреляционной функции для фрагмента сигнала длительностью 2000 отсчетов

Для построения корреляционной функции двух сигналов, выберем фрагменты сигналов:

Практическая часть

%Начало фрагмента задается величиной N1

N1=25001;

% конец фрагмента задается величиной N2

N2=26000;

x=tr_t200 (N1:N2); %вырезали фрагмент сигнала

r=xcorr(x, x); %Вычисление корреляционной функции

Рисунок 13 – График исходного сигнала гусеничной техники

Для сигнала гусеничной техники выбираем наиболее информативный участок от 54000 до 55000.

Рисунок 14 – График исходного фонового сигнала

Для фонового сигнала выбираем наиболее информативный участок то 45000 до 46000.

Для сигнала гусеничной техники:

h1=tr_t200 (54000:55000);% вырезали фрагмент

k=1000;

KF=xcorr (h1, h1, k);% КФ

k1=-k:k; plot (k1, KF);%построили КФ

Рисунок 15 – График корреляционной функции сигнала гусеничной техники

Вывод: График имеет квазипериодический характер. Повтор явных всплесков колебаний через каждые 250÷300 отсчетов. По корреляционной функции также можно сказать, что сигнал имеет колебательный случайный характер. Так же можно сказать, что функция не стационарна, так как дисперсия ее не постоянна. Период колебания корреляционной функции сигнала гусеничной техники составляет примерно 290 отсчетов (0.58 с).

Для фонового сигнала:

h2=fon(15000:16000);% вырезали фрагмент

k=1000;

KF=xcorr (h2, h2, k);% КФ

k1=-k:k; plot (k1, KF);%построили КФ

Рисунок 16 – График корреляционной функции фонового сигнала

Вывод: по корреляционной функции для фонового сигнала можно сказать, что сигнал имеет колебательный случайный характер. Так же можно сказать, что функция не стационарна, так как дисперсия ее не постоянна. Период колебания корреляционной функции фонового сигнала составляет приблизительно 190 отсчетов.

2. Формирование обучающих и контрольных множеств данных

2.1 Признаки по оценке спектра мощности сигнала в восьми интервалах частот

Теоретический раздел

При обнаружении и распознавании объектов по сейсмическим сигналам возникает задача выбора признаков.

Признаки должны удовлетворять двум основным требованиям:

1 Устойчивость. Наиболее устойчивыми считаются признаки, отвечающие нормальному закону распределения (желательно, чтобы значения признаков не выходили за пределы поля допуска);

2 Сепарабельность. Чем больше расстояние между центрами классов и меньше дисперсия в классе, тем выше показатели качества системы обнаружения или классификации.

В данной работе признаками являются: распределение мощности в десяти равномерных интервалах (по 25 гармоник).

Практическая часть

x1=tr_t200-mean (tr_t200);%Введение центрированного сигнала одного

человека.

x2=fon-mean(fon);%Введение центрированного сигнала

группы людей.

Признаки вычисляются с использованием подгружаемого файла MATRPRIZP:

function [P, Ps]=f (x, fs, N1, N2)

% Программа вычисления матрицы признаков относительной мощности

% сигнала в 10-ти поддиапазонах частот

% Обращение к процедуре: P=MATRPRIZP(x, fs, N1, N2); или [P, Ps]=MATRPRIZP(x, fs, N1, N2);

% x– исходный дискретный сигнал

% P– матрица признаков

% Ps– матрица сглаженных признаков

% Pk – спектр мощность сигнала в текущем окне

% N1 – длинна нарезанных сигналов в отсчетах

% N2 – сдвиг в отсчетах между соседними сигналами

% M– матрица сигналов размерности N1*N2

% Nc– число строк матрицы сигналов

M=matrsig (x, N1, N2);

Nc=length (M(:, 1));

for i=1: Nc Pk(:, i)=SM (M(i,:)', N1, fs); end;

Pk=Pk';

for i=1: Nc

w=sum (Pk(i,:));

P (i, 1)=sum (Pk(i, 1:51))/w; P (i, 2)=sum (Pk(i, 52:103))/w; P (i, 3)=sum (Pk(i, 104:155))/w; P (i, 4)=sum (Pk(i, 156:207))/w;…

P (i, 5)=sum (Pk(i, 208:259))/w; P (i, 6)=sum (Pk(i, 260:311))/w; P (i, 7)=sum (Pk(i, 312:363))/w; P (i, 8)=sum (Pk(i, 364:415))/w; P (i, 9)=sum (Pk(i, 416:467))/w; P (i, 10)=sum (Pk(i, 468:512))/w;

end;

Пропускаем сигналы через формирование матрицы признаков:

x=tr_t200;

N1=1024;

N2=512;

fs=500;

Mt=MATRPRIZP (x, fs, N1, N2);

x=fon;

N1=1024;

N2=512;

fs=500;

Mf=MATRPRIZP (x, fs, N1, N2);

Получим графические представления матриц признаков:

Рисунок 17 – Графическое представление матрицы признаков сигнала гусеничной техники

Рисунок18 – Графическое представление матрицы признаков фонового сигнала

3 Исследование признаков

Практическая часть

Для обучающей матрицы произвести исследование признаков по следующей программе: 1) Оценить параметры распределения признаков; 2) По каждому признаку обучающей матрицы вычислить расстояние. Для данного признака сформулировать решающее правило задачи обнаружения.

Загружаем сигнал в рабочее пространство:

h1=fon-mean(fon);

h2=tr_t200-mean (tr_t200);

N1=1024;

N2=512;

fs=500;

Пропускаем сигнал через решетку фильтров Батерворда:

[M, Mf]=MATRPRIZP (h1,500, N1, N2);

[M, Mt]=MATRPRIZP (h2,500, N1, N2);

Находим математическое ожидание и дисперсию для 2-х сигналов:

VMf=mean(Mf);

VMf =

0.7424 0.0651 0.0439 0.0353 0.0353 0.0289 0.0200 0.0135 0.0093 0.0054

VMs=mean(Mt);

VMs =

0.9563 0.0424 0.0006 0.0002 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001

VSf=std(Mf);

VSf =

0.0676 0.0144 0.0119 0.0103 0.0131 0.0107 0.0056 0.0030 0.0018 0.0016

VSs=std(Mt);

VSs =

0.0234 0.0232 0.0003 0.0001 0.0001 0.0001 0.0001 0.0000 0.0000 0.0000

npr=10;

for i=1:npr

r(i)=abs (VMf(i) – VMs(i))/(VSf(i)+VSs(i));

end;

[max_r, ind]=max(r);

Расстояние между признаками r=

2.3638 0.67807 3.5322 3.2243 2.3307 2.9455 4.0058 4.756 4.3383 3.2031

Максимальное расстояние: max_r= 4.756;

Получили наиболее информативный признак под номером 8. Следовательно, нормированное значение мощности в диапазоне 364 – 415 Гц.

ind=8;

x1=Mt(:, ind);

x1=sort(x1);

n1=length(x1);

xmin1=x1 (1);

xmax1=x1 (n1);

Mx1=mean(x1);

Sx1=std(x1);

xl1=Mx1–3*Sx1;

xr1=Mx1+3*Sx1;

xft1=linspace (xl1, xr1,1000);

ft1=[normpdf (xft1, Mx1, Sx1)];

k1=round (n1^0.5);

d1=(xmax1-xmin1)/k1;

x2=Mf(:, ind);

x2=sort(x2);

n2=length(x2);

xmin2=x2 (1);

xmax2=x2 (n2);

Mx2=mean(x2);

Sx2=std(x2);

xl2=Mx2–3*Sx2;

xr2=Mx2+3*Sx2;

xft2=linspace (xl2, xr2,1000);

ft2=[normpdf (xft2, Mx2, Sx2)];

k2=round (n2^0.5);

d2=(xmax2-xmin2)/k2;

plot (xft1, ft1.*d1,'b', xft2, ft2.*d2,'r');

chi=(2*Sx1*Sx2*log (Sx2/Sx1))+Mx1^2-Mx2^2;

Zn=2*(Mx1-Mx2);

h=chi/Zn

Получили порог принятия решения:

h = 0.0063

Построим график плотности распределения вероятности:

Рисунок 19 – Совмещенные графики плотностей распределения вероятностей сигналов гусеничной техники и фона

Решающее правило: если значения признака будет меньше порога h, то принимаем решение, что это полезный сигнал, если же значения признака больше порога h это будет соответствовать отсутствию сигнала (фону).

Вывод: в данной части курсовой работы были получены матрицы признаков сигнала гусеничной техники и фонового сигналов. Были найдены значение и номер наиболее информативного признака. Но по этому признаку нельзя построить систему классификации, т. к. будет слишком велика ошибка. Поэтому систему классификации целесообразно строить по нескольким признакам.

Также было получено значение порога принятия решения для системы классификации и сформулировано решающее правило.

4. Обучение нейронной сети.

4.1 Общие сведения о нейронных сетях

Искусственные НС представляет собой модели, в основе которых лежат современные представления о строении мозга человека и происходящих в нем процессах обработки информации. ИНС уже нашли широкое применение в задачах: сжатия информации, оптимизации, распознавание образов, построение экспертных систем, обработки сигналов и изображений и т.д.

Связь между биологическим и искусственным нейронами

Рисунок 20 – Структура биологического нейрона

Нервная система человека состоит из огромного количества связанных между собой нейронов, порядка 10¹¹ ; количество связей исчисляется числом 10¹⁵ .

Представим схематично пару биологических нейронов (рисунок 20).Нейрон имеет несколько входных отростков – дендриты, и один выходной – аксон. Дендриты принимают информацию от других нейронов, аксон – передает. Область соединения аксона с дендритом (область контакта) называется синапсом. Сигналы, принятые синапсами, подводятся к телу нейрона, где они суммируются. При этом, одна часть входных сигналов являются возбуждающими, а другая – тормозящими.

Когда входное воздействие превысит некоторый порог, нейрон переходит в активное состояние и посылает по аксону сигнал другим нейронам.

Искусственный нейрон – это математическая модель биологического нейрона (Рисунок 21). Обозначим входной сигнал через х , а множество входных сигналов через вектор X = {х 1, х 2, …, х N }. Выходной сигнал нейрона будем обозначать через y .

Изобразим функциональную схему нейрона.

Рисунок 21 – Искусственный нейрон

Для обозначения возбуждающего или тормозящего воздействия входа, введем коэффициенты w ₁ , w ₁ , …, w_N – на каждый вход, то есть вектор

W = {w ₁ , w ₁ , …, w_N }, w ₀ – величина порога. Взвешенные на векторе W входные воздействия Х перемножаются с соответствующим коэффициентом w , суммируются и формируется сигнал g :

Выходной сигнал является некоторой функцией от g

где F – функция активации. Она может быть различного вида:

1) ступенчатой пороговой

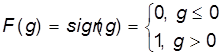
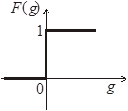или

В общем случае:

2) линейной, которая равносильна отсутствию порогового элемента вообще

F (g ) = g

3) кусочно-линейной, получаемая из линейной путем ограничения диапазона её изменения в пределах , то есть

4) сигмоидальной

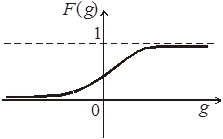
5) многопороговой

6) гиперболический тангенс

F (g ) = tanh(g )

Чаще всего входные значения преобразуются к диапазону X Î [0, 1]. При w_i = 1 (i = 1, 2,…, N ) нейрон является мажоритарным элементом. Порог в этом случае принимает значение w ₀ = N /2.

Еще один вариант условного изображения искусственного нейрона приведен на рисунке 22

Рисунок 22 – Условное обозначение искусственного нейрона

С геометрической точки зрения, нейрон при линейной функции активации описывает уравнение линии, если на входе одно значение x ₁

или плоскости, когда на входе вектор значений Х

Структура (архитектура, топология) нейронных сетей

Существует множество способов организации ИНС, в зависимости от: числа слоев, формы и направления связей.

Изобразим пример организации нейронных сетей (рисунок 23).

Однослойная структура Двухслойная структура с обратными связями с обратными связями

Двухслойная структура Трехслойная структура с прямыми связями с прямыми связями

Рисунок 23 – Примеры структур нейронных сетей

На рисунке 24 изображена трехслойная НС с прямыми связями. Слой нейронов, непосредственно принимающий информацию из внешней среды, называется входным слоем, а слой, передающий информацию во внешнюю среду – выходным. Любой слой, лежащий между ними и не имеющий контакта с внешней средой, называется промежуточным (скрытным) слоем. Слоев может быть и больше. В многослойных сетях, как правило, нейроны одного слоя имеют функцию активации одного типа.

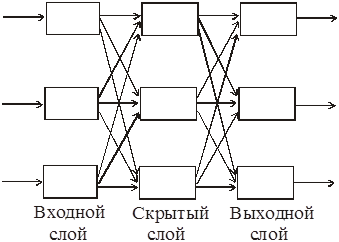
Рисунок 24 – Трехслойная нейронная сеть

При конструировании сети в качестве исходных данных выступают:

– размерность вектора входного сигнала, то есть количество входов;

– размерность вектора выходного сигнала. Число нейронов в выходном слое, как правило, равно числу классов;

– формулировка решаемой задачи;

– точность решения задачи.

Например, при решении задачи обнаружения полезного сигнала НС может иметь один или два выхода.

Создание или синтез НС – это задача, которая в настоящее время теоретически не решена. Она носит частный характер.

Обучение нейронных сетей

Одним из самых замечательных свойств нейронных сетей является их способность обучаться. Несмотря на то, что процесс обучения НС отличается от обучения человека в привычном нам смысле, в конце такого обучения достигаются похожие результаты. Цель обучения НС заключается в её настройке на заданное поведение.

Наиболее распространенным подходом в обучении нейронных сетей является коннекционизм. Он предусматривает обучение сети путем настройки значений весовых коэффициентов wij , соответствующих различным связям между нейронами. Матрица W весовых коэффициентов wij сети называется синаптической картой. Здесь индекс i – это порядковый номер нейрона, из которого исходит связь, то есть предыдущего слоя, а j – номер нейрона последующего слоя.

Существует два вида обучения НС: обучение с учителем и обучение без учителя.

Обучение с учителем заключается в предъявлении сети последовательности обучаемых пар (примеров) (Х i , Hi ), i = 1, 2, …, m образов, которая называется обучающей последовательностью. При этом для каждого входного образа Х i вычисляется реакция сети Y_i и сравнивается с соответствующим целевым образом H_i . Полученное рассогласование используется алгоритмом обучения для корректировки синаптической карты таким образом, чтобы уменьшить ошибку рассогласования. Такая адаптация производится путем циклического предъявления обучающей выборки до тех пор, пока ошибка рассогласования не достигнет достаточно низкого уровня.

Хотя процесс обучения с учителем понятен и широко используется во многих приложениях нейронных сетей, он всё же не полностью соответствует реальным процессам, происходящим в мозге человека в процессе обучения. При обучении наш мозг не использует какие-либо образы, а сам осуществляет обобщение поступающей извне информации.

В случае обучения без учителя обучающая последовательность состоит лишь из входных образов Х i . Алгоритм обучения настраивает веса так, чтобы близким входным векторам соответствовали одинаковые выходные векторы, то есть фактически осуществляет разбиение пространства входных образов на классы. При этом до обучения невозможно предсказать, какие именно выходные образы будут соответствовать классам входных образов. Установить такое соответствие и дать ему интерпретацию можно лишь после обучения.

Обучение НС можно рассматривать как непрерывный или как дискретный процесс. В соответствии с этим алгоритмы обучения могут быть описаны либо дифференциальными уравнениями, либо конечно-разностными. В первом случае НС реализуется на аналоговой, во втором – на цифровых элементах. Мы будем говорить только о конечно-разностных алгоритмах.

Фактически НС представляет собой специализированный параллельный процессор или программу, эмулирующую нейронную сеть на последовательной ЭВМ.

Большинство алгоритмов обучения (АО) НС выросло из концепции Хэбба. Он предложил простой алгоритм без учителя, в котором значение веса w_ij , соответствующее связи между i -м и j -м нейронами, возрастает, если оба нейрона находятся в возбужденном состоянии. Другими словами, в процессе обучения происходит коррекция связей между нейронами в соответствии со степенью корреляции их состояний. Это можно выразить в виде следующего конечно-разностного уравнения:

где w_ij ( t + 1) и w_ij ( t ) – значения веса связей нейрона i с нейроном j до настройки (на шаге t +1) и после настройки (на шаге t ) соответственно; v_i (t ) – выход нейрона i и выход нейрона j на шагеt ; v_j (t ) – выход нейрона j на шагеt ; α– параметр скорости обучения.

Стратегия обучения нейронных сетей

Наряду с алгоритмом обучения не менее важным является стратегия обучения сети.

Одним из подходов является последовательное обучение сети на серии примеров (Х _i , H_i ) i = 1, 2, …, m , составляющих обучающую выборку. При этом сеть обучают правильно реагировать сначала на первый образ Х ₁ , затем на второй Х ₂ и т.д. Однако, в данной стратегии возникает опасность утраты сетью ранее приобретенных навыков при обучении каждому следующему примеру, то есть сеть может «забыть» ранее предъявленные примеры. Чтобы этого не происходило, надо сеть обучать сразу всем примерам обучающей выборки.

Х ₁ ={Х ₁₁ ,…, Х ₁ _N } можно обучать 100 ц 1

Х ₂ = {Х ₂₁ ,…, Х ₂ _N } 100 ц 2 100 ц

……………………

Х _m = {Х _m ₁ ,…, Х _mN } 100 ц 3

Так как решение задачи обучения сопряжено с большими сложностями, альтернативой является минимизация целевой функции вида:

где l_i – параметры, определяющие требования к качеству обучения нейронной сети по каждому из примеров, такие, что λ₁ + λ₂ + … + λ_m = 1.

Практическая часть.

Сформируем обучающее множество:

P_o=cat(1, Mt, Mf);

P_o=P_o';

Зададим структуру нейронной сети для задачи обнаружения:

net = newff(minmax(P_o), [npr 2], {'logsig', 'logsig'}, 'trainlm', 'learngdm');

net.trainParam.epochs = 100;% заданное количество циклов обучения

net.trainParam.show = 5;% количество циклов для показа промежуточных результатов;

net.trainParam.min_grad = 0;% целевое значение градиента

net.trainParam.max_fail = 5;% максимально допустимая кратность превышения ошибки проверочной выборки по сравнению с достигнутым минимальным значением;

net.trainParam.searchFcn = 'srchcha';% имя используемого одномерного алгоритма оптимизации

net.trainParam.goal = 0;% целевая ошибка обучения

Функция newff предназначена для создания «классической» многослойной нейронной сети с обучением по методу обратного распространения ошибки. Данная функция содержит несколько аргументов. Первый аргумент функции – это матрица минимальных и максимальных значений обучающего множества Р_о, которая определяется с помощью выражения minmax (P_o).

Вторые аргументы функции, задаются в квадратных скобках и определяют количество и размер слоев. Выражение [npr 2] означает, что нейронная сеть имеет 2 слоя. В первом слое – npr=10 нейронов, а во втором – 2. Количество нейронов в первом слое определяется размерностью входной матрицы признаков. В зависимости от количества признаков в первом слое может быть: 5, 7, 12 нейронов. Размерность второго слоя (выходной слой) определяется решаемой задачей. В задачах обнаружения полезного сигнала на фоне микросейсма, классификации по первому и второму классам, на выходе нейронной сети задается 2 нейрона.

Третьи аргументы функции определяют вид функции активации в каждом слое. Выражение {'logsig', 'logsig'} означает, что в каждом слое используется сигмоидально-логистическая функция активации , область значений которой – (0, 1).

Четвертый аргумент задает вид функции обучения нейронной сети. В примере задана функция обучения, использующая алгоритм оптимизации Левенберга-Марквардта – 'trainlm'.

Первые половина векторов матрицы Т инициализируются значениями {1, 0}, а последующие – {0, 1}.

net=newff (minmax(P_o), [10 2], {'logsig', 'logsig'}, 'trainlm', 'learngdm');

net.trainParam.epochs = 1000;

net.trainParam.show = 5;

net.trainParam.min_grad = 0;

net.trainParam.max_fail = 5;

net.trainParam.searchFcn = 'srchcha';

net.trainParam.goal = 0;

Программа инициализации желаемых выходов нейронной сети Т:

n1=length (Mt(:, 1));

n2=length (Mf(:, 1));

T1=zeros (2, n1);

T2=zeros (2, n2);

T1 (1,:)=1;

T2 (2,:)=1;

T=cat (2, T1, T2);

Обучениенейросети:

net = train (net, P_o, T);

Рисунок 25 – График обучения нейронной сети.

Произведем контроль нейросети:

P_k=[Mt; Mf];

P_k=P_k';

Y_k=sim (net, P_k);

Команда sim передает данные из контрольного множества P_kна вход нейронной сети net, при этом результаты записываются в матрицу выходов Y_k. Количество строк в матрицах P_kи Y_kсовпадает.

Pb=sum (round(Y_k (1,1:100)))/100

Оценка вероятности правильного обнаружения гусеничной техники Pb=1 alpha = sum (round(Y_k (1,110:157)))/110

Оценка вероятности ложной тревоги alpha =0

Определяем среднеквадратическую ошибку контроля с помощью желаемых и реальных выходов нейронной сети Еk.

[Ek] = T-Y_k;

sqe_k = mse(Ek)

Величина среднеквадратической ошибки контроля составляет:

sqe_k = 2.5919e-026

Протестируем работу нейросети. Для этого сформируем матрицу признаков тестового сигнала:

h3=tr_t50-mean (tr_t50);

Mh1=MATRPRIZP (h3,500, N1, N2);

Mh1=Mh1 (1:50,:);

P_t=[Mh1; Mt];

P_t=P_t';

Y_t=sim (net, P_t);

Pb=sum (round(Y_t (1,1:100)))/100

Оценка вероятности правильного обнаружения гусеничной техники Pb=1

Находим разницу желаемых и реальных выходов нейронной сети Е и определяем среднеквадратическую ошибку тестирования.

[Ek] = T-Y_t;

sqe_t = mse(Ek)

Величина среднеквадратической ошибки тестирования составляет:

sqe_t = 3.185e-025

Вывод: в данном разделе мы построили модель обнаружителя сейсмических сигналов на нейронной сети с обучением по методу обратного распространения ошибки. Задача обнаружения решается с не большими погрешностями, следовательно признаки подходят для обнаружения.

Данную двухслойную нейронную сеть можно применить в построении системы обнаружения объектов.

Заключение

Целью данной курсовой работы было изучение методов обработки информации и применение их для решения задач обнаружения объектов.

В ходе проделанной работы, которая выполнялась в четыре этапа, были получены следующие результаты:

1) Были построены гистограммы выборочных плотностей вероятности амплитуд сигналов, как случайных величин.

Оценены параметры распределения: математическое ожидание, дисперсию, среднеквадратическое отклонение.

Сделали предположение о законе распределения амплитуды и проверили гипотезу по критериям Колмогорова-Смирнова и Пирсона на уровне значимости 0,05. По критерию Колмогорова-Смирнова распределение подобрано, верно. По критерию Пирсона распределение подобрано верно только для фонового сигнала. Для него приняли гипотезу о нормальном распределении.

Приняли сигналы за реализации случайных функций и построили для них корреляционные функции. По корреляционным функциям определили, что сигналы имеют случайный колебательный характер.

2) Сформировали обучающее и контрольное множества данных (для обучения и контроля нейронной сети).

3) Для обучающей матрицы оценили параметры распределения признаков: математическое ожидание, дисперсию, среднее квадратическое отклонение. По каждому признаку обучающей матрицы заданных классов вычислили расстояние и выбрали признак с максимальной разностью. Вычислили порог принятия решения и построили на одном графике кривые плотности распределения вероятности. Сформулировали решающее правило.

4)Обучили двухслойную нейронную сеть на решение задачи классификации. Оценили вероятности правильного обнаружения и ложной тревоги. Те же показатели оценили по тестовым сигналам.

Список используемой литературы

1. Лекции по теории обработки информации в СБЛ. Лектор: Чистова Г.К.

2. Чистова Г.К. «Основы обработки и обнаружения случайных сигналов»

3. Вентцель Е.С. «Теория вероятности и математическая статистика»