| Скачать .docx |
Реферат: Анализ медико-биологических данных с помощью Microsoft Excel и СПП STADIA 6.2
Анализ медико-биологических данных с помощью Microsoft Excel и СПП STADIA 6.2
Реферат выполнила аспирант кафедры биохимии и биотехнологии Ли Ирина Арсентьевна
Министерство образования Российской Федерации
Дальневосточный государственный университет
2002
В развитых странах практически любое решение: политическое, финансовое, техническое, научно-исследовательское и даже бытовое решение принимается только после всестороннего анализа данных. Поэтому изучение прикладной статистики и методов анализа данных является неотъемлемым компонентом образования на всех уровнях, а компьютерные пакеты для аналитических исследований и прогнозирования являются настольным рабочим инструментом любого специалиста, так или иначе связанного с информационной сферой.
Известно, что окружающий нас мир характеризуется постоянной изменчивостью, порождающей разнообразие возможностей и свободу выбора. Однако тот, кто серьезно думает о перспективах своей деятельности, обязательно будет накапливать информацию об окружающем мире, пытаясь выделить закономерности из случайностей.
Именно таким мощным и гибким инструментом отсеивания закономерностей от случайностей и является аппарат математической статистики.
Для современной науки характерно применение точных математических методов в самых различных областях. Точность и уровень той или иной области человеческих знаний часто определяется степенью использования соответствующим разделом науки математических методов.
Эволюционная теория Ч. Дарвина, явилась по существу первой эволюционной теорией, которая привнесла в исследования вероятностный дух. Анализ взаимозависимости между такими исходными понятиями эволюционной теории, как изменчивость, наследственность и отбор, оказался бы несостоятельным без того, что сейчас называется вероятностным стилем мышления. Сегодня исследование проблем организации, функционирования, взаимодействия и эволюции живых систем уже немыслимо без привлечения идей и методов теории вероятностей, математической статистики и других разделов математики .
Характерной особенностью математизации биологии в наши дни является стремительный рост спроса на такие методы эмпирического материала, которые обеспечивают комплексный подход к познанию живых организмов. В исследовательской работе не всегда учитывается принцип единства и взаимосвязанности явлений в природе. Ярче всего это проявляется при организации наблюдений и экспериментов по принципу единственного фактора, которому многое жертвовалось: вводились различные ограничения и оправдывались существенные упрощения, разрабатывались искусственный схемы исследований и т.д. В результате допускалась методологическая ошибка: игнорировался принцип единства живой природы. Известно, что упущения методологического характера нельзя исправить никакими методами, в том числе и математическими. Принцип единственного фактора вошел в биологию по объективным причинам, среди которых первостепенное значение имеет факт, что человек не может непосредственно анализировать одновременное взаимодействие многих факторов.
Такие математические методы, которые разработаны с всесторонним учетом принципа единства живой природы и возможности практической их реализации с использование программного обеспечения, является достижением в области постановки и анализа биологических исследований. Однако, опыт показывает, что и в век вычислительной техники лучших успехов достигают те специалисты, которые умеют не только использовать обработанную информацию, но также уяснили сущность применяемых методов. Это предохранит от механического их использования, которое рано или поздно приводит к нелепым или даже абсурдным выводам.
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Математическая статистика исходит из предположения, что наблюдаемая изменчивость наблюдаемого мира имеет два источника. Один из них действие известных причин и факторов. Они порождают изменчивость, закономерно объяснимую. Именно эти изменения и вызывающие ее факторы обычно представляют интерес у исследователя, ищущего, в первую очередь, причинные связи явлений.
Однако большинство природных и общественных явлений обнаруживают изменчивость, которая не может быть целиком объяснена закономерными причинами. В таком случае прибегают к концепции случайной изменчивости, которая в данном контексте означает «подчиняющийся законам вероятности». И если предположение о таком характере явлений справедливо, то оно позволяет делать надежные выводы (достоверность которых контролируется) из данных, которые зачастую противоречивы, искажены ошибками, ненадежны и т.д. Без привлечения статистических понятий в таких случаях невозможно судить о точности и обоснованности выводов, но и вообще об их адекватности.
Практика накопила большой опыт того, в каких ситуациях приемлемы представления о случайной изменчивости. Для наиболее ходовых из таких ситуаций разработаны математические модели. Наиболее важные и употребительные модели отражены в компьютерных статистических пакетах. Программное воплощение теоретических схем бывает весьма разнообразным, равно как и возможности и производительность реализуемых алгоритмов, а также удобство использования и работы с пакетом.
Кроме основного ядра, в той или иной форме представленного в большинстве пакетов общего назначения, многие из них уделяют предпочтительное внимание отдельным разделам математической статистики и могут содержать менее традиционный или даже новый, оригинальный материал по этим разделам.
Даже в самых конкретных биологических исследованиях основной интерес представляют сведения, относящиеся не к индивидуальному объекту, а к целой группе или некоторому статистическому среднему объекту. Необходимость использования статистических методов в биологических и медицинских исследованиях связана в первую очередь с тем, что свойства биологических объектов обычно значительно варьируют в пределах популяции, а физиологические и другие параметры одной особи испытывают флуктуации во времени.
Традиционно тесные связи между биологической проблематикой и собственно математической статистикой, уже давно позволили выделить рассматриваемую область прикладной статистики в отдельную дисциплину – биометрию.
Биометрия – область научных знаний, охватывающая планирование и анализ результатов количественных биологических экспериментов и наблюдений методами математической статистики.
Современный количественный эксперимент включает в себя самостоятельное математико-статистической исследование, которое начинается со статистического планирования эксперимента, то есть организации его постановки, и завершается статистической обработкой полученных результатов. Поэтому биометрия находит себе все более широкое общебиологическое применение, ибо задачи, которые она решает – планирование экспериментов и анализ их результатов, - составляют основу экспериментальной работы в любой частной области биологии.
Биометрия строится на строгом математическом фундаменте, но этим не ограничивается.
Построение биометрии идет по четырем основным разделам:
Отбор из громадного арсенала математических методов таких, который могут помочь биологам в их текущей работе по наблюдению, преобразованию живой природы;
Модификация отобранных математических методов в соответствии со специфическими особенностями биологических объектов и процессов
Разработка новых биометрических методов, требуемых современным развитием биологии, но еще не имеющихся в арсенале общей математики. Например, расчет показателей наследуемости и повторяемости;
Унификация терминологии и символики. В общей математике нет единой системы терминов и символики, имеется большое разнообразие в названиях и обозначениях по каждому показателю. При создании биометрической терминологии большинство терминов заимствуется. Но не всегда математические термины пригодны в биологии. Например, такое биологическое явление, как неодинаковость объектов в группе, неизбежное их различие в математике обозначается многими терминами, совершенно не соответствующими сущности этого явления: «изменчивость», «рассеяние», «колеблемость», «разброс». Поэтому в биометрии все они заменены одним общим термином «разнообразие».
Опираясь на такие особенности ЭВМ, как быстродействие, способность хранить большие объемы информации, предоставление по использованию прикладных программ, существование разнообразных форм выдачи результатов вычислений, расширились возможности биометрии, она стала более доступной. Биометрия основывается теперь не только на таких математических дисциплинах, как теория вероятностей и математическая статистика, но на информатике и программировании на ЭВМ. Это позволяет говорить о современной биометрии как о компьютерной.
Стандартные статистические методы включены в состав популярных электронных таблиц, таких как Excel, Lotus 1-2-3, QuattroPro, а также в математические пакеты общего назначения, например Mathcad, Maple и др. Однако гораздо большими возможностями обладает специализированное программное обеспечение – статистические программные продукты (СПП).
Международный рынок насчитывает более 1000 пакетов, решающих задачи статистического анализа данных в среде операционных систем Windows, DOS, OS/2.
СПП можно разделить на:
Универсальные пакеты – предлагают широкий диапазон статистических методов. В них отсутствует ориентация на конкретную предметную область. Из зарубежных универсальных пакетов наиболее распространены BAS, SPSS, Systat, Minilab, Statgraphics, STATISTICA.
Специализированные пакеты, как правило, реализуют несколько статистических методов или методы, применяемые в конкретной предметной области. Чаще всего это системы, ориентированные на анализ временных рядов, корреляционно-регресионный, факторный или кластерный анализ. Из российских пакетов известны STADIA, Олимп, Класс-Мастер, КВАЗАР, Статистик-Консультант; американские пакеты – ODA, WinSTAT, Statit и т.д.
Современные СПП реализуют ряд системных функций: ассистирование пользователю при выборе способа обработки, автоматическую организацию процесса обработки данных, обеспечение диалогового режима работы пользователя с пакетом, ведение пользовательских баз данных, автоматическое составление отчета о проделанной пользователем работе, совместимость с другими программами и некоторые другие.
Методориентированные СПП, как правило, имеют следующую структуру:
Блок описательной статистики и разведочного анализа исходных данных: анализ резко выделяющихся значение исследуемого признака, восстановление пропущенных значений, частотная обработка исходных данных (построение гистограмм, полигонов частот, вычисление выборочных средних дисперсий и т.д.), проверка статистических гипотез об однородности исследуемых совокупностей, оценка критериев согласия, визуализация распределения статистических данных и др.;
Блок статистического исследования динамики и зависимостей: дисперсионный и ковариационный анализ, корреляционно-регрессионый анализ, анализ временных рядов и др.;
Блок классификации и снижения размерности: дискриминантный анализ, статистических анализ смесей распределений, кластерный анализ и др.;
Блок методов статистического анализа нечисловых данных и экспертых оценок: анализ таблиц сопряженности, логлинейные модели, ранговые методы и др.;
Блок планирования эксперимента и выборочных исследований;
Блок вспомогательных программ.
Следует отметить, что продвижение западных продуктов в российской аудитории наталкивается на ряд ограничений в связи с неадекватностью культурно-исторической ситуации. Эти пакеты предполагают наличие широкого первоначального статистического образования, доступной литературы и консультационных служб. Поэтому они содержат мало экранных подсказок и требуют внимательного изучения документации на английском языке.
Указанных недостатков в значительной степени лишены известные отечественные статистические пакеты: Эвриста, Статистик-Консультант, STADIA, которые устойчиво представлены на рынке в течение последних лет.
Используемая в данной работе СПП STADIA является универсальной системой, покрывающей в той или иной степени большинство основных разделов прикладной статистики, деловой и научной графики, и по своим интегральным возможностям сравнима с популярными зарубежными пакетами. Набор методов математической статистики, представленный в пакете STADIA составлен исходя из следующих соображений:
в пакет входят все наиболее часто применяемые в России и за рубежом статистические методы;
значительная часть их изучается в вузовских курсах и описана в стандартных учебниках;
пакет не перегружен очень новыми и/или сложными узкоспециализированными методами.
В состав Microsoft Excel входит набор средств анализа данных (называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Microsoft Excel относится к весьма популярным и распространенным электронным таблицам, работающий в среде Windows.
В процессе анализа данных, как правило, присутствуют следующие основные этапы:
Ввод данных
Введенные данные обычно отражаются в форме электронной таблицы или матрицы данных, где столбцы представляют различные переменные (например, рост, вес), а строки – измерение значений этих переменных, произведенные в различных условиях, в различное время, у различных объектов и т.п.
Преобразование данных
Данные в электронной таблице можно просмотреть и скорректировать методами ручного редактирования или же полуавтоматического преобразования к виду, адекватному выбранному методу анализа. Здесь может быть использован широкий набор алгебраических, матричных, структурных преобразований, а также комбинирование этих операций в требуемой последовательности. Нередко также требуются удаление из введенных данных высокоамплитудных выбросов (которые могут быть результатом некорректных измерений) и замена или удаление пропущенных (неизмеренных) значений.
Визуализация данных
На данные обязательно следует просто посмотреть, чтобы составить общее (в том числе и интуитивное) представление о характере их изменения, специфических особенностях и закономерностях, что очень важно при выборе стратегии и тактики дальнейшего анализа. Для этого можно использовать как исходное числовое представление, так и различные формы графического изображения.
Статистический анализ
Собственно выбор метода, анализ данных и интерпретация результатов.
Представление результатов
Для наглядности производимых выводов полученные результаты желательно представлять в виде адекватных, убедительных и эффектных графиков.
Комплексное статистическое исследование
Ранее было показано высокое терапевтическое противоопухолевое действие природного соединения – тиакарпина. На первом этапе изучения нового биологически активного вещества исследовали его общее, физиологическое воздействие на организм. Цель данной работы состояла в изучении и поиске наиболее безвредных доз терапевтического препарата.
В связи с этим были получены результаты эксперимента на животных по влиянию тиакарпина на медико-биологические показатели интактного (здорового) организма. В частности регистрировали такие параметры сердечно-сосудистой системы, как активность ферментов аланинаминотрансферазы (АЛТ) и аспарататаминотрансферазы (АСТ), уровень белка, количество лейкоцитов – клеток иммунного реагирования организма. В печени наблюдали состояние белоксинтетической системы по содержанию в ней общего белка и уровень продуктов тиобарбитуровой кислоты (ТБК) – конечных продуктов перекисного окисления липидов.
Животные (в данном случае беспородные лабораторные мыши) были поделены на группы для выяснения дозо-временного действия препарата. Тиакарпин вводили внутрибрюшинно каждый день в течение всего эксперимента за исключением контрольных животных.
Медико-биологическое действие тиакарпина на интактный организм мышей
Таблица 1. Действие различных доз тиакарпина
(7.3 мг/кг, 15мг/кг и 50 мг/кг) на третьи и шестые сутки
| группа | белок печени | белок сыворотки | АЛТ | АСТ | ТБК |
| мг/100мг | г% | ммоль/л*ч | ммоль/л*ч | мкг/100мг | |
| контроль1 | 85,6 | 7,5 | 1,95 | 5,4 | 0,58 |
| контроль2 | 63,6 | 8,1 | 3,48 | 7,11 | 0,42 |
| 7,5-3 | 66,6 | 3,2 | 3,12 | 5,87 | 0,38 |
| 15-3 | 33,3 | 5,6 | 3,16 | 5,67 | 0,3 |
| 50-3 | 42,4 | 7,8 | 2,64 | 4,41 | 0,2 |
| 7,5-6 | 37,1 | 6,3 | 2,92 | 5,05 | 0,34 |
| 15-6 | 50,7 | 5,1 | 3,77 | 5,49 | 0,4 |
| 50-6 | 59,8 | 5,1 | 2,36 | 4,78 | 0,3 |

Рис 1.1. Содержание белка в печени
Из рис.1.1 видно, что введение тиакарпина в низких дозах на третьи сутки изменяет состояние белоксинтетической функции печени в пределах физиологической нормы в отличие от больших доз. Однако, если содержание белка практически восстанавливается в дозах 15 и 50 мг/кг, то при низких дозах снижается почти в 2 раза.

Рис. 1.2. Содержание белка в сыворотке крови
Обратная картина получена для белка сыворотки крови (рис. 1.2): резкое понижение в первые три дня при малых дозах и восстановление на шестой день. В то же время большие дозы вызывают стабильное понижение концентрации общего белка до 5 г%.
 |
Рис. 1.3. Активность аланинаминотрансферазы и аспартатаминотрансферазы в сыворотке крови
В случае с уровнем активности ферментов крови наблюдается положительная ситуация для всех исследуемых групп. На рис. 1.3 можно видеть незначительные колебания показателей практически в пределах нормы.
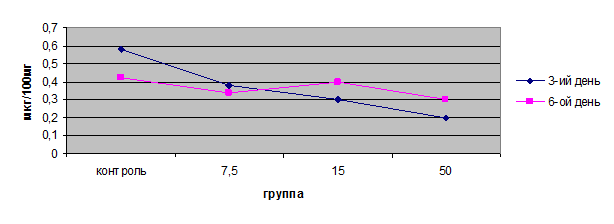
Рис. 1.4. Содержание продуктов тиобарбитуровой кислоты в печени
Содержание ТБК-продуктов выравнивается до нормальных значений во всех группах на шестой день. Наблюдавшееся понижение в первой половине недели находилось в прямой зависимости от дозы.
Анализ результатов на первом этапе не показал негативного действия тиакарпина на показатели организма даже при введении высоких доз, а в некоторых случаях увеличение дозы способствовало подавлению процессов перекисного окисления в печени, свидетельствующее о некотором антиоксидантном и гепатопротекторном действии препарата. Неодназначные результаты были получены по влиянию тиакарпина на белоксинтетическую функцию организма.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Переменная Размер <---Диапазон---> Среднее---Ошибка Дисперс Ст.откл Сумма
x1 8 33,3 85,6 54,89 6,177 305,2 17,47 439,1
x2 8 3,2 8,1 6,087 0,5908 2,793 1,671 48,7
x3 8 1,95 3,77 2,925 0,2099 0,3523 0,5936 23,4
x4 8 4,41 7,11 5,473 0,2888 0,6673 0,8169 43,78
x5 8 0,2 0,58 0,365 0,03942 0,01243 0,1115 2,92
Переменная Медиана <--Квартили--> ДовИнтСр. <-ДовИнтДисп-> Ош.СтОткл
x1 55,25 38,42 65,85 21,61 105,4 2160 8,953
x2 5,95 5,1 7,725 2,067 0,9648 19,76 0,8564
x3 3,02 2,43 3,4 0,7343 0,1217 2,493 0,3042
x4 5,445 4,848 5,82 1,011 0,2305 4,722 0,4186
x5 0,36 0,3 0,415 0,1379 0,004294 0,08795 0,05713
Переменная Асимметр. Значим Эксцесс Значим
x1 0,3909 0,2584 2,203 0,4266
x2 -0,331 0,2915 2,103 0,372
x3 -0,2451 0,3422 2,132 0,3878
x4 0,7996 0,0924 3,209 0,107
x5 0,5615 0,1758 3,091 0,1412
Для всех анализируемых выборок согласно вычисленным уровням значимости (они больше критического значения 0,05) нет оснований отвергать нулевые гипотезы об отличии коэффициентов эксцесса и асимметрии от значений нормального распределения с вероятностью 95%. Таким образом использование параметрических статистических показателей в данном случае будет оправдано и достоверно.
Сравнивая средние по каждому переменному (диагностикуму) с контрольными (нормальными) показателями можно сказать, что в общем тиакарпин подавляет синтез белка, хотя и незначительно, и снижает уровень продуктов перекисного окисления. Сопоставление средних и дисперсий указывает на то, что препарат оказывает значительное влияние на все показатели и особенно на белковое содержание.
Результаты исследования образуют матрицу данных и, чтобы увидеть закономерность и структуру общей картины эксперимента, необходимо применить многомерные методы анализа данных.
КЛАСТЕРНЫЙ АНАЛИЗ
Эвклид+Дальн.сосед
Таблица расстояний
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
( 2) 22,13
( 3) 19,52 5,889
( 4) 52,35 30,44 33,39
( 5) 43,22 21,39 24,68 9,461
( 6) 48,53 26,65 29,67 3,921 5,554
( 7) 35,03 13,35 16,03 17,42 8,869 13,69
( 8) 25,92 5,49 7,185 26,53 17,61 22,74 9,236
К л а с т е р ы:
(список объектов) -> расстояние
(6,4) --> 3,921
(8,2) --> 5,49
(8,3,2) --> 7,185
(7,5) --> 8,869
(7,6,4,5) --> 17,42
(8,1,3,2) --> 25,92
(8,7,6,4,5,1,3,2) --> 52,35
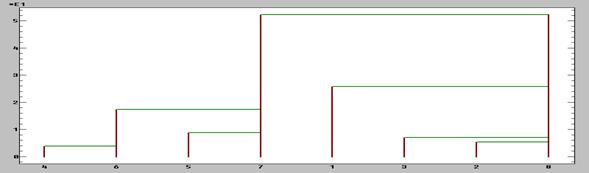 |
Рис. 1.5. Дендрограмма (стратегия дальнего соседа): по оси Y – расстояние объединения, по оси Х – номера групп
Как видно из рис. 1.5. стратегия дальнего соседа достаточно отчетливо выделяет три кластера исследуемых групп: (4, 6), (5, 7) и (1, 2, 3, 8). При этом группу 1 можно выделить в четвертый кластер. В связи с этим применим дивизивную стратегию в попытке получить группировку на четыре кластера.
Эвклид+Дивизивная
Таблица расстояний
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
( 2) 22,13
( 3) 19,52 5,889
( 4) 52,35 30,44 33,39
( 5) 43,22 21,39 24,68 9,461
( 6) 48,53 26,65 29,67 3,921 5,554
( 7) 35,03 13,35 16,03 17,42 8,869 13,69
( 8) 25,92 5,49 7,185 26,53 17,61 22,74 9,236
К л а с т е р ы:
Среднее внутрикластерное расстояние=5,673
1= (1,2,3*,8)
2= (4*,6)
3= (5*,7)

Рис. 1.6. Дендрограмма трех кластеров
В результате получаем разделение на три кластера. Для проверки гипотезы об адекватности получаемых классификаций применяем дискриминантный метод.
ДИСКРИМИНАНТНЫЙ АНАЛИЗ
Расстояние Махаланобиса=724,3, значимость=0
Класс <--- Коэффициенты дискриминантной функции:a[0],a[1],... --->
1 -1181 45,14 58,65 528,6 -206,2 -3207
2 -429,4 26,77 37,61 330,7 -132,4 -1884
3 -1038 42,14 60,77 535,3 -223,7 -2953
Объект Класс D^2 Значим Вероят.отнесения
1 1 3,75 0,5859 1
2 1 3,75 0,5859 1
3 1 3,75 0,5859 1
4 2 2,5 0,7764 1
5 3 2,5 0,7764 1
6 2 2,5 0,7764 1
7 3 2,5 0,7764 1
8 1 3,75 0,5859 1
Как показывают результаты дискриминантного анализа, предполагаемая классификация оказалась эффективной.
Кластеризация исследуемых групп животных выявила сохранение физиологической нормы при введении тиакарпина в течение 3-х дней в дозе 7.5 мг/кг и в течение 6-и дней в дозе 50 мг/кг. Данные дозы оказывают наименьшую нагрузку на организм.
 |
Рис. 1.7. Дендрограмма переменных: по оси Y – расстояние объединения, по оси Х – переменные
Рис. 1.7, иллюстрирующий классификацию переменных – диагностикумов, с использованием метрики на основе коэффициента корреляции и стратегии ближайшего соседа, показывает, что все пять диагностикумов не взаимосвязаны.
Графическая визуализация экспериментальных результатов с помощью Excel показывает, что исследуемое вещество – тиакарпин, не оказывает негативного действия на показатели организма даже при введении высоких доз, а в некоторых случаях увеличение дозы способствовало подавлению процессов перекисного окисления в печени, свидетельствующее о некотором антиоксидантном и гепатопротекторном действии препарата. Неоднозначные результаты были получены по влиянию тиакарпина на белоксинтезирующую функцию организма.
Основываясь на результаты описательной статистики в STADIA 6.2 можно утверждать, что препарат оказывает значительное влияние на все показатели и особенно на белковое содержание. Общее действие тиакарпина направлено на подавление синтеза белка и ингибирование процессов перекисного окисления липидов.
Кластеризация исследуемых групп животных выявила сохранение физиологической нормы при введении тиакарпина в течение 3-х дней в дозе 7.5 мг/кг и в течение 6-и дней в дозе 50 мг/кг. Данные дозы оказывают наименьшую нагрузку на организм.
Использование метрики на основе коэффициента корреляции и стратегии ближайшего соседа показывает, что все пять диагностикумов не взаимосвязаны, т.е. все используемые параметры характеризуют функциональное состояние организма и обладают одинаковой диагностической информативностью.
Список литературы
Елисеева И.И., Юзбашев М.М. Общая теория статистики. Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 1995. – 386 с.
Кулаичев А.П. Методы и средства анализа данных в среде Windows. STADIA 6.0. – М.: Информатика и компьютеры, 1996. – 257 с.
Лукьянова Н.Ю. Статистический анализ данных с использованием компьютера. Учебное пособие. – Калининград: Изд-во КГУ, 2001. – 89 с.
Математический анализ биологических данных / Г.Н. Зайцев, М.: “Наука”, 1991. – 184 с.
Плохинский Н.А. Математические методы в биологии. Учебно-методическое пособие. Изд-во Моск. ун-та, 1978. – 168 с.