Курсовая работа: Курсовая работа: Рішення задач цілочисленного програмування

Курсова робота:

Рішення задач цілочисленного програмування

Зміст

Введення

1. Постановка лінійної цілочисленної задачі

2. Теоретичні основи методів відсікання

3. Перший алгоритм Гомори

4. Другий алгоритм Гомори

5. Алгоритм Дальтона й Ллевелина

6. Алгоритм Данцига

7. Деякі висновки

Висновок

Список літератури

Введення

Серед практично важливих задач відшукання умовного екстремуму лінійної функції важливе місце займають задачі з вимогою цілочисленності всіх (частини) змінних. Вони одержали назву задач цілочисленного програмування.

Історично першою задачею цілочисленного типу є опублікована угорським математиком Е. Егервари в 1932 р. задача про призначення персоналу.

Існують різні методи рішення таких задач, і помітне місце серед них займають методи відсікання. Розглянемо в цій роботі деякі з методів відсікання, попередньо більш докладно розібравшись із постановкою лінійних цілочисленних задач.

1. Постановка лінійної цілочисленної задачі

Серед сукупності п неподільних предметів, кожний i-і (i=1,2,…,п) з яких володіє по i-й характеристиці показником і корисністю знайти такий набір, що дозволяє максимізувати ефективність використання ресурсів величини .

Математична модель цієї задачі може бути представлена в такий спосіб:

в області, певної умовами

(1)

(2)

- цілі, . (3)

знайти рішення при якому максимізується (мінімізується) значення цільової функції

(4)

Якщо ,то (1–4) є моделлю задачі цілочисленного програмування, якщо - моделлю задачі частково цілочисленного програмування.

Часткою случаємо задачі цілочисленного програмування є задача з булевими змінними. Її математична модель у загальному виді записується в такий спосіб:

в області, певної умовами

(5)

(6)

знайти рішення , при якому максимізується (мінімізується) значення функції

(7)

До класу задач цілочисленного програмування примикають задачі, у яких умова цілочисленності всіх або частини змінних замінено вимогою дискретності. А саме, для кожної j-і змінної заздалегідь визначений набір значень (не обов'язково цілих), які вона може приймати: де .

Передбачається, що сільгоспкооперативи, тобто . Математична модель загальної задачі дискретного програмування може бути представлена в такий спосіб:

в області, певної умовами

(8)

(9)

знайти рішення , при якому максимізується (мінімізується) лінійна функція

(10)

Умова (9) визначило назву цього класу; задач. Якщо ,то (8–10) називається задачею дискретного програмування; якщо , те (8–10) називається задачею частково дискретного програмування.

Неважко бачити, що умова (2–3) задачі (1–4) і умова (6) задачі (5–7) є часткою случаємо умови (9) задачі (8–10). Дійсно, (2–3) відповідає тому случаю, коли для . Умова (9) відповідає випадку, коли .

Для задач цілочисленного типу визначене поняття припустимого й оптимального рішення.

Вектор , що задовольняє умовам (1–3) (відповідно (8–9)), називається припустимим рішенням задачі (1–4) (відповідно (8–10)). Припустиме рішення, при якому функція (4) (відповідно (10)) досягає найбільшого (найменшого) значення, називається оптимальним рішенням.

Визначивши поняття припустимого й оптимального рішення, природно порушити питання про їхнє знаходження. Здавалося б, що природний шлях рішення цілочисленної задачі складається в рішенні відповідної лінійної задачі з наступним округленням компонентів її оптимального плану до найближчих цілих чисел. Насправді такий шлях у більшості випадків не тільки веде, від оптимуму, але навіть приводить іноді до неприпустимого рішення задачі.

ПРИКЛАД. В області, певної умовами

– цілі

знайти максимум функції .

Вирішимо задачу геометрично (мал. 1). Область пошуку екстремума – багатокутник ODABC, але тому що лінія рівня цільової функції паралельна стороні АВ багатокутника, екстремум досягається у вершинах і , а також у будь-якій крапці відрізка АВ, і дорівнює 7.

(мал. 1)

Однак нас цікавлять лише крапки із цілочисленними координатами, отже, ні А, ні Вне є припустимим рішенням задачі. Округляючи значення координат А, одержимо Але крапка А' не належить області пошуку. Можна показати, що цілочисленний оптимум досягається в крапках N (3; 2) і M (2; 3) і дорівнює 5. Обидві крапки усередині області пошуку.

Побудований нами приклад показав, що для рішення задач із вимогою цілочисленності необхідно розглянути особливі методи оптимізації; і, крім того, ми бачимо, що оптимальне рішення задач цілочисленного програмування не обов'язково належить границі багатогранника (багатокутника) умов, що було характерно для задач лінійного програмування.

2. Теоретичні основи методів відсікання

Запишемо загальну задачу цілочисленного програмування: в області, певної умовами

(11)

(12)

- цілі, (13)

максимізувати функцію

(14)

Назвемо для кратності задачу (11–14) (£^ц , C) – задачею. Відповідну їй задачу без вимоги цілочисленності змінних, тобто задачу (11, 12, 14) назвемо (£, C) – задачею. Порушимо питання: чи не можна рішення (£^ц , C) – задачі одержати шляхом рішення якоїсь спеціальним образом побудованої задачі без вимоги цілочисленності змінних і такий, що оптимальні рішення вихідної (£^ц , C) – задачі й задачі без вимог цілочисленності змінних будуть збігатися. Іншими словами: чи не можна добре вивчений апарат рішення задач лінійного програмування пристосувати до рішення цілочисленних задач. Принципова відповідь на це питання дає наступна теорема.

Теорема. Нехай £ – багатогранник, £^ц – множина його цілих крапок, R – опукла, лінійна оболонка множини £^ц , тоді:

1) R=R^ц – цілочисленний багатогранник;

2) R^ц = £^ц ;

3) R* – множина опорних рішень задачі (£^ц , C) утримується в багатограннику R^ц .

Доказ. Доведемо, що R – цілочисленний багатогранник. За умовою теореми £ – багатогранник, тому множина його цілих крапок (воно позначено через £^ц) звичайно. Оскільки R - опукла лінійна оболонка цієї кінцевої множини крапок, R - теж багатогранник.

По самому визначенню опуклої лінійної оболонки, вона містить всі опорні плани множини, на яке вона натягнута, тобто багатогранник R містить всі целочисленные крапки £^ц. Тому R – цілочисленний багатогранник. Позначимо його через R^ц . Перша частина теореми доведена.

Доведемо, що R^ц збігається з £^ц. Тому що R – опукла оболонка крапок множини £^ц , те £^ц ÍR^ц .

Покажемо, що справедливо також і протилежна нерівність-включення, т.е. R^ц Í£^ц. Для цього виберемо деякий довільний елемент х°ÎR^ц . Оскільки R^ц містить всі опорні рішення задачі (£^ц , C), те х° задовольняє умовам задачі (£^ц , C), тобто х°Î£^ц. Але оскільки довільний елемент із R^ц належить £^ц , те очевидно, що справедливо R^ц Í£^ц. Зіставляючи протилежні включення R^ц Í£^ц і £^ц ÍR^ц доходимо висновку: що £^ц =R^ц . Друга частина теореми також доведена.

Доказ 3-го пункти теореми є зовсім очевидним. Тому що R^* – множина опорних рішень задачі (£^ц , C), те R^* Í£^ц але £^ц =R^ц , тому R^* ÍR^ц

Теорема доведена.

Наслідком із цієї теореми є той висновок, що оптимальне рішення задачі, областю визначення якої є опукла оболонка, натягнута на область пошуку цілочисленного рішення, збігається з оптимальним рішенням вихідної цілочисленної задачі.

Доведена теорема й наслідок з її показують принципову можливість заміни рішення задачі типу (£^ц , C) деякою процедурою побудови й рішення допоміжної задачі типу (£, C), однак не дають алгоритму рішень. До того ж побудова опуклої оболонки множини £^ц реальних задач – надзвичайно складна, а часом практично нерозв'язна задача,

В 1954 р. Дж. Данциг висловив ідею про те, що побудова опуклої оболонки цілочисленної області для задачі (£^ц , C) можна здійснювати поетапно й вирішувати одержувані при цьому задачі. Однак при цьому виникли питання як будувати обмеження нової задачі і як забезпечити кінцівка процесу.

Відповідь на ці питання був уперше отриманий Р. Гомори, що запропонував алгоритми рішення цілочисленних і. частково цілочисленних задач.

Алгоритм Р. Гомори складається з наступних процедур:

Вирішується (£, C) – задача, що відповідає вихідної (£^ц , C) – задачі.

Отримане оптимальне рішення (£, C) – задачі, якщо воно існує, перевіряється на целочисленність. Якщо умова цілочисленності виконується по всім змінним, то оптимальне рішення (£, C) – задачі є оптимальне рішення (£^ц , C) – задачі. Якщо умова цілочисленності не виконується хоча б по одній координаті, то переходять до третього етапу. Якщо (£, C) – задача, виявляється нерозв'язної, те (£^ц , C) – задача теж рішення не має.

Будується додаткове обмеження, що володіє тим властивістю, що з його допомогою відтинається частина області, у якій утримується оптимальне рішення (£, C) – задачі й не втримується жодного припустимого рішення (£^ц , C) – задачі. Процес побудови додаткових обмежень і рішення одержуваних при цьому (£, C) – задач триває доти, поки не одержимо цілочисленного рішення або не переконаємося в нерозв'язності задачі.

При цьому властивості, який повинне володіти кожне з додаткових обмежень при переході від однієї задачі до іншої наступні:

додаткове обмеження повинне бути лінійним, щоб залишатися в області застосовності апарата лінійного програмування;

додаткове обмеження повинне відтинати частина області, у якій не втримується припустимих рішень цілочисленної (£^ц , C) – задачі, але є знайдене оптимальне рішення нецілочисленної (£, C) – задачі, тобто обмеження повинне мати властивість правильності, що не дозволяє втратити оптимальне рішення вихідної (£^ц , C) – задачі.

Нехай х (£, C) – оптимальне рішення (£, C) – задачі, що є неприпустимим рішенням для (£^ц , C) – задачі. Нерівність

(15)

визначає правильне відсікання, якщо задовольняє

а) умові відсікання: x(?, C) задовольняє нерівності (15)

б) умові правильності: будь-яке припустиме рішення задачі (£^ц , C), задовольняє нерівності (15).

Методи, засновані на використанні процедури побудови правильних відсікань, одержали назву методів відсікання.

3. Перший алгоритм Гомори

Випливаючи загальній схемі методів відсікання, вирішимо (£, C) – задачу (11, 12, 14), що відповідає (£^ц , C) – задачі (11–14). Нехай x(£, C) – її оптимальне рішення. Проаналізуємо координати x(£, C) на цілочисленність. Якщо всі координати вектора x(£, C) цілі, то x(£, C) = x(£^ц , C). Якщо хоча б одна координата, нехай x_i , буде нецілої, надійдемо в такий спосіб.

Позначимо через N сукупність небазисних змінних і на підставі останньої симплексної таблиці запишемо розкладання x_i по небазисним змінним x_i , jÎN

(16)

Тому що x_i – неціла величина, позначимо найближче ціле число, що не перевершує x_i , через [x_i ] і визначимо дробову частину: {x_i }= x_i - [x_i ]. Очевидно, (x_i )>0.

Покажемо, що по i-і рядку симплексної таблиці (?, C) - задачі (у якій коштує неціла координата рішення) можна визначити додаткове лінійне обмеження, що володіє властивостями правильності.

Теорема. Нехай - припустиме рішення (£^ц , C) – задачі, тоді співвідношення

, (17)

, - ціле,

визначають правильне відсікання.

Доказ.

Запишемо вираження (16) у вигляді:

Використовуючи для цього вираження формулу (17), одержимо:

або

На підставі припущень теореми про допустимість рішення

(£^ц , C) – задачі x_i – ціле. Величини [x_io ], - цілі по визначенню, отже, z_i – теж ціле.

Отже, z_i певне формулою (17), ціле. Доведемо що . Доказ будемо вести від противного. Нехай .-

Це значить, що . По визначенню дробової частини . За умовою теореми x – припустиме рішення (£^ц , C) – задачі, тому . Отже,

Тоді повинне виконуватися:

Отже, із припущення заперечності z_i , відразу ж одержуємо тобто z_i – неціле. Оскільки раніше було показано, що z_i , певне формулою (17), є цілим, те тим самим ми прийшли до протиріччя. Отже, припущення, що z_i < 0, невірне. Теорема доведена.

Наслідок. Будь-яке оптимальне рішення x(£, C) (£, C) – задачі, що не є припустимим рішенням (£^ц , C) – задачі, не задовольняє умові правильного відсікання (17).

Доказ. Нехай х (£, C) – оптимальне рішення (£, C) – задачі, x_i0 – дробове.

Покажемо, що х (£, C) не задовольняє умові відсікання. Оскільки план оптимальний, всі небазисні змінні x_i , для jÎN дорівнюють нулю. Тому . З огляду на це, підставимо x_io у формулу (17):

z_i (x (£, C))= – {x_i0 }+0<0 ,

що суперечить умові незаперечності z_i . Наслідок доведений.

Очевидно, що кількість додаткових обмежень буде наростати в міру рішення допоміжних (£, C) – задач, оптимальні плани яких будуть містити нецілі координати, тобто виникає проблема розмірності.

Р. Гомори запропонував прийом, що дозволяє обмежити розміри розглянутих симплексних таблиць допоміжних задач величиною (n+2) (k+1), де n – кількість змінних (£, C) – задачі, k – число небазисних змінних її. Цей прийом ґрунтується на тім, що нас цікавить додаткове обмеження лише як спосіб відсікання нецілочисленного оптимального рішення допоміжної задачі, отриманої на даному кроці, і переходу до наступної задачі.

Послідовність (£, C) – задач позначимо індексом k=0,1,…,відповідному номеру ітерації в послідовному наближенні до рішення вихідної (£^ц , C) – задачі, і позначимо (£_k , C). При цьому (£₀ , C) – задача відповідає (£, C) – задачі (задачі без вимоги цілочисленності).

Змінну z_i , що визначається додатковим лінійним обмеженням (7) і будується по деякої нецілочисленної координаті оптимального рішення (£_k , C) – задачі (k =0, 1, 2,…)позначимо x_n+k+l .

Щоб розмірність послідовності (£_k , C) – задач не зростала, викреслимо із симплекс-таблиці змінну, по якій побудоване додаткове лінійне обмеження.

Після зроблених зауважень перейдемо безпосередньо до викладу обчислювальної схеми.

1. Вирішимо (£_k , C) – задачу (спочатку k = 0) методом послідовного поліпшення плану.

Нехай у базис оптимального рішення ввійшли вектори A_s1 ,…,A_sm ... Параметри останньої симплексної таблиці позначимо через x_ij :

.

Якщо, всі базисні тридцятилітні оптимального рішення x(£_k , C) (£_k , C) – задачі цілі, то x(£_k , C) = x(£^ц , C). Якщо деяка координата x_io оптимального рішення x(£_k , C) неціла, то перейдемо до п. 2.

2. Якщо серед сукупності координат оптимального рішення x(£_k , C) є єдина неціла координата, то додаткове лінійне обмеження (17) будується по цій координаті. Якщо нецілих координат в x(£_k , C) більше однієї, то виберемо координату з найменшим номером. Нехай нею виявилася x_i0 . Складемо додаткове лінійне обмеження

(18)

(19)

3. Додамо умови (18, 19) до умов (£_k , C) – задачі. Одержимо нову (£_{k+1, C) – задачу. Тому що оптимальне рішення x(£k} , C) (£_k , C) – задачі визначало одну з вершин багатогранника умов, то воно може бути обране в якості первісного опорного рішення для знову отриманої задачі. А це означає, що останню симплексну таблицю (£_k , C) – задачі можна взяти в якості вихідної для (£_{k+1, C) – задачі, доповнивши її умовою (18).}

Отже, симплексна таблиця для (£_{k+1, C) – задачі виходить із останньої симплексної таблиці для (£k} , C) – задачі шляхом облямівки (i+1) – й рядком з елементами:

де – небазисні змінні (£_k , C) задачі.

Одержимо нову задачу, змінними якої є . Умови цієї задачі дозволені відносно x_sl ,…,x_sm змінних і нова змінної x_n+k+1 , а лінійна форма виражена через небазисні змінні (£_k , C) – задачі. Тому що ми займаємося максимізацією F(x) і рішення х* для (£_k , C) – задачі оптимально, те всі D_i > 0. Тому процес переходу до нового рішення (£_{k+1, C) – задачі не може бути здійснений по методу уточнення плану. У той же час і тому вектор А0} симплексної таблиці не є опорним рішенням для (£_{k+1, C) – задачі, тому що рішенням називається вектор, всі координати якого ненегативні й задовольняють умові приналежності області £k+l} . Тому назвемо отриманий вектор псевдо рішенням задачі (£_{k+1, C) і перейдемо до подальшого перетворення симплекса-таблиці.}

Позначимо через k номер псевдо рішення (£_k , C) – задачі; тоді напрямним рядком є i+k+ 1-я рядок, k =0, 1, 2,…... Тому на кожному етапі перетворення таблиці вектор A_i+k+i буде виводитися з таблиці. Можна довести, що через кінцеве число кроків або буде знайдене цілочисленне рішення, або буде виявлена її нерозв'язність, а тим самим нерозв'язність (£^ц , C) – задачі.

Якщо рішення (£_k , C) – задачі завершується побудовою оптимального цілочисленного рішення x*, те m , перших його компонентів визначають рішення цілочисленної задачі; якщо серед координат х* є дробові, те один із дробових компонентів (раніше певним правилом) породжує додаткове обмеження й процес рішення повинен бути продовжений з новим рядком, що облямовує. Рядок, використовуваний раніше для облямівки, викреслюється й більше для побудови розширених задач не відновлюється.

Процедуру рішення (£_k , C) – задачі (k=0, 1,…)і аналізу отриманого рішення назвемо великою ітерацією. Номер великої ітерації збігається з номером розв'язуваної (£_k , C) – задачі.

Результатом великої ітерації є перехід до нового (£_{k+1, C) – задачі або закінчення рішення задачі.}

Уведемо: 1) осередок i, у якій будемо запам'ятовувати номер рядка, на підставі якої будується чергове додаткове лінійне обмеження, 2) лічильник r, що відповідає номеру проведеної великої ітерації. Позначимо x*(£^r , C) оптимальне рішення (£^r , C) – задачі. Помітимо, що позначення (£^r , C) – задача, еквівалентне (£_r , C), уведено в блок-схемі для зручності запису.

При деяких умовах вдається довести теорему про кінцівку першого алгоритму Гомори, що ми приведемо без доказу.

Теорема. Нехай множина оптимальних планів задачі (£₀ , C) обмежено й виконуються наступні умови:

1) с_i – цілі коефіцієнти цільової функції F(x) (i =1,2,…,n),рядок цільової функції в симплексній таблиці враховується при виборі рядка для побудови правильного відсікання;

2) справедливо одне із двох тверджень: або цільова функція обмежена знизу на С_o , або задача (£^ц , C) має хоча б один план х'.

Тоді перший алгоритм Гомори вимагає кінцевого числа більших ітерацій.

4. Другий алгоритм Гомори

Другий алгоритм Р. Гомори призначається для рішення задач, у яких вимога цілочисленності накладена на деякі змінні (зокрема й на все). Ми його розглянемо стосовно до задач частково цілочисленного типу, розуміючи, що обчислювальна схема буде справедливої й для задач, повністю цілочисленних.

Нехай в області, певної умовами:

(20)

(21)

– цілі, (22)

потрібно максимізувати функцію

(23)

Метод рішення задачі (20–23) ґрунтується на тій же ідеї, що й метод рішення повністю цілочисленних задач. А саме: будується область £_k , що при k = 0 визначається умовами (20–21); вирішується отримана при цьому задача лінійного програмування (20–21, 23). Якщо задача (20–21, 23) виявляється розв'язної, то отримане оптимальне рішення її аналізується на допустимість для вихідної задачі цілочисленного програмування (20–23). Якщо знайдене рішення виявляється целочисленным, то одночасно воно буде оптимальним для (20–23). Якщо оптимальне рішення (£_k , C) – задачі виявляється неприпустимим для вихідної задачі (20–23), те здійснюється побудова правильного відсікання й перехід до рішення нової задачі,

Другий алгоритм Р. Гомори формулюється у вигляді наступної теореми:

Теорема. Нехай х(£_k , C) – оптимальне рішення (£_k , C) – задачі, – елементи відповідної йому симплексної таблиці. Якщо – неціле , то

(24)

– ціле, (25)

де

(26)

визначає правильне відсікання. Блок-схема другого алгоритму Р. Гомори аналогічна блок-схемі першого алгоритму Р. Гомори й відрізняється лише правилом побудови коефіцієнтів правильного відсікання.

Правило побудови правильного відсікання

Нехай x(£_k , C) не задовольняє умові цілочисленності, – елементи симплексної таблиці, що відповідає отриманому оптимальному рішенню (£_k , C) – задачі. Виберемо i₀ =min {i | i Î (1, 2,…,n),x_i0 ^k –неціле} і будуємо правильне відсікання по формулах (24 – 26).

Умови кінцівки другого алгоритму Гомори:

1) Цільова функція F(x) задовольняє умові цілочисленності. Це враховується при виборі рядка k для побудови правильного відсікання.

2) Виконано принаймні одне із двох умов:

2') цільова функція обмежена знизу на багатогранній множині £= £₀ ;

2») задача (£₀ ^ц , C)має принаймні один план.

За допомогою другого алгоритму Гомори можна (у випадку n₁ =n) вирішувати й повністю цілочисленну задачу лінійного програмування. Однак у цьому випадку немає підстав для порівняння ефективності другого й першого алгоритмів Гомори.

5. Алгоритм Дальтона й Ллевелина

Другий алгоритм Гомори має справа із частково цілочисленними задачами лінійного програмування. Дальтон і Ллевелин розглядають широкий клас задач - частково дискретні задачі лінійного програмування й стосовно до них модифікують другий алгоритм Гомори.

Нагадаємо, що рішенням задачі дискретного програмування будемо називати вектор, координати якого належать £^ц області виду:

(27)

(28)

(29)

і максимізує значення функції

(30)

Будемо припускати, що , тобто і є наперед заданими числами.

Теорема. Нехай x(£_k , C) – оптимальне рішення задачі (27–28, 30), – елементи симплексної таблиці, що відповідає йому.

Якщо x(£_k , C) є неприпустимим рішенням задачі (27–30) і , тоді, використовуючи i-ю рядок симплексної таблиці, можна побудувати відсікання, що володіє властивістю правильності по формулах:

(31)

(32)

де

(33)

Доказ. Перевіримо спочатку умову відсікання. Нехай в оптимальному рішенні x(£_k , C) координата не задовольняє умові (29). Покажемо, що в цьому випадку вектор х(£_k , C) не задовольняє умовам (31, 32). Оскільки N_k – множина індексів небазисних змінних x_i, які в оптимальному рішенні дорівнюють нулю, то рівність (31) приймає вид і буде негативним відповідно до умови теореми. Отже, , тобто умова відсікання не виконується.

Перевіримо умову правильності. Для цього покажемо, що будь-яке припустиме рішення задачі (27-30) задовольняє умовам (31, 32).

Запишемо розкладання для координати припустимого рішення задачі (27-30) по небазисним змінним

(34)

і розглянемо два випадки: a) ; б) . Уведемо позначення:

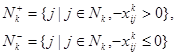
і представимо (34) у вигляді

де

Очевидно, тому що .

Розглянемо випадок а): , або що однаково, .

Звідси Але тому

(35)

Помножимо обидві частини (35) на ненегативну величину й складемо з ненегативною величиною :

(36)

Розглянемо випадок б): або, що однаково, Тому що по визначенню , то Помножимо обидві частини нерівності на ненегативну величину й на -1, одержимо . Додаючи до отриманого вираження нерівність , одержимо

(37)

Таким чином, в а) і в б) випадках прийшли до тому самому нерівності (36) і (37). Користуючись раніше уведеними позначеннями, їх можна записати

(38)

Формула (38) визначає правильні відсікання. Порівнюючи її з вираженням (31–32), доходимо висновку, що коефіцієнти визначаються в такий спосіб:

Теорема доведена.

Алгоритм Дальтона - Ллевелина може бути описаний у такий спосіб.

1. Вирішується (£_k , C) – задача (27–30) (спочатку k = 0). Нехай x(£_k , C), k = 0, 1, 2,…оптимальне рішення (£_k , C) – задачі, – симплексна таблиця.

2. Перевіряється умова допустимості по всіх координатах оптимального вектора рішення х(£_k , C) (£_k , C) – задачі. Якщо умова допустимості виконується, то отримане рішення є оптимальним рішенням вихідної задачі (27-30). Якщо умова допустимості не виконується хоча б по одній координаті, здійснюється перехід до 3.

3. Нехай не задовольняє умові допустимості. Тоді вибирається

i₀ = min {i| 1<i<n₁ , х_j0 ^k – не задовольняє (29)}.

4. Для обраного номера i=i₀ будується правильне відсікання, тобто вводиться додаткова змінна

де визначається формулою (33),

5. Додаємо лінійне обмеження, що визначає правильне відсікання, до умов (£_k , C) – задачі й одержуємо нову (£_{k+1, C) – задачу. Думаючи k = k + 1 , переходимо до п. 1.}

Приведемо без доказу теорему про кінцівку алгоритму.

Теорема. Якщо: коефіцієнти цільової функції дискретні; F(x) обмежена знизу на багатогранній множині £; задача (£, C) має принаймні одне рішення; вибір рядка для побудови правильного відсікання виробляється за правилом мінімального номера й (£_k , C) – задачі вирішуються методом послідовного уточнення оцінок, то алгоритм Дальтона й Ллевелина сходиться.

6. Алгоритм Данцига

Спосіб побудови правильних площин, що відтинають, запропонованим Данцигом значно простіше, ніж всі викладені вище способи. Але, як показали Гомори й Гофман, кінцівка алгоритму Данцига гарантується лише для дуже вузького класу задач. На прикладі алгоритму Данцига видно, наскільки тонким є питання про побудову правильних відсікань і як обережно варто підходити до різним спрощеним алгоритмам.

Розглядається повністю цілочисленна задача лінійного програмування:

Максимізувати

(39)

при умовах

(40)

(41)

– цілі, (42)

Ранг матриці вважаємо рівним m.

Теорема. Нехай x(£_r , C)=x^r є оптимальним опорним планом задачі (£_r , C) і x^r не задовольняє умові цілочисленності, N_r – множина індексів, що нумерують небазисні змінні, відповідні x^r .

Тоді нерівність

(43)

є правильним відсіканням.

Правильне відсікання, що відтинає нецілочисленний оптимум x(£_r , C) задачі (£_r , C) , можна записати в такий спосіб:

– ціле.

Помітимо, що кожна із знову змінних однозначно визначається завданням змінних , так що .

Позначимо через упорядковані в порядку зростання компоненти плану x задачі (39) – (41), так що

(44)

Покладемо

(45)

Лема. Якщо для деякого плану x задачі (39) - (41)

, (46)

те

(47)

Доказ проведемо по індукції. Спочатку доведемо, що

(47¢)

По визначенню

(48)

Тому що ранг матриці дорівнює m, те

де – число елементів множини . З визначення чисел одержуємо

(49)

(50)

З (48), (49), (50) і (46) маємо

Лема доведена при р=1 .

Тепер допустимо, що лема вірна при , і доведемо неї при :

Лема доведена.

Користуючись лемою, доведемо дві теореми.

Теорема 1 . Якщо кожний оптимальний план задачі (39) – (42) містить не менш (m+2) позитивних компонентів, то алгоритм Данцига не буде кінцевим.

Доказ. Допустимо, що на s-й ітерації алгоритму Данцига вийде шуканий оптимальний план . Розглянемо числа

(51)

Всі вони цілі й серед них повинне бути (n-m ) нулів – це небазисні змінні . Крім того, за умовою серед чисел , повинне бути принаймні (m+2) позитивні числа, тобто не більше чим (n-m- 2) нулів.

По визначенню чисел звідси треба, що

а тому що повинне бути цілим, те

(52)

Але по визначенню чисел

(53)

З (52) одержуємо

(54)

і по лемі

(55)

З (52), (53) і (55) треба, що серед чисел (51) принаймні [1+(m+1)+s] = [m+2+s] позитивних, а отже, не більше чим [n+s – (m+2+s)] = (n-m-2) нулів. Але вище було відзначено, що серед чисел (51) повинне бути (n-m) нулів. Вийшло протиріччя. Теорема 1 доведена.

Наслідок (з теореми 1). Для того щоб алгоритм Данцига був кінцевим, необхідно, щоб шуканий оптимальний план лежав на ребрі багатогранної множини (40) - (41) (передбачається, що задача (39) - (41) невиродженна).

Хоча ця умова і є досить твердим, йому задовольняють, наприклад, всі (невиродженні) задачі наступного виду.

Максимізувати

(56)

при умовах

(57)

(58)

(59)

– ціле, (60)

А це важливий клас задач.

Однак наведене в наслідку необхідна умова кінцівки алгоритму Данцига не є достатнім. Дійсно, має місце наступна

Теорема 2. Якщо для деякого оптимального плану x' задачі (39) - (42) і деякого плану x» задачі (39) - (41) мають місце нерівності

(61)

и

(62)

те алгоритм Данцига не буде кінцевим.

Доказ. Допустимо, що алгоритм Данцига кінцевий. Тоді з (61) треба, що крапка x» була відсічена на якійсь (скажемо, р-й ) ітерації, так що

(63)

Але з (62) і леми одержимо

(64)

Порівнюючи (63) і (64), одержуємо протиріччя. Теорема 2 доведена.

Отже, спрощений алгоритм Данцига буде кінцевим лише в досить рідких випадках.

7. Деякі висновки

Спробуємо охарактеризувати поводження алгоритмів методу відсікання при рішенні задач цілочисленного лінійного програмування. Як міра тривалості обчислень можуть розглядатися кількість симплексних ітерацій I і кількість правильних відсікань (додаткових лінійних обмежень) D.

Для першого алгоритму Гомори й різних його узагальнень I і D також тісно зв'язані між собою (як показує експеримент, у більшості випадків рішення окремої задачі (?, З) вимагає порівняно невеликої кількості симплексних ітерацій).

Переходимо до викладу окремих властивостей алгоритмів методу відсікання.

Числа I і D мають (у середньому) тенденцію до зростання зі збільшенням числа змінних і обмежень, ростом порядку коефіцієнтів задачі й збільшенням заповнювання матриці .

Це явище здається природним, але досвід показує, що в дискретному програмуванні «природне» і «правдоподібне» не завжди виявляється правильним. Точніше кажучи, досвід, накопичений на задачах ЛІНІЙНОГО ПРОГРАМУВАННЯ, не можна механічно переносити на задачі ЦІЛОЧИСЛЕННОГО ЛІНІЙНОГО ПРОГРАМУВАННЯ.

Насамперед, обертає на себе увага «нерегулярність», «непередбачуваність» поводження алгоритмів методу відсікання. Для ряду задач оптимальне рішення не вдавалося одержати після багатьох тисяч ітерацій, у той час як інші задачі вирішувалися за кілька десятків ітерацій.

Не вдається встановити безпосередній зв'язок між розмірами задач (тобто числом обмежень m і змінних n) і числом ітерацій: невдачі були зафіксовані навіть для невеликих задач (m?10, n?10), а успіхи - для задач досить великого розміру (m = 215, n = 2600). Можливо, втім, що спроба встановлення подібного зв'язку - це неправомірне перенесення результатів ЛІНІЙНОГО ПРОГРАМУВАННЯ в область ЦІЛОЧИСЛЕННОГО ЛІНІЙНОГО ПРОГРАМУВАННЯ.

Бути може, більше природною характеристикою задачі (£, З) є не число m лінійних обмежень, що задають багатогранну множину £, а число m ^ц - лінійних обмежень, що задають багатогранну множину V(£)*). Тим часом легко привести приклади, коли при невеликих m і n число m^ц буде досить велике.

«Нерегулярність» позначається й у наступному факті, поміченому поруч дослідників: іноді вдається істотно скоротити число ітерацій за рахунок перенумерації змінних.

Нарешті, має місце немонотонність наближення псевдоплана Х^r до оптимального плану X* – з ростом r відстань ρ(Х^r , X*) не обов'язково зменшується й лише на останній ітерації обов'язково стає рівним нулю.

Великий вплив на число ітерацій робить правило вибору рядка, що породжує. Тут також має місце «нерегулярність» - у той час як одне правило приводить до успіху за десятки ітерацій, інше не дає рішення після тисяч ітерацій.

При рішенні задач цілочисленного лінійного програмування по методу відсікання є як успіхи, так і невдачі.

До найбільш успішних робіт варто віднести:

1) Задачі покриття, у тому числі задачі, пов'язані з мінімізацією булевих функцій.

2) Застосування до задач оптимального кодування.

3) Застосування до задачі оптимального добування інформації з паралельних систем пам'яті.

Найбільш характерними задачами, для яких мала місце невдача, є:

1) Задачі комівояжера.

2) Задача теорії розкладів.

3) Деякі з узагальнених задач покриття.

У даний момент відсутнє вичерпне пояснення удач або невдач різних обчислювальних експериментів. Все-таки для задачі комівояжера й задачі теорії розкладів є правдоподібним наступне міркування.

Формулювання цих задач мовою ЦІЛОЧИСЛЕННОГО ЛІНІЙНОГО ПРОГРАМУВАННЯ є «неприродної». Для задачі порівняно невеликої в «природній» формулюванні, у моделі ЦІЛОЧИСЛЕННОГО ЛІНІЙНОГО ПРОГРАМУВАННЯ фігурує велика кількість обмежень і змінних. Можливо, що для цих задач більше перспективними є комбінаторні методи (наприклад, метод галузей і границь для задачі комівояжера). Втім, останнє твердження є спірним, тому що комбінаторні методи дуже чутливі до специфіки задач, введенню додаткових умов і т.п.

Очевидно, успіх у рішенні задач покриття пов'язаний з тим, що вдалося напасти на клас задач, практично важливих і в той же час успішно розв'язуваних. Було б досить цікаво точно охарактеризувати клас задач покриття, добре розв'язуваних по методу відсікання. Це тим більше цікаво, що побудовано приклади узагальнених задач покриття, для яких виникають значні обчислювальні труднощі.

І взагалі, виділення окремих класів ефективно розв'язуваних задач - важлива й цікава проблема.

Висновок

Підведемо деякі підсумки. Метод відсікання перебуває в стадії розвитку й удосконалювання. При реалізації цього методу виникають труднощі, що носять, очевидно, не тільки технічний, але й принциповий характер. У даний момент можна говорити про рішення за допомогою методу відсікання задач не більш ніж середнього розміру (сотні змінних і десятки обмежень).

Найбільш перспективними для подальших досліджень по методу відсікання представляються наступні напрямки:

1) Дослідження будови множин £^ц і V(£^ц) .

2) Дослідження властивостей правильних відсікань.

3) Вказівка нових способів побудови правильних відсікань.

4) Розвиток нових класів алгоритмів методу відсікання (наприклад, прямих алгоритмів).

5) Виділення окремих класів ефективно розв'язуваних задач.

Література

1. Корбут А.А., Финкельштейн Ю.Ю. Дискретне програмування. – К., 2004

2. Лященко І.Н. Лінійне й нелінійне програмування. – К., 2003

3. Санович К.М. Дослідження операцій. - К.,1999.