| Скачать .docx |
Реферат: Работа с массивами и решение систем уравнений в Mathcad
Содержание
Введение
1. Ранжированные переменные
2. Работа с массивами
3. Решение систем линейных уравнений
4. Решение нелинейных уравнений
5. Решение систем нелинейных уравнений
Заключение
Библиографический список
Введение
Одна из задач ЭВМ - автоматизация труда, повышение эффективности научных исследований. Основная особенность ЭВМ - ориентация на применение пользователями, не владеющими языками программирования. Такой подход позволяет преодолевать языковой барьер, отделяющий человека от машины. С этой целью разрабатываются пакеты прикладных программ, рассчитанные на широкие круги специалистов. К подобным пакетам относится MATHCAD.
MATHCAD - универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета - естественный математический язык, на котором формируются решаемые задачи.
Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.
Цель работы: изучение выполнения основных операций с массивами, решения систем линейных и нелинейных уравнений в Mathcad.
1. Ранжированные переменные
В математике часто возникает необходимость в задании некоторого ряда
значений. Например, при вычислении ![]() нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Для создания таких рядов в Mathcad используются ранжированные переменные
. В простом случае для создания ранжированной переменной используется выражение
нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Для создания таких рядов в Mathcad используются ранжированные переменные
. В простом случае для создания ранжированной переменной используется выражение
Name:=Nbegin…Nend,
Где Name – имя переменной, Nbegin – начальное значение переменной, Nend – ее конечное значение. Символ «…» (он вводится с клавиатуры знаком точка с запятой «;») указывает на изменение переменной в заданных границах. Если Nbegin<Nend, то шаг изменения переменной будет равен +1, в противном случае –1. Например, выражение a:=1…10 описывает ранжированную переменную a со значениями от 1 до 10.
Для создания ранжированной переменной общего вида используется выражение
Name:=Nbegin, (Nbegin+Step)…Nend,
где Step - заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend и отрицательным в противном случае).
Например, выражение a:=1, 1.5, …10 описывает ранжированную переменную a со значениями от 1 до 10 с шагом 0,5.
Ранжированные переменные широко применяются для представления функций в виде таблиц вывода , а также для построения их графиков.
Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка мышью на экране будет выведена таблица значений этого выражения. Такие таблицы называются таблицами вывода .
Необходимо учитывать следующее свойство таблиц вывода: если количество значений ранжированной переменной и, соответственно, строк в таблице вывода больше 16, то выводятся первые 16 строк. Если указатель мыши находится в пределах таблицы, то щелчок левой кнопкой мыши приводит к появлению вертикальной полосы прокрутки, позволяющей просмотреть все строки таблицы.
Помните, что задание ранжированных переменных эквивалентно заданию конечных циклов.
Примеры использования ранжированных переменных приведены на рисунке 1.1.

Рис. 1.1. Примеры использования ранжированных переменных
2. Работа с массивами
Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.
Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами . Для ввода индекса используется знак « [ » – прямая открывающая скобка.
Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V , либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.
В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.1.).

Рис. 2.1 Пример создания матриц без использования шаблонов матриц
Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.
| Оператор |
Ввод |
Описание |
V1+V2 |
V1+V2 |
Сложение векторов V1 и V2 |
V1-V2 |
V1-V2 |
Вычитание векторов V1 и V2 |
| -V |
-V |
Смена знака у элементов вектора V |
| -M |
-M |
Смена знака у элементов матрицы M |
| V-Z |
V-Z |
Вычитание из всех элементов вектора V скаляра Z |
| Z*V, V*Z |
Z*V, V*Z |
Умножение вектора V на скаляр Z |
| Z*M, M*Z |
Z*M, M*Z |
Умножение матрицы M на скаляр Z |
| V1*V2 |
V1*V2 |
Скалярное умножение векторов V1 и V2 |
| M*V |
M*V |
Умножение матрицы M на вектор V |
| M1*M2 |
M1*M2 |
Умножение матрицы M1 на матрицу M2 |
|
|
V/Z |
Деление всех элементов вектора V на скаляр Z |
|
|
M/Z |
Деление всех элементов матрицы M на скаляр Z |
| M-1 |
M^-1 |
Обращение матрицы M |
| Mn |
M^n |
Возведение матрицы M в степень n |
| |V| |
|V |
Вычисление модуля вектора V |
| |M| |
|M |
Вычисление определителя матрицы M |
| VT |
V Ctrl+! |
Транспонирование вектора V |
| MT |
M Ctrl+! |
Транспонирование матрицы M |
| V1´V2 |
V1 Ctrl+* V2 |
Векторное умножение векторов V1 и V2 |
|
|
Alt+$ V |
Вычисление суммы элементов вектора V |
| M<n> |
M Ctrl+^ n |
Выделение n-ого столбца матрицы M |
| Vn |
V[n |
Выделение n-ого элемента вектора V |
| Mm,n |
M[(m,n) |
Выделение элемента (m, n) матрицы M |
Существует ряд встроенных векторных и матричных функций . Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц.
| length(V) |
возвращает число элементов вектора |
| last(V) |
возвращает номер последнего элемента вектора |
| max(V) |
возвращает максимальный по значению элемент вектора или матрицы |
| min(V) |
возвращает минимальный по значению элемент вектора или матрицы |
| augment(M1,M2) |
объединяет в одну две матрицы, имеющие одинаковое число строк (объединение идет бок о бок) |
| identity(n) |
создает единичную квадратную матрицу размером n*n |
| stack(M1,M2) |
объединяет в одну две матрицы, имеющие одинаковое число столбцов, располагая М1 над М2 |
| submatrix(A,ir,jr,ic,jc) |
возвращает субматрицу, состоящую из всех элементов содержащихся в строках от ir по jr и столбцов с ic по jc (ir£jr и ic£jc) |
| diag(V) |
создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора V |
| matrix(m,n,f) |
создает матрицу, в которой (i, j) элемент равен f(i,j), где i=0, 1, …, m и j=0, 1, …, n; f(i,j) - некоторая функция |
| cols(M) |
возвращает число столбцов матрицы M |
| rows(M) |
возвращает число строк матрицы M |
| rank(M) |
возвращает ранг матрицы M |
| tr(M) |
возвращает след (сумму диагональных элементов) матрицы M |
| mean(M) |
возвращает среднее значение элементов матрицы M |
Примеры работы с матрицами приведены на рисунке 2.2.

Рис. 2.2. Примеры работы с матрицами
3. Решение систем линейных уравнений
Векторные и матричные операторы и функции позволяют решать широкий круг задач линейной алгебры.
Например, если задана матрица A и вектор B для системы линейных уравнений в матричной форме ![]() , то вектор решения X
можно получить из уравнения
, то вектор решения X
можно получить из уравнения ![]() .
.
Поскольку решение систем линейных уравнений довольно распространенная задача, то в Mathcad введена специальная функция lsolve(A,B)
, которая возвращает вектор X для системы линейных уравнений ![]() при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A - n´n.
при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A - n´n.
Пусть необходимо решить систему уравнений
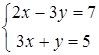 .
.
В нашем случае матрицы A и B определяется следующим образом:
 ,
,  . Два способа решения этой системы уравнений в Matcad приведены на рисунке 2.3.
. Два способа решения этой системы уравнений в Matcad приведены на рисунке 2.3.

Рис. 2.3. Примеры решения системы линейных уравнений
4. Решение нелинейных уравнений
Многие уравнения, например трансцендентные, не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной TOL).
Для уравнений вида ![]() решение находится с помощью следующей функции:
решение находится с помощью следующей функции:
root(Выражение, Имя_переменной).
Эта функция возвращает с заданной точностью значение переменной, при котором выражение равно 0. Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно если уравнение имеет несколько корней.
Для поиска корней полинома степени n существует специальная функция polyroots(V) . Она возвращает вектор всех корней полинома степени n, коэффициенты которого находятся в векторе V, который имеет длину n+1. Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой, поскольку в этом случае трудно получить малую погрешность вычисления корней.
Пример использования функции root приведен на рисунке 2.4, а функции polyroots - на рисунке 2.5.

Рис. 2.4. Пример использования функции root

Рис. 2.5. Пример использования функции polyroots
5. Решение систем нелинейных уравнений
При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый директивой Given и имеющий следующую структуру:
- Начальные условия (задаются в виде переменная:=значение ).
- Директива Given.
- Уравнения.
- Ограничительные условия.
- Выражения с функциями Find, Minerr, Maximize, Minimize .
Начальные условия определяют начальные значения искомых переменных. Они задаются обычным присваиванием переменным начальных значений. Если переменных несколько, то используется векторное представление для начальных значений. Уравнения задаются в виде expr_left=expr_right с применением жирного знака равно = между левой и правой частью каждого уравнения (вводится с клавиатуры как Ctrl+= или панели булевых операторов). Ограничительные условия обычно задаются в виде неравенств и равенств, которые должны удовлетворяться при решении уравнений.
В блоке используется одна из следующих функций:
- Find(v1,v2,…,vn) - возвращает значение одной или ряда переменных для точного решения;
- Minerr(v1,v2,…,vn) - возвращает значение одной или ряда переменных для приближенного решения.
Между этими функциями существует принципиальное различие. Первая функция используется, когда решение реально существует, хотя и не является аналитическим. Вторая функция пытается найти наилучшее приближение даже к несуществующему значению путем минимизации среднеквадратичной погрешности решения.
Логические операторы в качестве ограничительных условий вводятся следующим образом:
| Оператор |
Клавиши |
Описание |
| e1>e2 |
e1>e2 |
e1 больше e2 |
| e1<e2 |
e1<e2 |
e1 меньше e2 |
| e1³e2 |
e1 Ctrl+) e2 |
e1 больше или равно e2 |
| e1£e2 |
e1 Ctrl+( e2 |
e1 меньше или равно e2 |
| e1¹e2 |
e1 Ctrl+# e2 |
e1 не равно e2 |
| e1=e2 |
e1 Ctrl+= e2 |
e1 равно e2 |
В качестве примера рассмотрим решение (рис. 2.6.) следующей системы нелинейных уравнений:
 .
.
mathcad матрица уравнение линейный

Рис. 2.6. Пример решения системы нелинейных уравнений
При решении системы нелинейных уравнений с использованием функции Minerr надо проявлять осторожность и обязательно проверять полученное решение. Нередки случаи, когда решения могут оказаться ошибочными. Полезно как можно точнее указывать начальные приближения к решению.
Заключение
И так, перечислим основные достоинства MATHCAD`a.
Во-первых, это универсальность пакета MATHCAD, который может быть использован для решения самых разнообразных инженерных, экономических, статистических и других научных задач.
Во-вторых, программирование на общепринятом математическом языке позволяет преодолеть языковой барьер между машиной и пользователем. Потенциальные пользователи пакета - от студентов до академиков.
И в-третьих, совместно применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ.
Но, к сожалению, популярный во всем мире пакет MATHCAD фирмы MathSoft, в России распространен еще слабо, как и все программные продукты подобно рода.
Библиографический список
1. Дьяконов В.П. Matcad 8/2000: Специальный справочник. - СПб.: Питер, 2001. - 592 с.
2. Артемкин Д.Е., Пылькин А.Н. Основы работы в системе MATHCAD. Рязань: Рязанский областной институт развития образования, 1999. - 72 с.
3. Соломоник В.С. Сборник вопросов и задач по математике. - М.: Высшая школа, 1978. - 264 с.
4. Гусев В.А., Мордкович А.Г. Математика : Справочные материалы. - М.: Просвещение, 1988. - 416 с.