| Скачать .docx |
Курсовая работа: Пошук найкоротшого шляху на орієнтованому графі
Міністерство освіти і науки України
Національний університет «Львівська Політехніка»
Кафедра автоматизованих систем управління
Курсова робота
з дисципліни «Проблемно-орієнтовані мови програмування»
на тему
Пошук найкоротшого шляху на орієнтованому графі
Виконав:
Студент групи КН-22з
Василашко Володимир
Керівник:
Кустра Н.О.
Львів 2011
Міністерство освіти та науки України
Національний університет «Львівська політехніка»
Кафедра автоматизованих систем управління
Завдання на курсову роботу
з дисципліни «Проблемно-орієнтовні мови програмування»
Прізвище,ім’я студента Василашко Володимир
Група КН-22з
Тема курсової роботи Пошук найкоротшого шляху на орієнтованому графі
Зміст
Вступ
1.Постановка завдання та сфераїїзастосування
2. Теоретичначастина
2.1 Загальнівідомостіпрографи
2.2 АлгоритмДейкстри
3. Особливості роботи всередовищі
4. Програмнареалізація
4.1 Описалгоритмута структурипрограми
4.2 Опис програмнихзасобів
5. Інструкціякористувача
Висновок
Перелікпосилань
ДодатокАТекстпрограми
ДодатокБРезультат
ДодатокВСхемапрограмноїреалізаціїалгоритмуДейкстри
ВСТУП
Завдяки своєму широкому застосуванню, теорія про знаходження найкоротших шляхів останнім часом інтенсивно розвивається. Знаходження найкоротшого шляху - життєво необхідно і використовується практично скрізь, починаючи від перебування оптимального маршруту між двома об'єктами на місцевості (наприклад, найкоротший шлях від будинку до університету), в системах автопілота, для знаходження оптимального маршруту при перевезеннях, комутації інформаційного пакету в Internet і т. д. Найкоротший шлях розглядається за допомогою певного математичного об'єкту, званого графом. Існують три найбільш ефективних алгоритму знаходження найкоротшого шляху:
• алгоритм Дейкстри (використовується для знаходження оптимального маршруту між двома вершинами);
• алгоритм Флойда (для знаходження оптимального маршруту між усіма парами вершин);
• алгоритм Йена (перебування k-оптимальних маршрутів між двома вершинами).
Зазначені алгоритми легко виконуються при малій кількості вершин у графі. При збільшенні їх кількості завдання пошуку найкоротшого шляху ускладнюється. Тут на допомогу приходить сучасна техніка. Комп'ютерні засоби та інформаційні технології підвищили можливості такого всеосяжного методу вивчення і створення, як моделювання об'єктів, явищ і процесів - як тих, що існують у природі, так і тих, що створюються людиною штучно. Кількість об'єктів ускладнювалися, збільшувалися, і натурне моделювання (макети споруд) стало невигідним, не економним. Тому для вивчення почали застосовувати математику. Використання математичних моделей - рівняння, нерівності, формули і тому подібне називається математичним моделюванням, для розвитку і пристосування якого потрібні були ефективні чисельні методи. Реалізувати великий потенціал математичного моделювання неможливо без потужних засобів автоматизації обчислень, якими є комп'ютери. Завдяки появі комп'ютерів і розвитку інформаційних технологій створюються методи та засоби комп'ютерного моделювання, здатні вирішувати складні практичні завдання, такі як управління великими енергетичними системами, створення достовірних прогнозів погоди або врожаю, моделювання регіональних і загальнодержавних систем, проектування літаків, кораблів тощо. Комп'ютерна модель - це розміщена в комп'ютері сукупність засобів, що реалізують концепцію обчислення. Для реалізації комп'ютерної моделі, велике значення має такий науковий напрямок, як програмування. Без нього комп'ютер це просто набір різних пристроїв, мікросхем, який не може бути корисним. Великі програми із-за своєї складності нерідко містять помилки, які можуть стати причиною матеріальних збитків, а іноді й загрожувати життю людей (наприклад, при управлінні авіапольотом). У результаті боротьби з проблемою складності програмного коду були вироблені три нові концепції програмування: а) об'єктно-орієнтоване програмування (ООП); б) уніфікована мова моделювання (UML); в) спеціалізовані засоби розробки програмного забезпечення; З усіх об'єктно-орієнтованих мов С + + є найбільш широко використовуваним. І саме з його допомогою в даному курсовому проекті реалізується алгоритм Дейкстри.
1. ПОСТАНОВКА ЗАВДАННЯ І СФЕРА ЇЇ ЗАСТОСУВАННЯ
Основним завданням даного курсового проекту є програмна реалізація алгоритму пошуку найкоротшого шляху між двома будь-якими вершинами графа. Програма повинна працювати так, щоб користувач вводив кількість вершин і довжини ребер графа, а після обробки цих даних на екран виводився найкоротший шлях між двома заданими вершинами і його довжина. Необхідно передбачити різні результати пошуку, щоб програма не видавала помилок і працювала правильно. Дана програма може використовуватися в дискретної математики для дослідження графів або в якості наочного посібника, що демонструє застосування алгоритму Дейкстри на практиці. алгоритм дейкстри граф найкоротший шлях
2. ТЕОРЕТИЧНА ЧАСТИНА
2.1 Відомості про графи
Граф G (рис.2.1.1) задається множиною точок (вершин) х1 , х2 ,..., хn . (Яке позначається через Х) і безліччю ліній (ребер) а1 , а2 ,...,аm . (Яке позначається символом А), що з'єднують між собою всі або частину цих точок. Таким чином, граф G повністю задається (і позначається) парою (Х, А). Якщо ребра з множини А орієнтовані, що зазвичай показується стрілкою, то вони називаються дугами, і граф з такими ребрами називається орієнтованим графом.
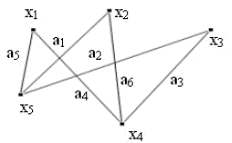 Рис.2.1.1
Рис.2.1.1 
Рис.2.1.2
Наприклад, якщо дорога має не двохсторонній, а односторонній рух то напрямок цього руху буде показано стрілкою. Якщо ребра не мають орієнтації, то граф називається неорієнтованим, (двосторонній рух). У орієнтованому графі дуга позначається впорядкованої парою, що складається з початкової та кінцевої вершин, її напрямок передбачається заданим від першої вершини до другої.
Шляхом (або орієнтованим маршрутом) орієнтованого графа називається послідовність дуг, в якій кінцева вершина будь-якої дуги, відмінною від останньої, є початковою вершиною наступної.
Так, на рис. 2.1.2 шляхами є послідовності дуг: а6 , а5 , а9 , а8 , а4. (1) а1 , а6 , а5 , а9 . (2) а1 , а6 , а5 , а9 , а10 , а6 , а4 . (3) Орієнтованої ланцюгом (орцепью) називається такий шлях, в якому кожна дуга використовується не більше одного разу. Простим ланцюгом називається такий шлях, в якому кожна вершина використовується не більше одного разу. Наприклад, шлях (2). Маршрут є неорієнтований "двійник" шляху, і це поняття розглядається в тих випадках, коли можна знехтувати спрямованістю дуг у графі. Таким чином, маршрут є послідовність ребер ä1 , ä2 ,..., äq , в якій кожне ребро аi , за винятком першого і останнього ребер, пов'язане з ребрами аi-1 і аi+1 своїми кінцевими вершинами. Послідовності дуг: ä2 , ä4 , ä8 , ä10 , (4) ä2 , ä7 , ä8 , ä4 , ä3 , (5) ä10 , ä7 , ä4 , ä8 , ä7 , ä2 . (6) у графі, зображеному на рис. 2.1.2, є маршрутами; дві точки над символом дуги означають, що її орієнтацією нехтують, тобто дуга розглядається як неорієнтовані ребро. Також шлях або маршрут можна зображати послідовністю вершин. Наприклад, шлях (1) буде виглядати наступним чином: х2 , х5 , х4 , х3 , х5 , х6 . Іноді дуг графа приписуються числа, що називаються вагою, вартістю, або довжиною цієї дуги. У цьому випадку граф називається графом із завислими дугами. А якщо вага приписується вершин графа, то тоді виходить граф з зваженими вершинами. Якщо в графі ваги приписані і дуг і вершин, то він називається просто зваженим. При розгляді шляху μ представленого послідовністю дуг (ä1 , ä2 ,..., äq ), за його вага приймається число l (μ), яка дорівнює загальній кількості ваг всіх дуг, що входять в μ, тобто
![]()
2.2 Алгоритм Дейкстри
Алгоритм Дейкстри будує найкоротші шляхи, що ведуть з вихідної вершини графа до решти вершин цього графа (якщо такі є). У процесі роботи алгоритму послідовно позначаються розглянуті вершини графа. При чому вершина, позначена останньої (на даний момент) розташована ближче до вихідної вершині, ніж всі непозначених, але далі, ніж всі помічені. Спочатку позначається вихідна вершина; наступної, очевидно, буде позначена вершина, найближча до початкової, і суміжна з нею. Нехай на якомусь кроці вже позначені кілька вершин. Відомі найкоротші шляхи, що ведуть з вихідної вершини до поміченої. Для кожної з непозначених вершин проробимо наступне: 1. Розглянемо всі дуги, провідні з помічених вершин в одну непозначених. Кожна така дуга є останньою дугою на шляху з вихідної вершини в цю непозначену. 2. Виберемо з цих шляхів найкоротший. А потім виберемо серед них самий короткий до всіх непозначених вершин, і позначимо вершину, до якої він веде. Алгоритм завершиться, коли будуть помічені всі досяжні вершини. У результаті роботи алгоритму Дейкстри будується Дерево найкоротших шляхів.
3. ОСОБЛИВОСТІ РОБОТИ В СЕРЕДОВИЩІ
При написанні програми використовувалася середу Microsoft Visual C + + 6.0. Дане середовище дозволяє писати програми на мові C + +. У ході написання програми всі оператори і службові слова мови С + + виділяються іншим кольором, щоб відрізняти їх від змінних, заданих програмістом. Середовище Microsoft Visual C + + 6.0 містить вбудований компілятор. Вікно програми розділене на декілька частин. Вгорі знаходиться стандартна панель - Standart, з якою можна зберегти вихідний текст програми на диск, відкрити новий документ, скопіювати або вставити текст, скасувати останню дію, або знайти текст. Зліва знаходяться панелі Object TreeView і Object Inspector, на яких показані об'єкти, які використовуються в даній програмі, та їх властивості. У центрі вікна програми розташований текстовий редактор, в якому слід писати програму. Внизу - панель Output, в якій показується повідомлення, якщо в програмі містяться помилки - компілятор повідомляє вид помилки і рядок, в якій вона допущена, досить зробити подвійний клік лівою клавішею миші на описі помилки в Output, щоб переміститися на рядок, що містить помилки. Програма створена в консольному режимі - в режимі, що не має графічного інтерфейсу.
4 ПРОГРАМНА РЕАЛІЗАЦІЯ
4.1 Опис алгоритму та структури програми
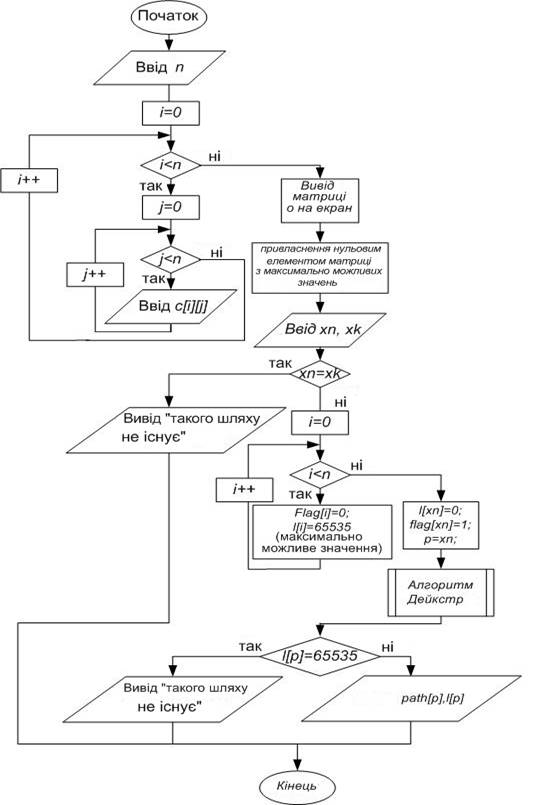
Рис.4.1.1
Програма виводить мінімальний шлях між двома зазначеними вершинами у графі і його довжину. При запуску програми на екран виводиться запит про введення ваг ребер досліджуваного графа. Дані, введені користувачем, відображаються у вигляді матриці суміжності, в якій не існуючі ребра позначаються нулями. Після зазначеним ребрах присвоюється значення 65535, яке приймається за нескінченність. Наступним етапом виконання програми є запит про введення номерів вершин, між якими необхідно дізнатися шлях. У випадку, якщо початкова та кінцева вершини співпадають, з'являється повідомлення і робота програми завершується. В іншому випадку виконується безпосередньо алгоритм Дейкстри, схема якого наведена у додатку В. Результатом програми є вивід на екран вершин, через які проходить мінімальний шлях, а також виведення довжини маршруту. Якщо шляху між заданими точками не існує - виводиться відповідне повідомлення.
4.2 Опис використаних програмних засобів
Таблица 4.2.1–Опис змінних
| Змінна | Тип | Опис |
| n | int | Кількість точок (вершин) графа |
| i,j | int | Лічильники |
| p | int | Номер найкоротшого шляху і найменшої довжини шляху |
| xn | int | Номер початкової точки (вершини) |
| xk | int | Номер кінцевої точки (вершини) |
| flag[11] | int | Масив, i-й елемент якого має значення 0, коли i-й шлях і відстань тимчасові, і приймає значення 1, коли i-й шлях і відстань стають постійними |
| c[11][11] | word (unsigned int) | Масив i-j елемент якого містить відстань між i-й і j-й крапками (вершинами)Зауваження: 1. с[i][i]=¥ 2. c[i][j]=c[j][i] |
| s[80] | char | Рядкова змінна, яка містить проміжні значення шляху |
| path[80][11] | char | Масив рядків, який містить шляхуЗауваження:Після проходження обробки за алгоритмом Дейкстри p-й елемент масиву містить найкоротший шлях. |
| l[11] | word (unsigned int) | Масив, який містить довжини шляхів (path)Зауваження:Після проходження обробки за алгоритмом Дейкстри p-й елемент масиву містить довжину найкоротшого шляху. |
Крім стандартних функцій з бібліотек iostream.h, string.h, stdio.h, conio.h були використані також наступні функції.• word minim (word x, word y) - функція, яка повертає мінімальне з x і y.
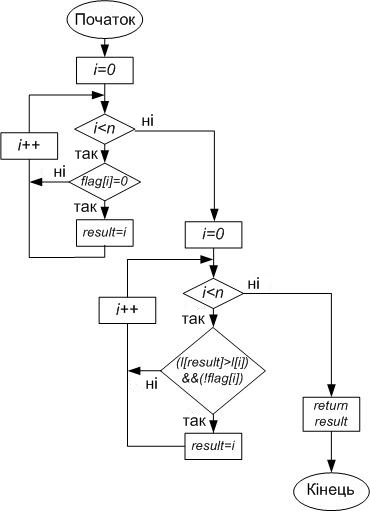
Рис.4.2.1
• int min (int n) - функція, яка повертає номер елемента масиву l [i] мінімальної «невідмічений» довжиною шляху (flag [i] = 0).
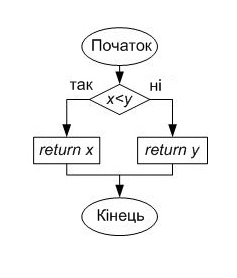
Рис.4.2.2
5. ІНСТРУКЦІЯ КОРИСТУВАЧА
При запуску програми на екрані з'явиться вікно з інструкціями. Виконуйте ці інструкції, а саме: 1. Введіть кількість вершин досліджуваного графа. 2. Введіть ваги ребер (позитивне число). У програмі відстані від хi до xi+1 та xi+1 до хi вважаються рівними, а відстані від хi до хi - не існуючими. Якщо ребра між зазначеними вершинами не існує, введіть 0 (нуль). На екран виводиться матриця суміжності, що відображає введену інформацію. 3. Введіть номер вершини, від якої починається шуканий шлях. 4. Введіть номер вершини, у якій шлях закінчується. 5. Щоб завершити роботу програми після отримання результату натисніть Enter.
ВИСНОВОК
Таким чином, в процесі створення даного проекту розроблена програма, що реалізує алгоритм Дейкстри в Microsoft Visual C + + 6.0. Її недоліком є примітивний користувальницький інтерфейс. Це пов'язано з тим, що програма працює в консольному режимі, не додає до складності мови складність програмного віконного інтерфейсу. Також були поглиблені знання, отримані в процесі виконання лабораторних робіт з предмету «Програмування».
ПЕРЕЛІК ПОСИЛАННЯ
1. Бондарєв В.М. Програмування на С + + .- Х: «Компанія СМІТ», 2004
2. Страуструп Бьярн Мова програмування С + + (2 рік) .- «К: ДіаСофт», 1993
3. Хаханов В.І., Чумаченко С.В. Дискретна математика (теоретичне І практичне Зміст курсу) .- Кафедра АПОТ, 2002
4. Алгоритм Дейкстри
5. Конспект лекцій.
Додаток А
Текст програми
#include<iostream.h>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define word unsigned int
int i, j, n, p, xn, xk;
int flag[11];
word c[11][11], l[11];
char s[80], path[80][11];
int min(int n)
{
int i, result;
for(i=0;i<n;i++)
if(!(flag[i])) result=i;
for(i=0;i<n;i++)
if((l[result]>l[i])&&(!flag[i])) result=i;
return result;
}
word minim(word x, word y)
{
if(x<y) return x;
return y;
}
void main()
{
cout<<"Vvedit` kil`kist` tochok: ";
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++) c[i][j]=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
cout<<"Vvedit` vidstan` vid x"<<i+1<<" do x"<<j+1<<": ";
cin>>c[i][j];
}
cout<<" ";
for(i=0;i<n;i++) cout<<" X"<<i+1;
cout<<endl<<endl;
for(i=0;i<n;i++)
{
printf("X%d",i+1);
for(j=0;j<n;j++)
{
printf("%6d",c[i][j]);
c[j][i]=c[i][j];
}
printf("\n\n");
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(c[i][j]==0) c[i][j]=65535; //безкінечнність
cout<<"Vvedit` pochatkovi tochku: ";
cin>>xn;
cout<<"Vvedit` kincevi tochku: ";
cin>>xk;
xk--;
xn--;
if(xn==xk)
{
cout<<"Pochatkova i kinceva tochku spivpadayut`."<<endl;
getch();
return;
}
for(i=0;i<n;i++)
{
flag[i]=0;
l[i]=65535;
}
l[xn]=0;
flag[xn]=1;
p=xn;
itoa(xn+1,s,10);
for(i=1;i<=n;i++)
{
strcpy(path[i],"X");
strcat(path[i],s);
}
do
{
for(i=0;i<n;i++)
if((c[p][i]!=65535)&&(!flag[i])&&(i!=p))
{
if(l[i]>l[p]+c[p][i])
{
itoa(i+1,s,10);
strcpy(path[i+1],path[p+1]);
strcat(path[i+1],"-X");
strcat(path[i+1],s);
}
l[i]=minim(l[i],l[p]+c[p][i]);
}
p=min(n);
flag[p]=1;
}
while(p!=xk);
if(l[p]!=65535)
{
cout<<"Shljah: "<<path[p+1]<<endl;
cout<<"Dovjuna shljahy: "<<l[p]<<endl;
}
else
cout<<"takogo shljahy ne isnye!"<<endl;
getch();
}
Додаток Б
Результат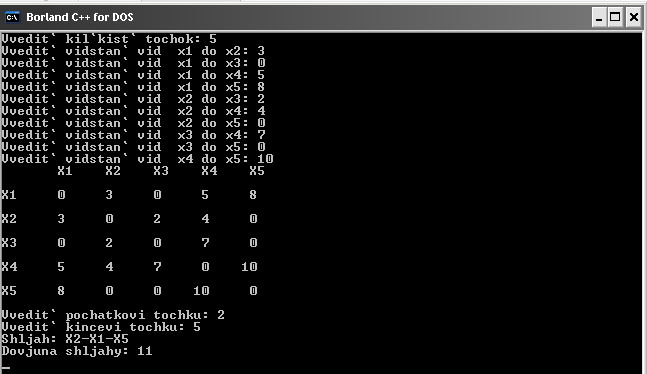
Додаток В
Схема програмної реалізації алгоритму Дейкстри
