| Скачать .docx |
Курсовая работа: Разработка системы для оценки перспективности производственных направлений на предприятии
Задание на курсовой проект по курсу «Экономическая кибернетика»
Исходные данные: Предприятие, производящее компьютеры.
На предприятии есть пять основных направлений:
1) PC Производство настольных рабочих станций
2) CР Производство серверов
3) CO Производство сетевого оборудования
4) КП Производство компьютерной периферии
5) НБ Производство ноутбуков
Производство линейно.
Структура технологических связей
| PC | CP | CO | КП | НБ | |
| PC | 0,111 | 0,111 | 0,083 | 0,083 | 0,200 |
| CP | 0,090 | 0,117 | 0,071 | 0,166 | 0,100 |
| CО | 0,090 | 0,125 | 0,071 | 0,090 | 0,083 |
| КП | 0,076 | 0,166 | 0,100 | 0,058 | 0,111 |
| НБ | 0,076 | 0,100 | 0,083 | 0,071 | 0,111 |
Всего на предприятии работает 3000 человек, структура распределения трудовых ресурсов на производство единицы продукции следующая:
| PC | CP | CO | КП | НБ |
| 0,020 | 0,054 | 0,007 | 0,020 | 0,030 |
Требуется:
1) Составить таблицу попарных сравнений, исходя из имеющегося спроса на рынке каждого вида продукции. Оценить математически согласованность таблицы.
2) Определить приоритеты для производства каждого вида продукции и на основании этих приоритетов рассчитать предварительный режим работы производства, считая, что всего на предприятии ежемесячно производится 100000 единиц оборудования.
3) Оценить является ли производство продуктивным. При непродуктивном производстве внести в технологическую матрицу необходимые коррективы.
4) Учитывая имеющиеся ограничения на трудовые ресурсы рассчитать максимально возможный столбец выпуска добавочной стоимости.
5) Для каждого вида продукции рассчитать оптимальную ценовую политику. Для расчета ценовой политики использовать самостоятельно составленные статистические данные о продажах.
6) Сделать вывод, о том какие три из шести из подразделений являются наиболее перспективными.
СОДЕРЖАНИЕ
Введение
1 Описание используемых математических методов и моделей
1.1 Анализ иерархий и приоритетов
1.2 Метод Крылова
1.3 Метод Ньютона (метод касательных
1.4 Метод Гаусса для решения систем уравнений
2 Обоснование выбора программной платформы
3 Описание разработанных программных модулей
3.1 Интерфейс пользователя функциональной подсистемы
3.2 Анализ полученных результатов
Выводы
Список литературы
ВВЕДЕНИЕ
В условиях рыночной системы управления производственной и сбытовой деятельностью предприятий и фирм в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе основой предпринимательской деятельности становится изучение потребительского спроса.
Кибернетика характеризуется новыми подходами к анализу и синтезу сложных динамических объектов. Системный подход, позволяет рассматривать явление во всей его сложности, с учетом всех имеющихся связей и свойств. Вместе с тем, развитие кибернетики потребовало переосмысления некоторых старых понятий, сложившихся в общественной практике, и формализации представлений терминологического характера, являющихся исходной базой при изучении сложных систем управления различной природы.
Целью данного курсового проекта является разработка системы для оценки перспективности производственных направлений на предприятии.
Для достижения поставленной цели следует разработать ряд взаимосвязанных программных модулей, а именно:
- модуль подготовки данных;
- модуль формирования режима работы производства, на основе оценки приоритетов;
- модуль расчета максимально возможного выпуска добавочной стоимости, с использованием модели Леонтьева;
- модуль определения оптимальной ценовой политики для видов продукции.
1. ОПИСАНИЕ ИСПОЛЬЗУЕМЫХ МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
1.1 Анализ иерархий и приоритетов
Метод анализа иерархий является замкнутой логической конструкцией, которая обеспечивает с помощью простых и хорошо обоснованных правил, решение многокритериальных задач, включающих как качественные, так и количественные факторы, причем количественные факторы могут иметь разную размерность. Метод основан на декомпозиции задачи и представлении ее в виде иерархической структуры, что позволяет включить в иерархию все имеющиеся у лица, принимающего решение знания по решаемой проблеме и последующей обработке суждений лиц, принимающих решения. В результате может быть выявлена относительная степень взаимодействия элементов в иерархии, которые затем выражаются численно. Метод анализа иерархий включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений.
Весь процесс решения подвергается проверке и переосмыслению на каждом этапе, что позволяет проводить оценку качества полученного решения.
Первый этап - предусматривает представление проблемы в виде иерархии или сети. В простейшем случае иерархия строится начиная с цели, которая помещается в вершину иерархии. Через промежуточные уровни, на которых располагаются критерии и от которых зависят последующие уровни, к самому низкому уровню, который содержит перечень альтернатив.
Второй этап. После иерархического представления задачи необходимо установить приоритеты критериев и оценить каждую из альтернатив по критериям, определив наиболее важную их них.
В методе анализа иерархий элементы сравниваются попарно по отношению к их влиянию на общую для них характеристику. Парные сравнения приводят к записи характеристик сравнений в виде квадратной таблицы чисел, которая называется матрицей.
Сравнивая набор критериев, друг с другом, формируется обратно симметричная матрица попарных сравнений, которая имеет вид :
 (1.1.1)
(1.1.1)
Когда задача представлена в виде иерархической структуры, матрица составляется для попарного сравнения критериев на втором уровне по отношению к общей цели, расположенной на первом уровне. Такие же матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня и т.д., если количество уровней больше трех.
Для проведения субъективных парных сравнений в методе анализа иерархий используется шкала, представленная в таблице 1.1.
Таблице 1.1— Шкала относительной важности
| Интенсивность относительной важности | Определение | Объяснение |
| 1 | Равная важность | Равный вклад двух критериев в цель. |
| 3 | Умеренное превосходство одного над другим. | Опыт и суждения дают легкое превосходство одной альтернативы над другой |
| 5 | Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одного критерия над другим |
| 7 | Значительное превосходство | Одному из критериев дается настолько сильное предпочтение, что оно становится практически значительным |
| 9 | Очень сильное превосходство | Очевидность превосходства одного критерия над другим подтверждается наиболее сильно |
| 2,4,6,8 | Промежуточные решения между двумя соседними суждениями | Применяется в компромиссных случаях |
Существует понятие индекс согласованности (ИС), который дает информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице.
ИС = (l max - n)/(n - 1) (1.1.2)
В рамках данной курсовой работы в качестве критерия для сравнения видов продукции использовались статистические данные по продажам (спросу) на рынке. Данные по продажам представлены в таблице 1.2.
Таблица 1.2 - Статистические данные по продажам продукции предприятия
| Виды | РС | СР | СО | КП | НБ | Итого |
| 5270 | 240 | 730 | 1150 | 2610 | 10000 |
Пояснение к сокращениям:
РС - Производство настольных рабочих станций
СР - Производство серверов
СО - Производство сетевого оборудования
КП - Производство компьютерной периферии
НБ - Производство ноутбуков
Для определения значений попарных сравнений воспользуеся соотношением (1.2).
![]() , где (1.1.3)
, где (1.1.3)
![]() - сравнение i-го и j-го вида продукции, dj
– спрос на j-й вид продукции.
- сравнение i-го и j-го вида продукции, dj
– спрос на j-й вид продукции.
Таким образом, таблица попарных сравнений будет иметь вид
| РС | СР | СО | КП | НБ | |
| РС | 1 | 10 | 2,857 | 1,818 | 0,596 |
| СР | 0,017 | 1 | 0,114 | 0,122 | 0,027 |
| СО | 0,03 | 1,4 | 1 | 0,256 | 0,093 |
| КП | 0,089 | 2,142 | 0,624 | 1 | 0,147 |
| НБ | 0,219 | 6 | 1,688 | 1,091 | 1 |
Из таблицы видно, что Рабочие станции по сравнению с Серверами оценены как 10, соответственно Сервера по сравнению Рабочими станциями в 0,017.
Анализ приоритетов производится с использованием «Модуля формирования режима работы производства, на основе оценки приоритетов».
1.2 Метод Крылова
Метод Крылова основан на свойстве квадратной матрицы М обращать в нуль свой характеристический многочлен. В данной работе матрица М -это матрица коэффициентов технологических связей, которая имеет вид:

Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль. Пусть (1.2.1) характеристический многочлен
![]() (1.2.1)
(1.2.1)
Заменяя в выражении величину λ на M, получаем
![]() (1.2.2)
(1.2.2)
Взяв произвольный ненулевой вектор У0 и умножив обе части выражения (1.2.2) на него, получим:
![]() (1.2.3)
(1.2.3)
Положим
![]()
![]() (1.2.4)
(1.2.4)
Тогда
![]() (1.2.5)
(1.2.5)
Или в виде

Если эта система имеет единственное решение, то ее корни р1 , р2 …..рn , являются коэффициентами характеристического многочлена (1.2.1).
Если известны коэффициенты р1 , р2 …..рn , и корни λ1 , λ2 ,….λn характеристического многочлена, то метод Крылова дает возможность найти соответствующие векторы по следующей формуле:
![]() ,
, ![]() (1.2.6)
(1.2.6)
Здесь y(
n
-1)
, y(
n
-2)
, …. y(0)
– векторы, использованные при нахождении коэффициентов р1
, р2
…..рn
методом Крылова, а коэффициенты qij
(![]()
![]() ) определяются по схеме Горнера
) определяются по схеме Горнера
q0i = 1, qij = λi qi-1,i +pi (1.2.7)
Для определения собственных чисел матрицы М необходимо решить полученное характеристическое уравнение. Для матрицы М это уравнение будет пятой степени, решать такое уравнение в данной работе будем решать, используя метод касательных или иначе метод Ньютона.
1.3 Метод Ньютона (метод касательных)
Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Чтобы численно решить уравнение f (х) = 0 методом простой итерации, его необходимо привести к следующей форме: х = f(х), где f (х) -сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения ![]() должно выполняться условие
должно выполняться условие ![]() . Решение данного уравнения ищут в виде
. Решение данного уравнения ищут в виде ![]() , тогда:
, тогда:
![]() (1.3.1)
(1.3.1)
В предположении, что точка приближения «достаточно близка» к корню ![]() , и что заданная функция непрерывна
, и что заданная функция непрерывна ![]() , окончательная формула для такова:
, окончательная формула для такова:
![]() (1.3.2)
(1.3.2)
С учётом этого функция ![]() определяется выражением
определяется выражением
![]() (1.3.3)
(1.3.3)
Эта функция в окрестности корня осуществляет сжимающее отображение, и алгоритм нахождения численного решения уравнения ![]() сводится к итерационной процедуре вычисления:
сводится к итерационной процедуре вычисления:
![]() (1.3.4)
(1.3.4)
По теореме Банаха последовательность приближений стремится к корню уравнения ![]() .
.

Рисунок 1.1- Графическое представление метода Ньютона
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Достоинства метода Ньютона:
1) если минимизируемая функция является квадратической, то метод позволит найти минимум за один шаг;
2) если минимизируемая функция относится к классу поверхностей вращения, то метод также обеспечивает сходимость за один шаг;
3) если функция несимметрична, то метод не обеспечивает сходимость за конечное число шагов. Но для многих функций достигается гораздо более высокая скорость сходимости, чем при использовании других модификаций метода наискорейшего спуска.
Использование метода Крылова и метода Ньютона приведены в приложениях. Реализация методов производилась в среде МаthСАD и VB.Net.
1.4 Метод Гаусса для решения систем уравнений
Метод Гаусса - классический метод решения системы линейных алгебраических уравнений. Состоит в постепенном понижении порядка системы и исключении неизвестных.
Пусть исходная система выглядит следующим образом
 (1.4.1)
(1.4.1)
Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов)

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ![]() .
.
Тогда переменные ![]() называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число ![]() , где i > r, то рассматриваемая система несовместна.
, где i > r, то рассматриваемая система несовместна.
Пусть, ![]() для любых i > r.
для любых i > r.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ![]()
![]() , где
, где ![]() - номер строки)
- номер строки)
 (1.4.2)
(1.4.2)
где ![]()
Если свободным переменным системы (1.4.2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1.4.1), то по теореме об эквивалентности при элементарных преобразованиях системы (1.4.1) и (1.4.2) эквивалентны, то есть множества их решений совпадают.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получавшуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для: нахождения матрицы, обратной к данной, определения ранга матрицы и численного решения СЛАУ в вычислительной технике
Достоинства метода:
- менее трудоёмкий по сравнению с другими методами.
- позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.
- позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы
приоритетный производственный оптимальный цена продукция
2 ОБОСНОВАНИЕ ВЫБОРА ПРОГРАММНОЙ ПЛАТФОРМЫ
Для выполнения поставленных задач использовались Microsoft Visual Studio 2005 (Visual Basic.Net как язык программирования) и математический пакет MathCAD, для контроля правильности математических расчетов.
Обоснование выбора языка программирования. Классический список проблем, который существовал в программировании, и на разрешение которого было направлено создание корпорацией Microsoft продукта -технологии Microsoft.Net:
- разнообразие частных решений для решения задач разработки крупномасштабного программного обеспечения - как результат, явно ощущалась потребность в разработке некоторого общего подхода, в котором бы критически учитывались все имеющиеся решения, и в рамках которого с единых позиций можно было бы разрешать многие проблемы информационной индустрии;
- сложность интеграции существующих решений в рамках единых программных систем - различие аппаратно-программных платформ, предлагаемых корпоративных решений, вариантность программных компонент выводит проблему интеграции разрабатываемого ПО в число наиболее острых задач программирования;
- трудоемкость разработки распределенных программных систем -возникающие при разработке распределенных систем проблемы обеспечения надежности, безопасности и масштабируемости требовали создания более общих средств решения, определения признаваемых подходов и стандартов;
- широкое распространение Интернет технологий - мир Интернета требовал осмысления накопленных после появления Java решений и ожидал промышленного перехода на технологии сервис-ориентированного программного обеспечения и др.
Платформа Microsolt.Net. для разработки и исполнения программного обеспечения решает эти проблемы программирования.
Платформа .NET состоит из нескольких основных компонентов:
- операционные системы корпорации Microsoft (Windows 2000/ХР/МЕ/СЕ). представляющие собой базовый уровень платформы MS.Net,
- серверы MS.Net (.Net Enterprise Servers) являются программными продуктами корпорации Microsoft, использование которых позволяет снизить сложность разработки сложных программных систем. В числе готовых для применения серверы Application Center 2000, Exchange Server 2000, SQL Server и др.,
- сервисы MS.Net (.Net Building Block Services) представляют собой готовые «строительные блоки» сложных программных систем, которые могут быть использованы через Интернет как сервисные услуги. Набор таких сервисов MS.Net планируется последовательно расширять. Примером имеющегося сервиса платформы MS.Net является Microsoft Passport, позволяющий установить единое имя пользователя и пароль на всех сайтах, поддерживающих аутенфикацию через Passport,
- интегрированная среда разработки приложений Visual Studio.NET (VS.Net) - верхний уровень MS.Net - обеспечивает возможность создания сложного ПО на основе платформы и продолжает в этом плане ряд разрабатываемых корпорацией Microsoft средств разработки профессионального программного обеспечения.
Обоснование выбора математического пакета.
MATHCAD универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета - естественный математический язык, на котором формируются решаемые задачи. Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.
От других продуктов аналогичного назначения, например, Maple & Theorist (компании WaterlooMapleSoftware) и Mathematica (компании WolfResearch), MATHCAD (компании Mathsoft) отличается ориентацией на создание высококачественных документов в режиме WYSIWYG. Это означает, что, внося изменения, пользователь немедленно видит их результаты и в любой момент может распечатать документ во всем блеске. Работа с пакетом за экраном компьютера практически совпадает с работой на бумаге с одной лишь разницей - она более эффективна. Преимущества MATHCAD состоит в том, что он не только позволяет провести необходимые расчеты, но и оформить свою работу с помощью графиков, рисунков, таблиц и математических формул.
3. ОПИСАНИЕ РАЗРАБОТАННЫХ ПРОГРАММНЫХ МОДУЛЕЙ
3.1 Интерфейс пользователя функциональной подсистемы
Для удобства использования программы все основные функции были совмещены на одной главной форме

Главное окно программы для ввода и корректировки исходных данных по технологическим связям, распределении трудовых ресурсов и оценки мнений экспертов на форме предусмотрены групповые фреймы.
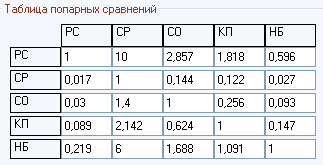
Таблица попарных сравнений

Технологическая матрица

Панель управления программой

При нажатии кнопки «Помощь» на экране появляется окно помощи

Результат работы программы
Кнопки «Расчет приоритетов», «Модель Леонтьева» и кнопка «Определить оптимальную цену» позволяют получить ответы на вопросы:
- оценить математически согласованность таблицы;
- определить приоритеты для производства каждого вида продукции и на основании этих приоритетов рассчитать предварительный режим работы производства;
- оценить является ли производство продуктивным;
- рассчитать максимально возможный столбец выпуска добавочной стоимости;
- для каждого вида продукции рассчитать оптимальную ценовую политику.

Расчет модели Леонтьева
На отдельную форму выносятся графики объемов продаж и прибылей по каждому из товаров


3.2 Анализ полученных результатов
Как описывалось ранее, в рамках данного курсового проекта необходимо было: провести анализ пяти видов продукции и выбрать из них наиболее приоритетные.
По результатам анализа приоритетов был сформирован вектор приоритетов.
Вектор приоритетов
| PC | 0.527 |
| CP | 0.024 |
| СО | 0,073 |
| КП | 0.115 |
| НБ | 0,261 |
На основании этого вектора и производственных возможностей был получен предварительный режим работы предприятия.
Plan1 = 52966,57 Производство рабочих станций 52996 шт
Plan2 = 2123,57 Производство серверов 2123 шт
Plan3 = 7413,2 Производство сетевого оборудования 7413 шт
Plan4 = 11658,14 Производство компьютерной периферии 11658 ш
Plan5 = 25838,51 Производство ноутбуков 25840 шт
Было определено, что производство является продуктивным, т.к. отношение согласованности и индекс согласованности меньше 1. Продуктивность технологической матрицы была подтверждена несколькими способами.
С использование модели Леонтьева определены значения внутреннего потребления и получен столбец конечного и валового продукта.
Таблица внутреннего потребления
| 352.7 | 348 | 263.16 | 689.71 | 374.37 |
| 921,7 | 17,35 | 394.74 | 919.62 | 524.11 |
| 45,18 | 46,37 | 240.27 | 752.42 | 249.58 |
| 120,71 | 78,40 | 552.63 | 318.33 | 582.35 |
| 554,16 | 210,02 | 263.16 | 591.18 | 291.17 |
Конечный выпуск: РС(6349); СР(9387); СО(5526); КП(8277); НБ(5241).
По результатам анализа статистических данных по продажам были определены оптимальные цены по каждому из продуктов.
Рассмотрим принятие решения на примере производства рабочих станций. Принятие решений по другим товарам аналогично.
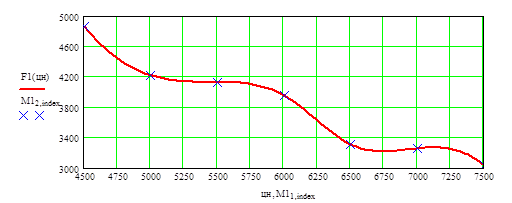
Зависимость объемов продаж от цены на товар

Зависимость прибыли от цены на товар

Определение оптимального уровня цены
Таким образом для продукции №1 оптимальной будет являться цена 4076 грн. за шт.
По СР 9760 грн.
По СО 2779 грн.
По КП 2399 грн.
По НБ 2692 грн.
ВЫВОДЫ
Целью данного курсового проекта являлась разработка системы для оценки перспективности производственных направлений на предприятии. Данная цель была достигнута.
Для достижения поставленной цели были решены следующие задачи:
- оценена математически согласованность таблицы;
- определены приоритеты для производства каждого вида продукции и на основании этих приоритетов рассчитан предварительный режим работы производства;
- оценено является ли производство продуктивным;
- рассчитан максимально возможный столбец выпуска добавочной стоимости;
- для каждого вида продукции рассчитана оптимальная ценовая политика.
Была разработана программа для автоматического расчета показателей работы.
На основании проведенного исследования следует отметить, что наиболее приоритетными являются производство рабочих станций и ноутбуков.
СПИСОК ЛИТЕРАТУРЫ
1. Люстерник Л.А., Соболев В.И. Элементы функционального анализа. - М: Наука, 1965.
2. Канторович Л.В., Акилов Г.П. Функциональный анализ. -М: Наука, 1977г.
3. Лаврентьев М.М. О некоторых некорректных задачах математической физики. - Новосибирск: СО АН СССР, 1962.
4. Саадабаев A.C. Приближенные методы решения нелинейных интегральных и операторных уравнений 1-го рода. - Бишкек, 1997.
5. Саадабаев A.C. Регуляризованный метод Ньютона для решения нелинейного интегрального уравненияпервого рода. Вестник КГНУ. - Бишкек 2001. Сер.З. Выпуск 6. С.59-63.