| Скачать .docx |
Реферат: Метод Дэвидона-Флетчера-Пауэлла
Министерство науки, высшей школы и технической
политики Российской Федерации.
Новосибирский Государственный
Технический Университет.

Реферат по исследованию операций на тему
«Метод Дэвидона - Флетчера - Пауэлла».
Вариант №2.
Факультет: АВТ.
Кафедра: АСУ.
Группа: АС-513.
Студент: Бойко Константин Анатольевич.
Преподаватель: Ренин Сергей Васильевич.
Дата: 19 октября 1997 года.
Новосибирск
Введение.
Первоначально метод был предложен Дэвидоном (Davidon [1959] ), а затем развит Флетчером и Пауэллом (Fletcher, Powell [1963] ). Метод Дэвидона - Флетчера - Пауэлла называют также и методом переменной метрики
. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска задаются в виде -Dj
![]() f(y). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj
, где Dj
- положительно определенная симметрическая матрица порядка n х n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj
+1
представляется в виде суммы Dj
и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два
.
f(y). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj
, где Dj
- положительно определенная симметрическая матрица порядка n х n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj
+1
представляется в виде суммы Dj
и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два
.
Алгоритм Дэвидона - Флетчера - Пауэлла.
Рассмотрим алгоритм Дэвидона - Флетчера - Пауэлла минимизации дифференцируемой функции нескольких переменных. В частности, если функция квадратичная, то, как будет показано позднее, метод вырабатывает сопряженные направления и останавливается после выполнения одной итерации, т.е. после поиска вдоль каждого из сопряженных направлений.
Начальный этап .
Пусть ![]() >0 - константа для остановки. Выбрать точку х1
и начальную симметрическую положительно определенную матрицу D1
. Положить y1
=
x1
, k = j = 1 и перейти к основному этапу.
>0 - константа для остановки. Выбрать точку х1
и начальную симметрическую положительно определенную матрицу D1
. Положить y1
=
x1
, k = j = 1 и перейти к основному этапу.
Основной этап .
Шаг 1.
Если çê![]() f(yj
) çê< e, то остановиться; в противном случае положить dj
= - Dj
f(yj
) çê< e, то остановиться; в противном случае положить dj
= - Dj
![]() f(yj
) и взять в качестве lj
оптимальное решение задачи минимизации f(yj
+ ldj
) при l ³ 0. Положить yj+1
= yj
+ lj
dj
. Если j < n, то перейти к шагу 2. Если j = n, то положить y1
= xk+1
= yn+1
, заменить k на k+1, положить j=1 и повторить шаг 1.
f(yj
) и взять в качестве lj
оптимальное решение задачи минимизации f(yj
+ ldj
) при l ³ 0. Положить yj+1
= yj
+ lj
dj
. Если j < n, то перейти к шагу 2. Если j = n, то положить y1
= xk+1
= yn+1
, заменить k на k+1, положить j=1 и повторить шаг 1.
Шаг 2. Построить Dj +1 следующим образом :
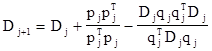 , (1)
, (1)
где
pj = lj dj , (2)
qj
= ![]() f(yj+1
) -
f(yj+1
) - ![]() f(yj
). (3)
f(yj
). (3)
Заменить j на j + 1 и перейти к шагу 1.
Пример.
Рассмотрим следующую задачу :
минимизировать (x1 - 2)4 + (x1 - 2x2 )2 .
Результаты вычислений методом Дэвидона - Флетчера - Пауэлла приведены в таблице 1.
Таблица 1. Результаты вычислений по методу Дэвидона - Флетчера - Пауэлла.
| k |
xk f(xk ) |
j |
yj f(yj ) |
|
çê |
D |
dj |
lj |
yj+1 |
| 1 |
(0.00, 3.00) (52.00) |
1 2 |
(0.00, 3.00) (52.00) (2.70, 1.51) (0.34) |
(-44.00, 24.00) (0.73, 1.28) |
50.12 1.47 |
|
(44.00, -24.00) (-0.67, -1.31) |
0.062 0.22 |
(2.70, 1.51) (2.55, 1.22) |
| 2 |
(2.55, 1.22) (0.1036) |
1 2 |
(2.55, 1.22) (0.1036) (2.45, 1.27) (0.0490) |
(0.89, -0.44) (0.18, 0.36) |
0.99 0.40 |
|
(-0.89, 0.44) (-0.28, -0.25) |
0.11 0.64 |
(2.45, 1.27) (2.27, 1.11) |
| 3 |
(2.27, 1.11) (0.008) |
1 2 |
(2.27, 1.11) (0.008) (2.25, 1.13) (0.004) |
(0.18, -0.20) (0.04, 0.04) |
0.27 0.06 |
|
(-0.18, 0.20) (-0.05, -0.03) |
0.10 2.64 |
(2.25, 1.13) (2.12, 1.05) |
| 4 |
(2.12, 1.05) (0.0005) |
1 2 |
(2.12, 1.05) (0.0005) (2.115, 1.058) (0.0002) |
(0.05, -0.08) (0.004, 0.004) |
0.09 0.006 |
|
(-0.05, 0.08) |
0.10 |
(2.115, 1.058) |
На каждой итерации вектор dj
для j = 1, 2 определяется в виде
–Dj
![]() f(yj
), где D1
– единичная матрица, а D2
вычисляется по формулам (1) - (3). При
f(yj
), где D1
– единичная матрица, а D2
вычисляется по формулам (1) - (3). При
k = 1 имеем p1
= (2.7, -1.49)T
, q1
= (44.73, -22,72)T
. На второй итерации
p1
= (-0.1, 0.05)T
, q1
= (-0.7, 0.8)T
и, наконец, на третьей итерации
p1
= (-0.02, 0.02)T
, q1
= (-0.14, 0.24)T
. Точка yj+1
вычисляется оптимизацией вдоль направления dj
при начальной точке yj
для j = 1, 2. Процедура остановлена в точке
y2
= (2.115, 1.058)T
на четвертой итерации, так как норма çêf(y2
) çê= 0.006 достаточно мала. Траектория движения, полученная методом, показана на рисунке 1.
Рисунок 1. Метод Дэвидона - Флетчера - Пауэлла .
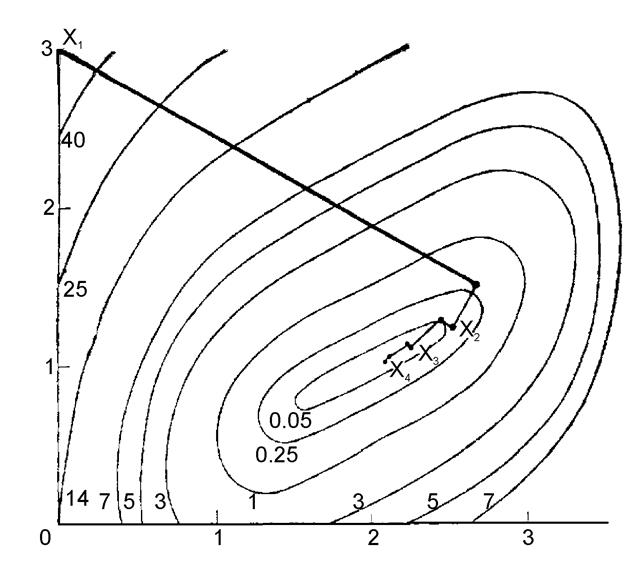
Лемма 1 показывает, что каждая матрица Dj положительно определена и dj является направлением спуска.
Для доказательства леммы нам понадобится :
Теорема 1 . Пусть S - непустое множество в Еn , точка x Î cl S. Конусом возможных направлений в точке x называется множество D = {d : d ¹ 0, x + ld Î S при всех l Î (0, d) для некоторого d > 0}.
Определение. Пусть x и y - векторы из Еn и |xT y| - абсолютное значение скалярного произведения xT y. Тогда выполняется следующее неравенство, называемое неравенством Шварца : |xT y| £ ||x|| ||y||.
Лемма 1.
Пусть y1
Î Еn
, а D1
– начальная положительно определенная симметрическая матрица. Для j = 1, ..., n положим yj+1
= yj
+ lj
dj
, где dj
= –Dj
![]() f(yj
), а lj
является оптимальным решением задачи минимизации f(yj
+ ldj
) при l ³ 0. Пусть, кроме того, для
f(yj
), а lj
является оптимальным решением задачи минимизации f(yj
+ ldj
) при l ³ 0. Пусть, кроме того, для
j = 1, ..., n – 1 матрица Dj+1
определяется по формулам (1) - (3). Если ![]() f(yj
) ¹ 0 для
f(yj
) ¹ 0 для
j = 1, ..., n, то матрицы D1
, ..., Dn
симметрические и положительно определенные, так что d1
, ..., dn
– направления спуска.
Доказательство.
Проведем доказательство по индукции. При j = 1 матрица D1
симметрическая и положительно определенная по условию леммы. Кроме того,
![]() f(y1
)T
d1
= –
f(y1
)T
d1
= –![]() f(y1
)T
D1
f(y1
)T
D1
![]() f(y1
) < 0, так как D1
положительно определена. Тогда по теореме 1 вектор d1
определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j £ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En
, тогда из (1) имеем
f(y1
) < 0, так как D1
положительно определена. Тогда по теореме 1 вектор d1
определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j £ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En
, тогда из (1) имеем
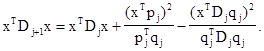 (4)
(4)
Так как Dj
– симметрическая положительно определенная матрица, то существует положительно определенная матрица Dj
1
/2
, такая, что Dj
= Dj
1
/2
Dj
1
/2
. Пусть
a = Dj
1
/2
x и b = Dj
1
/2
qj
. Тогда xT
Dj
x = aT
a, qj
T
Dj
qj
= bT
b и xT
Dj
qj
= aT
b. Подставляя эти выражения в (4), получаем :
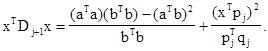 (5)
(5)
По неравенству Шварца имеем (aT a)(bT b) ³ (aT b)2 . Таким образом, чтобы доказать, что xT Dj+1 x ³ 0, достаточно показать, что pj T qj > 0 и bT b > 0. Из (2) и (3) следует, что
pj
T
qj
= lj
dj
T
[![]() f(yj+1
) –
f(yj+1
) – ![]() f(yj
)]. (6)
f(yj
)]. (6)
По предположению![]() f(yj
) ¹ 0, и Dj
положительно определена, так что
f(yj
) ¹ 0, и Dj
положительно определена, так что
![]() f(yj
)T
Dj
f(yj
)T
Dj
![]() f(yj
) > 0. Кроме того, dj
– направление спуска, и, следовательно, lj
> 0. Тогда из (6) следует, что pj
T
qj
> 0. Кроме того, qj
¹ 0, и , следовательно, bT
b= qj
T
Dj
qj
> 0.
f(yj
) > 0. Кроме того, dj
– направление спуска, и, следовательно, lj
> 0. Тогда из (6) следует, что pj
T
qj
> 0. Кроме того, qj
¹ 0, и , следовательно, bT
b= qj
T
Dj
qj
> 0.
Покажем теперь, что xT
Dj+1
x > 0. Предположим, что xT
Dj+1
x = 0. Это возможно только в том случае, если (aT
a)(bT
b) = (aT
b)2
и pj
T
x = 0. Прежде всего заметим, что
(aT
a)(bT
b) = (aT
b)2
только при a = lb, т.е. Dj
1
/2
x = lDj
1
/2
qj
. Таким образом, x = lqj
. Так как x ¹ 0, то l ¹ 0. Далее, 0 = pj
T
x = l pj
T
qj
противоречит тому, что pj
T
qj
> 0 и l ¹ 0. Следовательно, xT
Dj+1
x > 0, т.е. матрица Dj+1
положительно определена.
Поскольку ![]() f(yj
+1
) ¹ 0 и Dj+1
положительно определена, имеем
f(yj
+1
) ¹ 0 и Dj+1
положительно определена, имеем
![]() f(yj
+1
)T
dj+1
= –
f(yj
+1
)T
dj+1
= –![]() f(yj
+1
)T
Dj+1
f(yj
+1
)T
Dj+1
![]() f(yj
+1
) < 0. Отсюда по теореме 1 следует, что dj+1
– направление спуска.
f(yj
+1
) < 0. Отсюда по теореме 1 следует, что dj+1
– направление спуска.
Лемма доказана.
Квадратичный случай.
В дальнейшем нам понадобиться :
Теорема 2.
Пусть f(x) = cT
x + 1 xT
Hx, где Н - симметрическая матрица порядка n x n. Рассмотрим Н - сопряженные векторы d1
, …, dn
и произвольную точку x1
. Пусть lk
для k = 1, …, n - оптимальное решение задачи минимизации
f(xk
+ ldk
) при l Î Е1
и xk+1
= xk
+ ldk
. Тогда для k = 1, …, n справедливы следующие утверждения :
1. ![]() f(xk+1
)T
dj
= 0, j = 1, …, k;
f(xk+1
)T
dj
= 0, j = 1, …, k;
2. ![]() f(x1
)T
dk
=
f(x1
)T
dk
= ![]() f(xk
)T
dk
;
f(xk
)T
dk
;
3. xk+1
является оптимальным решением задачи минимизации f(x) при условии
x - x1
Î L(d1
, …, dk
), где L(d1
, …, dk
) – линейное подпространство, натянутое на векторы d1
, …, dk
, то есть 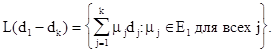 В частности, xn+1
– точка минимума функции f на Еn
.
В частности, xn+1
– точка минимума функции f на Еn
.
Если целевая функция f квадратичная, то в соответствии со сформулированной ниже теоремой 3 направления d1 , …, dn , генерируемые методом Дэвидона - Флетчера - Пауэлла, являются сопряженными. Следовательно, в соответствии с утверждением 3 теоремы 2 метод останавливается после завершения одной итерации в оптимальной точке. Кроме того, матрица Dn+1 , полученная в конце итерации, совпадает с обратной к матрице Гессе Н.
Теорема 3
.
Пусть Н – симметричная положительно определенная матрица порядка n x n. Рассмотрим задачу минимизации f(x) = cT
x + 1 xT
Hx при условии x Î En
. Предположим, что задача решена методом Дэвидона - Флетчера - Пауэлла при начальной точке y1
и начальной положительно определенной матрице D1
. В частности, пусть lj
, j = 1, …, n, – оптимальное решение задачи минимизации f(yj
+ ldj
) при l ³ 0 и yj
+1
= yj
+ lj
dj
, где dj
= -Dj
![]() f(yj
), а Dj
определяется по формулам (1) – (3). Если
f(yj
), а Dj
определяется по формулам (1) – (3). Если ![]() f(yj
) ¹ 0 для всех j, то направления
f(yj
) ¹ 0 для всех j, то направления
d1
, …, dn
являются Н - сопряженными и Dn+1
= H-1
. Кроме того, yn+1
является оптимальным решением задачи.
Доказательство.
Прежде всего покажем, что для j, такого, что 1 £ j £ n, справедливы следующие утверждения :
1. d1 , …, dj линейно независимы.
2. dj T Hdk = 0 для i ¹ k; i, k £ j.
3. Dj+1 Hpk , или, что эквивалентно, Dj+1 Hdk = dk для 1 £ k £ j, pk = lk dk .
Проведем доказательство по индукции. Для j = 1 утверждения 1 и 2 очевидны. Чтобы доказать утверждение 3, заметим прежде всего, что для любого k справедливы равенства
Hpk
= H(lk
dk
) = H(yk+1
- yk
) = ![]() f(yk+1
) –
f(yk+1
) –![]() f(yk
) = qk
. (7)
f(yk
) = qk
. (7)
В частности, Hp1 = q1 . Таким образом, полагая j = 1 в (1), получаем
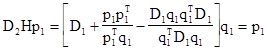 ,
,
т.е. утверждение 3 справедливо при j = 1.
Теперь предположим, что утверждения 1, 2 и 3 справедливы для j £ n – 1. Покажем, что они также справедливы и для j + 1. Напомним, что по утверждению 1 теоремы 2 di
T
![]() f(yj+1
) = 0 для i £ j. По индуктивному предположению di
= Dj+1
Hdi
, i £ j. Таким образом, для i £ j имеем
f(yj+1
) = 0 для i £ j. По индуктивному предположению di
= Dj+1
Hdi
, i £ j. Таким образом, для i £ j имеем
0 = di
T
![]() f(yj+1
) = di
T
HDj+1
f(yj+1
) = di
T
HDj+1
![]() f(yj+1
) = –di
T
Hdj+1
.
f(yj+1
) = –di
T
Hdj+1
.
Ввиду предположения индукции это равенство показывает, что утверждение 2 также справедливо для j+1.
Теперь покажем, что утверждение 3 справедливо для j+1.
Полагая k £ j+1, имеем
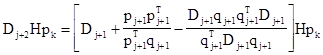 . (8)
. (8)
Учитывая (7) и полагая k = j + 1 в (8), получим, что Dj+2 Hpj+1 = pj+1 . Теперь пусть k £ j. Так как утверждение 2 справедливо для j + 1, то
pj+1 T Hpk = lk lj+1 dj+1 T Hdk = 0. (9)
По предположению индукции из (7) и вследствие того, что утверждение 2 справедливо для j + 1, получаем
![]() . (10)
. (10)
Подставляя (9) и (10) в (8) и учитывая предположение индукции, получаем
![]() .
.
Таким образом, утверждение 3 справедливо для j+1.
Осталось показать, что утверждение 1 справедливо для j+1. Предположим, что ![]() . Умножая это равенство на
. Умножая это равенство на ![]() и учитывая, что утверждение 2 справедливо для j+1, получаем, что
и учитывая, что утверждение 2 справедливо для j+1, получаем, что ![]() . По условию теоремы
. По условию теоремы ![]() , а по лемме 1 матрица
, а по лемме 1 матрица ![]() положительно определена, так что
положительно определена, так что ![]() . Так как H положительно определена, то
. Так как H положительно определена, то ![]() и, следовательно,
и, следовательно, ![]() . Отсюда следует, что
. Отсюда следует, что ![]() , и так как d1
, …, dj
линейно независимы по предположению индукции, то
, и так как d1
, …, dj
линейно независимы по предположению индукции, то ![]() для i = 1, …, j. Таким образом, d1
, …, dj
+1
линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1
, …, dn
следует из утверждений 1 и 2, если положить j = n.
для i = 1, …, j. Таким образом, d1
, …, dj
+1
линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1
, …, dn
следует из утверждений 1 и 2, если положить j = n.
Пусть теперь j = n в утверждении 3. Тогда ![]() для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1
, …, dn
, то
для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1
, …, dn
, то ![]() . Так как D имеет обратную, то
. Так как D имеет обратную, то ![]() , что возможно только в том случае, если
, что возможно только в том случае, если ![]() . Наконец,
. Наконец, ![]() является оптимальным решением по теореме 2.
является оптимальным решением по теореме 2.
Теорема доказана.
Список литературы.
1. Базара М., Шетти К. «Нелинейное программирование. Теория и алгоритмы». М., 1982.
2. Химмельблау Д. «Прикладное нелинейное программирование». М., 1975.