| Скачать .docx |
Реферат: Моделирование систем управления
Южно Уральский Государственный Университет
Кафедра “Автоматики и телемеханики”
К У Р С О В А Я Р А Б О Т А
По теме “Моделирование систем управления”
Вариант № 17
Выполнила: Киселева Е.В.
Группа 421
Проверил: Стародубцев Г.Е.
Миасс, 1999 г.
Задание на курсовое проектирование
1. Провести полный факторный эксперимент вида 3^3 с моделью BLACK BOX
2. Методом регрессионного анализа получить аналитическую зависимость
y=f(x1,x2,t)
3. Составить модель полученного уравнения регрессии.
4. Провести оценку адекватности уравнения регрессии заданной модели по критерию Фишера для a=0,05 , рассчитать среднее абсолютное отклонение координат аналитической модели от заданной.
5. Провести оценку значимости коэффициентов регрессии по критерию Стьюдента для a=0,05
6. Получить графики ошибки
ym -yr =f(t)
ym - выходная координата модели BLACK BOX
yr - выходная координата созданной модели
Значения параметров:
x1= 0.6 ... -1.4
x2= 2.0 ... 0.6
t = 2 ... 10
b = 1.1
Экспериментальные данные.
1. Составим последовательность имитации эксперимента, исходя из данных курсового задания, и представим в матричной форме. Имитационная модель – это модель системы управления с введением случайной переменной погрешности b=1,1.
Необходимо найти аналитическое уравнение связи параметров системы и числовых знаковых коэффициентов. Уравнение регрессии имеет следующий вид:
Y=b0 + S bi xi + S bij xi xj + S bii xi 2
bi xi – линейная регрессия,
bij xi xj - неполная квадратичная регрессия,
bii xi 2 - квадратичная регрессия.
Схема для проведения экспериментов (приложение №1 Vissim 32)
Матричная форма имитационного эксперимента.
| x0 |
x1 |
x2 |
x3=t |
x1*x2 |
x1*x3 |
x2*x3 |
x1*x1 |
x2*x2 |
x3*x3 |
| 1 |
0,6 |
2 |
10 |
1,2 |
6 |
20 |
0,36 |
4 |
100 |
| 1 |
0,6 |
2 |
6 |
1,2 |
3,6 |
12 |
0,36 |
4 |
36 |
| 1 |
0,6 |
2 |
2 |
1,2 |
1,2 |
4 |
0,36 |
4 |
4 |
| 1 |
0,6 |
1,3 |
10 |
0,78 |
6 |
13 |
0,36 |
1,69 |
100 |
| 1 |
0,6 |
1,3 |
6 |
0,78 |
3,6 |
7,8 |
0,36 |
1,69 |
36 |
| 1 |
0,6 |
1,3 |
2 |
0,78 |
1,2 |
2,6 |
0,36 |
1,69 |
4 |
| 1 |
0,6 |
0,6 |
10 |
0,36 |
6 |
6 |
0,36 |
0,36 |
100 |
| 1 |
0,6 |
0,6 |
6 |
0,36 |
3,6 |
3,6 |
0,36 |
0,36 |
36 |
| 1 |
0,6 |
0,6 |
2 |
0,36 |
1,2 |
1,2 |
0,36 |
0,36 |
4 |
| 1 |
-0,4 |
2 |
10 |
-0,8 |
-4 |
20 |
0,16 |
4 |
100 |
| 1 |
-0,4 |
2 |
6 |
-0,8 |
-2,4 |
12 |
0,16 |
4 |
36 |
| 1 |
-0,4 |
2 |
2 |
-0,8 |
-0,8 |
4 |
0,16 |
4 |
4 |
| 1 |
-0,4 |
1,3 |
10 |
-0,52 |
-4 |
13 |
0,16 |
1,69 |
100 |
| 1 |
-0,4 |
1,3 |
6 |
-0,52 |
-2,4 |
7,8 |
0,16 |
1,69 |
36 |
| 1 |
-0,4 |
1,3 |
2 |
-0,52 |
-0,8 |
2,6 |
0,16 |
1,69 |
4 |
| 1 |
-0,4 |
0,6 |
10 |
-0,24 |
-4 |
6 |
0,16 |
0,36 |
100 |
| 1 |
-0,4 |
0,6 |
6 |
-0,24 |
-2,4 |
3,6 |
0,16 |
0,36 |
36 |
| 1 |
-0,4 |
0,6 |
2 |
-0,24 |
-0,8 |
1,2 |
0,16 |
0,36 |
4 |
| 1 |
-1,4 |
2 |
10 |
-2,8 |
-14 |
20 |
1,96 |
4 |
100 |
| 1 |
-1,4 |
2 |
6 |
-2,8 |
-8,4 |
12 |
1,96 |
4 |
36 |
| 1 |
-1,4 |
2 |
2 |
-2,8 |
-2,8 |
4 |
1,96 |
4 |
4 |
| 1 |
-1,4 |
1,3 |
10 |
-1,82 |
-14 |
13 |
1,96 |
1,69 |
100 |
| 1 |
-1,4 |
1,3 |
6 |
-1,82 |
-8,4 |
7,8 |
1,96 |
1,69 |
36 |
| 1 |
-1,4 |
1,3 |
2 |
-1,82 |
-2,8 |
2,6 |
1,96 |
1,69 |
4 |
| 1 |
-1,4 |
0,6 |
10 |
-0,84 |
-14 |
6 |
1,96 |
0,36 |
100 |
| 1 |
-1,4 |
0,6 |
6 |
-0,84 |
-8,4 |
3,6 |
1,96 |
0,36 |
36 |
| 1 |
-1,4 |
0,6 |
2 |
-0,84 |
-2,8 |
1,2 |
1,96 |
0,36 |
4 |
Матрица значений полученных в результате эксперимента.
| y0 |
y1 |
y2 |
y3 |
y4 |
Ysr |
| 235,09 |
235,41 |
235,727 |
234,95 |
236,37 |
235,51 |
| 134,71 |
136,34 |
136,881 |
135,22 |
135,76 |
135,78 |
| 67,067 |
68,544 |
67,82 |
68,197 |
68,574 |
68,04 |
| 140,38 |
140,7 |
141,017 |
140,24 |
141,66 |
140,8 |
| 60,996 |
62,634 |
63,171 |
61,508 |
62,046 |
62,071 |
| 14,357 |
15,834 |
15,11 |
15,487 |
15,864 |
15,33 |
| 64,287 |
64,606 |
64,926 |
64,146 |
65,565 |
64,706 |
| 5,906 |
7,544 |
8,081 |
6,418 |
6,956 |
6,981 |
| -19,73 |
-18,26 |
-18,979 |
-18,6 |
-18,23 |
-18,759 |
| 100,25 |
100,57 |
100,887 |
100,11 |
101,53 |
100,67 |
| 65,866 |
67,504 |
68,041 |
66,378 |
66,916 |
66,941 |
| 64,227 |
65,704 |
64,98 |
65,357 |
65,734 |
65,2 |
| -9,162 |
-8,843 |
-8,523 |
-9,303 |
-7,884 |
-8,743 |
| -22,54 |
-20,91 |
-20,368 |
-22,03 |
-21,49 |
-21,468 |
| -3,182 |
-1,705 |
-2,429 |
-2,052 |
-1,675 |
-2,2086 |
| -99,95 |
-99,63 |
-99,313 |
-100,1 |
-98,67 |
-99,533 |
| -92,33 |
-90,7 |
-90,158 |
-91,82 |
-91,28 |
-91,258 |
| -51,97 |
-50,5 |
-51,219 |
-50,84 |
-50,47 |
-50,999 |
| -53,19 |
-52,87 |
-52,553 |
-53,33 |
-51,91 |
-52,773 |
| -21,57 |
-19,94 |
-19,398 |
-21,06 |
-20,52 |
-20,498 |
| 42,787 |
44,264 |
43,54 |
43,917 |
44,294 |
43,76 |
| -177,3 |
-177 |
-178,663 |
-177,4 |
-176 |
-177,28 |
| -124,7 |
-123 |
-122,509 |
-124,2 |
-123,6 |
-123,61 |
| -39,32 |
-37,85 |
-38,569 |
-38,19 |
-37,82 |
-38,349 |
| -282,8 |
-282,5 |
-282,153 |
-282,9 |
-281,5 |
-282,37 |
| -209,2 |
-207,5 |
-206,999 |
-208,7 |
-208,1 |
-208,1 |
| -102,8 |
-101,3 |
-102,059 |
-101,7 |
-101,3 |
-101,84 |
Вычислим коэффициенты B по формуле
B=(XT X)-1 XT Ysr
XT – транспонированная матрица
Ysr- средние экспериментальные значения
| b0 |
-29,799251 |
| b1 |
13,6541852 |
| b2 |
9,96405181 |
| b3 |
-15,946707 |
| b4 |
-21,000048 |
| b5 |
16,508325 |
| b6 |
7,50010119 |
| b7 |
-9,3224778 |
| b8 |
19,0904535 |
| b9 |
0,99813056 |
Вычисления производились в Microsoft Excel по следующей формуле
=МУМНОЖ(МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП (Хматрица);Хматрица));ТРАНСП(Хматрица)); Y матрица)
Полученные коэффициенты подставим в уравнение регрессии и построим схему для проведения эксперимента (приложение №2,3 Vissim 32) и проведем эксперимент без использования дельты или шума.
Внесем полученные данные в столбец (Yip) таблицы.
| Ysr |
Si кв |
Yip |
(Yi-Yip)2 |
| 235,51 |
0,3219 |
234,7 |
0,61090 |
| 135,78 |
0,7492 |
135,5 |
0,06574 |
| 68,04 |
0,3897 |
68 |
0,00163 |
| 140,8 |
0,3219 |
140 |
0,68327 |
| 62,071 |
0,75 |
61,77 |
0,09060 |
| 15,33 |
0,3897 |
15,25 |
0,00646 |
| 64,706 |
0,3214 |
63,93 |
0,60218 |
| 6,981 |
0,75 |
6,73 |
0,06300 |
| -18,759 |
0,3897 |
-18,78 |
0,00046 |
| 100,67 |
0,3219 |
99,93 |
0,54258 |
| 66,941 |
0,75 |
66,73 |
0,04452 |
| 65,2 |
0,3897 |
65,21 |
0,00009 |
| -8,743 |
0,3214 |
-9,51 |
0,58829 |
| -21,468 |
0,75 |
-21,71 |
0,05856 |
| -2,2086 |
0,3897 |
-2,23 |
0,00046 |
| -99,533 |
0,3216 |
-100,3 |
0,51380 |
| -91,258 |
0,75 |
-91,45 |
0,03686 |
| -50,999 |
0,3897 |
-50,97 |
0,00082 |
| -52,773 |
0,3214 |
-53,48 |
0,49985 |
| -20,498 |
0,75 |
-20,68 |
0,03312 |
| 43,76 |
0,3897 |
43,79 |
0,00088 |
| -177,28 |
0,9015 |
-177,6 |
0,12013 |
| -123,61 |
0,7492 |
-123,8 |
0,04902 |
| -38,349 |
0,3897 |
-38,35 |
0,00000 |
| -282,37 |
0,3219 |
-283,1 |
0,48525 |
| -208,1 |
0,7492 |
-208,3 |
0,02938 |
| -101,84 |
0,3892 |
-101,8 |
0,00240 |
| S Si=13,73 |
S = 5,13026 |
||
Так как результаты опытов обладают статической неопределенностью, поэтому опыты воспроизводим несколько раз при одних и тех же значениях факторов для повышения точности коэффициентов регрессии за счет эффекта понижения дисперсии.
n=27 - экспериментов
m=10 – количество членов уравнения
Si 2 =1/g-1 * S (Ygi -Yi )2 , g - количество экспериментов ( 5)
Sy 2 =1/n * S Si 2
S0 = å (Yi -Yip )2 /n-m – среднеквадратичная ошибка на степень свободы
d = å |Yi -Yip |/n – среднее обсолютное отклонение между расчетными значениями
Адекватность вида регрессии уравнения определяется по критерию Фишера, а значимость коэффициентов по критерию Стьюдента и доверительного интервала на его основе.
F расч = S0 2 /Sy2 < F табл ( a , n-m)
F табл = 1 , 77 ,
a =0,05 – уровень значимости
1- a ® р – вероятность с которой уравнение будет адекватно.
n-m Þ 27-10=17 – число степеней свободы
S D bj 2 =Sy 2 /n - дисперсия коэффициентов взаимодействия
D bj = ± tc * Ö Sy 2 / Ö n
tc =2,12
| Sy2 |
0,5085 |
Fрасч . |
1,08031201 |
| So |
0,5493 |
S g 2 |
0,01883355 |
| d |
0,4359 |
D bj |
0,29093901 |
| p |
0,95 |
F табл = 1 , 75 > Fрасч .= 1,08, значит система адекватна.
Уравнение регрессии примет вид.
Y=-29,79+13,65x1 +9,96x2 -15,94x3 -21x1 x2 +16,5x1 x3 +7,5x2 x3 -9,32x1 2 +19,09x2 2 +0,99x3 2
График ошибки (см. приложение № 4).
Вывод.
Исходя из полученных значений сделаем вывод, что полученная система очень мало отличается от заданной.
Уравнения адекватны
Коэффициенты значимы
Приложение № 1
 |
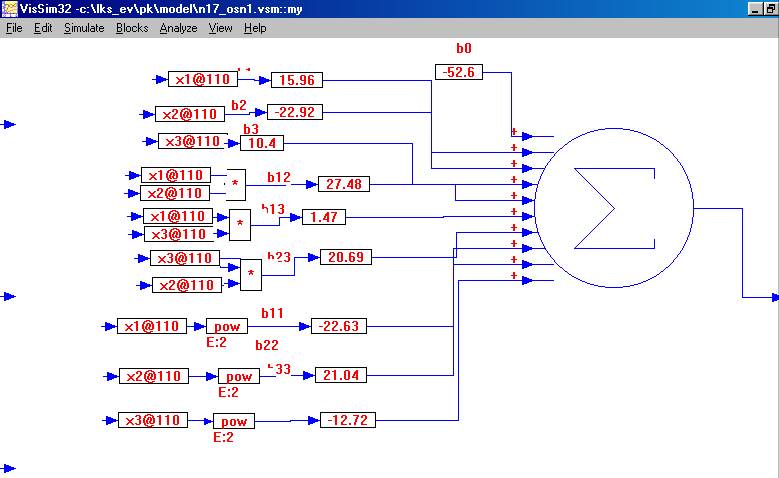
Приложение № 2
 |