| Скачать .docx |
Курсовая работа: Технология сборки и испытания летательных аппаратов
Министерство образования РФ
МАТИ – Российский государственный технологический Университет им. К.Э.Циолковского
Кафедра «Технология производства
приборов и систем управления летальных аппаратов»
Пояснительная записка
к курсовому проекту по курсу
« Технология сборки и испытания летательных аппаратов»
на тему « Разработка оборудования для ультрачистой промывки двигателей аэрокосмического приборостроения»
Результаты смотров Студент гр. ЗАСУ - 5 - 60
К.В.Муллахметов
1 смотр %
Руководитель
2 смотр % доц.к.т.н.
Е.Г.Чуреев
3 смотр %
Проверил
проф., к.т.н.
В.И.Молодницкий
Москва 2004 г.
Оглавление
1. Исследование и выбор оптимальных характеристик светогидравлической
системы (СГС) для ультрачистой промывки деталей приборостроения . . . . . . . . . . . .3.
1.1. Выбор основных фактов, оказывающих влияние на процесс светогидравлической промывки . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . 3.
1.2. Систематическое планирование эксперимента при исследовании
оптимальных характеристик СГС . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.
1.3. Определение оптимальных условий светогидравлической
промывки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13.
2. Разработка структурной схемы установки для светогидравлической
промывки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17.
2.1. Структурная схема установки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17.
3. Расчет оптического тракта установки для промывки . . . . . . . . . . . . . . . . . . . . . . . . . . 23.
4. Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25.
5. Спецификация на установку . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30.
1. Исследование и выбор оптимальных характеристик светогидравлической системы (СГС) для ультрачистой промывки деталей приборостроения.
1.1. Выбор Основных факторов оказывающих влияние на процесс светогидравлической промывки.
Светогидравлическая система должна состоять из целого ряда элементов, причем, кждый из этих элементов в той или иной степени оказывает влияние на процесс взаимодействия луча лазера с очищающей жидкостью.
Важнейшими элементами структуры СГС являются: лазер; среды, передающие световой поток (воздушная, оптическая система и жидкая) и парожидкостная область очищающей жидкости, поглощающая излученный лазером свет. В свою очередь, параметры каждого из перечисленных элементов структуры СГС зависят от первичных технологических факторов.
Качественно и количественно оценить вклад рассмотренных факторов в процесс промывки заготовок при светогидравлической обработке можно лишь используя метод многофакторного регрессивного анализа.
Этот метод позволяет представить математическую модель любого реального технологического процесса по зависимостям, связывающим значения выходной величины со значениями параметров, заданными на выходе.
В качестве выходной величины были приняты параметры схлопывания парожидкостной области за счет развития светогидравлического эффекта и оцениемой количеством парожидкостных областей образованных после взаимодействия с лучом лазера (параметр К)
Правомерность такого выбора в качестве выходной величины определяется требованиями математической корректности, а именно тем, что эта величина является: эффективной с точки зрения достижения заданной технологической цели; количественной величиной, выражающейся числом; статически эффективной, то есть имеющей физический смысл при всех значениях входных параметров; достаточно легко определяемой; существующей при всех значениях входных параметров, то есть выполняются все необходимые и достаточные условия для выбора входной величины.
Анализ входных параметров (основных технологических факторов светогидравлической промывки) показывает, что все факторы можно условно разделить на три группы. А именно: к первой группе отнести факторы, которые могут изменить свои параметры в широких пределах в зависимости от тех или иных условий взаимодействия света с каплей промывочной жидкости; ко второй – факторы, которые должны быть согласованы с другими факторами СГС; и, наконец, к третьей группе отнести факторы, которые могут оставаться постоянными для выбранной схемы взаимодействия в СГС.
К первой группе, согласно принятой классификации, можно отнести следующие факторы:
WΣ ; r; Пк (3 фактора),
где: WΣ – энергетические параметры лазера;
ч –радиус парожидкостной области;
Пк – показатель преломления парожидкостной области;
- ко второй группе – факторы:
λ; Пв.с; Ув.с; Уж.с.; Пж.с.; Ук; Zк; Уо.с; По.с; Zо.с; ∆F; (11 факторов)
где: λ – длина волны лазера;
Пв.с – преломление воздушной среды;
Ув.с – коэффициент рассеивания воздушной среды;
Уж.с – коэффициент рассеивания жидкой среды;
Пж.с – преломление жидкой среды;
Ук – коэффициент рассеивания капли промывочной жидкости;
Zк – коэффициент преломления капли промывочной жидкости;
Уо.с. – коэффициент рассеивания оптической системы;
По.с. – преломление оптической системы
- к третьей группе – факторы:
τимп; Ө; t, Авозд.; Аос; Zжс; m; ∆F; Аж.с.; Кт.ф. (10 факторов).
где: τимп – длительность импульса лазера;
Ө - угол расходимости луча лазера;
t – количество импульсов лазера;
Авозд – протяженность воздушного промежутка;
Аос – протяженность оптической системы;
Zжс – коэффициент преломления жидкой среды;
m – масса капли промывочной жидкости;
∆F – положение фокуса оптической системы относительно капли промывочной жидкости;
Аж.с. – протяженность жидкой среды;
Кт.ф. – теплофизические параметры капли промывочной жидкости.
Таким образом, из большого разнообразия 24 основных технологических факторов оказывающих влияние на процесс светогидравлического эффекта, при проведении многофакторного регрессивного анализа можно не учитывать влияние 10 факторов, отнесенных к третьей группе. Так как можно условно принять, что эти факторы остаются постоянными для выбранной схемы взаимодействия и не изменяют свое значение не только в течение всего времени протекания светогидравлического эффекта, но и в течение более длительного времени.
Анализ факторов, представленных во второй группе, показывает, что фактор λ (длина волны лазера) который должен быть согласован с длиной волны цвета капли промывочной жидкости, является величиной постоянной для выбранного лазера, так как изменить этот параметр в лазере типа ЛТИ-ПЧ не представляется возможным. Легче всего управлять этим фактором, изменяя цвет капли промывочной жидкости, то есть воздействовать на фактор Пк (показатель преломления парожидкостной области), отнесенный к первой группе факторов.
Факторы Пв.с; Ув.с; Уж.с.; Пж.с.; Ук; Zк; Уо.с; По.с; Zо.с, то есть параметры, учитывающие поглощающие, отражательные и рассеивающие способности различных элементов структуры СГС, так же можно условно отнести к постоянным. Не изменяющим свое значение в течение всего времени процесса взаимодействия, но изменяющим свои параметры в течение более длительного времени.
Фактор ∆F (положение точки фокуса оптической системы относительно поверхности капли), отнесенного ко второй группе факторов, так же можно считать постоянным, так как в ряде работ [1; 5; 8] было показано, что световой поток, образованный лазером в жидкой среде, изменяет свои геометрические параметры, образуя протяженный световой цилиндр. Длина этого цилиндра составляет 11,95 мм (для воды) при максимальном диаметре сферической капли промывочной жидкости (фреон) равного 6,5 мм. Следовательно, протяженность минимального диаметра светового цилиндра почти в два раза больше диметра сферической капли и, таким образом, нет необходимости точно учитывать положение точки фокуса относительно поверхности капли, то есть правомочно утверждение о том, что указанный фактор можно считать постоянным.
Таким образом, из всего ряда перечисленных технологических факторов, можно выделить основные факторы, в наибольшей степени оказывающие влияние на параметры выходных величин, это: энергия светового импульса (WΣ ), диаметр сферы капли промывочной жидкости (2r) и поглощающая способность капли (Пк).
Таким образом, основной задачей является проведение многофакторного эксперимента и получение по его данным зависимости:
К= t(WΣ ; r; Пк)
а также оценка влияния и вклада каждого фактора из указанных в отдельности и во взаимосвязи на величину выходного параметра в камере светогидравлической промывочной установки.
1.2. Статистическое планирование эксперимента при исследовании оптимальных характеристик СГС .
С целью упрощения нахождения оптимальных характеристик СГС рационально применять методы статистического планирования эксперимента, позволяющие находить оптимум с помощью сравнительно небольшого количества экспериментов.
Одним из наиболее пригодных для данного случая методов является метод полного многофакторного планирования.
Как известно [25], постановка полного факторного эксперимента сводится к следующим операциям: выбору уравнения регрессии, составлению плана полного факторного эксперимента, расчету коэффициентов регрессии, оценке значимости этих коэффициентов и анализу уравнения регрессии, после этого можно переходить к поиску оптимума.
Априорно устанавливаем, что условия протекания процесса в камере светогидравлической промывочной установки не оптимальные, поэтому функция выхода может быть с достаточной точностью описана степенным рядом, не содержащим переменных во второй и выше степенях.
Уравнение регрессии тогда запишется в виде:
i ij
г = βo + Σ βi xi + Σij xi xj
(1.2)
В результате экспериментов нельзя абсолютно точно определить значения теоретических коэффициентов регрессии βo; βi ;βij , можно лишь вычислить значения выборочных коэффициентов βo; βi ;βij , связанных с теоретическими соотношениями:
βi = βi ± ΣS
βij = βij ± ΣS
βo = βo ± Σβii + Σβiii … ΣS
(1.3)
где ΣS – ошибка, связанная с наличием неучтенных факторов и погрешностью метода.
Таким образом, уравнение регрессии, полученное на основании эксперимента, имеет вид:
ŷ =bo + Σbi xi bij xi xj
(1.4)
Для трех выбранных факторов, в соответствии с формулой (1.4) уравнение регрессии принимает вид:
ŷ = bo +b1 x1 + b2 x2 +b3 x3 +b12 x1 x2 +b13 x1 x3 + b23 x23 +b123 x1 x2 x3
(1.5)
Здесьx1 x2 – значения факторов, bo – свободный член, равный выходу при нулевых условиях (то есть при х = 0), b1 ;b2 – коэффициенты регрессии соответствующих факторов, указывающие на влияние того или иного фактора на изучаемый процесс; b123 - коэффициент регрессии при произведении факторов, свидетельствующий о наличии взаимодействия между факторами.
Реально действующие факторы заменим на формализованные. С этой целью фактор WΣ (энергия светового импульса) обозначим х1 ; фактор 2r (диаметр сферы жидкого катализатора) – через х2 ; фактор Пк (поглощающая способность капли) – через х3 .
Выходные величины – факторы, участвующие в эксперименте, не подвергались конфлюэнтному анализу, так как параметр х1 мог задаваться с точностью +-0,5% (указанная величина соответствует точности задания энергии светового импульса по техническому паспорту на лазер ЛТИ-ПЧ и экспериментальной проверке указанных данных); параметра х2 - с точностью 0,1% (что соответствует точности задания диаметра капли промывочной жидкости); параметр х3 – с точностью 0,01‰ (соответствует точностям определения и поглощающим способностям капли). Кроме этого они совместимы в любых сочетаниях, между ними отсутствует корреляция. Они однозначны и управляемы, то есть выполняются все необходимые и достаточные требования математической корректности к принятой совокупности факторов.
Для каждого из выбранных факторов устанавливается условный нулевой уровень 0xi , назначаемый на основании опытных или теоретических данных, а при отсутствии таковых – произвольно. Для тех же факторов выбираются единицы варьирования λi , на которые меняются условия по каждому фактору в сторону уменьшения или увеличения его от нулевого уровня.
Выбор единиц варьирования является весьма ответственным этапом, так как при слишком малых единицах варьирования каких либо факторов может оказаться, что эффект от их действия незначим не потому, что они не оказывают влияния на процесс, а потому, что этот эффект ниже ошибки метода измерения выхода. С другой стороны, при слишком больших единицах варьирования может оказаться, что исследуемая поверхность отклика не может быть описана уравнением, не содержащим членов высших степеней.
Выбор параметров 0xi и λi для указанных трех факторов основывается на том, что для первого фактора (WΣ ) минимальное значение параметра световой энергии составляет 0,1 мВт, что близко к нижнему порогу световой накачки для применяемого лазера ЛТИ-ПУ, а максимальное значение – 0,3 мВт, что соответствует верхнему порогу световой накачки. Для второго фактора (2r) минимальное значение диаметра капли промывочной жидкости условно было выбрано 0,2 мкм, а максимальное – равным 0,6 мкм, что соответствует условию отрыва капли от патрубка и всплытию ее на поверхность жидкой среды.
Для третьего фактора (Пк) минимальное значение коэффициента преломления выбрано равным 2%, максимальное – равным 5%, что близко к значениям, указанным в справочниках на физические параметры очищающей жидкости.
Составим матрицу планирования, исходя из того, чтобы в данном эксперименте были исчерпаны все возможные комбинации варьируемых факторов на верхнем и нижнем уровнях. Необходимое число вариантов Nв = 2i .
где i – количество исследуемых факторов.
В рассматриваемом случае Nв = 23 = 8. Для оценки значимости коэффициентов регрессии будем производить каждый опыт три раза (Кn = 3).
Тогда матрица планирования будет иметь вид: Таблица 1.
| Фактор | 0 х i | i | + I | - I | Размерность |
| W (X1) | 0.200 | 0.100 | 0.300 | 0.100 | Джоули |
| 2r (X2) | 0.1 | 0.4 | 0.2 | 0.2 | мм |
| Пк (Х3) | 5 | 3 | 8 | 2 | % |
Таблица 2.
| № - | Планирование | Расчет | Выход (мм) Н | |||||||||
| варианта | Х0 | Х1 | X2 | X3 | X1X2 | X1X3 | X2X3 | X1X2X3 | Уn I | Уn II | Уn III |
Уn |
| 1 | + | - | - | - | + | + | + | - | ||||
| 2 | + | + | - | + | - | + | - | - | ||||
| 3 | + | - | - | + | + | - | - | + | ||||
| 4 | + | + | - | - | - | - | + | + | ||||
| 5 | + | - | + | + | - | - | + | - | ||||
| 6 | + | + | + | - | + | - | - | - | ||||
| 7 | + | - | + | - | - | + | - | + | ||||
| 8 | + | - | + | + | + | + | + | + | ||||
Коэффи- циент регрессии |
b0 | b1 | b2 | b3 | b12 | b13 | b23 | b123 | -- | -- | -- | 88.14 |
| 11.01 | 3.18 | 2.02 | -0.18 | -0.05 | -0.04 | -0.57 | -0.057 | -- | -- | -- |
Σ Уn |
|
![]() Кроме указанных экспериментов для последующей оценки линейности уравнения регрессии был 4 раза определен выход на нулевом уровне. Значения уо составили: 10,65; 10,82; 10,95 и 10,72, откуда среднее значение выхода уо = 10,78
Кроме указанных экспериментов для последующей оценки линейности уравнения регрессии был 4 раза определен выход на нулевом уровне. Значения уо составили: 10,65; 10,82; 10,95 и 10,72, откуда среднее значение выхода уо = 10,78
Рассчитываем коэффициент регрессии:
Таблица 3.
1 Nb _ _
No |
bo = 11.01 |
1 Nb __
No |
b1 = 3.18 b2 = 2.02 b3 = - 0.18 |
1 Nb __
No |
b12 = - 0.05 b13 = - 0.04 b23 = - 0.057 b123 = - 0.075 |
Уравнение регрессии тогда примет вид:
У = 11,01 + 3,18х1 + 2,02х2 – 0,18х3 – 0,05x12 – 0.04x13 – 0.057x23 – 0.075x123
(1.6)
Это уравнение может являться математической моделью процесса, однако, прежде необходимо определить значимость входящих в него коэффициентов регрессии.
С этой целью необходимо найти выборочную дисперсию. Для этого вычисляются:
1) построчная дисперсия
![]()
![]() ∑(yN
– yN
k
)2
∑(yN
– yN
k
)2
![]() S2
(yN
k
) =
S2
(yN
k
) =
k – 1
S1 2 (yN k ) = 0.0043
S2 2 (yN k ) = 0.0072
S3 2 (yN k ) = 0.01
S4 2 (yN k ) = 0.0016
S5 2 (yN k ) = 0.0046
S6 2 (yN k ) = 0.0109
S7 2 (yN k ) = 0.0092
S8 2 (yN k ) = 0.0156
2) дисперсия воспроизводимости:
∑ S2 ( yN k )
![]() S2
(y) = = 0,0634 / 8 = 0,0079
S2
(y) = = 0,0634 / 8 = 0,0079
Nb
(1.8)
3) дисперсия среднего значения:
∑ S2 ( yN k )
![]() S2
(y) = = 0.0079 / 3 = 0,0026
S2
(y) = = 0.0079 / 3 = 0,0026
kn (1.9)
4) дисперсия коэффициентов регрессии:
∑ S2 ( yN k )
![]() S2
(y) = = 0,0026 / 8 = 0,0003
S2
(y) = = 0,0026 / 8 = 0,0003
Nb
(1.10)
по которой находится ошибка коэффициентов регрессии:
S (bi) = √S2 (bi) = 0.017
Для оценки значимости коэффициентов регрессии составим неравенство:
Bi > S (bi) tp (f)
(1.11)
где S (bi) – ошибка коэффициента регрессии, а
tp (f) – коэффициент Стьюдента, находимый по таблицам для требуемой достоверности и числа степеней свободы f, с которыми были определены коэффициенты регрессии. Для рассматриваемой задачи f = 8 * 2 = 16 и t95 (16) = 2,12. Тогда S(bi)t95 (16) = 0.017*1.12 = 0.36, f = Nb * (kn – 1)
Отсюда :
b0 = 11,01 > 0,36 – значимый коэффициент регрессии
b1 = 3,18 > 0,36 – значимый коэффициент регрессии
b2 = 2,02 > 0,36 – значимый коэффициент регрессии
b3 = 0,18 < 0,36 – незначимый коэффициент регрессии.
Рассматриваемый коэффициент регрессии b3 может быть незначимым по многим причинам, в частности:
- выбрана слишком маленькая единица варьирования для данного фактора, а ошибка метода велика;
- нулевой уровень по данному фактору лежит уже в оптимуме и, следовательно, изменение данного фактора на величину может не вызывать изменения выхода;
- и, наконец, данный фактора действительно не оказывает никакого влияния на процесс, так как не имеет к нему отношения.
В рассматриваемом случае нулевой уровень по третьему фактору лежит в оптимуме, а потому он и не вызывает изменения выхода.
Кроме этого, знак минус при третьем факторе свидетельствует о том, что с увеличением показателя преломления уменьшается выход. Это происходит по всей видимости потому, что поглощающая способность капли увеличивается до определенной величины, затем отражающая способность его становится доминирующей, то есть капля выполняет роль своеобразного зеркала на пути светового потока лазера.
Коэффициенты Х1; Х2; Х23; Х123 незначимы для Р = 95%, а потому уравнение регрессии (1.5) после отбрасывания незначимых членов будет иметь вид:
ŷ = 11,01 + 3,15х1 + 2,02х2 – 0,18х3
(1.12)
проанализируем уравнение регрессии (1.12) с точки зрения проверки правильности выбранной гипотезы, что система линейна, иными словами необходимо установить, может ли выход процесса быть описан уравнением без членов высших порядков и, возможно, без членов, учитывающих парные взаимодействия.
Оценим значимость коэффициентов регрессии при членах высших порядков.
Для этого был проведен эксперимент в нулевой точке с числом повторностей Z = 4.
__
Вычисленное среднее значение Уо является чистой оценкой для УоZ ,
iiii
а разность (Уо – bo) = [β – (βo + ∑ βii )] = ∑ βii оценкой для суммы коэффициентов регрессии при членах высших порядков. Если она незначима, то принятое предположение о возможности описания процесса уравнением без квадратичных и более членов правильно.
![]()
![]() Для оценки значимости, зная bo и S2
(bo) = S2
(bi), можно воспользоваться формулой (1.13):
Для оценки значимости, зная bo и S2
(bo) = S2
(bi), можно воспользоваться формулой (1.13):
_ S2 √ (Nb + Z)
![]()
![]() [Уо - bo] >
[Уо - bo] >
Nb * Z * tp (f)
(1.13)
![]() где _ (Nb – 1) S2
(bi) + (Z – 1) S2
(Уо)
где _ (Nb – 1) S2
(bi) + (Z – 1) S2
(Уо)
![]() S2
=
S2
=
Nb + Z – 2
среднее взвешенное из двух дисперсий. Здесь в добавление к ранее принятым обозначениям tp (f) –значение коэффициента Стьюдента, находимое по таблице, для выбранного уровня доверительной вероятности и числа степеней свободы.
![]() Для рассматриваемой задачи:
Для рассматриваемой задачи:
![]() (Уо – bо) = │10,78 – 11,01│= 0,23
(Уо – bо) = │10,78 – 11,01│= 0,23
Расчет S2 (Уо) ведется по формуле:
_
S2 (Уо) = ∑│Уо - УоZ │/ Z (Z – 1) = 0,425
(1.14)
где Z – число повторностей в определении У.
Тогда S2 = 0,23 < 0,46
Различие между Уо и bо статически незначимо, следовательно, гипотеза о возможности использования уравнения без квадратичных членов верна.
Теперь для упрощения математической модели, проверим возможность описания процесса линейным уравнением, то есть уравнением без парных членов. Для этого оставим дополнительную матрицу планирования по следующей схеме (Табл. 4).
Из этой матрицы вычислим дисперсию неадекватности данной модели (без парных взаимодействий):
∑(УN –УN )2
S2 ag = —————— = 21,61 / 7 = 3,08
N + l – i – 1
Здесь N + l – i – 1 – число отброшенных членов, где:
l – число исключенных парных взаимодействий. Теперь сравним S2 ag с дисперсией воспроизводимости, рассчитанной выше, по критерию Фишера (F):
Fрасч = S2 ag / S (У)2 = 18,117
№ вари анта |
Х1 |
Х2 |
Х3 |
УN |
УN =bo+b1+и2Х2+и3Х3 |
|
|
| 1 | - | - | - | 7.3 | У1 = 5.99 | 1.39 | 1.39 |
| 2 | + | - | + | 13.83 | У2 = 11.59 | 2.24 | 5.01 |
| 3 | - | - | + | 7.04 | У3 = 5.63 | 1.41 | 1.98 |
| 4 | + | - | - | 14.01 | У4 = 12.35 | 1.66 | 2.75 |
| 5 | - | + | + | 8.08 | У5 = 9.67 | 1.59 | 2.52 |
| 6 | + | + | + | 15.08 | У6 = 16.39 | 1.31 | 1.71 |
| 7 | - | + | - | 8.33 | У7 = 10.03 | 1.7 | 2.89 |
| 8 | + | + | + | 14.35 | У8 = 16.03 | 1.68 | 2.82 |
Коэффициент регрессии |
bo = 11.01 | _ ∑(УN – ŷN )2 = 21.61 |
|||||
| b1 = 3.18 | |||||||
| b2 = 2.02 | |||||||
| b3 = - 0.18 | |||||||
Критерий Фишера, найденный по таблице 4 F (f1 ;f2 ) для степеней свободы f1 = N + l – i – 1 = 7 и f2 = Кп – 1 = 3 – 1 = 2 - числа степеней свободы, для которого определялась дисперсия воспроизводимости, равняется для вероятности 95%
F95 (7;2) = 19,35, а для вероятности 99%
F95 (7;2) = 99,36. Таким образом,
Fрасч ≤ F (f1 ;f2 ) и, следовательно, можно отбросить парные взаимодействия и пользоваться линейной моделью.
Итак, теперь с достаточной точностью можно утверждать, что процесс описывается следующей математической моделью:
Ŷ = bo + b1 x1 + b2 x2 b3 x3 = 11,01 + 3,18х1 +2,02х2 – 0,18х3
1.3. Определение оптимальных условий
светогидравлической промывки.
Как известно, для поиска оптимума, наиболее простым с точки зрения выполнения, является экспрессный метод, называемый «методом крутого восхождения».
Суть метода состоит в том, что если поставить серию опытов. В которых в каждом последующем варианте изменять величину действующих факторов пропорционально произведению коэффициента регрессии данного фактора на величин единицы варьирования, то такое движение по поверхности отклика будет кратчайшим путем к достижению оптимума. В рассматриваемом случае:
X1 …0X1 = 200
X2 …0X2 = 4
X3 … 0X3 = 5
λ1 1 =100
λ2 1 =2
λ3 1 =3
b1 =3,18
b2 =2,02
b3 =-0,18
b1 λ1 1 = 318
b2 λ2 1 = 4,04
b3 λ3 1 = -0,54
В качестве «шага» выбираем величину 0,05 b1 λ1 . Тогда план «крутого» восхождения будет выглядеть так, как представлено в таблице 5.
Таблица 5.
Вари- ант |
Условия в кодированном виде | |||||
Х Х Х |
0Х1 0Х2 0Х3 |
0+0,05b1 λ1 0+0,05b2 λ2 0+0,05b3 λ3 |
0+0,1b1 λ1 0+0,1b2 λ2 0+0,1b3 λ3 |
0+0,15b1 λ1 0+0,15b2 λ2 0+0,15b3 λ3 |
0+0,2b1 λ1 0+0,2b2 λ2 0+0,2b3 λ3 |
0+0,25b1 λ1 0+0,25b2 λ2 0+0,25b3 λ3 |
Вари- ант |
Условия в реальном виде | |||||
Х Х Х |
200 4 5 |
215 4,2 4,975 |
230 4,4 4,95 |
245 4,6 4,925 |
260 4,8 4,9 |
275 5,0 4,875 |
| Выход | 10,78 | 13,22 | 14,62 | 15,06 | 16,46 | 17,86 |
Реализованный опыт показал, что принятое решение о проведении крутого восхождения верно. Выход процесса при Х1 = 275, Х2 = 5,0 и Х3 = 4,875 более чем в полтора раза выше, чем на исходном нулевом уровне. Можно сделать предположение о том, что оптимум находится именно при таком сочетании значений рассматриваемых факторов.
Чтобы убедиться в правильности принятого решения о нахождении оптимума был поставлен дополнительный эксперимент с центром в точках ОХ1 = 275; ОХ2 = 5,0; ОХ3 = 4,875.
Шаг варьирования выбираем мельче, чем при ранее проводившихся опытах. Пусть:
λ1 1 = 5; λ2 1 = 0,05; λ3 1 = 0,05.
Таблица 6.
| Тогда | ОХ | + I | - I | |
| W (X) | 275 | 5 | 280 | 270 |
| 2r (X) | 5,0 | 0,05 | 5,05 | 4,95 |
| Пк (X) | 4,875 | 0,05 | 4,925 | 4,825 |
Таблица 7.
| Вариант | Х0 | Х1 | Х2 | Х3 | УN 1 | УN 2 | УN 3 |
УN |
| 1 | + | - | - | - | 17,85 | 17,85 | 17,85 | 17,850 |
| 2 | + | + | - | + | 17,85 | 17,86 | 17,85 | 17,853 |
| 3 | + | - | - | + | 17,85 | 17,85 | 17,86 | 17,853 |
| 4 | + | + | - | - | 17,86 | 17,85 | 17,86 | 17,856 |
| 5 | + | - | + | + | 17,85 | 17,86 | 17,85 | 17,853 |
| 6 | + | + | + | - | 17,86 | 17,86 | 17,86 | 17,860 |
| 7 | + | - | + | - | 17,85 | 17,86 | 17,85 | 17,853 |
| 8 | + | + | + | + | 17,85 | 17,86 | 17,85 | 17,853 |
Коэффи- циент регрессии |
17,853 | 0,016 | 0,016 | 0,016 |
Определяем построчную дисперсию
S1 2 (yN k ) = 0
S2 2 (yN k ) = 0,002454
S3 2 (yN k ) = 0.002454
S4 2 (yN k ) = 0.0034
S5 2 (yN k ) = 0.002454
S6 2 (yN k ) = 0
S7 2 (yN k ) = 0
S8 2 (yN k ) = 0.002454
Рассчитываем дисперсию воспроизводимости:
S2 IУI = 0,00165
Дисперсия среднего значения:
_
S2 IУI = 0,00055
Дисперсия коэффициентов регрессии:
S2 (bi) = 0,00007
по которой находится ошибка коэффициентов регрессии:
S2 IbiI = √0,00835 = 0,00835
Критерий значимости:
S2 IbiIt (f‘) = 0,00835 2,12 = 0,0177
Все коэффициенты светогидравлической промывки получились незначительными, следовательно в рассматриваемом случае оптимальными условиями можно считать следующие:
- величина энергии светового импульса лазера должна лежать в пределах 50 милли Ватт в каждом импульсе;
- диаметр капли промывочной жидкости должна составлять 0,5 мкм;
- показатель преломления промывочной жидкости составляет 2%.
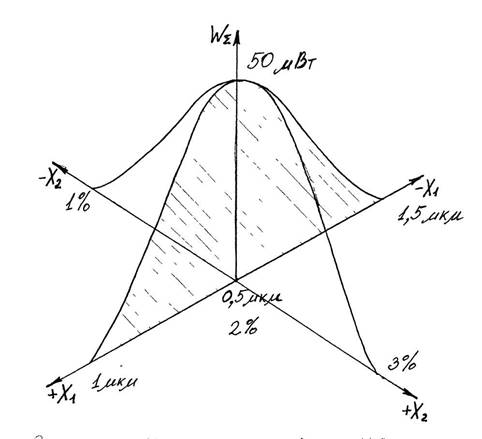
Рис 1. Поверхность отклика.
На рисунке 1 приведена поверхность отклика, полученная в результате графического представления описанного опыта. Анализ этой поверхности показывает, что полученные условия являются оптимальными лишь для выбранного типа лазерного оборудования, параметров жидкой рабочей среды и катализатора. Очевидно, что дальнейшее увеличение энергии лазера (невозможно для данного типа лазера) может дать приращение значений выходного параметра, так же как увеличение диаметра капли (невозможное вследствие отрыва капли диаметром более 6 мм от патрубка).
2. Разработка структурной схемы установки для светогидравлической промывки и оценка его возможностей применения в промышленности.
Разнообразие решаемых конкретных технологических задач определяет и различные требования к параметрам светогидравлических установок, что в свою очередь, приводит к большому количеству их схем построения. В данном разделе рассмотрим основные элементы и методы построения технологических лазерных установок, использующих энергию светогидравлического эффекта.
2.1. Разработка структурной схемы установки для светогидравлической промывки.
Анализ схем возможных вариантов светогидравлической обработки позволил разработать общую структуру технологических установок, использующих этот принцип (рис. 2.1).
Источником энергии в установке является лазер [2], излучение которого через оптическую систему направляется в камеру светогидравлического устройства. Взаимодействие всех элементов, образующих схему установки, регулирует блок управления (Б.У.) [3].
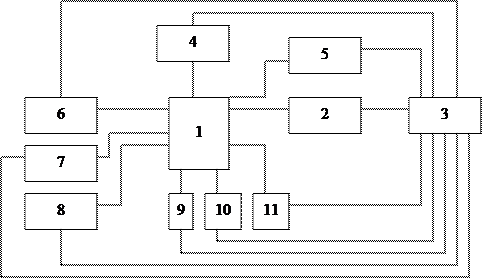 |
Рис 2.1. Общая структурная схема установок для светогидравлической промывки.
1 – рабочая камера;
2 – лазер с оптической системой;
3 – блок управления (Б.У.);
4 – блок герметизации рабочей камеры;
5 – блок вакуумирования рабочей камеры;
6 – блок регистрации уровня жидкости в рабочей камере;
7 – блок подачи жидкой среды в рабочую камеру;
8 – блок слива отработанной жидкой среды;
9 блок тарированной подачи капель промывочной жидкости в рабочую камеру;
10 – блок измерения спектрографических характеристик промывочной жидкости.
11 – датчик устройства встроенного контроля качества выполнения операции.
Герметизация камеры осуществляется за счет механизма прижима [4], в котором одновременно предусмотрен датчик для измерения силы прижима. По достижении заданного значения усилия прижима подается сигнал на Б.У., который отключает механизм 4 и подает сигнал на включение блока 5, представляющего собой устройство вакуумирования рабочей камеры.
Величина достаточного вакуума регистрируется и по достижении заданного его значения подается сигнал на Б.У. об отключении блока 5 и последующих блоков.
В подготовленную таким образом камеру подается жидкая рабочая среда за счет устройства 7, часть жидкости при этом перетекает в специальную емкость водного затвора, в которой уровень ее регистрируется блоком , который после достижения заданного уровня подает на Б.У. сигнал о прекращении подачи жидкой среды и включении в работу блока 9.
В жидкую рабочую среду вводятся капли за счет блока тарированной подачи 9 и одновременно ведется измерение его количества. По достижении заданного параметра на Б.У. подается сигнал, прекращающий подачу капель. Одновременно с введением капель Б.У. подает команду на зарядку блока конденсаторов лазера 2.
Блок управления подает команду на включение в работу лазера. За счет светогидравлического эффекта в камере создается облако капель промывочной жидкости, характеристики которых регистрируются блоком 10.
Качество выполнения операции может регистрироваться с помощью датчиков встроенного контроля (блок 11), которые подаются блоком 10.
Качество выполнения операции может регистрироваться с помощью датчиков встроенного контроля (блок 11), которые подают сигналы на Б.У. В случае невыполнения заданных требований Б.У. выдает команду на повторение операции, а при достижении требуемого качества – на блок 8, который сливает обработанную жидкую среду и катализатор, и приводит все элементы установки в исходное состояние.
Выбор конкретной конструкции и параметров всех перечисленных элементов установки зависят, как уже указывалось, от вида решаемой технологической задачи.
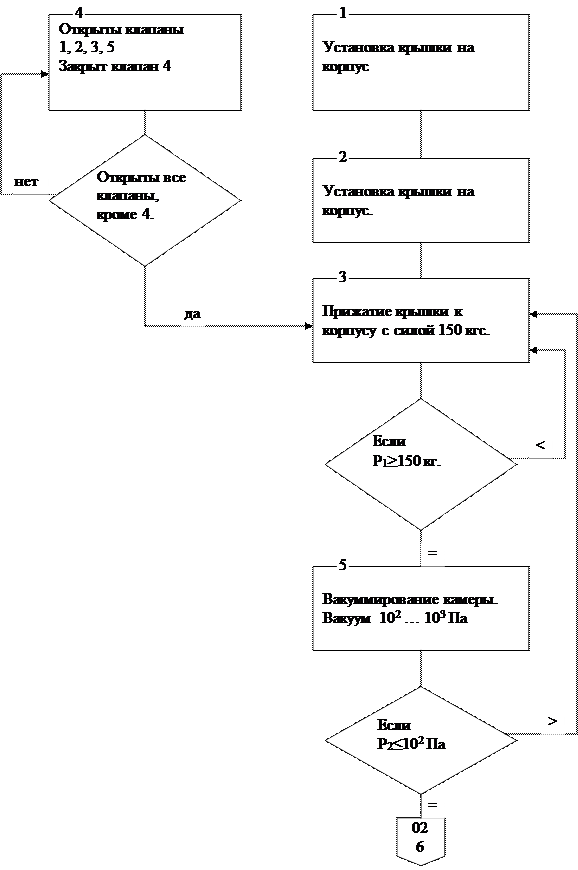
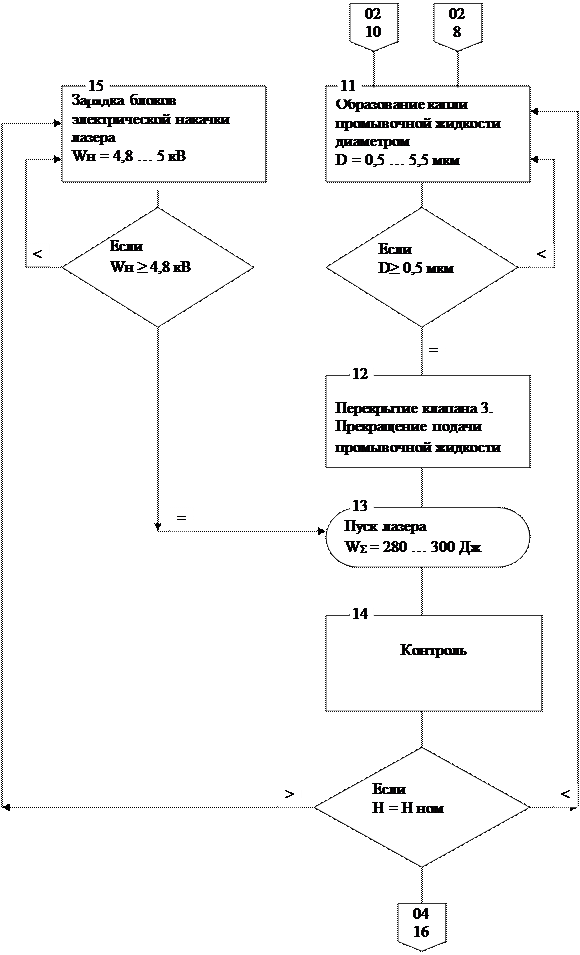
Рис.2.2. Алгоритм работы лабораторного образца установки для светогидравлической
промывки.
Лист 01.
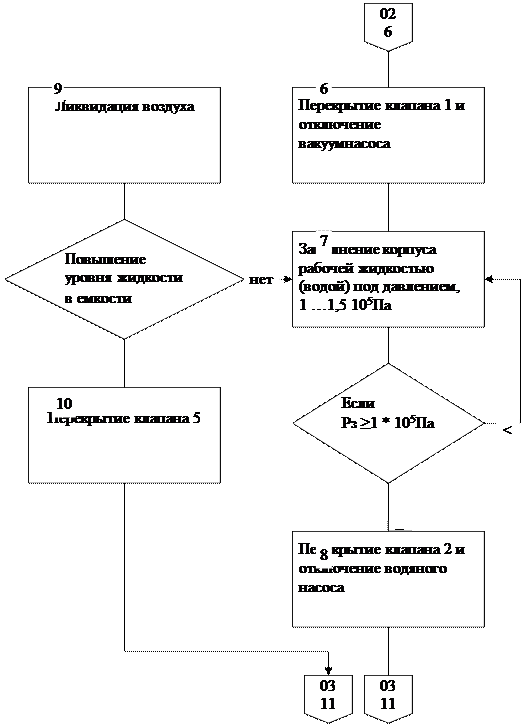 |
Лист 02.
Лист 03.
 |
||
 |
||
 |
||
 |
||
 |
||
Лист 04.
Рис.2.2. Алгоритм работы лабораторного образца установки для светогидравлической промывки.
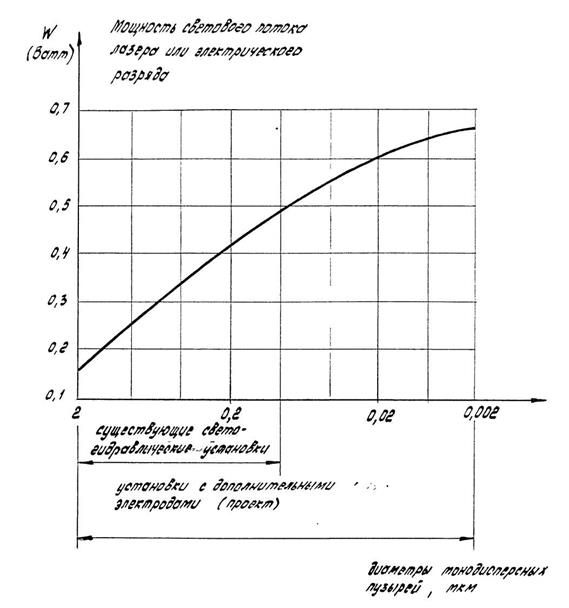
Рис. 2.3. зависимость диаметра монодисперсных парожидкостных микропузырей очищающей жидкости от мощности светового потока лазера.
3. Расчет оптического тракта установки для промывки.
В оптический тракт установки входят элементы, каждый из которых обладает определенной поглощающей и отражающей способностью.
Основным элементом, поглощающим световую энергию лазера, является парожидкостной пузырек.
Когда парожидкостный пузырек взрывоподобно вскипает, поглощая основную долю световой энергии, причем при схлопывании пузырька имеют место кавитационные явления.
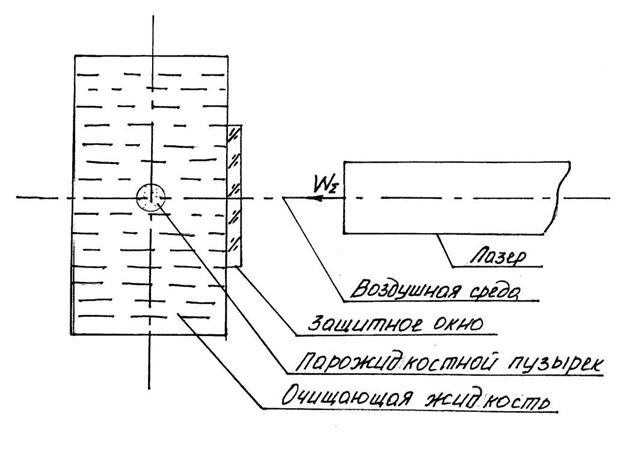
Рис. 2.4. Оптический тракт установки для промывания.
Под действием кавитационных явлений с одной стороны происходит очищение заготовки, а с другой стороны вместо большого парожидкостного пузырька диаметром порядка 0,2 мм образуются мелкие пузырьки диаметром от 2 до 0,2 мкм, соизмеримые по своим геометрическим параметрам с геометрическими параметрами микротрещин на поверхности заготовки.
Таблица 8.
Отражательная и поглотительная способность элементов оптического тракта.
№ п/п |
Элемент оптического тракта |
Отражающая способность |
Поглощающая способность. |
| 1 | Лазер с выходной мощностью () | - | - |
| 2 | Воздушная среда | 0,001 от WΣ | 0,001 от WΣ |
| 3 | Защитное окно | 0,001 от WΣ | 0,001 от WΣ |
| 4 | Очищающая жидкость | 0,001 от WΣ | 0,001 от WΣ |
| 5 | Парожидкостный пузырек | 0,01 от WΣ | 0,99 от WΣ |
Список используемой литературы.
1. Адлер Ю.П., Макарова Е.В., Грановский Ю.В. «Планирование эксперемента при поиске оптимальных условий». М.:Наука, 1981. – 281 с, ил.
2. Андреева Л.Е. «Упругие элементы приборов». М.: Машгиз, 1982. – 455 с., ил.
3. Аренков А.Б. «основы электрофизических методов обработки материалов».:Машиностроение,, Ленинградское отд-ние, 1967. – 372 с., ил.
4. Анучин М.А. и др. «Штамповка взрывом. Основы теории». М.: Машиностроение, 1972. – 150 с., ил.
5. Апанасевич П.П. «Основы теории взаимодействия света с веществом». Минск.: Наука и техника, 1977. – 495 с., ил.
6. Аскарьян Г.А., Прохоров А.М., Чантурия Г.Ф., Шипуло Г.П. «Луч ОКГ в жидкости». в журнале: журнал экспериментальной и технической физики, т. 44, в. 6, 1963, с 2180 – 2182.
7. Ахиманов С.А., Хохлов Р.В. «Проблемы нелинейной оптики». М.: Наука, 1964. – 155 с., ил.
8. Басов Н.Г., Кологривов А.А., Крохин О.Н. др. «Наблюдение сжатия полых микросфер, облучаемых лазером». – в журнале: Письма в ЖЭТФ, т. 23, в. 8, 1976, с. 752 – 753.
9. Баринов В.В., Сорокин С.А. «Взрывы водных капель под действием оптического излучения». - в журнале: Квантовая электроника. 2 (14), 1973, с. 5 – 11.
10. Батуев Г.С., Голубков Ю.В., Ефремов А.К., «Инженерные методы исследования ударных процессов». М.: Машиностроение, 1977. – 239 с., ил.
11. Бломберген Н. «Нелинейная оптика». Пер. с англ. М.: Мир, 1966. – 865 с., ил.
12. Бойер К. «О возможности использования в РД термоядерной реакции, инициируемой лазером». В журнале: Вопросы ракетной техники, №7, 974, с. 74 – 82.
13. Борадочев И.А. «основные вопросы теории точности производства». М.: Изд. Академии наук СССР, 1950. – 388 с., ил.
14. Базуков А.А., Попов Ю.А., Тесленко В.С. «Экспериментальное излучение взрывного процесса, вызванного фокусировкой моноимпульсного излучения лазера в воду». В журнале: ПМТФ, №5, 17, 1969, с. 17 – 24.
15. Букздорф Н.В., Погодаев В.А., Чистяков Л.К. «О связи неоднородностей внутреннего оптического поля облученной капли с ее взрывом». В журнале: Квантовая электроника, т. 2, №5, 1975, с. 1062 – 1064.
16. Бункин В.Ф., Конов В.И. и др. «Светоакустическая кавитация в воде». В журнале: ЖЭТФ, №67, в. 6 (12), 1974, с. 2087 – 2091.
17. Вукс М.Ф. «Рассеяние света в газах, жидкостях и растворах. Л.: изд. Ленинград. ун-та, 1977. – 320 с., ил.
18. Гаврилов А.Н. «Технология авиационного приборостроения». М.: Оборонгиз, 1962. – 365., ил.
19. Замышляев Б.В., Яковев Ю.С. «Динамические нагрузки при подводном взрыве. Л.: Судостроение, 1967. – 158 с., ил.
20. Зельдович Я.Б. «Теория ударных волн.» М.: Изд. АН СССР, 1946. – 482 с., ил.
21. Иоффе А.И., Мельников Н.А., Наугольных К.А., Упадышев В.А. «Ударная волна при оптическом пробое в воде». В журнале: ПМФТ, №3, 225, 1970. с. 18 – 22.
22. Картавов С.А., Коваленко В.С. «Применение ОКГ для технологических целей». Киев: Техника, 190 – 275 с., ил.
23. Кей Дж., Леби Т. «Таблицы физических и химических постоянных». Изд. Второе переработанное. Перевод с англ. М.: Гос. изд физико-матем. Литературы, 1962. – 247 с.
24. Конингстайн И.А. «Введение в теорию комбинационного рассеяния света». М.: Мир, 1975. – 375 с., ил.
25. Кошелев К.Н., Чекалин С.В., Чурилов С.С. «Об оптической фокусировке лазерного излучения на поверхности твердой мишени». В журнале: Квантовая электроника, т. 2 №7, 1975, с. 1593 – 1596.
26. Кракстон к. «Физика жидкого состояния. Статическое введение». Перевод с англ. М.: Мир, 1978. – 565 с., ил.
27. Кузиковский А.В. «Динамика сферической частицы в мощном оптическом поле». В журнале: Известия ВУЗов Физика. №5, 1970, с. 89 – 94.
28. Ландау Л.Д. «Об ударных волнах на далеких расстояниях от места их возникновения». – В журнале: ПММ, т. IX, вып. 4, 1945, с. 18 – 22.
29. Ландау Л.Д., Лившиц Е.М. «Механика сплошных сред». – М: Готехиздат, 1954 – с., ил.
30. Леонов Р.К., Таурин Н.Ф. и др. «О роли кавитации в световом разрушении поверхности стекла, контактирующего с жидкостью». В журнале: Физика и химия обработки материалов, №6, 1974. с. 22 – 23.
31. Лихачев А.П. «Лазерный способ исследования веществ при сверхвысоких температурах и давлениях». В журнале: Геохимия, №10, 1978, с. 25 – 28.
32. Лосев С.А. «Газодинамические лазеры». М.: Наука, Глав. ред.физ. мат. лит., 1977. – 255 с., ил.
33. Миркин Л.И. «Физические основы обработки материалов лучами лазера». М.: Изд. Московского университета, 1975, 162 с., ил.
34. Най Дж. «Физические свойства кристаллов». М.: Мир, 1967, 375 с., ил.
35. Наугольных К.А., Рой Н.А. «Электрические разряды в воде». М.: Наука, 1971, 153 с., ил.
36. «Оборудование и технологические продессы с использованием электрогидравлического эффекта». Под ред. к.т.н. Г.А. Гулого. М.: Машиностроение. 1977, 320 с., ил.
37. Огибалов П.М., Кийко И.А. «Очерки по механике высоких параметров. Сб. науч. тр. Московского университета». М.: МГУ, 1966, 151 с.
38. Перник А.Д. «Проблемы кавитации». М.: Судпромгиз, 1963, 382 с., ил.
39. Пиховиков Р.В., Завьялова В.И. «Штамповка листового металла взрывом» м.: Машиностроение, 1984, 152 с., ил.
40. Пустовалов В.К., Романов Г.С. «Испарение капли в диффузном режиме под действием монохроматического излучения». В журнале: Квантовая электроника, 4, №1, 1977, с. 84 – 94.
41. Рейнхарт Дж.С., Пирсон Дж. «Взрывная обработка металлов». М.: Мир, 1966, 220 с., ил.
42. Ринкевичус Б.С. «Лазерная анемометрия». М.: Энергия, 1978, 159 с., ил.
43. Рыкалин Н.Н., Углов А.А. «Процессы объемного парообразования». В журнале: ТВТ, т. 9, №3, 1971, с. 575 – 582.
44. Степанов В.Г., Шавров И.А. «Высокоэнергитические импульсные методы обработки материалов». Л.: Машиностроение, 1975, 277 с., ил.
45. Суминов В.М., Чуреев Е.Г. «Оценка технологических возможностей энергии светогидравлического эффекта для обработки деталей. Труды научно-технической конференции по технологии и конструированию микроэлектронных устройств». М.: Электроника, 1980, 451 с., ил.
46. А.С. 220207 «Устройство для штамповки листовых заготовок». (Суминов В.М., Чуреев Е.Г.) – Публикация запрещена.
47. А.С. 278617 «Устройство для штамповки листовых заготовок». (Суминов В.М., Чуреев Е.Г.) – Публикация запрещена.
48. А.С. 577733 «Устройство для штамповки оптическим квантовым генератором». (Суминов В.М., Чуреев Е.Г.) опубл. в Б.И., 1978, №9.
49. А.С. 597143 «Устройство для гидролазерной штамповки». (Суминов В.М., Чуреев Е.Г.) опубл. в Б.И., 1978, №9.
50. А.С. 674300 «Устройство для штамповки оптическим квантовым генератором». (Суминов В.М., Чуреев Е.Г.) – Публикация запрещена.
51. Суминов В.М. «Гидролазерная штамповка». В журнале: Авиационная промышленность, №10, 1970, с. 47 – 50.
52. Суминов В.М., Промыслов Е.В., Скворчевский А.К. «Обработка деталей лучом лазера». М.: Машиностроение, 1976, 196 с., ил.
53. Суминов В.М., Скворчевский А.К. «Уравновешивание вращающихся тел лучом лазера». М.: Машиностроение, 1974, 175 с., ил.
54. Суминов В.М., Чуреев Е.Г. и др. «Технологическое лазерное оборудование в машиностроении и приборостроении. Каталог ВДНХ». М.: Машиностроение, 1974, 24 с., ил.
55. Суминов В.М., Чуреев Е.Г. «Исследование светогидравлического эффекта и оценка его технологических возможностей. Тезисы докладов II Всесоюзной конференции. «Применение лазеров в приборостроении, машиностроении и медицинской технике»».М.: МВТУ, 1979, 34 с.
56. А.С. 752901 «Способ создания импульсного давления». (Суминов В.М., Чуреев Е.Г.) – Публикация запрещена.
57. А.С. 849613 «Устройство для электрогидравлической обработки» (Суминов В.М., Чуреев Е.Г.) – Публикация запрещена.
58. Тесленко В.С. «Исследование светоакустических и светогидродинамических параметров лазерного пробоя в жидкостях». В журнале: Квантовая электроника. Т. 4, №8, 1977., с 1732 – 1737.
59. Чуреев Е.Г. «Взаимодействие лазерного излучения с различными материалами в жидкости». РФ. Физика, 1977, №7, Реферат 7Д 1240. Дер. В ЦНИИТЭИ приборостроения 26 авг. 1976 г., №604.
60. Чуреев Е.Г. «Взаимодействие светового излучения с легко испаряющимися жидкостями и металлами в воде». В журнале: Известия ВУЗов по разделу «Приборостроение», т.ХХП, №12, 1979, с. 71 – 75.
61. Юткин Л.А. «Электрогидравлический эффект». М.: Машгиз, 1955, 35 с., ил.
62. Чуреев Е.Г. «Светогидравлический эффект и его применение в космической технологии. Тезисы доклада на 1-ом Международном аэрокосмическом когрессе». Москва, 1994 г.
63. Чуреев Е.Г. «Светогидравлический эффект и его место в механике жидких сред. Тезисы доклада на 7-ом Международном симпозиуме «Применение лазеров в механике жидких сред.»» Лиссабон, Португалия, Институт высоких технологий, 1996 г.
64. Чуреев Е.Г. «Технологическое применение светогидравлического эффекта». Лиссабон, Португалия, Институт высоких технологий, 2001 г.
65. Чуреев Е.Г., Чувпило Г.А. «Механика жидких сред как научная основа технологического применения светогидравлического эффекта». Лиссабон, Португалия, Институт высоких технологий, 2003 г.
66. Чуреев Е.Г. Чувпило Г.А. «Разработка оборудования для стерилизации медицинских инструментов» Отчет по гранту №2483, С.Петербург, центр грантов, 1996 г.