| Скачать .docx |
Реферат: Модуляторы, дефлекторы, фильтры, процессоры, генератоы. Усилители и фазовозвращатели
Министерство образования Республики Беларусь
Учреждение образования
“Белорусский государственный университет
информатики и радиоэлектроники”
кафедра ЭВС
РЕФЕРАТ
На тему:
"Модуляторы, дефлекторы, фильтры, процессоры, генератоы. Усилители и фазовозвращатели"
МИНСК, 2008
Принцип действия фильтров на поверхностных акустических волнах (ПАВ). На принципах функциональной электроники, а именно на использовании динамических неоднородностей, можно построить фильтры не только на основе ПЗС, но и акустоэлектронные, основанные на применении поверхностных акустических волн. При многих замечательных качествах фильтров на ПЗС их максимальная рабочая частота ограничена примерно 20 МГц. Акустоэлектронные фильтры, основанные на создании и движении динамических неоднородностей в виде дискретных упругих деформаций, удачно дополняют фильтры на ПЗС, так как рабочий диапазон частот фильтров на ПАВ находится в пределах от 1 до 103 МГц.
Напомним, что фильтры, использующие акустические объемные колебания, имеют следующие недостатки: существенно ограничены высшие частоты (для магнитострикционных фильтров - несколько мегагерц, для пьезоэлектрических 10 … 30 МГц); конструкция и технология этих фильтров основаны на механической обработке с очень высокой точностью, т.е. они отличаются по конструкции и технологическим процессам изготовления от современных элементов РЭА, базирующихся на микроэлектронике; по конфигурации и размерам, несмотря на их компактность (по сравнению с электрическими фильтрами), они плохо согласуются с конструкциями ИС.
Фильтры на поверхностных акустических волнах имеют принципиальные преимущества перед другими фильтрами, основанными на эффекте преобразования электрических колебаний в акустические. В устройствах на ПАВ объемные волны не применяются. В связи с этим изменяется принцип их действия и технические возможности.
Для того чтобы использовать поверхностные волны для создания фильтров, необходимо с помощью электрических сигналов во входном преобразователе возбудить их, а затем в выходном преобразователе вновь превратить в электрические сигналы.

Рис.1.
Поверхностные акустические волны формируют тонкий, соизмеримый с длиной волны, слой с динамическими неоднородностями в виде упругих деформаций, имеющих дискретный характер. Это позволяет преобразования электрических волн в акустические во входном преобразователе и обратно в выходном осуществлять путем использования тонких металлических штырей (электродов), напыленных на поверхности звукопровода (подложки), обладающего пьезоэлектрическим эффектом.
Существует много методов возбуждения поверхностных волн. Рассмотрим метод, основанный на использовании в преобразователе встречных штырей (ВШП - встречно штыревые преобразователи). Он удачно сочетается с технологическими методами микроэлектроники. Схематично такой преобразователь показан на рис.1, где 1 - входной преобразователь; 2 - выходной преобразователь; 3 - поглотитель; 4 - звукопровод; 5 - штыри (напыленные металлические электроды).
Основными разновидностями ВШП являются: эквидистантный преобразователь (с одинаковыми расстояниями между штырями); неэквидистантный преобразователь (с различными расстояниями между штырями); неаподизованный преобразователь (с одинаковыми перекрытиями штырей); аподизованный (взвешенный) преобразователь (с различной степенью перекрытия штырей) и др.
Как видно из рис.1, если приложить к штырям входного преобразователя электрическое напряжение высокой частоты, обеспечить согласование частоты f с шагом ВШП, то под влиянием поля произойдет деформация в пьезоэлектрике, которая со скоростью υпов распространится в обе стороны от каждого промежутка, если a - ширина штырей, h - расстояние между штырями; то шаг ВШП
| b=a+h. | (1) |
Если шаг ВШП согласован с длиной волны, то деформации, вызванные каждым промежутком, суммируются, образуя суммарную поверхностную волну.
Суммирование происходит за счет того, что локальная деформация, образовавшаяся под одним из промежутков, начинает перемещаться в противоположных направлениях и проходит расстояние λпов /2 до следующего промежутка. Она оказывается там в тот момент, когда следующая полуволна внешнего напряжения достигнет максимума и создаст свою деформацию, которая, складываясь с пришедшей от соседнего промежутка, создаст суммарную деформацию. Это имеет место при выполнении равенства
| 2b=λпов= υпов/f, | (2) |
где λпов - длина поверхностной акустической волны.
Так происходит многократно под всеми промежутками, и суммарная волна распространяется по звукопроводу. Эта волна достигает выходного преобразователя, где происходит обратное преобразование деформаций в электрическое напряжение. Обратное преобразование обусловлено тем, что деформации пьезоэлектрика, вызванные поверхностной волной, приводят к появлению электрического напряжения, наведенного на соседних парах штырей при согласовании ВШП с частотой, будет противоположный из-за обратного чередования штырей. Это позволяет сформировать в выходном преобразователе двуполярное переменное электрическое напряжение с частотой входного сигнала.
Чем больше штырей содержит преобразователь, тем он эффективнее и тем большая накапливается деформация. Одновременно с этим более жесткие требования предъявляются к точности выполнения штырей звукопровода, к стабильности скорости распространения поверхностной волны и частоты сигнала. Очевидно, что суммирование будет иметь место только при (a+h) = λпов /2. деформации, возникающие под промежутками при других частотах, не будут эффективно суммироваться. Зависимость отклика от частоты можно использовать для получения эффекта фильтрации.
Очевидно, свойства таких фильтров зависят от материала звукопровода. Например, для ниобата лития (LiNbO3) скорость поверхностной волны составляет от 3,48 до 4 км/с в зависимости от среза, квадрат коэффициента электромеханической связи составляет 0,05; температурный коэффициент задержки - 85×10-6 1/°С. Тогда, например, при частоте 100 МГц длина поверхностной акустической волны
| λпов=υпов/f=4000 м/с/100·106 Гц =4·10-2 мм. | (3) |
При этом шаг ВПШ
| (4) |
Отметим важную особенность фильтров на ПАВ: они являются дискретными аналогично фильтрам на ПЗС. Действительно, электрическое поле действует на пьезоэлектрик, вызывая неоднородность, в виде дискретных участков сжатия или растяжения, где расположены пары штырей преобразователя. Распространяясь, неоднородности суммируются. Следовательно, к таким фильтрам можно применить многие соображения, касающиеся особенностей характеристик.
Из принципа действия фильтров на ПАВ очевидно, что если штыри и промежутки выполнить точно и согласованно с частотой, то полоса частот пропускания определяется числом пар штырей. Действительно, при малом числе пар штырей отклонение частоты от средней (расстройка) приводит к уменьшению эффективности преобразования и, следовательно, к частотно-избирательному эффекту, но уменьшение коэффициента передачи с расстройкой происходит медленно. Если же использовать много пар штырей, то каждая пара будет вносить свою долю в уменьшение относительного коэффициента передачи, т.е. в этом случае полоса частот будет более узкая. Это полностью согласуется с соображениями, изложенными ранее, когда подчеркивалось, что фильтрация есть процесс накопления, так как при большом количестве штырей накапливается много воздействий, формирующих поверхностную акустическую волну.
Между числом электродов преобразователя и его полосой существует следующая взаимосвязь:
| ∆fп=f0/N, | (5) |
где ∆fп - полоса пропускания частот фильтра; N - число пар штырей; f0 - центральная частота фильтра.
Напомним, что добротность LC-контура Q= f0/∆fп. Следовательно, число пар штырей эквивалентно добротности. Отсюда следует, что сужение полосы пропускания фильтра связано с увеличением числа штырей, т.е. с увеличением размеров фильтра. Однако ограничение, связанное с сужением полосы пропускания в LC-фильтрах, более жесткое, так как определяется природой потерь в конденсаторе и катушке индуктивности, которые не могут быть уменьшены ниже определенного уровня. В данном случае полоса пропускания ограничивается в основном возможностями технологии, которая определяет количество пар штырей и размеры звукопровода. Следовательно, в этом смысле фильтры на ПАВ имеют те же свойства, что и фильтры на ПЗС, для которых было показано, что полоса определяется числом секций МДП-конденсаторов (элементов памяти).
Из изложенного принципа действия вытекает, что фильтры на ПАВ по природе функционирования являются полосовыми со средней частотой, зависящей от размеров штырей. Идеи, положенные в основу работы фильтров на ПАВ, использованы для создания устройств различного функционального назначения: полосовых входных фильтров и фильтров на УПЧ; линий задержки на фиксированную задержку и с отводами; фильтров для приема сложных шумоподобных (ШПС), фазоманипулированных (ФМН) сигналов с большой базой; фильтров для приема линейно-частотно-модулированных сигналов с большой базой; резонаторов на ПАВ и других устройств.
В последующем изложении будет рассмотрен наиболее распространенный вариант - полосовой фильтр с эквидистантными преобразователями. Особенности некоторых других будут рассмотрены в конце параграфа.
Область частот фильтров на ПАВ. Минимальная частота фильтра на ПАВ определяется возможными размерами звукопровода, которые зависят от технологии изготовления и составляют обычно не больше 50 … 300 мм, а также от требований к относительной полосе частот, т.е. от количества пар штырей и числа преобразователей.
Минимальное число преобразователей в фильтре два: входной, куда поступает фильтруемый сигнал, и выходной, который воспринимает отфильтрованный сигнал. Функции фильтрации могут быть распределены между ними по-разному. Наиболее часто основные функции по формированию частотной характеристики выполняет входной преобразователь, а выходной является широкополосным. Как показывает опыт, при этом меньше проявляются искажения частотной характеристики.
Суммарная амплитудно-частотная характеристика (АЧХ) фильтра Kф(ω) определяется произведением частотных характеристик обоих преобразователей:
| Kф(ω) = Kвх(ω) Kвых(ω), | (6) |
поэтому детальное рассмотрение АЧХ можно проводить для каждого преобразователя в отдельности.
Отметим, что для фильтров на ПАВ большое значение имеет относительное расположение преобразователей. Их не располагают далеко друг от друга, так как удаление вызывает дополнительные искажения АЧХ. Это согласуется с требованием уменьшения габаритов и получения фильтров на возможно более низкие частоты.
Используя соотношение между длиной преобразователя (рис.2, а) и полосой частот, определим, на какой минимальной частоте может работать фильтр. Предположим, что lз<< lвх и lвых<< lвх, где lз - расстояние между преобразователями; lвх - ![]() длина входного преобразователя; lвых - длина выходного преобразователя. Тогда минимальную частоту настройки фильтра можно приближенно определить рассматривая один входной преобразователь. Минимальное число пар штырей и, следовательно, низшая частота фильтра зависят от требований к относительной полосе пропускания частот. Если взять типичный случай, когда ∆fп=0,05f0, то требуется 20 пар штырей. Длина входного преобразователя будет равна lвх=10 λпов. При скорости распространения.
длина входного преобразователя; lвых - длина выходного преобразователя. Тогда минимальную частоту настройки фильтра можно приближенно определить рассматривая один входной преобразователь. Минимальное число пар штырей и, следовательно, низшая частота фильтра зависят от требований к относительной полосе пропускания частот. Если взять типичный случай, когда ∆fп=0,05f0, то требуется 20 пар штырей. Длина входного преобразователя будет равна lвх=10 λпов. При скорости распространения.

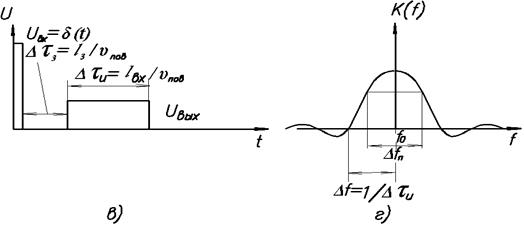
Рис.2.
поверхностной волны υпов≈3000 м/с, считая, что звукопровод позволяет создать преобразователь длиной lвх≈100 мм, получим, что минимальная частота сигнала составит около 200 кГц. Реально, с учетом расстояния между преобразователями lз, длины выходного преобразователя, технологических промежутков, частота составит примерно 400 кГц. Следовательно, низшая частота фильтра определяется возможной длиной звукопровода. На практике фильтры на ПАВ используются на частотах выше 1 МГц.
Технология ВШП должна обеспечивать высокую разрешающую способность, чтобы с высокой точностью выдерживать очень маленькие размеры как ширины штырей, так и промежутка между ними и шага в целом. Сказанное ограничивает высшие частоты. Например, если исходить из того, что с достаточной точностью могут быть выполнены штыри и промежутки между ними шириной в 1 мкм, то высшая частота настройки преобразователя и, следовательно, фильтра составит
| f= υпов /2 kм =4000/2(1+1) =1·109 Гц. | (7) |
Следовательно, фильтры на ПАВ могут работать на достаточно высоких частотах.
Расчет частотных характеристик. Для практического использования фильтра важны ширина полосы и форма частотной характеристики.
При расчете частотной характеристики фильтра на ПАВ возникают трудности, вызванные тем, что электрическое поле и связанные с ним поверхностные акустические волны имеют сложную структуру. Поэтому для инженерных расчетов необходимо создать методику, которая должна позволить сохранить основные особенности поля и акустических волн и в то же время существенно упростить расчет АЧХ.
Основное применение для расчета получил метод δ-функций. Для получения расчетных соотношений для частотной характеристики предположим, что на штыри эквидистантного преобразователя действует сигнал в виде очень короткого импульса напряжения (δ-функция). В этом случае в каждом из промежутков между штырями возбуждается кратковременно электрическое поле. Вдоль звукопроврда будет двигаться поверхностная волна с λпов=2(a+h). Протяженность импульса этой волны в звукопроводе определяется не длительностью электрического импульса, а шириной входного преобразователя lвх. Огибающая этого импульса ∆l=lвх и направление его движения в одну из сторон показаны на рис.2, б. импульс длительностью ∆l=lвх со скоростью υпов двигается к выходному преобразователю. Для того чтобы этот преобразователь мало влиял на частотную характеристику, предположим, что он состоит из одной пары штырей. Импульс, проходя через выходной преобразователь с задержкой ∆τз= lз/ υпов, дает на радиочастоте f0=υпов/ /2(a+h) импульс напряжения с длительностью ∆τз≈ lвх/ υпов (рис.2, в). Так как
| lвх= λповN, | (8) |
то
| ∆τи=N/f0 | (9) |
Известно, что импульс такой длительности на несущей частоте имеет спектр частот с огибающей [sinNπ ((f-f0) /f0)] / [Nπ ((f-f0) /f0)] (рис.2, г). Высокочастотное заполнение для упрощения рисунка не показано. Как видно, полоса пропускания между "нулями" на частотной характеристике
| 2∆f0=2(1/∆τи) =2f0/N. | (10) |
Для уровня ослабления, равного 0,7 от максимума (что принято использовать для характеристики полосы пропускания) полная полоса частот в два раза уже:
| ∆fп=f0/N. | (11) |
Так как отклик линейной цепи на δ-импульс есть ее импульсная функция, то импульс длительностью ∆τи на выходе выходного преобразователя тоже импульсная функция фильтра. Преобразование Фурье дает частотную характеристику, следовательно, на рис.2, г показана частотная характеристика фильтра. Эта характеристика имеет дополнительные выбросы и практически малопригодна, поэтому возникает задача значительно уменьшить уровень боковых лепестков (выбросов). Для этого необходимо, чтобы дискретный фильтр имел неоднородную структуру, т.е. чтобы отдельные звенья фильтра вносили разные "вклады".
Структура фильтра, которая была рассмотрена выше, в терминах дискретных фильтров может быть определена как дающая фильтр с "прямоугольным окном". Для того чтобы уменьшить боковые выбросы, нужно использовать сложные формы "окна". Для реализации этой задачи следует решить вопрос о том, как изменить "вклад" каждого звена или каждой пары штырей в формирование результирующей волны. Дискретное возбуждение необходимо осуществлять в разных парах штырей с разной интенсивностью. Интенсивность парциальной волны, возбуждаемой каждой парой штырей, определяется длиной или перекрытием штырей (аналогично тому, как в фильтрах на ПЗС интенсивность снимаемого сигнала определялось перекрытием электродов). Следовательно, нужно брать разные значения перекрытия штырей у преобразователя по его длине. Это изменит форму импульса, описывающего импульсную функцию и, следовательно, обеспечит получение другой формы частотной характеристики, так как они связаны преобразованием Фурье. При проектировании фильтра следует менять перекрытие штырей по длине преобразователя в соответствии заданной импульсной характеристикой, которая определяется из требуемой частотной характеристики. Изменение перекрытия называют аподизацией. Это эквивалентно методу формирования "окон" в общей теории дискретных фильтров. В качестве примера приведем формы частотных характеристик, соответствующие им формы импульса, аналитические выражения частотных характеристик и импульсных функций, а также рисунки перекрытия штырей для эквидистантного преобразователя. При изменении перекрытия штырей по длине преобразователя форма частотной характеристики становится более плавной, выбросы уменьшаются, но ширина полосы увеличивается. Это и понятно, так как уменьшается количество штырей, существенно влияющих на формирование результирующей волны и полосы пропускания.
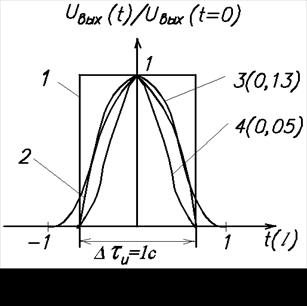
Для доказательства того, как аподизация влияет на форму частотной характеристики и полосу пропускания, воспользовавшись формулами, рассчитаем АЧХ. Сделаем это для нормированной ширины импульса, когда протяженность во времени импульсной переходной функции и соответствующее ей количество штырей, являются одинаковыми для всех случаев (рис.3). для простоты расчета положим, что длительность импульсной функции во всех случаях равна единице. На рис.3: 1 - прямоугольная импульсная характеристика с длительностью 1 с; 2 - импульсная функция в виде треугольника с длительностью 1 с; 3 - импульсная характеристика типа e![]() при α=8, когда в пределах длительности 1 с ордината составляет 0,13 … 1; 4 - импульсная характеристика типа e
при α=8, когда в пределах длительности 1 с ордината составляет 0,13 … 1; 4 - импульсная характеристика типа e![]() при α=12, когда в пределах длительности 1 с ордината составляет от 0,05 … 1.
при α=12, когда в пределах длительности 1 с ордината составляет от 0,05 … 1.
|
4 - при изменении перекрытия
штырей по закону e![]() при α=8 и 12 соответственно. Из рис.4 наглядно видно, что при линейной аподизации интенсивность боковых выбросов составляет 0,05 максимума, а полоса пропускания расширяется (на уровне 0,7) примерно в 1,3 раза, т.е. форма частотной характеристики улучшается по сравнению со случаем равномерного перекрытия штырей. При перекрытии штырей по закону e
при α=8 и 12 соответственно. Из рис.4 наглядно видно, что при линейной аподизации интенсивность боковых выбросов составляет 0,05 максимума, а полоса пропускания расширяется (на уровне 0,7) примерно в 1,3 раза, т.е. форма частотной характеристики улучшается по сравнению со случаем равномерного перекрытия штырей. При перекрытии штырей по закону e![]() частотная характеристика не имеет боковых выбросов, а полоса пропускания расширяется по сравнению с равномерным перекрытием штырей примерно в 1,35 раза при α=8 и в 1,55 раза при α=12.
частотная характеристика не имеет боковых выбросов, а полоса пропускания расширяется по сравнению с равномерным перекрытием штырей примерно в 1,35 раза при α=8 и в 1,55 раза при α=12.
Реально в фильтре с аподизованным преобразователем при перекрытии штырей по закону e![]() будут небольшие выбросы, так как значения перекрытия начинаются скачком не с нуля, а с 5% для α=12 и с 13% для α=8. Таким образом, изменяя закон перекрытия штырей относительно центра преобразователя, можно менять форму частотной характеристики, уменьшая боковые выбросы. Однако, при этом будут меняться ширина полосы.
будут небольшие выбросы, так как значения перекрытия начинаются скачком не с нуля, а с 5% для α=12 и с 13% для α=8. Таким образом, изменяя закон перекрытия штырей относительно центра преобразователя, можно менять форму частотной характеристики, уменьшая боковые выбросы. Однако, при этом будут меняться ширина полосы.

Рис.4.
ЛИТЕРАТУРА
1. Петров К.С. Радиоматериалы, радиокомпоненты и электроника: Учебное пособие для вузов. – СПб: Питер, 2003. – 512 с.
2. Опадчий Ю.Ф. и др. Аналоговая и цифровая электроника: Учебник для вузов / Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров; Под. ред. О.П. Глудкина. М.: Горячая Линия – Телеком, 2002. – 768 с.
3. Акимов Н.Н. и др. Резисторы, конденсаторы, трансформаторы, дроссели, коммутационные устройства РЭА: Справочник / Н.Н. Акимов, Е.П. Ващуков, В.А. Прохоренко, Ю.П. Ходоренок. Мн.: Беларусь, 2005. – 591 с.