| Похожие рефераты | Скачать .docx |
Дипломная работа: Постановка задачи синтеза оптимальных алгоритмов приема сигналов на фоне помех
Содержание
1. Вводные замечания
2. Модели сигналов и помех
3. Вероятностные характеристики случайных процессов
4. Энергетические характеристики случайных процессов
5. Узкополосные случайные процессы
6. Временные характеристики случайных процессов
7. Особенности нестационарных случайных процессов
8. Классификация случайных процессов
Библиографический список
1. Вводные замечания
В процессе приема сигналов на вход приемного устройства поступает либо смесь сигнала и помехи, либо помеха. Оптимальное приемное устройство обнаружения на первичном этапе обработки должно наилучшим образом вынести решение о принятом сигнале, т.е. определить, присутствует или отсутствует сигнал, какой тип сигнала присутствует (на втором этапе обработки), оценить значение того или иного параметра (амплитуды, длительности, времени прихода, направление прихода и т.д.). Сформулированная задача может решаться при априорно неизвестных моделях сигналов и помех, при неизвестных (мешающих) параметрах или неизвестных распределениях сигналов и помех. Основная цель заключается в синтезе оптимальной структуры приемного устройства. Синтезированная структура чаще всего практически нереализуема, однако ее эффективность является потенциальной и дает верхнюю границу эффективности любых практически реализуемых структур.
Синтез оптимальных процедур обработки сигналов и помех может производиться с использованием различных методов оптимизации:
1. Использование корреляционной теории:
а) критерий максимума отношения сигнал/помеха;
б) критерий минимума среднеквадратической ошибки.
2. Использование теории информации для максимизации пропускной способности системы. Главное направление – построение наилучших методов кодирования.
Применение теории статистических решений.
Задача оптимизации может быть решена только при наличии критерия, который задается разработчиком системы.
Чтобы воспользоваться теорией статистических решений при синтезе оптимальных приемных устройств, необходимо иметь математические модели сигналов и помех. Эти модели должны включать описание формы сигнала (если она известна). Статистические характеристики и характер взаимодействия сигнала и помехи вплоть до n-мерных плотностей вероятностей.
Теория статистических решений имеет следующие составные части:
1) теорию проверки статистических гипотез:
а) двухальтернативные задачи обнаружения или распознавания сигналов;
б) многоальтернативные задачи при различении многих сигналов на фоне помех;
2) теорию оценки параметров, если эти параметры составляют счетное множество;
3) теорию оценки процесса, который необходимо выделить из входной смеси с минимальной ошибкой.
Постановка задачи синтеза оптимального приемного устройства и ее решение существенным образом зависят от объема априорных (доопытных) сведений о характеристиках сигналов и помех. По объему априорных данных различают задачи с полной априорной определенностью (детерминированный сигнал и помеха с полностью известными вероятностными характеристиками), с частичной априорной определенностью (имеются известные параметры сигнала и помехи) и с априорной неопределенностью (известны лишь некоторые сведения о классах сигналов и помех) [5]. Следует заметить, что эффективность разработанных обнаружителей и измерителей параметров существенно зависит от объема априорной информации.
Следует заметить, что, если о сигналах и помехах ничего неизвестно (полностью отсутствует информация о них), то такая задача не может быть решена.
2. Модели сигналов и помех
Сигнал – это процесс, служащий для передачи информации или сообщения. Остальные процессы, воспринимаемые приемным устройством вместе с сигналом, являются помехами.
Сигналы классифицируются по объему априорных сведений:
а) детерминированные сигналы (неслучайные);
б) детерминированные по форме сигналы со случайными параметрами (квазислучайные);
в) псевдослучайные, шумоподобные сигналы (они близки по свойствам к случайным процессам, но генерируются детерминированным образом и при воспроизведении полностью повторяются);
г) случайные сигналы.
В зависимости от характера изменения во времени сигналы подразделяются на дискретные и непрерывные. Дискретные сигналы используются в цифровых устройствах, в радиолокации. Непрерывные (континуальные) – в телефонии, радиовещании, телевидении и т.д. В последнее время дискретные сигналы используются и в цифровом телевидении и радиовещании.
Каждый сигнал может быть охарактеризован по степени сложности в зависимости от величины, называемой базой сигнала: B = F∙T, где F – эффективная ширина спектра сигнала; Т – эффективная длительность сигнала. Если B » 1, то сигнал называется простым, при B >> 1 – сложным сигналом. Сложные сигналы получают либо из совокупности простых сигналов, либо с помощью модуляции. К сложным сигналам могут быть отнесены шумовые и шумоподобные сигналы. У таких сигналов ![]() , где Т – эффективная длительность сигнала (когда сигнал эквивалентен по энергии сигналу с прямоугольной формой);
, где Т – эффективная длительность сигнала (когда сигнал эквивалентен по энергии сигналу с прямоугольной формой); ![]() – интервал корреляции процесса.
– интервал корреляции процесса.
В различных системах, как правило, излучают радиосигналы, отличающиеся по виду модуляции: амплитудно-модулированные, частотно-модулированные, фазомодулированные, сигналы с импульсными видами модуляции; манипулированные (по амплитуде, частоте, фазе и совмещенные) сигналы.
В радиолокации чаще всего излучается последовательность радиоимпульсов.
Упрощенная структура РЛС представлена на рис. 1, где использованы следующие обозначения: РПУ – радиопередающее устройство; РПрУ – радиоприемное устройство; АП – антенный переключатель; s0(t) – зондирующий сигнал; s(t) – отраженный сигнал; А – антенна; О – обнаруживаемый объект; V – скорость сканирования антенны. Облучение пространства производится периодическим зондирующим сигналом.
Импульс отражается от объекта обнаружения и возвращается с задержкой к антенне РЛС. Задержка определяется расстоянием между РЛС и объектом. Интенсивность отраженного сигнала зависит от эффективной поверхности рассеяния (ЭПР) объекта и условий распространения радиосигнала. В РЛС одна и та же антенная система используется при передаче и приеме сигналов. Интенсивность облучения объекта зависит от формы диаграммы направленности антенны и угла между направлением на объект и направлением максимального коэффициента направленного действия. При сканировании антенной системы (механическом или электронном вращении диаграммы направленности) огибающая пачки импульсов отраженного сигнала повторяет форму диаграммы направленности (рис. 1). В режиме сопровождения объекта огибающая пачки импульсов может иметь прямоугольную форму.

Рис. 1
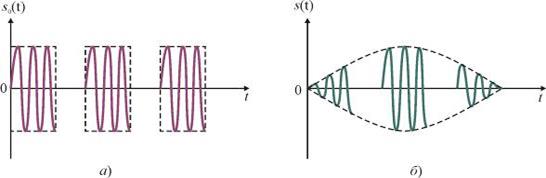
Рис 1
При обзоре время облучения ограничено, и принимаемый сигнал представляет собой ограниченную по времени пачку радиоимпульсов. Модуляция по амплитуде импульсов в пачке определяется не только формой диаграммы направленности, но и скоростью V обзора, от нее зависит и число импульсов в пачке. Обычно огибающая пачки – детерминированная функция, поскольку вид диаграммы направленности и скорость обзора известны.
Запаздывание отраженного сигнала зависит от дальности r до объекта – ![]() , где c – скорость распространения радиоволны в пространстве. При распространении сигнал ослабляется относительно излученного в 106 – 1010 раз по напряжению. Кроме того, изменение угла между направлением максимума диаграммы направленности антенны и объектом и поворот объекта за время облучения приводит к случайным изменениям амплитуды импульсов принимаемого сигнала. За счет радиальной скорости объекта Vr изменяется и частота отраженного сигнала (доплеровский эффект), при этом приращение частоты несущего колебания
, где c – скорость распространения радиоволны в пространстве. При распространении сигнал ослабляется относительно излученного в 106 – 1010 раз по напряжению. Кроме того, изменение угла между направлением максимума диаграммы направленности антенны и объектом и поворот объекта за время облучения приводит к случайным изменениям амплитуды импульсов принимаемого сигнала. За счет радиальной скорости объекта Vr изменяется и частота отраженного сигнала (доплеровский эффект), при этом приращение частоты несущего колебания ![]() . Изменяются параметры сигнала в канале связи и во входных трактах приемной системы.
. Изменяются параметры сигнала в канале связи и во входных трактах приемной системы.
При отражении сигнала от объекта происходит изменение поляризации падающей волны. Эти изменения зависят от формы объекта и могут быть использованы при распознавании объектов.
Построить модель сигнала, которая учитывала бы все эти влияния и изменения сложно, поэтому учитывают только часть рассмотренных изменений.
Основные модели сигналов
а) Детерминированный сигнал:
![]() .
.
Все параметры сигнала: амплитуда А, закон ее изменения во времени S0(t), частота w0 и закон изменения начальной фазы ![]() во времени известны, т.е. огибающая S(t) и фаза
во времени известны, т.е. огибающая S(t) и фаза ![]() являются детерминированными функциями времени.
являются детерминированными функциями времени.
б) Одиночный сигнал со случайной амплитудой и фазой
![]() ,
,
где А, j, t – случайные параметры.
Случайные параметры задаются плотностями вероятности. Распределение амплитуд А чаще всего полагают релеевским
 ,
,
где s2 – дисперсия флюктуаций амплитуды.
Начальная фаза j и задержка t распределены равномерно, т.е.
![]() ,
,
где Т – период зондирования, определяемый максимальной однозначной дальностью действия РЛС.
Функции s0(t) и ![]() – детерминированные.
– детерминированные.
Для движущихся объектов локации к несущей частоте w0 добавляется доплеровский сдвиг ![]() , где
, где ![]() – случайная величина, знак которой зависит от направления перемещения объекта в радиальном направлении относительно РЛС.
– случайная величина, знак которой зависит от направления перемещения объекта в радиальном направлении относительно РЛС.
в) Нефлюктуирующая пачка радиоимпульсов
 ,
,
где ![]() ; функция H2(t) – функция, обусловленная формой диаграммы направленности (рис. 2б); Т0 – период следования импульсов в пачке; К = const.
; функция H2(t) – функция, обусловленная формой диаграммы направленности (рис. 2б); Т0 – период следования импульсов в пачке; К = const.
г) Флюктуирующая пачка импульсов:
– дружно-флюктуирующая пачка – амплитуды радиоимпульсов в пачке неизменны, но изменяются независимо от пачки к пачке, что соответствует медленному изменению ЭПР отражающего объекта во времени или изменению параметров канала распространения электромагнитной волны и т.д. (рис. 2);
– быстро-флюктуирующая пачка – амплитуды радиоимпульсов изменяются в пачке от импульса к импульсу независимо (рис. 3).
В зависимости от характера изменения начальной фазы колебаний от импульса к импульсу в пачке различают когерентные и некогерентные пачки радиоимпульсов. Когерентная пачка может быть образована путем вырезания импульсов из непрерывного стабильного гармонического колебания. Начальные фазы в этом случае или одинаковы во всех радиоимпульсах пачки, или изменяются по известному закону. Некогерентная пачка состоит из радиоимпульсов с независимо-изменяющейся начальной фазой.
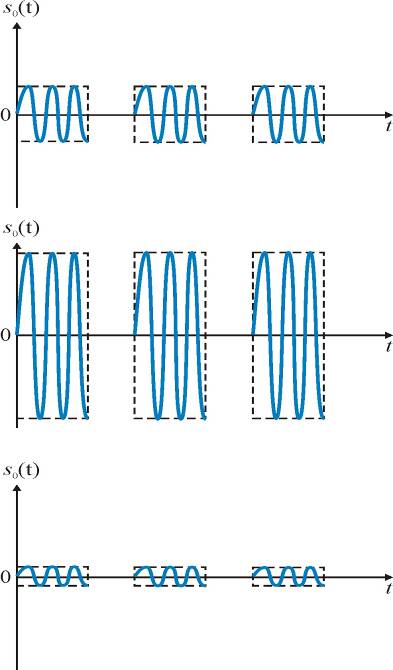
Рис. 2

Рис. 3
Помехи разделяются на естественные (неорганизованные) и искусственные (организованные), внутренние и внешние.
По способу образования помехи могут быть пассивными и активными. Естественные пассивные помехи создаются отражениями от местных предметов (в радиолокации) и земной поверхности, растительности и т.д.; отражениями от метеорных следов и атмосферных неоднородностей (в радиосвязи на УКВ).
Активные помехи имеют самостоятельный источник, в то время как пассивные помехи обусловлены излучением зондирующего сигнала. По характеру изменения во времени помехи бывают флюктуационные (гладкие) и импульсные.
В качестве помех могут быть случайные, шумоподобные или детерминированные процессы. Из всех помех наибольшее воздействие на подавляемую РЛС оказывает белый (широкополосный) шум с нормальным распределением, поскольку он имеет наибольшую информационную емкость.
Чаще всего в качестве моделей помех используется их описание с помощью статистических характеристик. Наиболее полной характеристикой является n-мерная плотность вероятности. Однако в некоторых частных, но очень важных случаях помеха может быть охарактеризована одномерной или двумерной плотностями вероятности.
Сигналы и помехи могут быть представлены в виде некоторых множеств в частотно-временной системе координат (рис. 4).
Каждый сигнал или помехи занимают по осям w и t определенные отрезки, зависящие от полосы частот Dw и длительности t. Чем больше Dw и t, тем эффективнее помеха с точки зрения подавления сигнала. Наилучшей помехой является белый шум, который заполняет всю плоскость w, t, и обладает наибольшими дезинформационными свойствами. Если шум узкополосный, то он занимает ограниченную площадь, поскольку имеет неравномерную спектральную плотность мощности. От такой помехи можно избавиться, перестроив несущую частоту w0 сигнала.
Для пространственно-временных сигналов и помех используются дополнительные координаты: угол места и азимут. И тогда источники помех могут быть точечными по угловым координатам или распределенные в конкретных секторах.

Рис. 4
Геометрическое представление сигналов и помех связано с введением многомерного пространства выборок и широко используется в теории сигналов [7, 8]. Пусть имеется реализация x(t) случайного процесса X(t). В соответствии с теоремой Котельникова эта реализация может быть представлена в виде дискретных отсчетов xi = x(iDt). Число этих отсчетов (единичных измерений) – N, совместно они образуют выборку X размером N – ![]() , i – номер измерения в выборке X. Если представим n-мерное пространство, в котором на каждой оси координат отложим соответствующие по номеру измерения, то вся выборка будет соответствовать точке этого пространства или вектору, конец которого лежит в этой точке. Длина вектора в данном пространстве может быть представлена так:
, i – номер измерения в выборке X. Если представим n-мерное пространство, в котором на каждой оси координат отложим соответствующие по номеру измерения, то вся выборка будет соответствовать точке этого пространства или вектору, конец которого лежит в этой точке. Длина вектора в данном пространстве может быть представлена так:
 .
.
Эта величина называется нормой вектора в эвклидовом пространстве. В пространстве Хемминга норма выражается иначе:
 .
.
Если ![]() и
и ![]() , то в пределе переходим к бесконечному пространству
, то в пределе переходим к бесконечному пространству ![]() , в котором норма определяется так
, в котором норма определяется так
 .
.
Для реальных процессов ![]() и имеет размерность величины x.
и имеет размерность величины x.
Все указанные пространства линейны, и для них определены операции сложения элементов множества и умножения элемента на число. Причем обе эти операции удовлетворяют условиям коммутативности, ассоциативности и дистрибутивности.
Среди линейных пространств можно выделить метрические пространства, для которых существует метрика ![]() , т.е. норма разности векторов, которая больше или равна нулю. Метрика (расстояние) обладает следующими свойствами:
, т.е. норма разности векторов, которая больше или равна нулю. Метрика (расстояние) обладает следующими свойствами:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ,
,
где x, y, z – элементы пространства.
Для эвклидова конечно-мерного пространства ![]() –
–
 ,
,
для непрерывного пространства ![]() аналогично
аналогично
 .
.
Важным является понятие скалярного произведения. Оно характеризует собой проекцию одного вектора на другой и определяется в ![]() так:
так:
 ,
,
т.е. сумма произведений одноименных проекций векторов на оси координат. В непрерывном пространстве ![]() :
:  , причем скалярное произведение
, причем скалярное произведение ![]() всегда не больше произведения норм векторов (неравенство Шварца).
всегда не больше произведения норм векторов (неравенство Шварца).
Угол между векторами определяется так
 .
.
Если определить норму через скалярное произведение, то говорят, что норма порождена скалярным произведением, а пространство, отвечающее такому произведению, называется гильбертовым.
Введем понятие случайного вектора. Случайный вектор – это такой вектор, координаты которого есть случайные величины. Этот вектор ![]() в пространстве выборок не занимает какого-либо фиксированного положения. Его конец может оказаться в той или иной области пространства с известной вероятностью, которую можно подсчитать, зная совместное распределение случайных величин
в пространстве выборок не занимает какого-либо фиксированного положения. Его конец может оказаться в той или иной области пространства с известной вероятностью, которую можно подсчитать, зная совместное распределение случайных величин ![]() . Конец вектора можно представить себе не как определенную точку, а как облако, переменная плотность которого выражает вероятность нахождения конца вектора в данном элементе объема пространства. Геометрически это облако отображается гиперсферой в n-мерном пространстве (рис. 5).
. Конец вектора можно представить себе не как определенную точку, а как облако, переменная плотность которого выражает вероятность нахождения конца вектора в данном элементе объема пространства. Геометрически это облако отображается гиперсферой в n-мерном пространстве (рис. 5).

Рис. 5
Элементарный объем в пространстве выборок ![]() . Вероятность попадания конца вектора в этот объем будет равна
. Вероятность попадания конца вектора в этот объем будет равна
![]() ,
,
где ![]() – плотность вероятности случайного процесса X(t).
– плотность вероятности случайного процесса X(t).
Если гиперсфера имеет размеры W, то попаданию точки в эту гиперсферу соответствует вероятность
![]() ,
,
где ![]() – проекции гиперсферы W на оси координат системы.
– проекции гиперсферы W на оси координат системы.
Это выражением может быть записано в векторной форме
![]() .
.
Если ![]() распределены по нормальному закону с одинаковой дисперсией каждой их независимых компонент, то вероятность попасть в элементарный объем
распределены по нормальному закону с одинаковой дисперсией каждой их независимых компонент, то вероятность попасть в элементарный объем ![]() пространства выборок равна
пространства выборок равна
 ,
,
где  – расстояние от начала системы координат до элемента
– расстояние от начала системы координат до элемента ![]() .
.
В данном случае облако имеет сферическую форму. При различных дисперсиях облако вытягивается вдоль тех осей, которым соответствуют единичные измерения с большей дисперсией.
Если даны два случайных процесса x и h, то косинус угла между их векторами соответствует нормированному коэффициенту взаимной корреляции. Геометрически он характеризует проекцию единичных векторов одного на другой. Если x = h, то ![]() – линейная зависимость, если же они перпендикулярны, то
– линейная зависимость, если же они перпендикулярны, то ![]() – показывает полное отсутствие коррелированности. В этом случае векторы ортогональны, а процессы некоррелированы.
– показывает полное отсутствие коррелированности. В этом случае векторы ортогональны, а процессы некоррелированы.
Для нормальных процессов некоррелированность означает и независимость, поскольку для них иной случайной зависимости, кроме линейной, не существует. Доказывается такое утверждение подстановкой коэффициента корреляции, равного нулю, в двумерную нормальную плотность вероятности. В результате такой подстановки плотность вероятности преобразуется к произведению одномерных плотностей вероятности, что является необходимым и достаточным условием статистической независимости двух случайных величин, входящих в систему.
3. Вероятностные характеристики случайных процессов
1. Наиболее полными вероятностными характеристиками случайных процессов (СП) являются различные виды распределений вероятностей мгновенных значений, среди которых основное применение получили интегральная функция распределения вероятностей и плотность вероятности.
Для ансамбля реализаций СП (рис. 6) одномерная интегральная функция распределения определяется как вероятность того, что мгновенные значения реализаций не превысят некоторый фиксированный уровень x в момент времени t.
Аналогично определяется n-мерная интегральная функция распределения как вероятность совместного выполнения неравенств:
![]() . (1)
. (1)
Виды одномерной интегральной функции распределения для различных процессов показаны на рис. 8.
![]() .
.
В отличие от интегральных функций распределения случайных величин, эта характеристика СП в общем случае (для нестационарных СП) зависит от времени.

Рис. 6
Так же как и для случайных величин, ![]() (положительная определенность),
(положительная определенность), ![]() при x2 > x1 (интегральная функция является неубывающей),
при x2 > x1 (интегральная функция является неубывающей), ![]() (ограниченность).
(ограниченность).

Рис. 7
Хотя интегральная функция распределения вероятности определена и для непрерывных, и для дискретных процессов, большее распространение получила плотность вероятности, определенная только для непрерывных СП.
Одномерная плотность вероятности определяется как производная от интегральной функции по аргументу x:
![]() .
.
Для n-мерной плотности в соответствии с (1) имеем:
 . (2)
. (2)
Из представления производной в виде предела отношения конечных приращений ![]() можно сделать вывод, что плотность вероятности характеризует относительную частоту пребывания мгновенных значений в элементарном интервале Dx.
можно сделать вывод, что плотность вероятности характеризует относительную частоту пребывания мгновенных значений в элементарном интервале Dx.
На рис. 7 приведены графики плотности вероятности для реализаций различной формы.
Аналогичное рассмотрение n-мерной плотности вероятности позволяет интерпретировать ее как вероятность того, что значение функции находятся в пределах n коридоров Dx или, иначе, что реализация примет заданную форму (рис. 8).

Рис. 8
Свойства плотности вероятности:
– положительная определенность – ![]() ;
;
– свойство симметрии – значения плотности вероятности не меняются при перестановке аргументов;
– свойство нормировки  ;
;
– свойство согласованности (число интегралов в правой части равно n – m)

– плотность вероятности меньшего порядка вычисляется путем интегрирования по «лишним» аргументам;
– размерность плотности вероятности обратна размерности случайной величины.
Наиболее широко в радиотехнике используются следующие распределения.
1. Нормальной (гауссово) распределение (рис. 9):

Рис. 9
 ,
,
где m – математическое ожидание; s – среднеквадратическое отклонение (СКО).
Для нормального распределения характерна симметрия относительно математического ожидания и большие значения случайной величины встречаются значительно реже малых:
![]()
![]()
![]() .
.
2. Равномерное распределение (рис. 10):


Рис. 10
Экспоненциальное распределение (рис. 11):


Рис. 11
4. Распределение Рэлея (распределение огибающей узкополосного нормального СП):


Рис. 12
2. Распределения вероятностей, хотя и является наиболее употребимыми в теории характеристиками, не всегда доступны для экспериментального определения и во многих случаях слишком громоздки в теоретических исследованиях. Более простыми являются числовые характеристики СП, определяемые как некоторые функционалы от плотности вероятности. Наиболее широко из них используются моментные функции, определяемые как среднее значение различных степенных преобразований СП.
Начальные одномерные моменты определяются в виде
 . (3)
. (3)
Особое значение имеют первый начальный момент – математическое ожидание  и второй начальный момент
и второй начальный момент
 .
.
сигнал случайный помеха прием
Физический смысл этих характеристик: среднее значение и средняя мощность СП, выделяемая на сопротивлении в 1 Ом, соответственно (если СП есть напряжение, стационарное по постоянной составляющей и мощности). Второй начальный момент характеризует степень разбросанности случайной величины относительно начала координат. Размерность математического ожидания совпадает с размерностью величины x (для x в виде напряжения – вольты), а размерность m2 – с размерностью квадрата величины x.
В случае стационарных СП моменты не зависят от времени, для нестационарных могут быть функциями времени (в зависимости от типа не-стационарности), что поясняется рис. 13.

Рис. 13
Центральные моменты определяются аналогично начальным моментам, но для центрированного процесса ![]() :
:
 . (4)
. (4)
Поэтому всегда ![]() .
.
Второй центральный момент – дисперсия СП – определяется в виде

и характеризует степень разбросанности значений относительно математического ожидания или, иначе, среднюю мощность переменной составляющей процесса, выделяемой на сопротивлении в 1 Ом. Очевидна связь между начальными и центральными моментами:
![]() , в частности
, в частности ![]() .
.
Отметим, что третий центральный момент (p = 3 в (4)) характеризует асимметрию распределения вероятностей (для симметричных плотностей вероятности ![]() ), а четвертый (p = 4) – степень остроты вершины плотности вероятности.
), а четвертый (p = 4) – степень остроты вершины плотности вероятности.
Рассмотрим пример вычисления одномерных моментов распределения.
ПРИМЕР 1. Процесс с треугольной симметричной плотностью вероятности виден на экране осциллографа в виде шумовой дорожки с размахом от -2 до +4 В. При выключенной развертке яркость вертикальной линии в центре экрана равномерна. Оценить математическое ожидание и дисперсию процесса.
Решение примера 1. Сведения о форме распределения и его границах позволяет записать аналитическое выражение для плотности вероятности (рис. 14).
При этом максимальное значение плотности вероятности fm, достигаемое при x=1 В, определяется из условия нормировки, т.е. равенства площади треугольника единице:
 ,
,
откуда ![]() .
.

Рис. 14

Такое симметричное треугольное распределение называют также законом Симпсона.
В соответствии с определениями математическое ожидание и дисперсия равны
 = 1 В;
= 1 В;
 .
.
Однако удобнее вычислить вначале второй начальный момент
 = 7 В2,
= 7 В2,
тогда ![]() = 6 В2.
= 6 В2.
Смешанные начальные моменты определяются соотношением

![]() . (5)
. (5)
Смешанные центральные моменты определяются аналогично, но с заменой x в формуле (5) на центрированное значение ![]() .
.
Ввиду того, что значения x в смешанных моментах определяются в различные моменты времени, появляется возможность оценки статистической взаимозависимости значений процессов, разделенных заданными интервалами. Наиболее важным является простейший из смешанных моментов, отображающий линейную статистическую взаимозависимость и называется корреляционной и ковариационной функцией:
 ;
;
 . (6)
. (6)
Как видно из определения, размерность корреляционной функции определяется размерностью квадрата величины x (для напряжения – В2).
Для стационарного СП корреляционная функция зависит только от разности ![]() :
:
 .
.
Следует заметить, что при t = 0 максимальное значение K(0) = s2.
На рис. 15 приведены примеры реализаций процессов с разными корреляционными функциями.
Кроме функционалов на основе степенных функций (моментов) возможны и другие типы функционалов в качестве статистических характеристик СП. Важнейшим среди них является функционал, основанный на экспоненциальном преобразовании и называемый характеристической функцией
 . (7)
. (7)
Нетрудно заметить, что данное выражение представляет преобразование Фурье от плотности вероятности, отличающееся от обычного лишь знаком в показателе экспоненты.
Поэтому можно записать и обратное преобразование, позволяющее по характеристической функции восстановить плотность вероятности:
 .
.
Соответственно для n-мерного случая имеем
![]()
 . (8)
. (8)

Рис. 15
Основные свойства характеристической функции состоят в следующем:
– свойство нормировки ![]() ;
;
– свойство симметрии ![]() ;
;
– свойство согласованности
![]() ;
;
– определение характеристической функции суммы независимых случайных величин
 .
.
Как видно из анализа перечисленных свойств, различные преобразования характеристической функции проще плотности вероятности. Простая связь также между характеристической функцией и моментами плотности вероятности.
Пользуясь определением характеристической функции (7), продифференцируем ее k раз по аргументу u:
 .
.
Отсюда
 .
.
Можно заметить, что операция дифференцирования намного проще, операция интегрирования при определении моментов плотности вероятности.
ПРИМЕР 2. Может ли существовать процесс с характеристической функцией прямоугольной формы?
Решение примера 2. На рис. 16 представлена характеристическая функция прямоугольной формы (а) и соответствующая ей плотность вероятности (б).

Рис. 16
Так как характеристическая функция является преобразованием Фурье от плотности вероятности, то ее обратное преобразование Фурье должно обладать всеми свойствами плотности вероятности. В данном случае
 .
.
График плотности вероятности представлен на рис. 16б.
Как видно из выражения для f(x) и рисунка, полученная плотность вероятности не удовлетворяет условию положительной определенности (![]() ), следовательно, процесс с заданной характеристической функцией не может существовать.
), следовательно, процесс с заданной характеристической функцией не может существовать.
4. Энергетические характеристики случайных процессов
К энергетическим характеристикам СП относят корреляционную функцию, спектральную плотность мощности и непосредственно связанные с ними параметры СП.
В разделе 2 было дано определение корреляционных функций как смешанных центральных моментов второго порядка соответственно автокорреляционной и взаимнокорреляционной функций, т.е.

 .
.
Основные свойства автокорреляционной функции:
– свойство симметрии ![]() , для стационарных процессов – четность
, для стационарных процессов – четность ![]() ;
;
– свойство ограниченности ![]() , для стационарных процессов
, для стационарных процессов ![]() ;
;
– свойство неограниченного убывания с ростом аргумента (для эргодических процессов) ![]() ;
;
– свойство положительной определенности интеграла
 ;
;
– размерность соответствует квадрату размерности случайного процесса.
Это свойство следует из определения спектральной плотности мощности (для случайных напряжений и тока через сопротивление 1 Ом), которое будет приведено ниже.
Для взаимнокорреляционной функции аналогично можно записать:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Ввиду ограниченности корреляционной функции частот используют нормированные корреляционные функции
 ;
;  ,
,
причем ![]() ;
; ![]() .
.
Для более компактного описания свойств случайного процесса вводят понятие интервала корреляции, определяющего интервал времени, на котором существует связь между значениями процесса.
Основные определения интервала корреляции:
– интегральный (для положительно определенных корреляционных функций)  . Геометрически он характеризует ширину основания прямоугольника, равновеликого по площади функции k(t) при t > 0 (рис. 17а);
. Геометрически он характеризует ширину основания прямоугольника, равновеликого по площади функции k(t) при t > 0 (рис. 17а);
– абсолютный интервал корреляции  (в отличие от предыдущего может использоваться для знакопеременных функций
(в отличие от предыдущего может использоваться для знакопеременных функций ![]() ) (рис. 17б);
) (рис. 17б);
– квадратичный интервал корреляции  ;
;
– максимальный интервал корреляции (на уровне a) (рис. 18)
![]() .
.

Рис. 17

Рис. 18
Обычно уровень a выбирается исходя из рассматриваемой задачи и имеет значения 1/e; 0,1; 9,05; 0,01 и т.д.
Последнее определение не является более произвольным, чем предыдущие, так как выбор конкретного вида функционала протяженности произволен и определяется удобством математического решения конкретной задачи. Практически этот интервал корреляции используется в радиоизмерениях для определения интервала, вне которого случайные величины в сечениях случайного процесса можно считать некоррелированными. Достоверность такого предположения определяется выбором уровня a.
Большое значение в статистической радиотехнике имеют спектральные характеристики СП. При этом используются различные интегральные преобразования процесса вида
 .
.
При исследовании линейных систем с постоянными параметрами особое значение имеет ядро преобразования вида ![]() , так как отклик линейных систем на гармоническое воздействие также является гармоническим.
, так как отклик линейных систем на гармоническое воздействие также является гармоническим.
Преобразование Фурье от k-й реализации СП дает также случайную функцию частоты, зависящую от номера реализации:
 .
.
В условиях реального наблюдения можно получить лишь текущий спектр реализации за интервал наблюдения T
 .
.
Приведенные выражения в существенной степени формальны, так как для многих СП условия применимости преобразования Фурье не выполняются, и интеграл не сходится к какому-либо определенному пределу.
Определим квадрат модуля спектральной плотности k-й реализации
 .
.
Предполагая процесс стационарным и центрированным, заменяя ![]() и производя статистическое усреднение по множеству реализаций, определим:
и производя статистическое усреднение по множеству реализаций, определим:
 .
.
Разделив обе части полученного равенства на T и беря предел ![]() , получим
, получим
 .
.
Поясним физический смысл этой характеристики. Учитывая теорему Релея
 ,
,
определим  ;
;  ;
;
 ;
;
 ;
;  .
.
Таким образом, спектральная плотность мощности или энергетический спектр – это усредненная по всем реализациям функция распределения мощности по частотам.
Следовательно, спектральная плотность мощности и корреляционная функция связаны преобразованием Фурье (теорема Винера – Хинчина):
 (9)
(9)
Полагая t = 0, получим
 .
.
Учитывая свойство четности корреляционной функции, запишем
 ,
,
 .
.
В полученных формулах G(w) определялась для положительных значений круговой частоты w, причем G(w) = G(–w). В отличие от такого «двухстороннего» математического спектра, введем односторонний физический спектр:
![]() .
.
Тогда формулы теоремы Винера – Хинчина примут вид:
 (10)
(10)
Часто используется нормированная спектральная плотность мощности
![]() .
.
Из определения G(w) следуют методы его экспериментального определения (рис. 19). А именно: измеряется квадратичным прибором среднеквадратическое отклонение процесса в узкой полосе (с помощью полосового фильтры с прямоугольной АЧХ), возводится в квадрат, а затем делится на эту полосу Dfэ (полоса такая, что S(f0) » const в пределах Dfэ) (рис. 20).

Рис. 19 Рис. 20
Тогда  .
.
Для одиночного колебательного контура ![]() , где Q – добротность контура, следовательно
, где Q – добротность контура, следовательно
 .
.
Спектральная плотность мощности не отражает фазовой структуры сигнала. Две совершенно разные зависимости могут иметь одинаковую спектральную плотность мощности.
Поскольку G(w) и K(t) связаны преобразованием Фурье, для них справедливы основные теоремы о спектрах.
Ширина спектра определяется так же, как и интервал корреляции.
Эффективная (или неудачное название – энергетическая) ширина спектра
 .
.
Определяют также ширину спектра на уровне a: ![]() .
.
Рассмотрим связь интервала корреляции и ширины спектра.
Так как  , а
, а  , то
, то
 . (11)
. (11)
Таким образом, произведение ![]() – порядка единицы.
– порядка единицы.
Различают широкополосные и узкополосные процессы (рис. 22а и б).

а б
Рис. 22
Для узкополосных процессов ![]() . Поскольку для узкополосных случайных процессов значение спектральной плотности мощности при нулевой частоте всегда равно нулю (или очень близко к нему), то корреляционная функция является всегда знакопеременной и ее площадь равна нулю (из теоремы Винера – Хинчина).
. Поскольку для узкополосных случайных процессов значение спектральной плотности мощности при нулевой частоте всегда равно нулю (или очень близко к нему), то корреляционная функция является всегда знакопеременной и ее площадь равна нулю (из теоремы Винера – Хинчина).
Один из широко распространенных в теории широкополосных процессов – белый шум с равномерным спектром ![]() . Его корреляционная функция равна
. Его корреляционная функция равна
 .
.
Противоположный случай – узкополосный процесс – квазидетерминированный СП с дискретным спектром
![]() ,
,
где x1, x2 – случайные величины, не зависящие от t, ![]() .
.
Функция X(t) представляет собой гармоническое колебание со случайной амплитудой ![]() и фазой
и фазой  , распределение которого не зависит от времени. Этот процесс будет стационарным лишь при
, распределение которого не зависит от времени. Этот процесс будет стационарным лишь при ![]() и при
и при ![]() . Тогда
. Тогда ![]() зависит только от t, причем x1 и x2 некоррелированы.
зависит только от t, причем x1 и x2 некоррелированы.
В этом случае ![]() ;
;

![]() . (рис. 23)
. (рис. 23)
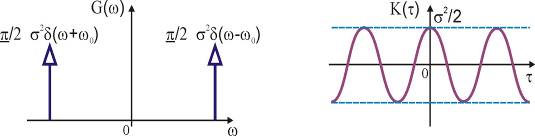
Рис. 23
Для стационарных СП X(t) и Y(t) вводят также взаимную спектральную плотность мощности
![]() ;
;
 ;
;  ;
;
 ;
;  .
.
Взаимная спектральная плотность мощности двух процессов комплексная, если взаимная корреляционная функция нечетная, действительная часть такой спектральной плотности четная, а мнимая – нечетная функция: ![]() .
.
Для суммы стационарных и стационарно-связанных процессов существует соотношение
 .
.
5. Узкополосные случайные процессы
Важность этих процессов для статистической радиотехники требуют более подробного их рассмотрения.
Для более подробного анализа определим огибающую ![]() и фазу
и фазу ![]() узкополосного случайного процесса (УСП). Часто огибающую определяют по формуле
узкополосного случайного процесса (УСП). Часто огибающую определяют по формуле
![]() , (12)
, (12)
где ![]() – сопряженный с
– сопряженный с ![]() по Гильберту процесс. Применяя преобразование Гильберта к исходному выражению для УСП, получаем
по Гильберту процесс. Применяя преобразование Гильберта к исходному выражению для УСП, получаем ![]() . Точность выражения иногда может вызывать сомнение, поскольку только для гармонических колебаний равенство (12) несомненно. Определим, насколько параметры УСП влияют на точность этой формулы.
. Точность выражения иногда может вызывать сомнение, поскольку только для гармонических колебаний равенство (12) несомненно. Определим, насколько параметры УСП влияют на точность этой формулы.
Используя известные соотношения для комплексной амплитуды аналитического сигнала ![]() , получим
, получим
![]() и
и ![]() . (13)
. (13)
Применяя преобразование Гильберта к исходному выражению для УСП и используя составляющие (13) комплексной огибающей, можно записать
 .
.
Разложим функции ![]() и
и ![]() в подынтегральных выражениях в ряд Тейлора в окрестности точки x=t и почленно проинтегрируем. Получим
в подынтегральных выражениях в ряд Тейлора в окрестности точки x=t и почленно проинтегрируем. Получим

 =
=
![]() , (14)
, (14)
где Q(t) – остаточное слагаемое, характеризующее отброшенную часть суммы. Подставив в выражение (14) ![]() и
и ![]() , получим
, получим
![]() . (15)
. (15)
Из формулы (15) видно, что если можно пренебречь функцией Q(t), то сопряженный по Гильберту УСП имеет такую же огибающую, что и исходный УСП.
Из таблиц определенных интегралов известно:


С учетом этих выражений формулу для Q(t) можно записать:


Считаем, что полоса огибающей равна ![]() , поэтому вторые производные по своим значениям не превосходят
, поэтому вторые производные по своим значениям не превосходят ![]() . Поэтому можно полагать, что
. Поэтому можно полагать, что
 .
.
Следовательно:
 .
.
Отсюда видно, что для УСП функции u(t) и u1(t) имеют одинаковую огибающую с погрешностью, зависящей от отношения ширины спектра к его средней частоте. Для узкополосных случайных процессов обязательным является выражение  , следовательно, огибающая удовлетворяет требованиям, которые к ней предъявляются в соответствии с определением УСП, т.е. является касательной в точках, соответствующих максимальным значениям УСП (или вблизи от них), и имеет общие значения с ним в точках касания. Степень «близости» точки касания к максимальному значению зависит от того же отношения
, следовательно, огибающая удовлетворяет требованиям, которые к ней предъявляются в соответствии с определением УСП, т.е. является касательной в точках, соответствующих максимальным значениям УСП (или вблизи от них), и имеет общие значения с ним в точках касания. Степень «близости» точки касания к максимальному значению зависит от того же отношения ![]() .
.
Фаза ![]() однозначно определяется известными соотношениями для представления комплексного числа в показательной форме.
однозначно определяется известными соотношениями для представления комплексного числа в показательной форме.
Графически УСП можно представить в виде вектора, вращающегося с угловой скоростью ![]() , длина вектора медленно меняется во времени так же, как и фазовый угол
, длина вектора медленно меняется во времени так же, как и фазовый угол ![]() . Исходный УСП является проекцией вектора на горизонтальную ось. Если всю систему координат заставить вращаться с той же угловой скоростью, но в противоположном направлении, то та же проекция будет огибающей
. Исходный УСП является проекцией вектора на горизонтальную ось. Если всю систему координат заставить вращаться с той же угловой скоростью, но в противоположном направлении, то та же проекция будет огибающей ![]() .
.
Если исходный УСП является нормальным, то ![]() и
и ![]() также являются нормальными случайными процессами. Если УСП u(t) нормален, стационарен, имеет нулевое среднее значение и функцию корреляции
также являются нормальными случайными процессами. Если УСП u(t) нормален, стационарен, имеет нулевое среднее значение и функцию корреляции ![]() , то
, то ![]() и
и ![]() также имеют нулевые средние значения и корреляционную функцию
также имеют нулевые средние значения и корреляционную функцию ![]() . В то же время
. В то же время ![]() и
и ![]() взаимно некоррелированы, а так как они нормальны, то и взаимно независимы. Сомножитель
взаимно некоррелированы, а так как они нормальны, то и взаимно независимы. Сомножитель ![]() является огибающей корреляционной функции
является огибающей корреляционной функции ![]() .
.
Огибающая и фаза узкополосного случайного процесса. Плотности вероятности огибающей и фазы УСП можно получить, совершая преобразования, которые были использованы для их получения. Эти преобразования показывают, что огибающая и фаза являются независимыми. СВ как в совпадающие, так и в несовпадающие моменты времени. Одномерная плотность вероятности огибающей (в один момент времени) подчиняется закону Рэлея, а плотность вероятности фазы равномерна в пределах от ![]() до
до ![]() .
.
Сложные преобразования показывают, что центрированная корреляционная функция огибающей приближенно равна квадрату огибающей корреляционной функции исходного УСП. Спектральная плотность мощности огибающей имеет два слагаемых: дельта-функцию, соответствующую постоянной составляющей огибающей, и спектральную плотность флюктуационной составляющей, которая является преобразованием Фурье от квадрата огибающей корреляционной функции исходного УСП.
Если СП является суммой узкополосного нормального процесса и синусоиды со случайной начальной фазой, то мгновенные значения синусоиды распределены по закону арксинуса, сумма – по бимодальному закону, соответствующему свертке нормального закона и закона арксинуса. После применения тех же преобразований, что и для узкополосного нормального СП, получим для огибающей распределение Райса
 ,
,
где ![]() , А0 – амплитуда синусоидального сигнала;
, А0 – амплитуда синусоидального сигнала; ![]() – среднеквадратическое отклонение шума.
– среднеквадратическое отклонение шума.
При ![]() распределение Райса переходит в распределение Рэлея.
распределение Райса переходит в распределение Рэлея.
При больших отношениях ![]() , т.е. при А0 >> 1 (отношение сигнал/шум), распределение Райса может быть аппроксимировано нормальным распределением с математическим ожиданием, равным А0.
, т.е. при А0 >> 1 (отношение сигнал/шум), распределение Райса может быть аппроксимировано нормальным распределением с математическим ожиданием, равным А0.
6. Временные характеристики случайных процессов
Во многих случаях, особенно при экспериментальных исследованиях, вместо ансамбля есть лишь одна реализация. Тогда усреднение производится по времени и при некоторых условиях дает результаты, близкие к усреднению по множеству.
Простейший вариант усреднения состоит в определении среднего арифметического значения. Выделим в отрезке реализации СП длительностью T n дискретных отсчетов с интервалом между ними Dt,
![]() (рис. 24).
(рис. 24).
Среднее арифметическое значение определим известным образом:
 .
.
Умножим числитель и знаменатель этого выражения на Dt:
 .
.

Рис. 24
При Dt ® 0 и n ® ¥ сумма перейдет в интеграл, описывающий временное усреднение реализации (обозначается чертой сверху или в данном пособии: ![]() ) или функции от нее:
) или функции от нее:
 . (16)
. (16)
В общем виде можно записать операцию (16) с помощью оператора временного усреднения ST:
![]() .
.
Для того чтобы результат не зависел от длительности отрезка T, возьмем предел при T ® ¥:
 .
.
При экспериментальных исследованиях выполнение условия T ® ¥ невозможно, но достаточно выполнения условия ![]() .
.
Часто начало реализации и начало времени интегрирования не совпадают, поэтому оператор ![]() правильнее записать в виде оператора текущего среднего:
правильнее записать в виде оператора текущего среднего:
 . (17)
. (17)
Используется также симметричная форма этого оператора:
 . (18)
. (18)
Частотные характеристики операторов (4.17) и (4.18) равны соответственно:
![]() ,
, ![]() ,
,
т.е. отличаются лишь фазовым множителем ![]() .
.
Практически часто используется оператор экспоненциального сглаживания, реализуемый с помощью интегрирующей RC-цепи в форме

и имеющий характеристику
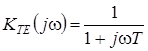 .
.
Производя временное усреднение некоторой функции g[x(t)], лежащей в основе какой-либо вероятностной характеристики, получим соответствующую временную характеристику. В частности, дисперсия, полученная временным усреднением, равна
 ;
;
Временная корреляционная функция –
 .
.
Аналогами распределений вероятностей являются величины относительного времени пребывания реализации ниже некоторого уровня и в интервале уровней (рис. 25).
Аналог интегральной функции распределения вероятностей – относительное время пребывания реализации ниже некоторого уровня (рис. 25а):
 ;
; ![]() .
.
Аналог плотности вероятности – относительное время пребывания реализации в интервале Dx на уровне x (рис. 25б):
 ;
;
 .
.

Рис. 25
Процессы, для которых временные характеристики сходятся в некотором смысле к вероятностным при T ® ¥, называются эргодическими. Различают два вида сходимости.
Последовательность случайных величин ![]() сходится по вероятности к случайной величине x, если для любого e > 0
сходится по вероятности к случайной величине x, если для любого e > 0
![]() .
.
Сходимость с вероятностью 1 (или почти всюду) определяется следующим образом:
![]() .
.
Сходимость в среднем определяется из условия:
![]() ,
,
в частности, сходимость в среднеквадратическом –
![]() .
.
Из сходимости почти всюду следует сходимость по вероятности, а из сходимости в среднеквадратическом также следует сходимость по вероятности.
Часто имеет место не эргодичность процесса, а эргодичность по отношению к математическому ожиданию, корреляционной функции или иной вероятностной характеристике.
7. Особенности нестационарных случайных процессов
Нестационарные СП, в отличие от стационарных, составляют столь широкий класс, что в нем трудно выделить свойства, относящиеся ко всему классу. Одним из таких свойств, лежащих в основе определения нестационарности, является зависимость вероятностных характеристик этих процессов от времени.
В частности,
 ,
,
 .
.
Пример процесса, существенно нестационарного по математическому ожиданию, приведен на рис. 26а, по дисперсии – на рис. 26б.
Нестационарность по математическому ожиданию хорошо описывается моделью аддитивного нестационарного процесса:
X(t) = Y(t) + j(t),
где Y(t) – стационарный СП; j(t) – детерминированная функция.
Нестационарность по дисперсии описывается моделью мультипликативного нестационарного процесса: X(t) = Y(t)·j(t).
Простейшие примеры нестационарности по моментным функциям в более общем виде описываются зависимостями вероятностных распределений от времени.

Рис. 26
Более сложным является отображение нестационарности в рамках многомерных (и даже двумерных) вероятностных характеристик. Наиболее широко используются корреляционные и спектральные характеристики. Поскольку корреляционная функция нестационарного СП зависит от двух моментов времени, спектр нестационарного процесса не может быть определен столь однозначно, как в стационарном случае. Существует несколько определений спектра нестационарных процессов:
а) двойной по частоте спектр или биспектр:
 . (19)
. (19)
В случае стационарного процесса ![]() и соотношение (19) переходит в теорему Винера – Хинчина. Биспектр (19) трудно физически интерпретировать и использовать при анализе цепей, хотя он отображает всю информацию о частотных свойствах процесса;
и соотношение (19) переходит в теорему Винера – Хинчина. Биспектр (19) трудно физически интерпретировать и использовать при анализе цепей, хотя он отображает всю информацию о частотных свойствах процесса;
б) мгновенный частотно-временной спектр.
Заменим в ![]() переменные следующим образом:
переменные следующим образом: ![]() , t = t1 – t2 и выполним преобразование Фурье от корреляционной функции по аргументу t:
, t = t1 – t2 и выполним преобразование Фурье от корреляционной функции по аргументу t:
 . (20)
. (20)
Мгновенный спектр (20) зависит как от частоты, так и от времени и при медленной нестационарности имеет наглядную физическую интерпретацию как изменение «обычной» спектральной плотности мощности во времени (рис. 27);
в) усредненная спектральная плотность мощности
 ,
,
где  .
.
Этот спектр не отображает динамики процесса, но дает представление о среднем распределении дисперсии процесса по частоте;
г) аппаратурный спектр определяется как среднее значение дисперсии процесса на выходе узкополосного фильтра с импульсной реакцией h(t):
 .
.

Рис. 27
Этот спектр допускает аппаратурное определение, но использование его в теории достаточно трудоемко.
ПРИМЕР
Решение примера Рассмотрим пример нестационарного СП, имеющего плотность вероятности, выраженную функцией

где ![]() ; a0 = 1 1/В; k = 2 1/Вс.
; a0 = 1 1/В; k = 2 1/Вс.
Необходимо найти математическое ожидание процесса и нарисовать ориентировочно возможный вид реализации процесса.
Для решения задачи прежде всего определим незаданную функцию А(t) из условия нормировки:
 .
.
Отсюда A(t) = a(t).
Поскольку процесс нестационарный, его математическое ожидание может зависеть от времени и в данном случае равно
 .
.
Учитывая известное значение определенного интеграла [1]
 при
при ![]()
где ![]() – гамма-функция,
– гамма-функция, ![]() , получим
, получим
 .
.
Возможный вид реализаций процесса, не противоречащий виду распределения, приведен на рис. 28.

Рис. 28
На рис. 28 штриховой линией показано изменение математического ожидания процесса.
8. Классификация случайных процессов
Классификация в любой науке служит для упорядочения объектов исследования, а значит, и используемых методов анализа и синтеза. В ряде случаев удачная, логически оправданная и естественная классификация процесса помогает вскрыть новые закономерности (например, периодическая система Менделеева, классификация звезд на основе диаграммы Герцшпрунга – Рассела в астрономии и т.д.).
Классификация производится по каким-либо признакам. Наиболее существенными признаками для СП являются зависимости их вероятностных характеристик от времени и номера реализации.
Обозначим через q(l) произвольную вероятностную характеристику;
![]() – оператор усреднения по множеству;
– оператор усреднения по множеству;
![]() – оператор усреднения по времени.
– оператор усреднения по времени.
Если одновременно используется усреднение и по множеству, и по времени, то получаемая при этом оценка вероятностной характеристики ![]() (l) имеет такой вид:
(l) имеет такой вид:
![]() ,
,
где l – аргумент вероятностной характеристики (частота ![]() в спектральной плотности мощности; интервал
в спектральной плотности мощности; интервал ![]() в корреляционной функции).
в корреляционной функции).
Истинное значение оценки вероятностной характеристики получается с помощью предельного перехода при неограниченном возрастании числа реализаций N и их длительностей T, т.е.
 .
.
Характеристику, полученную усреднением и по множеству, и по времени, будем называть средней вероятностной характеристикой. Если же усреднение производится только по множеству, то получается t – текущая вероятностная характеристика:
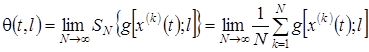 ;
;
только по времени – k-текущая вероятностная характеристика:
 .
.
В зависимости от видов получаемых характеристик СП можно классифицировать таким образом:
– ![]() (k, l) =
(k, l) = ![]() (l) – однородный процесс, т.е. получаемая характеристика не зависит от номера реализации;
(l) – однородный процесс, т.е. получаемая характеристика не зависит от номера реализации;
– ![]() (t, l) =
(t, l) = ![]() (l) – стационарный процесс, т.е. получаемая характеристика не зависит от начала отсчета времени;
(l) – стационарный процесс, т.е. получаемая характеристика не зависит от начала отсчета времени;
– ![]() (t, l) =
(t, l) = ![]() (k, l) =
(k, l) = ![]() (l) – эргодический случайный процесс.
(l) – эргодический случайный процесс.
Схематично процессы могут быть представлены в виде множеств, изображенных на рис. 29.

Рис. 29
Приведенная укрупненная классификация, конечно, не является исчерпывающей, поэтому используется классификация по многим другим признакам.
По виду областей существования и значений случайной функции СП делятся на непрерывные (непрерывные области существования и значений – рис. 30а), дискретные (непрерывное множество значений аргумента и дискретное множество значений – рис. 30б), непрерывные случайные последовательности (дискретная область существования и непрерывная область значений – рис. 30в) и дискретные случайные последовательности (дискретная функция дискретного аргумента – рис. 30г).
По виду распределений вероятностей различают процессы с конечной и бесконечной областями значений, с симметричной и несимметричной плотностью вероятности, гауссовы (нормальные) и негауссовы.

Рис. 30
По корреляционной связи значений различают коррелированные и некоррелированные СП, по виду спектра – широкополосные и узкополосные СП, по характеру временной связи – периодические, непериодические и почти периодические.
По виду нестационарности процессы делятся на аддитивные, мультипликативные, стационарные на интервале (квазистационарные), со стационарными приращениями, периодически нестационарные, с быстрой и медленной нестационарностью и т.д.
Выбор признаков классификации определяется характером решаемой задачи.
Рассмотрим пример классификации СП.
ПРИМЕР 4.
Решение примера 4. Охарактеризовать процесс X(t) в отношении стационарности, однородности и эргодичности, если процесс представлен моделью:
![]() ,
,
где А – случайная амплитуда с рэлеевским распределением; ![]() – случайная величина с равномерным распределением на интервале [–p, p];
– случайная величина с равномерным распределением на интервале [–p, p]; ![]() 0 = const.
0 = const.
Выборочные реализации процесса X(t) представлены на рис. 31.

Рис. 31
Из рис. 31 и аналитического представления квазидетерминированного процесса X(t) очевидно, что его вероятностные характеристики (например, математическое ожидание, дисперсия, плотность вероятности и т.д.) не зависят от времени, т.е. процесс является стационарным. В то же время каждая из реализаций характеризуется своей дисперсией, поэтому процесс неоднороден и не является эргодическим, т.е. его характеристики нельзя оценить по одной реализации.
ПРИМЕР 5. По заданной графически функции распределения ![]() стационарного случайного колебания (рис. 32) определить плотность вероятности и изобразить возможный вид реализации этого процесса.
стационарного случайного колебания (рис. 32) определить плотность вероятности и изобразить возможный вид реализации этого процесса.

Рис. 32
Рассчитать математическое ожидание, второй начальный момент и дисперсию процесса.
Решение примера 5. Плотность вероятности ![]() связана с функцией распределения
связана с функцией распределения ![]() через производную, поэтому на первом участке u от -6 до -3 В производная, характеризующая тангенс угла наклона
через производную, поэтому на первом участке u от -6 до -3 В производная, характеризующая тангенс угла наклона ![]() к оси u равна 0,4/3 = 0,13 1/В. При u = 1 В
к оси u равна 0,4/3 = 0,13 1/В. При u = 1 В ![]() имеет скачок на 0,3, поэтому в плотности вероятности есть d-функция с площадью, равной величине скачка. На участке от 3 до 7 В также
имеет скачок на 0,3, поэтому в плотности вероятности есть d-функция с площадью, равной величине скачка. На участке от 3 до 7 В также ![]() имеет постоянный наклон, равный 0,3/6 = 0,05 1/В. Полученная плотность вероятности представлена на рис. 3 Для проверки вычислений необходимо найти площадь, ограниченную плотностью вероятности (условие нормировки):
имеет постоянный наклон, равный 0,3/6 = 0,05 1/В. Полученная плотность вероятности представлена на рис. 3 Для проверки вычислений необходимо найти площадь, ограниченную плотностью вероятности (условие нормировки): ![]() .
.

Рис. 33
Математическое ожидание равно:
mu =  =
= = –0,325 В.
= –0,325 В.
Второй начальный момент – m2u =  48,9 В2.
48,9 В2.
Дисперсия – ![]() = 48,5 – 0,105625 » 48,4 В2.
= 48,5 – 0,105625 » 48,4 В2.
Реализация длительностью Т, судя по виду плотности вероятности на разных интервалах времени, должна иметь горизонтальные участки на уровне +1 В, суммарная длительность которых должна составлять Т/ На участках от -6 до -3 В и от +1 до +7 В в реализации имеются наклонные прямые линии со случайным наклоном, что соответствует неизменным значениям плотности вероятности. На первом участке мгновенные значения реализации находятся 0,4Т, а на втором – 0,3Т.
Возможный вид реализации представлен на рис. 34.
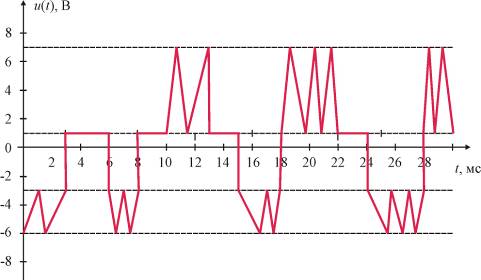
Рис. 34
ПРИМЕР 6. На рис. 35 представлена реализация случайного процесса. Изобразить приближенно плотность вероятности и функцию распределения. Рассчитать (также приближенно) математическое ожидание, среднеквадратическое значение (СКЗ) и среднеквадратическое отклонение (СКО).

Рис. 35
Решение примера 6. Для определения плотности вероятности необходимо в соответствии с ее определением рассчитать вероятности следующих событий:
- соответствия мгновенных значений уровню -10 мА (вероятность р1);
- нахождения мгновенных значений реализации в интервале от -10 до -4 мА (вероятность р2);
- соответствия мгновенных значений уровню -4 мА (вероятность р3);
- нахождения мгновенных значений реализации в интервале от -4 до + 8 мА (вероятность р4);
- соответствия мгновенных значений уровню + мА В (вероятность р5);
- нахождения мгновенных значений реализации в интервале от +8 до +10 мА (вероятность р6).
Для нахождения перечисленных вероятностей необходимо посчитать интервал времени, в течение которого происходили эти события, а затем поделить найденные интервалы на длительность реализации, составляющую 25 мс (см. рис. 35). В результате получим частоты событий (оценку вероятностей). Результаты расчетов представлены в табл. 1.
Таблица 1
| Вероятность |
р1 |
р2 |
р3 |
р4 |
р5 |
р6 |
| Оценка вероятности |
0,04 |
0,18 |
0,2 |
0,36 |
0,1 |
0,12 |
Для расчета значений плотности вероятности в интервалах (-10, -4) мА, (-4, + 8) мА и (+8, +12) мА необходимо полученные вероятности разделить на соответствующие интервалы, предполагая на этих участках постоянную плотность вероятности, так как мгновенные значения в их пределах меняются по линейному закону (рис. 35). Результаты расчетов представлены на рис. 36.
Математическое ожидание равно:

![]() мА
мА
(в предположении стационарности заданного реализацией СП по математическому ожиданию).
Второй начальный момент –
m2i =  36,08 мА2
36,08 мА2
(в предположении стационарности заданного реализацией СП по второму начальному моменту).
Дисперсия –
![]() = 36,08 – 0,1024 » 35,98 мА2
= 36,08 – 0,1024 » 35,98 мА2
(в предположении стационарности заданного реализацией СП по дисперсии).
Следовательно, СКЗ = ![]() » 6,01 мА; СКО =
» 6,01 мА; СКО = ![]() » 6,0 мА.
» 6,0 мА.
Библиографический список
1. Гоноровский, И.С. Радиотехнические цепи и сигналы [Текст] / И.С. Гоноровский. – М. : Радио и связь, 2006. – 608 с.
1. Манжос, В.Н. Теория и техника обработки радиолокационной информа-ции на фоне помех [Текст] / Я.Д. Ширман, В.Н. Манжос. – М. : Радио и связь, 2011. – 416 с.
2. Жовинский, В.Н. Инженерный экспресс-анализ случайных процессов [Текст] / А.Н. Жовинский, В.Н. Жовинский. – М. : Энергия, 2009. – 112 с.
3. Царьков, Н.М. Многоканальные радиолокационные измерители [Текст] / Н.М. Царьков. – М. : Сов. радио, 2010. – 192 с.
2. Математические основы современной радиоэлектроники [Текст] / И.А. Большаков [и др.]. – М. : Сов. радио, 2009. – 208 с.
3. Федосов, В.П. Статистическая радиотехника [Текст] : конспект лекций / В.П. Федосов, В.П. Рыжов. – Таганрог : Изд-во ТРТИ, 2008. – 76 с.
4. Фомичев, К.И. Моноимпульсная радиолокация [Текст] / А.И. Леонов, К.И. Фомичев. – М. : Сов. радио, 2010. – 370 с.
5. Гнеденко, Б.Н. Курс теории вероятности [Текст] / Б.Н. Гнеденко. – М. : Физматгиз, 2011. – 203 с.
Похожие рефераты:
Беспроводные телекоммуникационные системы
Дискретизация и квантование изображений
Техническая диагностика средств вычислительной техники
Математические основы теории систем
Электромагнитная совместимость сотовых сетей связи
Разработка систем передачи информации нового поколения
Теория вероятности и мат статистика
Классификация модемных протоколов