Курсовая работа: Моделирование работы МДП-транзистора в системе MathCad

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Физико-технический факультет

Кафедра полупроводниковой электроники и наноэлектроники

КУРСОВОЙ ПРОЕКТ

по дисциплине: Моделирование физических процессов в микроэлектронике

Тема: Моделирование работы МДП-транзистора в системе Mathcad

Разработал студент гр. ФТ-101Д.М. Жуков

Руководитель А.В. Арсентьев

2010

Содержание

Ведение

1. Полевые транзисторы, их классификация, принцип действия

1.1 Классификация полевых транзисторов

1.2 Принцип действия полевого транзистора с индуцированным каналом

2. Моделирование работы МДП-транзистора

2.1 Теоретическое обоснование компьютерной модели

2.2 Компьютерная модель

Заключение

Список литературы

Введение

В современной цифровой электронике наиболее распространены полевые транзисторы. Это связано с тем, что на полевых транзисторах возможна реализация комплиментарных МОП-структур. Преимущество таких структур в их быстродействии и малой потребляемой мощности. В связи с этим необходимы корректные модели МОП-транзисторов, чтобы было возможно проектирование все более усложняющихся цифровых устройств.

При проектировании схем на полевых транзисторах необходимо знать как выглядит ВАХ транзистора. Этот параметр закладывается в ходе проектирования структуры транзистора. Чтобы предсказать поведение ВАХ нужно знать, какие процессы происходят в структуре при изменении прикладываемых к ней напряжений. Одним из таких процессов, напрямую влияющих на вид ВАХ транзистора, является изменение толщины обедненной области пространственного заряда (ОПЗ) и, следовательно, геометрии канала при изменении напряжения на стоке.

В данной работе будет построена компьютерная модель зависимости толщины ОПЗ от приложенного к току напряжения.

1. Полевые транзисторы, их классификация, принцип действия

1.1 Классификация полевых транзисторов

Полевыми транзисторами называются полупроводниковые приборы (ППП), работа которых основана на модуляции сопротивления слоя полупроводникового материала поперечным электрическим полем.

Протекание электрического тока в полевых транзисторах обусловлено носителями заряда только одного знака (электронами или дырками), поэтому такие транзисторы называют также униполярными в отличие от биполярных.

По физическим эффектам, лежащим в основе управления носителями заряда, полевые транзисторы бывают трех видов: с управляющим p-n-переходом, с управляющим переходом металл полупроводник и со структурой металл–диэлектрик–полупроводник (МДП-транзисторы).

В полевых транзисторах в качестве полупроводникового материала используют в основном кремний и арсенид галлия, в качестве металлов: алюминий, молибден, золото; в качестве диэлектрика оксид кремния SiО₂ в МОП-транзисторах или сложные структуры, например SiO₂ –Al₂ O₃ , SiO₂ –Si₃ N₄ в МДП-транзисторах.

МДП-транзисторы по способу образования канала подразделяются на транзисторы со встроенным каналом (канал создается при изготовлении) и с индуцированным каналом (канал возникает под действием напряжения, приложенного к управляющим электродам). В современных цифровых интегральных схемах (ИС) наиболее распространены МДП-трнзисторы с индуцированным каналом.

По типу проводимости МДП-транзисторы делятся на транзисторы с каналом n-типа и каналом p-типа.

Полевые транзисторы проще биполярных по структуре, кроме того им присущ ряд ценных качеств:

- производство этих приборов проще, они имеют меньшие габариты и можно добиться более высокой степени интеграции ИС;

- потребляемая ими мощность меньше, чем у биполярных транзисторов (мощность, потребляемая МОП - транзисторами, составляет единицы нановатт, в то время как биполярные транзисторы потребляют единицы милливатт);

- применение полевых транзисторов улучшает экономические показатели изделий;

- характерной особенностью полевых транзисторов является высокое входное сопротивление (свыше 10 МОм) и высокий коэффициент усиления по напряжению;

- на базе полевых транзисторов легко создавать запоминающие устройства, работающие за счет накопления зарядов малыми внутренними емкостями;

- надежность полевых транзисторов выше надежности биполярных.

1.2 Принцип действия полевого транзистора с индуцированным каналом

Рассмотрим работу МДП-транзистора с индуцированным каналом p-типа.

Физической основой работы полевого транзистора со структурой металл – диэлектрик – полупроводник (МДП) является эффект поля. Эффект поля состоит в том, что под действием внешнего электрического поля изменяется концентрация свободных носителей заряда в приповерхностной области полупроводника.

В полевых приборах со структурой МДП внешнее поле обусловлено приложенным напряжением на металлический электрод – затвор. В зависимости от знака и величины приложенного напряжения присутствуют четыре состояния области пространственного заряда (ОПЗ) полупроводника – обогащение, обеднение, слабая и сильная инверсия.

Полевые транзисторы в активном режиме могут работать только в области слабой или сильной инверсии, т.е. в том случае, когда инверсионный канал между истоком и стоком отделен от объема подложки слоем обеднения. На рисунке 1 приведена топология МДП - транзистора, где этот факт наглядно виден.

Рисунок 1 – Полевой транзистор со структурой металл – диэлектрик – полупроводник

В отсутствии напряжения, приложенного к структуре ,p-n-переходы, образованные областями стока, истока и подложкой, смещены в обратном направлении. В подложке на границе раздела между полупроводником и диэлектриком образуется отрицательны заряд подвижных электронов, который уравновешивает положительный заряд Q_пов поверхностных состояний. Наличие избыточных электронов у поверхности раздела приводит к искривлению энергетических зон (рисунок 2)

Рисунок 2 – Зонная диаграмма МДП-транзистора в отсутствии внешних электрических полей

Дополнительное искривление зон и накопление отрицательного заряда подвижных электронов у поверхности возникает за счет разности работ выхода для диэлектрика и полупроводника. Чаще всего в качестве диэлектрика используется двуокись кремния SiO₂ . Работа выхода из SiO₂ меньше, чем из кремния, поэтому между диэлектриком и полупроводником возникает контактная разность потенциалов ϕ_МДП , величина которой составляет приблизительно 0,4 В.

Таким образом, в исходном состоянии суммарный отрицательный заряд электронов у поверхности полупроводника обусловлен зарядом поверхностных состояний и разностью работ выхода из полупроводника и диэлектрика. Из условия электронейтральности следует, что суммарный положительный заряд в диэлектрике равен отрицательному заряду подвижных электронов у поверхности полупроводника. Поэтому электрическое поле сосредоточено на границе раздела полупроводника и диэлектрика.

При подаче отрицательного напряжения на затвор, возникающее электрическое поле уменьшает поле, созданное контактной разностью потенциалов и обусловленное Q_пов и приводит к уменьшению заряда подвижных электронов у поверхности. Под действием электрического поля электроны перемещаются вглубь полупроводника. С увеличением отрицательного напряжения на затворе заряд подвижных электронов у поверхности уменьшается и поверхностный слой полупроводника стремится изменить свой тип проводимости с электронного на дырочный. При некотором напряжении на затворе поверхностный слой имеет собственную проводимость. В этом случае уровень Ферми совпадает с серединой запрещенной зоны E_F =E_i (рисунок 3).

Дальнейшее увеличение отрицательного напряжения на затворе приводит к тому, что электроны, связанные с атомами донорной примеси в подложке, отталкиваются в глубь полупроводника, оголяя положительно заряженные ионизированные атомы донорной примеси.

Рисунок 3 – Энергетическая диаграммы МДП-транзистора с E_F =E_i

Неподвижные ионизированные атомы образуют слой объемного заряда, компенсирующийотрицательный заряд на затворе. Толщина слоя объемного заряда с ростом отрицательного напряжения на затворе изменяется незначительно, т.к. за счет увеличения напряженности электрического поля подвижные дырки перемещаются к поверхности и образуют инверсионный слой дырочной проводимости.

Таким образом на поверхности полупроводника индуцируется канал, проводимость которого будет увеличиваться с ростом отрицательного напряжения на затворе.

Под действием разности потенциалов между стоком и истоком в канале транзистора протекает ток стока I_с . При малых отрицательных напряжениях на стоке U_С ток I_с прямо пропорционален приложенному напряжению. Рост U_C , с одной стороны, увеличивает ток стока, т.к. увеличивается электрическое поле вдоль канала, с другой стороны, U_C компенсирует действие напряжения, приложенного к затвору, что приводит к уменьшению толщины канала около стока и его проводимости. Изменение проводимости канала около стока является причиной отклонения зависимости I_C (U_C ) от линейного закона.

Толщина слоя объемного заряда максимальна около стока и минимальна у истока. Дальнейшее увеличение U_C приводит к насыщению тока стока. Когда напряжение на стоке станет равным

, (1.1)

канал в районе стока оказывается перекрытым слоем объемного заряда. Падение напряжения на части канала, свободной от объемного заряда, стабилизируется, а ток I_С насыщается. Длина канала уменьшается на величину Δl (рисунок 4), что уменьшает омическое сопротивление части канала, свободной от объемного заряда, а так как падение напряжения остается равным U_{С ГР} , то ток стока несколько возрастает. Изменение длины канала с ростом U_С является причиной конечной величины выходного сопротивления транзистора. Граничное напряжение U_{С ГР} делит вольтамперные характеристики полевого транзистора на две области: область крутой зависимости тока стока от напряжения на стоке и область пологой зависимости тока от напряжения на стоке.

Крутая и пологая области ВАХ являются рабочими областями МДП-транзистора.

Рисунок 4 – Уменьшение длины канала МДП-транзистора под действием напряжения на стоке

2. Моделирование работы МДП-транзистора

В данной работе будет построена компьютерная модель зависимости геометрии индуцированного канала МДП-транзистора от напряжения приложенного к стоку. Данная модель является полезной при изучении свойств полевого транзистора, т.к. пространственные характеристики канала определяют вид ВАХ прибора.

2.1 Теоретическое обоснование компьютерной модели

Рассмотрим структуру транзистора, показанную на рисунке 5.

Рисунок 5 – Структура транзистора и система координат

В качестве начала отсчета возьмем точку, лежащую на границе раздела диэлектрика и полупроводника, ось y – от истока к стоку вдоль границы раздела. Все напряжения в структуре отсчитываются относительно потенциала истока. При подаче напряжения на затвор U_З в подложке образуется канал толщиной x_К . Канал изолирован от основного объема подложки слоем объемного заряда.

При подаче напряжения на сток транзистора в канале начинает протекать ток. Потенциал на границе канала и слоя объемного заряда изменяется по всей длине канала и является функцией координаты:

, (2)

где U(y) – изменение потенциала на расстоянии y от истока; - потенциал на поверхности слоя объемного заряда, при котором концентрация подвижных дырок в канале преобладает над концентрацией электронов и ионизированных атомов донорной примеси.

Так как все напряжения отсчитываются относительно потенциала истока, то

,

.

Распределение потенциала в слое объемного заряда, обусловленного зарядом ионизированных атомов примеси N_Д , подчиняется уравнению Пуассона. Смещая начало координат в точку x_К , уравнение Пуассона для слоя объемного заряда можно записать в виде

, (3)

где - диэлектрическая проницаемость кремния; - диэлектрическая проницаемость вакуума; q – заряд электрона.

Решим уравнение (3) при граничных условиях

, ,

где h – толщина области объемного заряда; U_п – напряжение, приложенное к подложке.

Решением уравнения является зависимость

,(4)

Толщину слоя объемного заряда h определяем из уравнения (4), подставляя в него значение

.

Тогда

,(5)

Полученное выражение будет использовано в компьютерной модели в качестве основного.

2.2 Компьютерная модель

Модель поведения ОПЗ МДП-транзистора будет построена в системе MathCad.

Для начала построения модели нужно ввести все необходимые исходные данные. Введем сначала физические константы, которые понадобятся нам для дальнейших расчетов. Такими константами являются: заряд электрона, диэлектрическая проницаемость оксида кремния, вакуума и кремния, контактная разность потенциалов между оксидом кремния и кремнием, постоянная Больцмана, концентрация собственных носителей в кремнии, ширина запрещенной зоны кремния. Все эти величины введены в изложенном выше порядке. Часть листинга, соответствующая вводу констант приведена на рисунке 6.

Рисунок 6 – Ввод физических констант

Далее нужно ввести физические параметры самого транзистора. К таковым относятся: концентрация легирующей примеси в подложке Nsub, плотность поверхностных состояний Nss, концентрация примеси в области стока Nd, длина канала W, толщина подзатворного окисла Tox, разность работ выхода из затвора и подложки Ξgsub. Листинг представлен на рисунке 7.

Рисунок 7 – Ввод физических параметров МДП-транзистора

Теперь нужно ввести исходные данные для построения модели. Напряжение на затворе U_g , напряжение на стоке и истоке U_d и U_s , напряжение на подложке U_sub , температура окружающей среды Т.

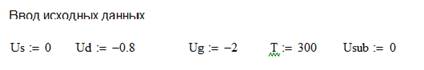
Рисунок 8 – Ввод исходных данных

Теперь, после ввода всех необходимых данных можно приступать к расчетам.

Для начала следует рассчитать пороговое напряжение транзистора. Расчет будем вести по следующей формуле

, (6)

где - потенциал уровня Ферми; - удельная емкость подзатворноко диэлектрика.

В формуле (6) присутствуют величины и , которые тоже необходимо рассчитать.

,

.

Листинг расчета порогового напряжения транзистора представлен на рисунке 9.

Рисунок 9 – Расчет порогового напряжения транзистора

Следует отметить, что MathCad сможет вычислить значение какой-либо величины, в данном случае V_T0 , только в том случае, если все необходимые для расчета величины будут заданы (или вычислены) выше основной расчетной формулы.

Как было сказано в разделе 1.2 настоящей работы, когда напряжение на стоке станет равным , канал в районе стока оказывается перекрытым слоем объемного заряда. Нужно найти это напряжение на стоке. Расчет ведем по формуле (1.1). При дальнейшем увеличении напряжения на стоке наступит момент пробоя p-n-перехода сток-подложка. Это напряжение тоже необходимо посчитать. Расчет пробивного напряжения p-n-перехода будем вести по приближенной формуле

,(7)

Листинг представлен на рисунке 10.

Рисунок 10 – Расчет напряжения перекрытия и пробоя

После расчета напряжений перекрытия канала и пробоя p-n-перехода нужно вычислить величину, на которую уменьшится длина индуцированного канала при превышении напряжением на стоке напряжения перекрытия канала. Листинг расчета представлен на рисунке 11.

Рисунок 11 – Расчет уменьшения длины канала

В приведенном листинге Δl принимает три различных значения. Первое значение определяет величину Δl при напряжениях больших, чем напряжение начала перекрытия канала, но меньших, чем напряжение пробоя p-n-перехода сток-подложка. Второе значение – уменьшение длины канала при напряжениях меньших, чем напряжение перекрытия канала. Очевидно, что это значение ноль. Третье значение Δl – значение при достижении напряжением на стоке величины пробоя p-n-перехода сток-подложка. При этом длина канала перестает уменьшаться.

Толщина ОПЗ зависит от величины потенциала на границе канала и ОПЗ. Вид этой зависимости

,(8)

где – изменение потенциала на расстоянии y от истока.

Примем вид зависимости линейным, т.е. потенциал будет изменяться от истока к стоку как показано на рисунке 12.

Рисунок 12 – Вид зависимости

Исходя из этой зависимости можно, используя теорему Пифагора, найти значение U(y) в каждой точке между истоком и стоком. Листинг расчета представлен на рисунке 13.

Рисунок 13 – Расчет потенциала на границе канала и ОПЗ

Теперь у нас есть все необходимые данные для расчета толщины ОПЗ в зависимости от координаты и напряжении на стоке. Расчет будем вести по формуле (5). Листинг расчета представлен на рисунке 14.

Рисунок 14 – Расчет толщины ОПЗ

В приведенном листинге h(0) – толщина ОПЗ около истока, h(W) и h(W1) – толщина ОПЗ около стока. h(W) – толщина ОПЗ около стока до перекрытия канала, h(W1) – после перекрытия канала. Граница SiO₂ – это граница раздела полпроводника и оксида кремния. Найти границу SiO₂ можно, посчитав толщину ОПЗ при напряжении на стоке равном граничному напряжению перекрытия канала. При этом h(W) и будет границей SiO₂ .

Наглядно поведение толщины ОПЗ можно проследить построив график зависимости h(y). Сначала построим график зависимости h(y) при напряжении на стоке меньше напряжения перекрытия канала (рисунок 15).

Рисунок 15 – Зависимость h(y) при U_C =-0,8 В

Начало координат соответствует истоку транзистора.

Теперь построим ту же зависимость при напряжении на стоке равном напряжению перекрытия (рисунок 16).

Рисунок 16 – Зависимость h(y) при напряжении перекрытия канала

На рисунке 16 видно, что при напряжении на стоке равном напряжению перекрытия канала, толщина ОПЗ около стока становится такой, что ОПЗ касается границы SiO₂ .

При дальнейшем увеличении напряжения на стоке, канал сокращается на величину Δl. Это величина незначительна по сравнению с длиной канала, поэтому на графике при данном масштабе её увидеть невозможно.

Таким образом, меняя значение напряжения на стоке, можно проследить за поведением ОПЗ.

Заключение

транзистор индуцированный напряжение компьютерный

В данной работе была построена компьютерная модель поведения области пространственного заряда МДП-транзистора. С помощью этой модели можно наглядно пронаблюдать изменение геометрии ОПЗ и индуцированного канала транзистора при изменении напряжения на стоке. Эта модель применима для транзисторов с индуцированным каналом любого типа проводимости. Точность модели ограничивается выражением для пробоя p-n-перехода сток-подложка, так как это выражение применимо только для резких переходов без учета их геометрии. Но тем не менее эта модель обеспечивает достаточную точность для инженерных расчетов МДП-транзисторов.

Список литературы

1. Валиев К.А. Цифровые интегральные схемы на МДП-транзисторах/ Карамзинский А.И., Королев М.А. – Советское радио, 1971. – 384 с.

2. Бочаров Л.Н. Полевые транзисторы / Л.Н. Бочаров – М.: Энергия, 1976. – 80 с.

3. Зи С. Физика полупроводниковых приборов: В 2-х книгах. Кн. 1. Пер. с англ. – 2-е перераб. И доп. изд. – М.: Мир, 1984. – 456 с.

4. Свистова Т.В. Твердотельная электроника: учеб. пособие/ Т.В. Свистова. Воронеж: ГОУВПО "Воронежский государственный технический университет", 2006. Ч. 2. 173 с.

5. Бордаков Е.В. Методические указания к выполнения лабораторных работ по дисциплине «Проектирование и конструирование полупроводниковых приборов и интегральных схем» / Бордаков Е.В., Пантелеев В.И. – Воронеж, ВГТУ, 2005. – 45с.