| Скачать .docx |
Дипломная работа: Система сканирования и стабилизации изображения
Дипломная работа
На тему:
"Система сканирования и стабилизации изображения"
Содержание
Введение
1. Постановка задачи
1.1 Общая формулировка задачи
1.2 Системы координат самолёта
1.2.1 Географическая система координат
1.2.2 Система координат центра масс самолёта
1.2.3 Самолётная система координат
1.2.4 Взаимосвязь различных систем
2. Математическая модель
2.1 Функционирование системы
2.1.1 Измерители угловой скорости
2.1.2 Датчики угла
2.1.3 Двигатели
2.2 Моделирование работы системы
3. Алгоритм управления по одной оси
3.1 Алгоритм управления по одной оси
3.1.1 Алгоритм стабилизации при наведении на определённую цель
3.1.2 Алгоритм стабилизации при сканировании
3.2 Реализация алгоритма
Заключение
Приложение
Список использованной литературы
аэрофотосьемка изображение сканирование стабилизация
Введение
Аэрофотосъёмка — фотографирование территории с высоты от сотен метров до десятков километров при помощи аэрофотоаппарата, установленного на атмосферном летательном аппарате (самолёте, вертолёте, дирижабле и пр. или их беспилотном аналоге).
Аэрофотоаппара́т (АФА) — специализированный оптико-механический прибор для аэрофотосъёмки, установленный на атмосферном летательном аппарате.
Особенности АФА
Значительное удаление от объектов съёмки, зачастую низкая температура окружающей среды и высокая влажность (из-за высоты съёмки), сильные динамические механические нагрузки (вследствие полёта), быстрая смена объектов съёмки —снимаемой территории —накладывают отпечаток на особенности аэрофотоаппаратов: большой формат кадра, высокая скорость съёмки (скорость работы затвора и перемотки фотоплёнки в плёночных аппаратах), наличие аммортизирующего механизма или пространственно стабилизированной платформы (например, гироплатформы), большое фокусное расстояние объектива и большая светосила, высокая геометрическая точность объектива, работа в автоматическом режиме по программе, задаваемой с командного пульта, а в последнее время и наличие комплекса спутникового позиционирования для определения координат центров проектирования.
Первый в мире АФА для маршрутной и площадной съёмки с самолёта был изобретён русским военным инженером В. Ф. Потте. Фотоаппарат полковника Поте В. Ф. был создан специально для съемки с самолёта. Его испытания прошли летом 1911 г. на Гатчинском аэродроме. Это был первый в мире полуавтоматический плёночный аэрофотоаппарат с однодисковым затвором. Цикл работы аэрофотоаппарата осуществлялся автоматически. Съёмка проводилась на катушечную фотопленку с форматом кадра 13 х 18 см. Объектив имел фокусное расстояние 21 см и относительное отверстие 1:4,5. Во время Первой мировой войны аэрофотоаппарат использовался для разведывательных аэрофотосъёмок. Конструкция фотоаппарата Потте в то время была лучшей в мире. Он использовался в нашей стране до конца 1920-х годов. Им были выполнены первые производственные аэрофотосъёмки с целью создания топографических карт.
Полученные при аэрофотосъемке снимки особенно применимы в картографии, определении границ землевладений, видовой разведке, археологии, изучении окружающей среды, производстве кинофильмов и рекламных роликов и др.
Аэрофотосъемка имеет несколько важных возможностей для съемки заданной местности. Плоскость аэрофотоаппарата может занимать горизонтальное или наклонное положения. Эти аэрофотосъемки называются плановыми и перспективными соответственно. Так же возможно фотографирование на цилиндрическую поверхность или вращающимся объективом. Такая съемка называется панорамной.
В основном, аэрофотосъемка выполняется однообъективным фотоаппаратом, но если требуется увеличить площадь снимка, используются многообъективные аэрофотоаппараты.
Фотографирование могут производить одиночными аэроснимками, по определённому направлению или по площади. Последние названны маршрутными и площадными аэрофотосъеками соответственно.
Для корректного прокладывания маршрута при аэрофотосъемке часть участка местности, сфотографированного на одном снимке, обязательно должна быть фотографированна и на другом. Эту особенность аэрофотоснимков называют продольным перекрытием. Продольное перекрытие - это отношение площади, сфотографированной на двух соседних снимках, к площади, изображенной на каждом отдельном снимке, выраженное в процентах. Обычно значение продольного перекрытия на аэрофотоснимках составляет 60%, хотя в особенных случаях данные значения могут быть изменены в соответствиями с требованиями к этим снимкам.
Если требуется провести аэрофотосъемку обширного по ширине участка, то фотографирование заданной площади производят серией параллельных маршрутов, также имеющих между собой поперечное перекрытие. В данной фотосъемке стандартное значение перекрытия обычно составляет 30%.
Для проведения аэрофотосъемки задается высота полёта относительно фотографируемой местности, фокусное расстояние камеры аэрофотоаппарата, сезон, время и порядок прокладывания маршрутов.
1. Постановка задачи
1.1 Общая формулировка задачи
СПСИ – система приводов стабилизации изображения, используемая на самолёте при сканировании поверхности Земли. В данной дипломной работе будет описано устройство данной системы, составлена математическая модель.
Задачей данного дипломного проекта является разработка алгоритма стабилизации изображения по одной оси при сканировании изображения по этой оси. А также программная реализация данного алгоритма на языке С++.
1.2 Системы координат самолёта
1.2.1 Географическая система координат
Земная базовая систем координат Og Xg0 Yg0 Zg0 . Эта система координат ориентирована по основным направлениям на поверхности Земли. Начало систем Og координат фиксировано и связано с некоторой точкой на поверхности Земли, принадлежащей маршрутной траектории самолёта. Ось Og Xg0 расположена в плоскости горизонта и всегда направлена на Север. Ось Og Yg0 перпендикулярна оси Og Xg0 и направлена по вертикали места вверх. Ось Og Zg0 перпендикулярна плоскости Og Xg0 Yg0 и ее положительное направление выбирается таким образом, чтобы система координат была правой. Эта система координат используется при анализе траекторий движения центра масс самолёта.
1.2.2 Система координат центра масс самолёта
Вторая координатная система OXg Yg Zg - полусвязанная неподвижная система координат. Она характеризуется тем, что ее начало всегда совмещено с центром масс самолёта и перемещается с ним в пространстве. Оси полусвязанной неподвижной системы координат при произвольном движении самолёта всегда остаются параллельными сами себе. Координатные оси полусвязанной системы координат либо параллельны соответствующим осям базовой системы координат так, как показано на рис. 1, либо повернуты в горизонтальной плоскости на постоянный угол курса самолёта.
1.2.3 Самолётная система координат
Третья координатная система OXYZ, используемая при математическом описании движения самолёта, полностью связана с его корпусом, перемещается и вращается вместе с ним. Поэтому такая система получила название подвижной или связанной системы координат. Начало 0 связанной системы осей координат помещено в центр масс (ц.м.) самолета, ось 0X направлена от хвостовой к носовой части самолета, ось 0Y перпендикулярна оси 0X и направлена вверх в плоскости симметрии, ось 0Z перпендикулярна плоскости симметрии самолета и направлена в сторону правой консоли крыла.

Рис.2.1 Связанная система координат самолёта
Ориентация связанной системы координат относительно полусвязанной неподвижной системы координат определяется тремя углами Эйлера: угол рысканья ψ; угол тангажа θ; угол крена γ.
Углом рыскания ψ называется угол между осью OXg и проекцией оси OX связанной системы координат на горизонтальную плоскость OXg Zg .
Углом тангажа θ называется угол между горизонтальной плоскостью OXg Zg и продольной осью OX самолёта.
Углом крена γ называется угол между вертикальной плоскостью OXg Yg и диаметральной плоскостью самолёта OXY.

Рис.2.2 Углы рыскания, тангажа и крена самолёта
1.2.4 Взаимосвязь различных систем

Рис.2.3 Схема, поясняющая взаимодействие трех систем координат: географической, центра масс самолета и самолетной
Заданную угловую ориентацию самолёта относительно осей полусвязанной неподвижной системы координат можно получить, выполнив три последовательных поворота, которые следует проводить в предположении, что в начальный момент углового движения самолёта координатные оси OXg Yg Zg и OXYZ совпадают.
Первый поворот на угол ψ осуществим относительно оси OYg (в начальный момент времени с ней совпадает ось OY). При этом оси OX и OZ, оставаясь в плоскости OXg Zg , займут некоторое промежуточное положение OX' и OZ'.
Пусть ![]() - направляющие орты полусвязанной неподвижной системы координат OXg
Yg
Zg
;
- направляющие орты полусвязанной неподвижной системы координат OXg
Yg
Zg
; ![]() - направляющие орты промежуточной системы координат OX'Yg
Z'.
- направляющие орты промежуточной системы координат OX'Yg
Z'.
Направляющие орты ![]() связаны с ортами
связаны с ортами ![]() следующими соотношениями:
следующими соотношениями:
 (1)
(1)
Это координатное преобразование задается с помощью так называемой матрицы направляющих косинусов, которая в данном случае имеет вид
 (2)
(2)
Другая (векторно-матричная) форма записи системы равенств(1)
 . .
. .
Второй поворот осей координат произведем относительно оси OZ' на угол θ. В результате чего координатные оси OX' и OYg
займут положение OX'' и OY''. Направляющие орты ![]() второй промежуточной системы координат OX''Y''Z' связаны с ортами
второй промежуточной системы координат OX''Y''Z' связаны с ортами ![]() следующими равенствами
следующими равенствами
 (3)
(3)
Здесь матрица направляющих косинусов имеет вид
 (4)
(4)
и тогда уравнения (3) можно переписать в векторно - матричной форме

Третий поворот координатных осей осуществим относительно оси OX'' на угол γ. При этом ось OY'' займет положение OY, а ось OZ' - OZ, ось OX'' совпадет с осью OX. Орты ![]() связанной системы координат определяются через орты промежуточной системы координат OX''Y''Z' с помощью равенств
связанной системы координат определяются через орты промежуточной системы координат OX''Y''Z' с помощью равенств
 (5)
(5)
Матрица направляющих косинусов третьего поворота координатной системы в соответствии с (5) будет
 (6)
(6)
а уравнения (5) в векторно - матричной форме записи перепишутся следующим образом
 .
.
С учетом полученных выше равенств последовательно получаем,
![]()

где ![]() - это матрица преобразований векторных величин, заданных в полусвязанной неподвижной системе координат OXg
Yg
Zg
, в векторные величины в связанной системе координат OXYZ. Непосредственное вычисление матрицы Aдает следующий результат
- это матрица преобразований векторных величин, заданных в полусвязанной неподвижной системе координат OXg
Yg
Zg
, в векторные величины в связанной системе координат OXYZ. Непосредственное вычисление матрицы Aдает следующий результат

Здесь следует отметить, что матрица Aявляется ортогональной, т. е. ![]() .
.
2. Математическая модель
2.1 Функционирование системы
СПСИ – система приводов стабилизации изображения. Ниже на рисунке приведена схема данной системы.

Рис 3.1.1 Схема СПСИ.
С помощью зеркала и объектива происходит сканирование поверхности Земли cсамолета во время полёта. При сканировании зеркало вращается с некоторой угловой скоростью между заданными углами, а с помощью объектива происходит фиксирование изображения.
При этом во время полёта самолёт неустойчив и происходят колебания относительно осей вращения. Углы рыскания, тангажа и крена постоянно меняются. Поэтому для получения правильного изображения необходимо также изменять положение зеркала. Для этого имеются специальные приводы по разным осям зеркала. Они вращаются с помощью двигателей ДБМ. Информацию о необходимом угле поворота по данной оси получают с помощью датчиков угловой скорости – ДУС, а также с помощью датчиков угла – ДУ.
ОЭП-ЛМД – фотоприёмник.
Все устройства связаны по интерфейсу RS-485.
Рис 3.1.2 Схема подключения по RS-485.
2.1.1 Измерители угловой скорости
Датчик ТИУС700 содержит в себе источник света (суперлюминесцентный диод СЛД), деполяризатор, три фото- приемных устройства (УФП), волоконные разветвители (1:1 и 1:2), разделяющие излучение на три канала, три кольцевых интерферометра Саньяка, чувствительных к трем ортогональным осям, и блока электроники, предназначенного для управления режимом работы СЛД, обработки сигналов с фотодетектора, управления фазовым модулятором и передачи информации о величине угловой скорости по интерфейсу RS-485. Кольцевой интерферометр Саньяка состоит из многофункционального интегрально-оптического элемента (МИОЭ) и волоконного контура.
В ТИУС используется один излучатель на три волоконных контура. Использование трех УФП позволяет вести непрерывную обработку сигнала с трех каналов независимыми блоками цифровой обработки (БЦО). Каждый из БЦО формирует напряжения для получения пилообразной компенсирующей ступенчатой модуляции света для компенсации разности фаз Саньяка и для внесения постоянного фазового сдвига между встречными световыми волнами на π/2 рад, с помощью вспомогательной фазовой модуляции.
Аналоговый сигнал о наличии угловой скорости (сигнал рассогласования) с УФП поступает на аналогово-цифровой преобразователь АЦП. Высокоскоростной АЦП под управлением цифрового автомата, реализованного на ПЛИС, преобразует аналоговый сигнал в цифровой и передает в ПЛИС. В ПЛИС цифровой сигнал с АЦП демодулируется и полученный цифровой код со знаком, соответствующий знаку сигнала рассогласования, поступает на цифровой интегратор. Код с итегратора используется для получения наклона фазовой «пилы», соответствующего скорости вращения. Преобразованный в цифро-аналоговом преобразователе (ЦАП) сигнал в виде ступенчатого пилообразного напряжения поступает на МИОЭ. Контур обратной связи замыкается с помощью пилообразной фазовой модуляции. Амплитуда фазовой модуляции автоматически поддерживается у значения ![]() рад. В этом случае, как известно, разность фаз Саньяка компенсируется сигналом с частотой f, определяемой соотношением:
рад. В этом случае, как известно, разность фаз Саньяка компенсируется сигналом с частотой f, определяемой соотношением:
![]() ,
,
где Ω - скорость вращения, D- диаметр ВК, n– эффективный показатель преломления моды в волокне, λ – длина волны в вакууме.
В приборе используются два способа определения скорости вращения.
В первом способе происходит непосредственное измерение частоты следования спадов «пилы». При этом, появление каждого спада соответствует приращению угла поворота канала ТИУС вокруг оси, перпендикулярной ВК, на ![]() /
/![]() рад.
рад.
Для увеличения разрешающей способности прибора применяется способ измерения скорости вращения по наклону фазовой «пилы». Этот способ реализован для исполнения приборов с интерфейсом RS-485.
2.1.2 Датчики угла
Принцип работы преобразователей угловых перемещений основан на регистрации относительной величины прошедшего через растровое сопряжение потока оптического излучения как координатной-периодической функции взаимного углового положения регулярного растра шкалы и растров окон анализатора.
Преобразователь имеет два кинематически связанных функциональных звена: радиальную растровую шкалу 1, жестко связанную с валом преобразователя, и растровый анализатор 2 неподвижного считывающего узла. Радиальная растровая шкала (далее везде лимб) содержит две концентрические информационные дорожки: регулярного растра и референтной метки Б.
Растровый анализатор содержит окна инкрементного считывания и референтную метку Д. Окна позиционно согласованы с дорожкой регулярного растра лимба и имеют внутри растры A, А, B, В с шагом, равным шагу регулярного растра лимба. При этом, в каждой паре окон растры смещены друг относительно друга на величину равную половине их шага, а взаимный пространственный сдвиг растров между парами окон составляет четверть шага растров. Последовательно с растровыми окнами расположено прозрачное окно Г. Референтная метка Д позиционно согласована с дорожкой референтных меток лимба. Считывающий узел решает задачу реализации оптических растровых и кодовых сопряжений, информативно соответствующих величине углового перемещения, и задачу считывания, обработки и анализа текущих значений оптически информативных параметров указанных сопряжений.

Рис

Рис
Конструктивно эти задачи решает инкрементный узел преобразователя перемещений. Первую из них решает механическая часть этого узла, обеспечивая необходимую точность растрового сопряжения лимба и анализатора, а также сносность последних по отношению к оси вращения вала. Вторую - реализуют осветители, фотоприемники и плата электрической схемы выделения и обработки информации о перемещении. Излучающий диод 3, конденсор 7, формирующий параллельный пучок лучей осветителя, окна А, А, В, В анализатора и фотоприемник 6 образуют так называемый канал считывания. Требование повышенной точности преобразователей перемещений диктует применение двух или четырех диаметрально расположенных каналов считывания.
2.1.3 Двигатели
Двигатель ДБМ (Двигатель Бесконтактный Моментный) изначально проектировался для создания на их основе малогабаритных безредукторных систем. Конструктивно двигатель ДБМ представляет собой электрическую машину встраиваемого типа (поставляется в виде двух отдельных компонентов - статора и ротора). При этом необходимое взаимное положение и крепление статора и ротора должно обеспечиваться конструкцией механизма, в который встраивается двигатель. По типу электрической машины двигатель ДБМ относится к классу вентильных электродвигателей.
Электропривод серии ЭДБМ представляет собой функционально завершенное устройство, интегрированное в единую конструкцию, включающее в себя электродвигатель встраиваемого (ДБМ), систему управления и датчик положения ротора.


Рис.1Вид электропривода со стороны блока управления. Рис.2. Вид электропривода со стороны двигателя
Электропривод имеет сквозное осевое отверстие, что позволяет применять его в конструкциях с проходным валом. Небольшой размер в осевом направлении позволяет легко встраивать электропривод в различные устройства и агрегаты.
2.2 Моделирование работы системы
Рассмотрим более подробно работу данной системы.
Сигналы управления приводами вырабатываются пошагово: шаги задаются моментами приема информации, поступающей с периодом 12.8 мс.
Вся активная работа приводов разделяется на отдельные фазы, из них выделяется фаза сканирования, остальные фазы относятся к вспомогательному движению. Длительность всех фаз занимает целое число шагов.
Вначале работы система ожидает сигнал - "начало шага".
Когда сигнал "начало шага" принят, то осуществляется прием и преобразование данных, необходимых на каждом шаге. К этой информации относятся: - угол крена, угол тангажа, угол рыскания, высота полёта, скорость самолёта. Период приёма этой информации 12.8 мс – этим определяется длина шага.
Затем происходит приём следующих данных – параметр перекрытия, угол захвата – угловой размер снимаемой полосы.
После этого производится планирование съемки. Определяются основные опорные точки:
1) Начальное положение;
2) Стартовая точка;
3) Начало сканирования;
4) Конец сканирования.
Вся активная работа приводов разделена на следующие фазы:
1) Начальная установка (setup, движение ОЭП (изображения) из произвольного положения в точку старта, которая несколько отличается от точки – начало сканирования);
2) Топтание на месте (marktime, ожидание начала съёмки в точке старта);
3) Разгон (start, движение ОЭП из точки старта в точку – начало сканирования, осуществляется при подаче сигнала “Съемка”);
4) Сканирование (scan, движение ОЭП из точки – начало сканирования в точку - конец сканирования);
5) Реверс (revers, движение ОЭП из точки – конец сканирования в точку - начало сканирования);
6) Возвращение в исходное состояние (reset, движение ОЭП из точки – конец сканирования в точку начального положения).
Для каждой фазы движения приводов (кроме фазы Топтание на месте) рассчитывается ее продолжительность в виде числа шагов отводимых на ее выполнение:
1) N_setup;
2) N_start;
3) N_scan;
4) N_revers;
5) N_reset.
По окончании планирования начинается фаза - “начальная установка”.
Принимаются и преобразуются данные с датчиков угловой скорости и с датчиков углового положения.
По данным, полученным ранее, и по датчикам угловой скорости аппарата пошагово вычисляются матрицы поворота горизонтальная система координат <-> связанная система координат.
В течение N_setup шагов происходит движение изображения ОЭП из исходного положения в стартовое положение:
Следующей устанавливается фаза “топтание на месте”. В течение неопределенного количества шагов, пока не получен сигнал "Съемка", производится удержание изображения ОЭП в стартовом положении, не смотря на возмущение.
При получении сигнала "Съемка" начинается фаза “разгон”. В течение N_startшагов приводы разгоняются из стартового положения до положения - начало сканирования.
Следующая фаза – фаза “сканирование”, в течение N_scanшагов осуществляется сканирование:
После сканирование, если сигнал "Съемка" есть, то начинается следующая фаза - “реверс”. В течение N_reversшагов приводы совершают реверсивное движение до положения - начало сканирования, - и опять начинается фаза сканирования.
Если же после сканирования сигнал "Съемка" отсутствует, то начинается фаза “возвращение”. В течение N_reset шагов приводы возвращают изображение ОЭП в начальное положение.
Теперь опишем принцип управления приводом:
1. Сигналы управления приводом.
На вход контроллера периодически (с периодом dT = 12.8 мс) подаём рассчитанные нами:
- значения углов поворота ротора UA(n) в радианах;
- значения угловой скорости UW(n).
2. Контроллер работает с тактом, имеющим период dt = 1 мс. На каждом такте – i, ![]() , где
, где ![]() (ceil(x) – наименьшее целое число, не меньшее x), контроллер пересчитывает воздействия по формулам:
(ceil(x) – наименьшее целое число, не меньшее x), контроллер пересчитывает воздействия по формулам:

То есть контроллер экстраполирует полученные значения на весь интервал до получения следующего значения.
3. Контроллеру доступны квантованные данные датчика угла поворота ротора – qA(i).
4. Каждый такт i контроллер вычисляет сигнал управления приводом
 ,
,
(m=2,…,10).
Здесь Ka и Kw коэффициенты. Воздействие вычисляется как функция от разности реального и требуемого угла поворота ротора и разности реальной и требуемой угловых скоростей.
5. Модель управления приводом имеет вид:

где A(i) – истинный угол поворота ротора;
W(i) – истинная угловая скорость.
То есть угловая скорость и угол корректируются с учётом отличия от требуемого значения.
Теперь продемонстрируем графически сканирование.
Пусть нужно совершить два скана. На рисунке 3.2.1 изображён график требуемого углового движения ротора относительно Земли. На графике разными цветами: синим и красным отделены этапы работы привода. Сначала начальная установка, затем разгон, затем сканирование, реверс, второе сканирование и возвращение в исходное состояние.

Рис 3.2.1 График углового движения ротора относительно Земли
Нам необходимо, чтобы на этапе сканирования график изменения угла был линейным угол изменялся от -0.3 радиан до 0.3 радиан за 10 секунд. То есть ![]() .
.
Будем считать, что на остальных фазах изменение квадратичное. При начальной установке: ![]()
![]() , т.к. при t = 0 угол равен нулю, то С1
= 0.
, т.к. при t = 0 угол равен нулю, то С1
= 0.
При разгоне: ![]() .
.
При реверсе: ![]() .
.
При возвращении в исходной состояние: ![]() .
.
В итоге нам нужно найти 11 неизвестных коэффициентов для построения графиков. Фаза начальной установки длится с 0 по 1 секунды. Затем с 1 по 2 секунды разгон; со 2 по 12-ю и с 16 по 26-ю секунды идёт сканирование; с 12-й по 16-ю идёт реверс. И с 26-й по 27-ю секнды. Возвращение в исходное состояние. Найдём коэффициенты из условий:

При начале сканировании должна быть уже достигнута угловая скорость, с которой производится сканирование, поэтому производные угла в конце фазы реверса и разгона должны быть равны производной угла во время сканирования, то есть 0.06.
Составим систему уравнений из этих условий:

Из уравнения находим коэффициенты и строим данный график.

Рис 3.2.2 График угловых колебаний платформы относительно Земли
На рисунке 3.2.2 показан график изменения угла платформы относительно Земли. Этот график моделирует колебания самолёта во время полёта. На нём также выделены этапы работы.
Этот график является случайным, его будем строить как произведение функции косинуса на степенную функцию со случайными коэффициентами.
Рис 3.2.3 График углового движения ротора относительно платформы
На последнем рисунке 3.2.3 показан график углового движения ротора относительно платформы. Система стабилизации скомпенсировала колебания платформы, чтобы выполнялось требуемое движение ротора относительно Земли. График является разностью между первым и вторым графиком.
Приведём код вычисления значений первого и второго графиков:
A = [1 1 0 0 0 0 0 0 0 0 0;
2 1 0 0 0 0 0 0 0 0 0;
0 0 1 1 1 0 0 0 0 0 0;
0 0 4 2 1 0 0 0 0 0 0;
0 0 4 1 0 0 0 0 0 0 0;
0 0 0 0 0 144 12 1 0 0 0;
0 0 0 0 0 256 16 1 0 0 0;
0 0 0 0 0 32 1 0 0 0 0;
0 0 0 0 0 0 0 0 676 26 1;
0 0 0 0 0 0 0 0 54 1 0;
0 0 0 0 0 0 0 0 729 27 1];
b = [-0.35 0 -0.35 -0.3 0.06 0.3 -0.3 0.06 0.3 0 0];
for i=1:11
k(i) = det([A(:,1:(i-1)) b' A(:,(i+1):11)])/det(A);
end
a1=k(1);b1=k(2);a2=k(3);b2=k(4);c2=k(5);a3=k(6);b3=k(7);c3=k(8);a4=k(9);b4=k(10);c4=k(11);
for i=1:2701
t(i) = (i-1)/300;
m = t(i);
x1(i) = (k(1)*m^5 - k(2)*10 * m^4 + k(3)*100 * m^3 - k(4)*1000 * m^2 + k(5)*10000 * m - k(6)*100000) * cos(m * 3);
end
x1 = x1 / max(x1) * (0.01 + 0.015 * rand);
3. Алгоритм управления по одной оси
3.1 Алгоритм управления по одной оси
3.1.1 Алгоритм стабилизации при наведении на определённую цель
Пусть есть установка, показанная на рисунке. На платформе установлен двигатель с осью вращения в точке О1. Сама платформа может колебаться – при этом по оси О она неподвижна, то есть колебания происходят относительно оси О.
На платформе установлен измеритель угловой скорости. Положение платформы будем определять углом отклонения от горизонтали в положительном или отрицательном направлении.
На оси, на которой установлен двигатель, имеется также датчик угла, определяющий угловое положение. Угол определяется отклонением луча О1 В от вертикали.
У нас заданы величины ОА – расстояние от точки О до цели, на которую будет наведение. И расстояние ОО1 - расстояние от точки О до оси вращения двигателя О1 .
Нам необходимо компенсировать колебания платформы вращением двигателя так, чтобы луч О1 В проходил через точку А. Это моделирует ситуацию с наведением на цель.

Рис 4.1.1 Схема установки
Будем считывать с интервалом ∆tпоказания с датчика угла и с измерителя угловой скорости, а также посылать сигнал на двигатель: угол поворота и угловая скорость.
Пусть вначале платформа находится в горизонтальном положении, а затем через время ∆tона повернулась на угол φ (рис. Н). Тогда чтобы луч О1 В проходил через точку А нужно повернуть двигатель на угол φ против часовой стрелки до вертикального положения. А затем на угол α также против часовой стрелки.
Найдём угол α с помощью заданных величин ОА = h, ОО1
= r. А также ![]() .
.
Из треугольника ОО1
С находим: ![]() ,
,
Отсюда ![]() .
.
![]()
Теперь можно найти tgα:  ;
;
Отсюда находим  .
.
Получили, что двигатель должен совершить поворот на угол (α+φ) против часовой стрелки.

Рис 4.1.2 Нахождение угла поворота ротора на первом шаге
Далее пусть прошло ещё ∆tвремени. Пусть двигатель был повёрнут на угол α1 = α от вертикали. А за время ∆tплатформа повернулась на угол φ1 и отклонение платформы равно углу φ – сумме двух поворотов.
В положении 2 необходимый угол отклонения от вертикали луча О1 В обозначим как α2. Угол α2 находится аналогично из величин h, r и угла φ:
 .
.
Чтобы перейти из положения 1 в положение 2 с наведением на цель, необходимы следующим образом поворачивать двигатель: сначала по часовой стрелке на угол α1, затем против часовой стрелки на угол (α2 + φ). То есть повернуть против часовой стрелки на угол (φ + (α2 – α1)) = (φ + Δ α), где Δ α = α2 – α1.

Рис 4.1.3 Нахождение угла поворота ротора на произвольном шаге
Мы знаем, как рассчитать угол поворота двигателя. Нам нужно, чтобы прогнозировался угол поворота платформы через Δt.
Так как Δtу нас мало – порядка десятков миллисекунд, то можно вначале считать угловую скорость ω1 с измерителя угловой скорости, установленного на платформе. А затем считать, что угол Δφ, на который повернётся платформа в течение Δtравным ω1Δt.
Также мы будем считывать и показания датчика угла – φ1 – угол определяющий положение платформы.
Тогда мы считаем, что через Δtположение платформы будет определяться углом φ = φ1 + Δφ. И поэтому можно найти углы α1 и α2 по формулам:
 ;
;
 .
.
И тогда нужно задать, что двигатель должен повернуться на угол α = α2 – – α1 + Δφс угловой скоростью ω = α / Δt.
Сформулируем алгоритм полностью:
1. Пусть начальное положение платформы горизонтальное и луч наведён на цель. Тогда φ = 0, α = 0, также заданы r и h;
Дальнейшие пункты повторяем при t = nΔt, где n = 0, 1, 2, …
2. Считываем угловую скорость платформы ω1;
3. Считываем положение платформы φ1;
4. Прогнозируем положение платформы через Δt: φ = φ1 + ω1Δt;
5. По формулам находим α1 и α2:
 ;
;  .
.
6. Подаем на двигатель значения угла, на который нужно совершить поворот и угловой скорости этого поворота: α = α2 – α1 + Δφ, ω = α / Δt.
3.1.2 Алгоритм стабилизации при сканировании
В данном случае установка остаётся такой же.
Теперь необходимо, чтобы луч О1 В в момент времени t проходил через точку cкоординатой x, где x = x(t) – изменяется со временем по определённому закону в некотором интервале (слева и справа от точки А). Пусть начало координат – точка А. Это моделирует ситуацию сканирования.
Пусть вначале платформа находится в горизонтальном положении, а затем через время ∆tона повернулась на угол φ (рис. Н). Тогда луч О1 В должен проходить через точку с координатой х = х(∆t) = ∆x. Для этого нужно повернуть двигатель на угол φ против часовой стрелки до вертикального положения. А затем на угол α также против часовой стрелки.
Найдём угол α с помощью заданных величин ОА = h, ОО1
= r. А также ![]() .
.
Из треугольника ОО1
С находим: ![]() ,
,
Отсюда ![]() .
.
![]()
Теперь можно найти tgα:  ;
;
Отсюда находим  .
.
Получили, что двигатель должен совершить поворот на угол (α+φ) против часовой стрелки

Рис 4.1.4 Нахождение угла поворота ротора на первом шаге.
Далее пусть прошло ещё ∆tвремени. Пусть двигатель был повёрнут на угол α1 = α от вертикали. А за время ∆tплатформа повернулась на угол φ1 и отклонение платформы равно углу φ – сумме двух поворотов.
В положении 2 луч проходит через точку х = x(2∆t) необходимый угол отклонения от вертикали луча О1 В обозначим как α2. Угол α2 находится аналогично из величин h, r и угла φ:
 .
.
Чтобы перейти из положения 1 в положение 2 при сканировании, необходимо следующим образом поворачивать двигатель: сначала по часовой стрелке на угол α1, затем против часовой стрелки на угол (α2 + φ). То есть повернуть против часовой стрелки на угол (φ + (α2 – α1)) = (φ + Δ α), где Δ α = α2 – α1.

Рис 4.1.5 Нахождение угла поворота ротора на произвольном шаге
Аналогично случаю с наведением на цель сформулируем алгоритм полностью:
1. Пусть начальное положение платформы горизонтальное и луч наведён на цель. Тогда φ = 0, α = 0, также заданы r и h;
Дальнейшие пункты повторяем при t = nΔt, где n = 0, 1, 2, …
2. Считываем угловую скорость платформы ω1;
3. Считываем положение платформы φ1;
4. Прогнозируем положение платформы через Δt: φ = φ1 + ω1Δt;
5. По формулам находим α1 и α2:
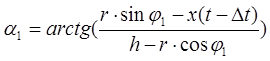 ;
;  .
.
6. Подаем на двигатель значения угла, на который нужно совершить поворот и угловой скорости этого поворота: α = α2 – α1 + Δφ, ω = α / Δt.
3.2 Реализация алгоритма
Реализуем алгоритм стабилизации при наведении на цель. Пусть Δt= 10 мсек, r= 1 м, h = 4 м. На рисунке 4.2.1 изображён график изменения углового положения платформы.

Рис 4.2.1 График изменения углового положения платформы
Происходят затухающие колебания платформы. При этом необходимо, чтобы движения ротора компенсировали данные колебания.
Необходимое угловое положение ротора при заданном угловом положении платформы определяется по формуле:
 . (4.2.1)
. (4.2.1)
При этом мы не можем считать по этой формуле, так как положение платформы в следующий момент времени мы определяем с ошибкой по положению и угловой скорости платформы в данный момент времени. На рисунке 4.2.2 изображён график движения ротора с ошибкой.

Рис 4.2.2 График изменения углового положения ротора
На каждом шаге мы определяем отклонение углового положения ротора от идеального, определяемого формулой (4.2.1).
График изменения данной ошибки показан на рисунке 4.2.3. Видно, что данная ошибка достаточно мала по сравнению со значениями углов.

Рис 4.2.3 График ошибки углового положения ротора
Теперь найдём значения отклонения положения луча от точки А, в которой он должен находится.
У нас есть формула, которая определяет значение угла поворота ротора, в зависимости от того в какую точку указывает луч:
 , где х – координата точки.
, где х – координата точки.
Из этой формулы мы можем найти значение х, подставляя в качестве φ значение углового положения платформы в данный момент, а в качестве α – значение реального угла поворота ротора в данный момент:

На рисунке 4.2.4 показан график изменения ошибки. Максимальная ошибка получилась меньше 1мм.

Рис 4.2.4 График отклонения положения луча от точки А
З аключение
В представленной дипломной работе была описана система сканирования и стабилизации изображения.
Рассмотрены системы координат, используемые при описании движения самолёта, такие как: географическая система координат, система координат центра масс самолёта и самолётная система координат. А также выведена формула перехода из координат центра масс к координатам самолётной системы.
Описаны принципы функционирования данной системы, алгоритм её работы. Проведено моделирование результатов работы системы по описанному алгоритму.
Были разработаны алгоритмы стабилизации по одной оси при сканировании по этой оси и наведении на цель, а также программная реализация этих алгоритмов.
Получены результаты работы данных алгоритмов.
П риложение
void CDiplom1Dlg::OnBnClickedStartButton()
{
int iInstallResult;
double ft;
iInstallResult=SetTimer(1, 10, NULL);
if(iInstallResult==FALSE)
{
MessageBox((LPCTSTR)L"Cannot install timer",
(LPCTSTR)L"Error message",
MB_OK+MB_ICONERROR);
}
m_XPrev = m_Graph.left + 5;
m_XPrev2 = m_Graph3.left + 5;
m_YPrev = m_Graph.bottom - 5 * 16 - 2 - 60;
m_YPrev3 = m_Graph3.bottom - 5 * 16 - 2;
m_YPrev4 = m_Graph4.bottom - 5 * 16 - 2;
ft = atan( sin(3.1415926/6)/(4 - cos(3.1415926/6)) );
m_ftPrev = 30;
m_YPrev2 = m_Graph2.bottom - 5 * 16 - 2 + 2 * (unsigned long)floor(ft*57.29578);
OnBnClickedClearButton();
DrawGrid(1);
DrawGrid(2);
DrawGrid(3);
DrawGrid(4);
m_Time = 0;
}
void CDiplom1Dlg::OnTimer(UINT_PTR nIDEvent)
{
double ft,t,t1,ft1,ft2,w,fi,dx;
m_Time += 0.01;
t = m_Time;
t1 = t;
ft = 30 * exp(-0.2*t) * cos(t*(2*3.1415926));
ft1 = - atan( sin(ft * 3.1415926/180)/(4 - cos(ft * 3.1415926/180)) );
w = (- 6 * exp(-0.2*(t-0.01)) * cos((t-0.01)*(2*3.1415926)) -
30 * (2*3.1415926) * exp(-0.2*(t-0.01)) * sin((t-0.01)*(2*3.1415926)) ) * 3.1415926/180;
fi = m_ftPrev * 3.1415926/180 + w / 100;
ft2 = - atan( sin(fi)/(4 - cos(fi)) );
dx = sin(ft * 3.1415926/180) - tan(-ft2) * (4 - cos(ft * 3.1415926/180));
if ((fmod(t,0.0625)<=0.005)||(fmod(t,0.0625)>0.0575))
{
m_XNext = m_XPrev + 1;
m_XNext2 = m_XPrev2 + 1;
m_YNext = m_Graph.bottom - 5 * 16 - 2 - 2*(unsigned long)floor(ft);
m_YNext2 = m_Graph2.bottom - 5 * 16 - 2 - (unsigned long)floor(2*ft2*57.29578);
m_YNext3 = m_Graph3.bottom - 5 * 16 - 2 - (unsigned long)floor(80*(ft1-ft2)*57.29578/0.025);
m_YNext4 = m_Graph4.bottom - 5 * 16 - 2 - (unsigned long)floor(80*1000*dx);
DrawLine();
m_XPrev = m_XNext;
m_XPrev2 = m_XNext2;
m_YPrev = m_YNext;
m_YPrev2 = m_YNext2;
m_YPrev3 = m_YNext3;
m_YPrev4 = m_YNext4;
}
m_ftPrev = ft;
if (m_XNext == m_Graph.left + 245)
OnBnClickedStopButton();
CDialog::OnTimer(nIDEvent);
}
void CDiplom1Dlg::DrawGrid(int numG)
{
unsigned long y_b;
unsigned long y_t;
unsigned long x_l;
unsigned long x_r;
unsigned long x[16],y[11],f[11],s1,s2;
double dx,dy;
int i;
if (numG == 1)
{
y_b = m_Graph.bottom - 2;
y_t = m_Graph.top - 2;
x_l = m_Graph.left + 5;
x_r = m_Graph.right;
}
if (numG == 2)
{
y_b = m_Graph2.bottom - 2;
y_t = m_Graph2.top - 2;
x_l = m_Graph2.left + 5;
x_r = m_Graph2.right;
}
if (numG == 3)
{
y_b = m_Graph3.bottom - 2;
y_t = m_Graph3.top - 2;
x_l = m_Graph3.left + 5;
x_r = m_Graph3.right;
}
if (numG == 4)
{
y_b = m_Graph4.bottom - 2;
y_t = m_Graph4.top - 2;
x_l = m_Graph4.left + 5;
x_r = m_Graph4.right;
}
CClientDC dc(this);
dx = (x_r - x_l) / 15;
dy = (y_b - y_t) / 10;
s1 = floor(dx);
s2 = floor(dy);
COLORREF m_PenColor = RGB(0,0,255);
CPen m_Pen;
m_Pen.CreatePen(2/*PS_SOLID*/, 1, m_PenColor);
dc.SelectObject(&m_Pen);
for (i=0;i<11;i++)
{
x[i] = x_l + i * s1;
y[i] = y_b - i * s2;
}
for (i=11;i<16;i++)
x[i] = x_l + i * s1;
for (i=0;i<11;i++)
{
dc.MoveTo(x[i],y[0]);
dc.LineTo(x[i],y[10]);
dc.MoveTo(x[0],y[i]);
dc.LineTo(x[15],y[i]);
}
for (i=11;i<16;i++)
{
dc.MoveTo(x[i],y[0]);
dc.LineTo(x[i],y[10]);
}
m_Pen.DeleteObject();
m_Pen.CreatePen(PS_SOLID, 1, m_PenColor);
dc.SelectObject(&m_Pen);
dc.MoveTo(x[0],y[0]);
dc.LineTo(x[0],y[10]);
dc.MoveTo(x[0],y[5]);
dc.LineTo(x[15],y[5]);
m_Pen.DeleteObject();
m_ResultsEdit.Format(L"bottom = %d, top = %d, left = %d, right = %d, dx = %d, dy = %d",y_b,y_t,x_l,x_r,s1,s2);
UpdateData(FALSE);
}
void CDiplom1Dlg::DrawLine(void)
{
CClientDC dc(this);
COLORREF m_PenColor = RGB(255,0,0);
CPen m_Pen;
m_Pen.CreatePen(0, 1, m_PenColor);
dc.SelectObject(&m_Pen);
dc.MoveTo(m_XPrev,m_YPrev);
dc.LineTo(m_XNext,m_YNext);
dc.MoveTo(m_XPrev,m_YPrev2);
dc.LineTo(m_XNext,m_YNext2);
dc.MoveTo(m_XPrev2,m_YPrev3);
dc.LineTo(m_XNext2,m_YNext3);
dc.MoveTo(m_XPrev2,m_YPrev4);
dc.LineTo(m_XNext2,m_YNext4);
m_Pen.DeleteObject();
}
с писокиспользованнойлитературы
1. Самарский А. А., Михайлов А. П. «Математическое моделирова-
ние: Идеи. Методы. Примеры» Физматлит, 2001 г, 320 с;
2. http://aqua.sm.bmstu.ru/study/student/Library/CoodrSys.htm;
3. Проектирование следящих систем. Колл. авторов. Под ред. Л.В. Рабиновича.М.: Машиностроение, 1969.-500 с.
4. Следящие приводы. В 2-х кн. Под ред. Б.К. Чемоданова.-М.: Энергия, 1976.-384 с., ил.
5. http://ru.wikipedia.org;
6. http://www.optolink.ru;
7. http://www.modem-techno.ru;
8. http://www.skbis.ru.

