| Скачать .docx |
Курсовая работа: Курсовая работа: Проектирование зеркальных антенн и устройств СВЧ
Министерство образования Российской Федерации
Таганрогский Технологический Институт
Южного Федерального Университета
Кафедра АиРПУ
Курсовой проект
на тему: «Проектирование зеркальных антенн и устройств СВЧ».
Таганрог 2007
Техническое задание
Рассчитать антенну, предназначенную для радиолокационного спидометра.
Технические условия
1. Ширина основного лепестка диаграммы направленности по уровню 0,5 в рабочем диапазоне:
а) в плоскости Н 2,8 град
б) в плоскости Е 3,4 град
2. Рабочий диапазон 10300±5% МГц
3. Уровень 1-го бокового лепестка (по отношению к основному по мощности):
а) в плоскости Н -26,6 дБ
б) в плоскости Е -22,8 дБ
4. Поляризация поля вертикальная
5. Длина фидера 3,1 м
6. КСВ в тракте, не более 1,07
7 Мощность передатчика в импульсе .500Е - 03 кВт
8. Устройство СВЧ: балансный смеситель
Содержание
Введение
1. Выбор формы раскрыва зеркала
2. Выбор функции амплитудного распределения поля в раскрыве зеркала
3. Расчет размеров раскрыва
4. Расчет ДН облучателя
5. Выбор и проектирование облучателя
6. Проектирование рупорного облучателя
7. Расчет реального распределения поля и ДН зеркала
Введение
Зеркальные антенны являются наиболее распространенными типом направленных антенн в сантиметровом, дециметровом и отчасти метровом диапазонах волн. Широкое использование зеркальных антенн объясняется простотой конструкции, возможностью получения почти любого применяемого на практике типа ДН, высоким КПД, малой шумовой температурой, хорошими диапазонными свойствами и т.д.
В зеркальных антеннах применяются следующие основные типы зеркал: параболические (параболоид вращения, усеченный параболоид, параболический цилиндр), сферические, плоские и уголковые, специальной формы, двух- и многозеркальные.
В радиолокационных применениях зеркальные антенны позволяют легко получить равносигнальную зону, допускают одновременное формирование нескольких ДН общим зеркалом (в том числе суммарных и разностных). Некоторые типы зеркальных антенн могут обеспечивать достаточно быстрое качание луча в значительном угловом секторе. Зеркальные антенны являются наиболее распространенным типом антенн в космической связи и радиоастрономии, и именно с помощью зеркальных антенн удается создавать гигантские антенные сооружения с эффективной поверхностью раскрыва, измеряемой тысячами квадратных метров.
1. Выбор формы раскрыва зеркала
Последовательность расчета излучающей части зеркальной антенны (ЗА) зависит от характера технического задания (ТЗ) на проектирование.
Как правило в ТЗ заданы целевое назначение антенны, рабочая частота и требования к направленным свойствам ЗА, которые необходимо проанализировать.
Классическими представителями зеркальных антенн являются параболические антенны, которые могут выполняться в виде параболоида вращения, параболического цилиндра или закрытой конструкции, ограниченной параллельными проводящими плоскостями.
Для выбора формы раскрыва антенны необходимо проанализировать отношение ширины ДН в плоскости Е и Н. Для моего варианта это отношение
3.4/2.8 = 1.21 < 2
Следовательно, форму раскрыва зеркала выбираем круглую. Это может быть параболоид вращения, он возбуждается слабонаправленным облучателем (например, рупором), помещенным в фокусе зеркала, и преобразует сферический фронт волны в плоский.
Принцип работы параболической антенны состоит в следующем: она состоит из металлического отражателя (рефлектора) 1, облучателя 2, помещаемого в фокусе параболоида вращения, и питающего фидера 3 (рис. 1.).

Рис. 1.
Облучатель антенны выполняется так, чтобы почти вся излучаемая им энергия направлялась в сторону отражателя. Электромагнитные волны возбуждают на его поверхности высокочастотные токи, которые создают свои электромагнитные поля. Так как отражающей поверхности придается параболическая форма, сумма расстояний от фокуса до поверхности отражателя и от отражателя до плоскости, перпендикулярной фокальной оси, является постоянной величиной, поэтому к поверхности раскрыва антенны переизлученные колебания приходят в одной и той же фазе.
В результате сложения отраженных колебаний в раскрыве антенны образуется и затем распространяется вдоль ее оси плоская волна.
Укажем основные геометрические параметры параболических зеркал:
R, f - радиус и фокусное расстояние зеркала; y0 - угол раскрыва зеркала;
p(Y) - профиль зеркала; x-координата точки в раскрыве зеркала. Эти параметры связаны между собой простыми соотношениями:

2. Выбор функции амплитудного распределения поля в раскрыве зеркала
Выберем функцию амплитудного распределения в соответствии с заданным условием из таблиц.
![]()
![]() , где p=2 Δ=0.7
, где p=2 Δ=0.7
![]()
![]() , где p=2 Δ=0.6
, где p=2 Δ=0.6
Графики соответствующих распределений:

Рис. 2 Распределение поля в Н - плоскости раскрыва.

Рис. 3 Распределение поля в E - плоскости раскрыва.
3. Расчет размеров раскрыва
Размеры раскрыва зависят от ширины ДН, рабочей длины волны и выбранных функций распределения.
Коэффициенты ![]() в двух плоскостях:
в двух плоскостях: ![]()
![]()
Ширина ДН в двух плоскостях из ТЗ: ![]()
![]()
Найдем длину волны: ![]()
Найдем размеры: ![]()
![]()
Выберем радиус по большему размеру: R = b/2, R = 35 см.
Для обеспечения заданной ширины диаграммы направленности в качестве раскрыва возьмем симметрично-усеченный параболоид вращения.
4. Расчет ДН облучателя
В параболоиде вращения (или усеченном параболоиде вращения) облучатель должен создавать сферическую волну. У такой волны амплитуда убывает с увеличением расстояния r от источника (облучателя) обратно пропорционально r (в среде без потерь). После отражения от зеркала фронт волны становится плоским, а амплитуда плоской волны в среде без потерь не зависит от расстояния.
Исходя из сказанного выше, связь ДН облучателя f(y) и поля в раскрыве с точностью до постоянного множителя можно записать в виде:
![]() ,
,
где ![]() .
.
Нормируя ДН по максимуму fмакс (y) = r(0) Е(0) = f, получим расчетную формулу для нормированной ДН облучателя:
![]() .
.
Из рис. 1 видно, что
![]() ,
,
![]() .
.
Видно, что нормированную координату x нужно находить по следующей формуле:
![]() .
.
Значение y0
выбирают ориентировочно в пределах 58° – 62°. Это дает возможность обеспечить в дальнейшем достаточно высокий КИП при сравнительно небольших размерах облучателя, и, как следствие, с меньшим затенением зеркала. С уменьшением y0
необходимая ДН облучателя может получится настолько широкой, что размеры облучателя станут меньше, чем, например, даже у открытого конца волновода. Зададимся углом раскрыва в плоскости Е: ![]() .
.
Знание угла ![]() и размера раскрыва позволяет найти фокусное расстояние зеркала по формуле:
и размера раскрыва позволяет найти фокусное расстояние зеркала по формуле:
![]() , f = 30.174 см.
, f = 30.174 см.
Так как фокусное расстояние параболоида вращения (или усеченного параболоида) в другой плоскости должно быть таким же, то угол раскрыва в другой плоскости ![]() определяется автоматически через fи размер b в этой плоскости. Поскольку
определяется автоматически через fи размер b в этой плоскости. Поскольку ![]() , то
, то ![]() ,
, ![]() .
.
Далее, рассчитываем ДН облучателя в плоскостях Е и Н соответственно:
![]() ,
,
где ![]()
![]() ,
,
где ![]()

Рис. 4. ДН облучателя в плоскости Е

Рис. 5. ДН облучателя в плоскости Н
Из рис. 4 и рис. 5 легко определить ширину ДН облучателя в главных плоскостях: ![]() и
и ![]() .
.
5. Выбор и проектирование облучателя
К облучателю обычно предъявляет следующие требования:
а) он должен реализовывать рассчитанную ранее диаграмму направленности в секторе углов ![]() и иметь минимальное излучение вне этого сектора;
и иметь минимальное излучение вне этого сектора;
б) его поперечные размеры должны быть минимальными для снижения затенения раскрыва;
в) облучатель должен иметь устойчивый общий фазовый центр в двух плоскостях, совмещаемый с фокусом параболоида вращения;
г) электрическая прочность облучателя должна быть достаточной для пропускания полной рабочей мощности передатчика в импульсе без опасности пробоя;
д) рабочая полоса частот облучателя должна соответствовать требуемой полосе частот антенны;
е) конструкция облучателя должна обеспечивать необходимую стойкость к метеоусловиям и допускать возможность герметизации всего фидерного тракта;
В качестве облучателя возьмем пирамидальный рупор (рис. 6).
6. Проектирование рупорного облучателя

Рис. 6. Пирамидальный рупор.
Расчет рупорной антенны сводится к расчету ее геометрических размеров. Размеры раскрыва ![]() и
и ![]() выбираем на основе найденных ранее ДН облучателя в двух плоскостях.
выбираем на основе найденных ранее ДН облучателя в двух плоскостях.
![]()
![]()
Скорректированные размеры размеров рупора: ![]()
Найдём размеры ![]() волновода исходя из следующих соображений: волновод должен обеспечить прохождение лишь волны основного типа, пропускать необходимую мощность. Для этих целей подходит стандартный волновод 23x10 мм. Из табл. 3. [1] находим – данный волновод допускает
волновода исходя из следующих соображений: волновод должен обеспечить прохождение лишь волны основного типа, пропускать необходимую мощность. Для этих целей подходит стандартный волновод 23x10 мм. Из табл. 3. [1] находим – данный волновод допускает ![]() кВт, что больше необходимой мощности. Из той же таблицы выбираем материал с наименьшими потерями – медь (
кВт, что больше необходимой мощности. Из той же таблицы выбираем материал с наименьшими потерями – медь (![]() дБ/м).
дБ/м).
Определим длину оптимального рупора ![]() в Н-плоскости:
в Н-плоскости:

численно ![]() см. Зная
см. Зная ![]() , определяем длину рупора в Е-плоскости из условия стыковки рупора с волноводом:
, определяем длину рупора в Е-плоскости из условия стыковки рупора с волноводом:
![]()
![]() см. Для того, чтобы рупор был оптимальным необходимо выполнение условия
см. Для того, чтобы рупор был оптимальным необходимо выполнение условия
![]()
![]() см, т.е. условие оптимальности в Е-плоскости тоже выполняется,
см, т.е. условие оптимальности в Е-плоскости тоже выполняется,
Рассчитаем фазовые ошибки:
 ,
, ![]()
Рассчитаем реальную диаграмму направленности рупора.
В Е-плоскости
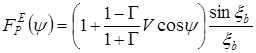
где  - параметр;
- параметр; ![]() - модуль коэффициента отражения волны от раскрыва рупора;
- модуль коэффициента отражения волны от раскрыва рупора; ![]() ;
; ![]() .
.
В Н-плоскости
![]()
где ![]() .
.
![]()

Рис. 7. Реальная и требуемая ДН облучателя в плоскости Е
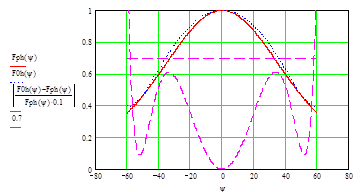
Рис. 8. Реальная и требуемая ДН облучателя в плоскости Н
Рассчитаем положения фазовых центров рупора в главных плоскостях:
![]() ,
,
![]()
![]()
Допуск на смещение фазового центра облучателя из фокуса вдоль оси:
![]()
Расстояние ![]() между фазовыми центрами удовлетворяет допуску на смещение фазового центра облучателя из фокуса зеркала вдоль его оси.
между фазовыми центрами удовлетворяет допуску на смещение фазового центра облучателя из фокуса зеркала вдоль его оси.
7. Расчет реального распределения поля и ДН зеркала
Расчет проводится для сравнения реального ![]() и требуемого
и требуемого ![]() распределений в раскрыве зеркала. В усеченном параболоиде вращения реальная ДН связана с нормированной ДН облучателя следующим соотношением:
распределений в раскрыве зеркала. В усеченном параболоиде вращения реальная ДН связана с нормированной ДН облучателя следующим соотношением:
![]() ,
,
где ![]() .
.
Графики реального и идеального распределения и их относительной ошибки строятся на одном графике. Ошибка не должна превышать 7 %.
Учитывая все вышесказанное, проведем расчет реального распределения поля в зеркале:
1) Расчет реального амплитудного распределения поля в Е плоскости
Функция реального распределения имеет вид:
![]() ,
,
где ![]() .
.

Рис.9 График реального распределения поля в E плоскости
2) Расчет реального амплитудного распределения поля в Н плоскости
Функция реального распределения имеет вид:
![]() ,
,
где ![]() .
.

Рис. 10. Реальное и идеальное распределение поля в Н плоскости и их относительная ошибка.
Расчёт ДН ведётся исходя из формул, приведенных в [1]. Эти формулы приведены без учёта ДН элемента Гюйгенса, поэтому домножим их на ![]() :
:

где ![]() ;
;  .
.
Диаграмму направленности будем строить в логарифмическом масштабе. Для этого преобразуем к виду
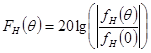 .
.
Аналогично для Е-плоскости:

где ![]() ;
;  ;
;
или в логарифмическом масштабе
 .
.

Рис. 11. ДН зеркальной антенны в Е-плоскости

Рис. 12. ДН зеркальной антенны в H-плоскости