Реферат: Комбинированый метод для вычисления корня уравнения

2.1 Цель работы:

Изучить комбинированный метод для вычисления действительного корня уравнения, уметь использовать данный метод для решения уравнений с использованием ЭВМ.

2.2 Расчётные формулы

Расчётная формула вычисления -го приближения по методу касательных:

.

Расчётная формула вычисления -го приближения по методу хорд:

.

Начальное приближение для метода касательных выбирают в соответствии с условием:

, если ,

или , если .

Начальное приближение для метода хорд тогда принимается , или соответственно.

Процесс вычисления корня останавливается, когда выполняется условие:

,

где – заданная точность.

За приближенное значение корня уравнения принимается:

.

2.3 Подготовительная работа

Вычислить корень уравнения с точность комбинированным методом.

Графически отделим корни. Для этого данное уравнение запишем в виде . Строим графики функций и (рис. 2.1).

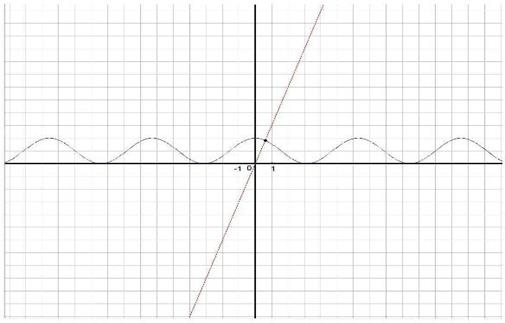
Рисунок 2.1

Точный корень уравнения , отрезок [0;1] – интервал изоляции корня.

Проверяем условия, гарантирующие единственность корня на [0;1] и сходимость метода:

непрерывна на [0;1] и не меняет знак:.

непрерывна на [0;1] и не меняет знак:.

За начальное приближение для метода касательных берём , для метода хорд .

Процесс вычисления корня:

.

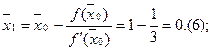
Условие не выполняется, процесс вычисления корня продолжается до достижения заданной точности .

Требуемая точность вычисления результата была достигнута за 2 итерации. Результат 0,607199.

2.4 Текст программной реализации

#include <iostream>

#include <math.h>

using namespace std;

double f(double x)

{

return 3*x-cos(x)-1;

}

double fw(double x)

{

return 3+sin(x);

}

void main()

{

double xk, xh, tochnost, otvet;

cout<<"Vvedite nachalnoe priblizhenie po metodu kasatelnih xk=";

cin>>xk;

cout<<"\nVvedite nachalnoe priblizhenie po metodu hord xh=";

cin>>xh;

cout<<"\nX-hord\t\tX-kasatelnih\tTochnost\n-----------------------------------";

int n;

for(n=0; n<20; n++)

{

xh -= f(xh)*(xk-xh)/(f(xk)-f(xh));

xk -= f(xk)/fw(xk);

tochnost=fabs(xh-xk);

cout<<'\n'<<xh<<'\t'<<xk<<'\t'<<tochnost;

if(tochnost<0.001) break;

};

n++;

otvet=(xh+xk)/2;

cout<<"\n\nKolichestvo iteraciy="<<n;

cout<<'\n'<<'\n'<<"Koren uravneniya="<<otvet;

cin>>xk;

}