| Скачать .docx |
Реферат: Основні поняття та визначення ЕЕГ Ряд та інтеграл Фурє
Основні поняття та визначення ЕЕГ. Ряд ТА інтеграл Фур'є
1. Ритми ЕЕГ дорослої людини, яка не спить
Електроенцефалографія (ЕЕГ) є одним з методів одержання біомедичної інформації.
Електроенцефалографія – це метод дослідження головного мозку, який полягає у реєстрації його електричних потенціалів. ЕЕГ являє собою складний коливальний електричний процес, що може бути зареєстрований при розташуванні електродів на мозку чи на поверхні скальпа. ЕЕГ є результатом електричної підсумовування і фільтрації елементарних процесів, що протікають у нейронах головного мозку.
Спектр ЕЕГ є досить складним: існує класифікація ритмів ЕЕГ по деяких основних діапазонах. Під поняттям «ритм» на ЕЕГ розуміється визначена смуга частот. До ритмів ЕЕГ дорослої людини, яка не спить, відносяться альфа ![]() , бета
, бета ![]() , мю
, мю![]() -ритми.
-ритми.
Альфа-ритм характеризується частотою 8÷13 Гц, амплітудою до 100 мкВ. Реєструється у 85÷95% здорових дорослих обстежуваних; найкраще виражений у потиличних відділах, за напрямком наперед амплітуда його поступово зменшується. Для здорових людей характерний відносно вузький діапазон ![]() -ритму. Найбільшу амплітуду
-ритму. Найбільшу амплітуду ![]() -ритм має у стані спокійного розслабленого очікування. Його амплітуда істотно змінюється в часі. Досить регулярно спостерігаються спонтанні зміни амплітуди, так звані «веретена», що виражаються в наростанні і зниженні амплітуди почергово. При підвищенні рівня функціональної активності мозку амплітуда
-ритм має у стані спокійного розслабленого очікування. Його амплітуда істотно змінюється в часі. Досить регулярно спостерігаються спонтанні зміни амплітуди, так звані «веретена», що виражаються в наростанні і зниженні амплітуди почергово. При підвищенні рівня функціональної активності мозку амплітуда ![]() -ритму зменшується, і часто він цілком зникає.
-ритму зменшується, і часто він цілком зникає.
Бета-ритм характеризується частотою 14÷40 Гц, амплітудою до 15 мкВ. Найкраще ![]() -ритм реєструється в області передніх центральних звивин, однак поширюється і на задні центральні і лобові звивини. У нормі він дуже слабко виражений і зазвичай має амплітуду 3÷7 мкВ. При русі чи навіть при розумовому представленні його
-ритм реєструється в області передніх центральних звивин, однак поширюється і на задні центральні і лобові звивини. У нормі він дуже слабко виражений і зазвичай має амплітуду 3÷7 мкВ. При русі чи навіть при розумовому представленні його ![]() -ритм зникає в зоні відповідної коркової проекції.
-ритм зникає в зоні відповідної коркової проекції.
Мю-ритм характеризується частотою 8÷13 Гц, амплітудою до 50 мкВ. ![]() -ритм, названий також аркоподібним ритмом, спостерігається в тім'яно-центральній області і має параметри, що збігаються з параметрами нормального
-ритм, названий також аркоподібним ритмом, спостерігається в тім'яно-центральній області і має параметри, що збігаються з параметрами нормального ![]() -ритму. Спостерігається в 5÷15% дорослих обстежуваних. Активізується
-ритму. Спостерігається в 5÷15% дорослих обстежуваних. Активізується ![]() -ритм під час розумового навантаження і психічної напруги.
-ритм під час розумового навантаження і психічної напруги.
2. Види активності, патологічні для дорослої людини, яка не спить
До патологічних проявів на ЕЕГ відноситься поява повільних ритмів: тета ![]() і дельта
і дельта![]() . Чим нижче їхня частота і вище амплітуда, тим більше виражений патологічний процес. Тета -ритм характеризується частотою 4÷6 Гц, амплітуда перевершує 40 мкВ, досягаючи при деяких патологічних станах 300 мкВ і більше. Дельта-ритм характеризується частотою 0,5÷3 Гц, амплітуда така сама, як у
. Чим нижче їхня частота і вище амплітуда, тим більше виражений патологічний процес. Тета -ритм характеризується частотою 4÷6 Гц, амплітуда перевершує 40 мкВ, досягаючи при деяких патологічних станах 300 мкВ і більше. Дельта-ритм характеризується частотою 0,5÷3 Гц, амплітуда така сама, як у ![]() -ритму. На ЕЕГ дорослої людини, яка не спить, можуть зустрічатися
-ритму. На ЕЕГ дорослої людини, яка не спить, можуть зустрічатися ![]() і
і ![]() -ритми в невеликій кількості і з амплітудою, що не перевищує амплітуду
-ритми в невеликій кількості і з амплітудою, що не перевищує амплітуду ![]() -ритму. У цьому випадку говорять про визначене зниження рівня функціональної активності мозку.
-ритму. У цьому випадку говорять про визначене зниження рівня функціональної активності мозку.
Одним з важливих аспектів застосування ЕЕГ є вивчення епілепсії. Дані сучасних досліджень свідчать про те, що мозок при епілепсії характеризується рядом функціональних перебудов на макро- і мікроструктурному рівні. Показано наявність деполяризаційного зсуву потенціалу мембрани нейронів, що визначає їхню підвищену схильність до генерації потенціалів дії. Це призводить у свою чергу до підвищення обсягу процесів збудження, розгальмовування шляхів і зв'язків, що у нормі загальмовані. У результаті в синхронні розряди втягуються набагато більші обсяги мозкових структур, ніж у нормі. Отже, однією з основних особливостей мозку при епілепсії є властивість нейронів давати більш активні реакції збудження і вступати у синхронізовану активність. Процес синхронізації активності нейронів приводить до наростання амплітуди ЕЕГ у результаті підсумовування амплітуд синфазних коливань.
У випадку, якщо розряди окремих нейронів синхронні в часі, крім наростання амплітуди, має спостерігатися також і зменшення тривалості сумарного потенціалу, що приводить до утворення короткого і високоамплітудного піка (спайка). Цей потенціал має пікоподібну форму, його тривалість 5-50 мс (рис. 1а). Амплітуда спайка зазвичай перевершує амплітуду фонової активності і може досягати сотень – тисяч мкВ. Піки можуть мати й менші амплітуди. Найчастіше піки групуються в пачки, що носять назву «множинні піки». Важливою ЕЕГ-ознакою епілепсії є також наявність так званих гострих хвиль, епізодичних чи стійких (рис. 1б). Зовні гостра хвиля нагадує пік і відрізняється від нього тільки розтягнутістю в часі. Тривалість гострої хвилі більше 50 мкс. Амплітуда така сама, як у спайків. Часто піки супроводжуються повільними хвилями, утворюють комплекс пік – хвиля (рис. 1г). Їхня поява буває генералізованою, або вони реєструються у вигляді локальних розрядів, що свідчить про епілептичне вогнище. Оскільки ![]() -хвилі мають невелику тривалість, то при збільшенні їхньої амплітуди до 40÷50 мкВ вони приймають загострену форму, що характерно для деяких форм епілепсії. Ці коливання зазвичай не називають
-хвилі мають невелику тривалість, то при збільшенні їхньої амплітуди до 40÷50 мкВ вони приймають загострену форму, що характерно для деяких форм епілепсії. Ці коливання зазвичай не називають ![]() -ритмом, а позначають як гострі хвилі (рис. 1в). Аналогічне наростання амплітуди
-ритмом, а позначають як гострі хвилі (рис. 1в). Аналогічне наростання амплітуди ![]() -ритму вище 150÷200 мкВ трактується не як звичайний
-ритму вище 150÷200 мкВ трактується не як звичайний ![]() -ритм, а як гострі
-ритм, а як гострі ![]() -подібні хвилі, особливо коли вони йдуть у вигляді спалахів на більш низькому амплітудному фоні.
-подібні хвилі, особливо коли вони йдуть у вигляді спалахів на більш низькому амплітудному фоні.
Гострі хвилі і піки найчастіше комбінуються з повільними хвилями. Комплекс, що виникає при комбінації піка з хвилею, називається «піки – хвилі» (рис. 1д). Зазвичай ці комплекси мають високу амплітуду, причому амплітуди піка і хвилі, як правило, корелюють. Комплекси піки – хвилі зазвичай йдуть серіями повторюваних феноменів, причому при накладанні вони збігаються. Часто кілька піків комбінуються з однією хвилею. Такий комплекс називається «множинні піки – хвилі».
Комплекс, що нагадує за формою комплекс піки – хвилі, але має велику амплітуду, називається «гостра хвиля – повільна хвиля» (рис. 1е). Зазвичай повільна хвиля має більшу тривалість, ніж хвиля, що йде за піком у комплексі піки – хвилі. Частота комплексів піки – хвилі складає 2,5-6 Гц. Частота комплексів гостра хвиля – повільна хвиля – 0,7-2 Гц.
Наявність епілептичних феноменів у мозку є прямим доказом того, що у відповідній області відбуваються гіперсинхронні, патологічні розряди великих груп нервових клітин. Повторне виявлення епілептичних розрядів у визначеній постійній області мозку свідчитиме про наявність фокального епілептичного ураження.
Одним з основних критеріїв при аналізі ЕЕГ є симетрія. Під симетричністю ЕЕГ розуміють істотний збіг частот, амплітуд і фаз симетричних областей двох півкуль мозку. Відносно патологічних форм активності говорять про сторону її амплітудної переваги, а не абстрактно про її асиметрію. За поширеністю цих асиметричних патологічних коливань говорять про порушення півкулі, коли зміни охоплюють усю півкулю, і фокальних (зазвичай максимально виражаються під одним електродом і різко знижуються за представленням й амплітудою під сусідніми).
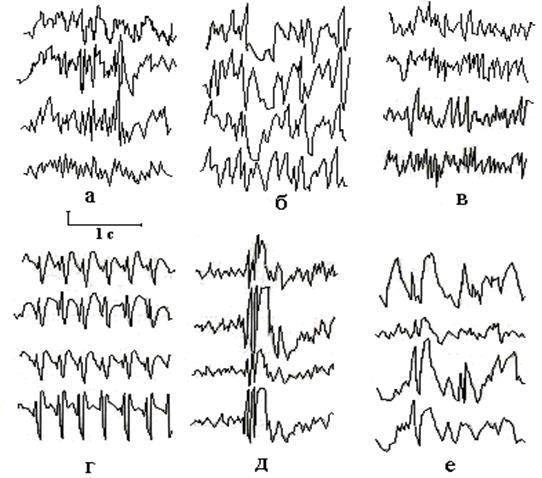
Рисунок 1 – Основні типи епілептичної активності
3. Артефакти на ЕЕГ та їхнє усунення
Артефакти на ЕЕГ поділяються на дві групи – фізичні і фізіологічні.
Фізичні артефакти обумовлені порушеннями технічних правил реєстрації ЕЕГ. Зазвичай це перешкоди від електричних полів, які створюються пристроями промислового електричного струму. Вони легко розпізнаються, оскільки являють собою синусоїдальні коливання частотою 50 Гц (рис. 2). У деяких електроенцефалографах передбачені вузькосмугові фільтри, які усувають вузьку смугу в області 50 Гц (рис. 3а).
Інший тип артефактів представлений різкими стрибками позитивних і негативних відхилень напруги (рис. 3б). Від пароксизмальних розрядів ці артефакти відрізняються формою, крутизною, раптовістю появи.
Причини цих перешкод:
· мінливість контакту і рух електродів;
· поляризація електрода;
· нагромадження електричних зарядів на тілі обстежуваного.
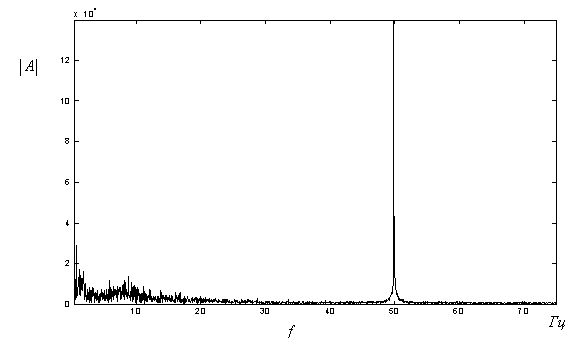
Рисунок 2 – Спектр ЕЕГ з завадою мережі
Іноді мають місце артефакти від електромагнітних завад, створених спалахами світла фотостимулятора (рис. 3в). Їхня амплітуда не залежить від частоти мигтіння і набагато перевершує амплітуду власних коливань ЕЕГ.
Фізіологічні артефакти пов'язані з проявами життєдіяльності організму і мають такі причини:
· потенціали, обумовлені діяльністю м'язів, – електроміограма (ЕМГ) (рис. 3г);
· електричні потенціали, пов'язані з рухом очей, – електроокулограма (ЕОГ) (рис. 3з);
· потенціали електрокардіограми (ЕКГ) (рис. 3д);
· електричні потенціали, викликані ковтальними рухами (рис. 3е);
· електричні потенціали, пов'язані зі змінами фізіологічного стану шкіри (рис. 3ж).
ЕМГ являє собою нерегулярну високочастотну (15–100 Гц) електричну активність загостреної форми. Амплітуда ЕМГ може приймати різні значення. ЕМГ може бути найбільш виражена в потиличних, скроневих і лобових відведеннях. Від нормального ![]() -ритму артефакти ЕМГ відрізняються більшою амплітудою, більш нерегулярним і високочастотним ритмом. Комп'ютерні методи аналізу дозволяють розрізняти
-ритму артефакти ЕМГ відрізняються більшою амплітудою, більш нерегулярним і високочастотним ритмом. Комп'ютерні методи аналізу дозволяють розрізняти ![]() -ритм та ЕМГ. Спектральна щільність потужності
-ритм та ЕМГ. Спектральна щільність потужності ![]() -ритму має пік в області 15–20 Гц, а спектральна щільність потужності ЕМГ зазвичай має пік в області 70 Гц, що може служити відмінністю при комп'ютерному аналізі.
-ритму має пік в області 15–20 Гц, а спектральна щільність потужності ЕМГ зазвичай має пік в області 70 Гц, що може служити відмінністю при комп'ютерному аналізі.
Потенціали ЕКГ легко розпізнаються за характерною формою і появою через рівні проміжки часу, що відповідають періоду скорочень серця. Вони обумовлені неоднаковою відстанню електродів від серця, за рахунок чого виникає різниця потенціалів ЕКГ. Спостерігаються відносно рідко.
Потенціали ЕОГ найчастіше мають форму одно– чи двофазних коливань з періодом 0,3–1 с. Іноді частота ЕОГ вище – 4–6 Гц. Звідси випливає, що частотний діапазон ЕОГ збігається з ![]() і
і ![]() хвилями, що може привести до помилкової діагностики. Відмінними ознаками ЕОГ є їхній просторовий розподіл. Максимальна їхня амплітуда реєструється в лобових відведеннях і за напрямком назад швидко зменшується. Форма цих артефактів дуже характерна і стереотипна. Крім того, розпізнати їх можна, використовуючи реєстрацію ЕОГ за допомогою додаткових електродів, розташованих біля очей.
хвилями, що може привести до помилкової діагностики. Відмінними ознаками ЕОГ є їхній просторовий розподіл. Максимальна їхня амплітуда реєструється в лобових відведеннях і за напрямком назад швидко зменшується. Форма цих артефактів дуже характерна і стереотипна. Крім того, розпізнати їх можна, використовуючи реєстрацію ЕОГ за допомогою додаткових електродів, розташованих біля очей.
Електричні потенціали, викликані ковтальними рухами, являють собою повільні хвилі з періодом 0,5–2 с, що зазвичай поширюються при монополярному відведенні по всіх каналах.
Електричні потенціали, викликані зміною стану шкірних покривів, являють собою повільні хвилі високої амплітуди з періодом 1–5 с, що зазвичай поширюються по всіх каналах. Усунення цих артефактів пов'язане з істотними труднощами. Допомагає повторне зняття ЕЕГ.
Іноді мають місце артефакти, пов'язані з рухом електрода і зміною потенціалу шкіри в результаті механічних зсувів унаслідок пульсації розташованої поблизу артерії. Вони мають форму і частоту пульсограми. Ці артефакти легко усуваються зміною місця розташування електрода. Основне правило, яким керується досвідчений лікар при аналізі ЕЕГ: «Будь-яка активність у ЕЕГ, яка реєструється тільки під одним електродом, є артефактом». Основні види артефактів наведені на рис. 3.
Правильне інтерпретування сигналів на ЕЕГ – це якоюсь мірою мистецтво. Зміни, схожі з епілептичними розрядами, можуть викликатися рухом очей і м'язами голови, пульсацією кровоносних судин, дихальними рухами, роботою серця, жуванням, ковтанням, доторканням до електрода, пересуванням інших людей по кімнаті, де проводиться дослідження.
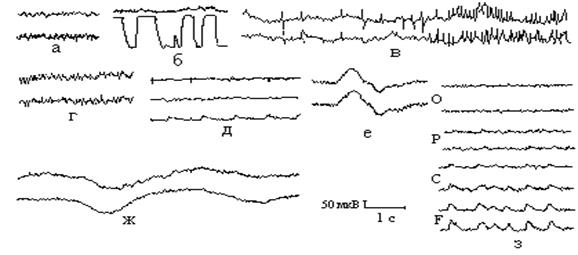

Рисунок 3 – Основні види артефактів
4. Визначення спектральної щільності ЕЕГ
4.1 Ряд та інтеграл Фур'є
Поняття про розкладання Фур'є можна вважати вам уже відомим. Тому згадаємо лише основні співвідношення і визначення.
Починаємо з визначення періодичної функції
![]() , (1)
, (1)
де ![]() – постійна величина, названа періодом;
– постійна величина, названа періодом;
![]() – будь-яке ціле число, позитивне чи негативне.
– будь-яке ціле число, позитивне чи негативне.
Визначення (1) виражає основну властивість періодичної функції, яка полягає в тому, що хід явища періодично повторюється, і періодичність ця існує вічно, тобто для всього часу від –![]() до +
до +![]() .
.
З цього відразу можна зробити висновок, що періодичних явищ у точному розумінні визначення (1) немає і бути не може. Періодична функція є корисна математична абстракція.
Будь-яка – з несуттєвими для нас математичними обмеженнями – періодична функція може бути представлена рядом за тригонометричними функціями
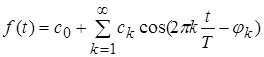 . (2)
. (2)
Періодична функція ![]() представлена таким чином, сумою доданків виду
представлена таким чином, сумою доданків виду ![]() , кожен з яких є синусоїдальне коливання з амплітудою
, кожен з яких є синусоїдальне коливання з амплітудою ![]() і початковою фазою
і початковою фазою ![]() . Значення
. Значення ![]() і
і ![]() мають бути належним чином підібрані для того, щоб рівність (2) виконувалася. Частоти коливань, з яких складається періодична функція
мають бути належним чином підібрані для того, щоб рівність (2) виконувалася. Частоти коливань, з яких складається періодична функція ![]() , утворюють гармонійну послідовність. Це означає, що частоти всіх складових кратні основній частоті
, утворюють гармонійну послідовність. Це означає, що частоти всіх складових кратні основній частоті ![]() . Окремі складові носять назви гармонік. Коливання з частотою
. Окремі складові носять назви гармонік. Коливання з частотою ![]() називається першою гармонікою (
називається першою гармонікою (![]() ), з частотою
), з частотою ![]() – другою гармонікою, і т.д.
– другою гармонікою, і т.д.
Вираз (2) може бути переписаний в інший, дуже вживаній формі
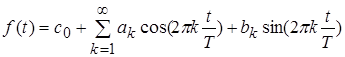 , (3)
, (3)
де
![]() ,
, ![]() ,
,
так що ![]()
![]() ,
, 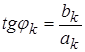 .
.
Коефіцієнти ![]() і
і ![]() визначаються за формулами
визначаються за формулами
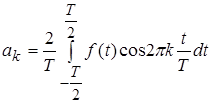 , (4)
, (4)
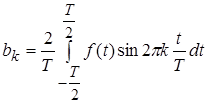 . (5)
. (5)
Величина ![]() виражає середнє значення функції за період, вона називається часто постійною складовою і обчислюється за формулою
виражає середнє значення функції за період, вона називається часто постійною складовою і обчислюється за формулою
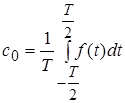 . (6)
. (6)
Чудовою властивістю ряду Фур'є є те, що якщо взяти кінцеве число членів ряду, тобто апроксимувати періодичну функцію тригонометричним поліномом, представивши її у вигляді
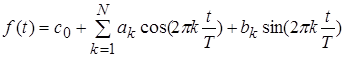 ,
,
то для будь-якого ![]() можна отримати найменше квадратичне відхилення від точного значення
можна отримати найменше квадратичне відхилення від точного значення ![]() , якщо коефіцієнти визначені за формулами (4), (5), (6). Із збільшенням числа членів
, якщо коефіцієнти визначені за формулами (4), (5), (6). Із збільшенням числа членів ![]() наближення, зрозуміло, поліпшується, і в границях при
наближення, зрозуміло, поліпшується, і в границях при ![]() наближена рівність переходить у точну.
наближена рівність переходить у точну.
Ряд Фур'є може бути також записаний у комплексній формі в такий спосіб:
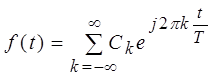 , (7)
, (7)
де
![]() ;
; ![]() ;
; ![]() .
.
Величина 2![]() є комплексна амплітуда, величина
є комплексна амплітуда, величина ![]() знаходиться за формулою
знаходиться за формулою
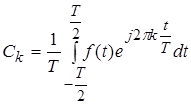 , (8)
, (8)
Підсумовування в (7) ведеться за всіма цілими ![]() , як позитивними, так і негативними, включаючи і нуль. Для того, щоб повернутися від (1) до (2) чи (3), потрібно згадати, що дійсна частина кожного доданка під знаком суми (7) парна стосовно
, як позитивними, так і негативними, включаючи і нуль. Для того, щоб повернутися від (1) до (2) чи (3), потрібно згадати, що дійсна частина кожного доданка під знаком суми (7) парна стосовно ![]() , а уявна частина – непарна. Надалі переважно користуватимемось компактною формою (7).
, а уявна частина – непарна. Надалі переважно користуватимемось компактною формою (7).
Ряд Фур'є дає розкладання періодичної функції за тригонометричними функціями. Це розкладання може бути узагальнено і на випадок неперіодичної функції. Неточний, але наочний шлях до одержання розкладання Фур'є неперіодичної функції полягає в застосуванні граничного переходу при ![]() . Дійсно, неперіодичну функцію можна розглядати як граничний випадок періодичної функції при необмежено зростаючому періоді. Візьмемо формулу (7) і підставимо в неї значення
. Дійсно, неперіодичну функцію можна розглядати як граничний випадок періодичної функції при необмежено зростаючому періоді. Візьмемо формулу (7) і підставимо в неї значення ![]() з (8)
з (8)
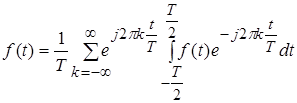 .
.
Перейдемо до границі, спрямовуючи ![]() . Замість
. Замість ![]() введемо кругову основну частоту
введемо кругову основну частоту
![]() .
.
Ця частота є частотним інтервалом між сусідніми гармоніками, частоти яких дорівнюють ![]() . При граничному переході зробимо заміну за такою схемою
. При граничному переході зробимо заміну за такою схемою
![]() ,
, ![]() ,
, ![]() ,
,
де ![]() – поточна частота, що змінюється безупинно;
– поточна частота, що змінюється безупинно;
![]() – її прирощення.
– її прирощення.
Сума перейде в інтеграл, і ми одержимо:
![]() , (9)
, (9)
чи
![]() , (10)
, (10)
де
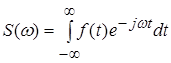 . (11)
. (11)
Формули (10) і (11) є основними формулами теорії спектрів. Вони являють собою пари перетворень Фур'є, що пов'язують між собою дві функції: дійсну функцію часу ![]() і комплексну функцію частоти
і комплексну функцію частоти ![]() . Формула (10) являє собою інтеграл Фур'є в комплексній формі. Зміст цієї формули полягає в тому, що функція
. Формула (10) являє собою інтеграл Фур'є в комплексній формі. Зміст цієї формули полягає в тому, що функція ![]() представлена сумою синусоїдальних складових. Але функція
представлена сумою синусоїдальних складових. Але функція ![]() передбачається неперіодичною, тому вона може бути представлена тільки сумою нескінченно великого числа нескінченно малих коливань, нескінченно близьких за частотою. Комплексна амплітуда кожного окремого коливання нескінченно мала, вона дорівнює
передбачається неперіодичною, тому вона може бути представлена тільки сумою нескінченно великого числа нескінченно малих коливань, нескінченно близьких за частотою. Комплексна амплітуда кожного окремого коливання нескінченно мала, вона дорівнює
![]() . (12)
. (12)
Частотний інтервал між двома сусідніми коливаннями також нескінченно малий; він дорівнює ![]() .
.
Якщо ряд Фур'є являє собою періодичну функцію сумою хоча і нескінченного числа синусоїд, але з частотами, що мають визначені дискретні значення, то інтеграл Фур'є подає неперіодичну функцію сумою синусоїд з безперервною послідовністю частот. У складі неперіодичної функції є всі частоти.
Одна з особливостей, що відрізняє інтеграл Фур'є від ряду Фур'є, полягає в тому, що ряд Фур'є подає періодичну функцію як суму періодичних складових, тоді як інтеграл Фур'є – неперіодичну функцію сумою періодичних складових. Отже, у випадку інтеграла Фур'є сумі не притаманні властивості своїх доданків, і цю обставину необхідно враховувати у міркуваннях загального характеру про спектральне розкладання Фур'є.
Зазначимо насамкінець, що формулу (10) можна записати в дійсній формі; тоді інтегрування проводитиметься тільки по позитивних частотах. Увівши позначення
![]() ,
,
одержимо (з огляду на те, що А – парна, а В – непарна функція)
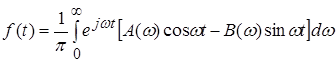 . (13)
. (13)
Можна одержати ще один запис формули (10), подавши її у вигляді
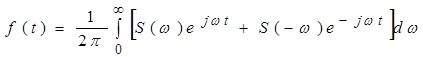 .
.
У квадратних дужках поставлена сума сполучених величин, що дорівнює подвоєній дійсній частині. Тому
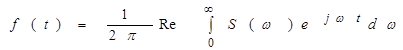 .
.