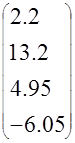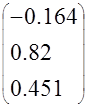| Скачать .docx |
Реферат: Контрольная работа: Расчет цифрового корректора
![]()
Контрольная работа
студентов-заочников по дисциплине
«Цифровая обработка сигналов»
Расчет цифрового корректора
Задан канал передачи дискретных сообщений. Межсигнальная
интерференция сигналов в канале определяется импульсной характеристикой, отсчеты которой равны:
g0![]() g(0)=(-1)
g(0)=(-1)![]() *(m+1)/20
*(m+1)/20
g1![]()
![]() g(t)=1
g(t)=1
g2![]() g(2T)=(-1)
g(2T)=(-1)![]() *(n+1)/20
*(n+1)/20
где m-предпоследняя цифра № зачетной книжки
n-последняя цифра №зачетной книжки
1.Используя выражение дискретной свертки, рассчитать сигнал на выходе канала в отсчетные моменты 0,1,2,3 для последовательности входных сигналов u(0),u(T)
a) u(0)=U, u(T)=0
Где U=n+1
b) u(0)=U, u(T)=U
В другие отсчетные моменты u(2T)=u(3T)=0
2.Рассчитать коэффициенты цифрового корректора C![]() ,C
,C![]() ,C
,C![]() ,обеспечивающие выходной сигнал “010” при подаче на
,обеспечивающие выходной сигнал “010” при подаче на
вход канала сигнала “100”.
3.Рассчитать сигналы на выходе корректора при входных сигналах (a),(b).Проанализировать эффективность работы корректора.
Пример выполнения для m=3,n=10
Отсчеты импульсной характеристики равны
g0=0.2; g1=1; g2= -0.5; U=11
![]()
![]() Задание 1
Задание 1
Пусть u1(kT)-сигал на выходе канала связи (входе корректора)
В соответствии с выражением дискретной свертки он равен
u1(kT)=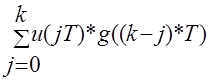 k=0,1,2,3
k=0,1,2,3
Учитывая,что u(jT)=0 для j![]() 1 и g(mT)=0 для m
1 и g(mT)=0 для m![]() 2, получаем
2, получаем
k=0 u1(0)=u(0)*g(0)=u(0)*g0
k=1 u1(T)=u(0)*g(T)+u(T)*g(0)=u(0)*g1+u(T)*g0
k=2 u1(2T)=u(0)*g(2T)+u(T)*g(T)=u(0)*g2+u(T)*g1
k=3 u1(3T)=u(T)*g(2T)=u(T)*g2
Для варианта (а) u(0)=11,u(T)=0
u1(0)=11*0.2=2.2 u1(T)=11*1+0*0.2=11 u1(2T)=11*(-0.55)+0*1=-6.05 u1(3T)0*(-0.55)=0 |
U1=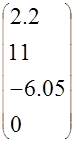 |
Для варианта (б) u(0)=11,u(T)=11
u1(0)=11*0.2=2.2 u1(T)=11*1+11*0.2=13.2 u1(2T)=11*(-0.55)+11*1=4.95 u1(3T)=11*(-0.55)=-6.05 |
U1= |
Задание 2(пояснение)

| t |
0 T 2T
![]() g g1
g g1
![]() 2T
2T
T |
0 T g2
| g1 | g0 | 0 |
| g2 | g1 | g0 |
| g2 | g1 |
![]()
![]()
![]()
![]()
![]() C
C![]()
![]()
![]() С
С![]()
![]()
![]() С
С![]()
![]()
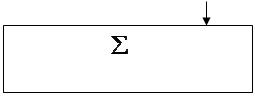 |
![]()
![]()
система из 3-х уравнений Матрица коэф- Вектор Вектор
с 3-мя неизвестными фициентов неизвестного прав.
коэффициента частей
корректора
![]()
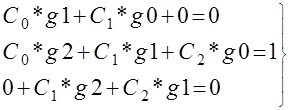 G=
G=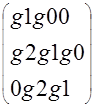
![]() C=
C=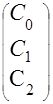 H=
H=![]()
![]()
В векторно-матричной форме G*C=H
 *
*![]() =
=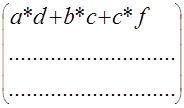
Умножаем слева на обратную матрицу G![]()
![]()
G![]() *G*C= G
*G*C= G![]() *H,откуда С= G
*H,откуда С= G![]() *H,где
*H,где
Умножаем слева на обратную матрицу G![]()
![]()
G![]() *G*C= G
*G*C= G![]() *H, откуда С= G
*H, откуда С= G![]() *H,где
*H,где
(G![]() *G)-единичная матрица
*G)-единичная матрица ![]()
![]()
Решение с помощью системы Mathcad
|
|
|
Введите
Задайте матрицу G:=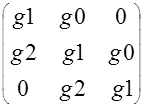 |
Вектор H:= |
||||
Вычислите C:=G |
Рассчитайте |
Решение системы уравнений по формуле Крамера
С![]() =D
=D![]() /D
/D![]() C
C![]() =D
=D![]() /DC
/DC![]() =D
=D![]() /D
/D
где D- определитель матрицы G
D=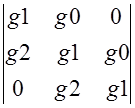 =
=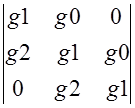
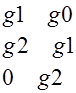 =g1
=g1![]() -g2*g0*g1-g1*g2*g0=
-g2*g0*g1-g1*g2*g0=
=1-2*g0*g2=1-2*0.2*(-0.55)=1.22
D=1.22
D![]() -определитель матрицы G,где 1-й столбец заменен на вектор H
-определитель матрицы G,где 1-й столбец заменен на вектор H
D![]() =
=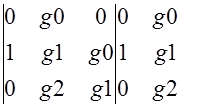 =0-g1*1*g0=-g0=-0.2
=0-g1*1*g0=-g0=-0.2
D![]() -определьтель матрицы G ,где 2-й столбец заменен на H
-определьтель матрицы G ,где 2-й столбец заменен на H
D![]() =
=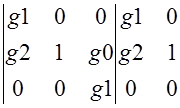 =g1
=g1![]() -0=1
-0=1
D![]() -определитель матрицы G,где 3-й столбец заменен на H
-определитель матрицы G,где 3-й столбец заменен на H
D![]() =
=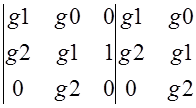 =0-g2*1*g1=0.55
=0-g2*1*g1=0.55
Таким образом, коэффициенты Вектор коэффициентов
корректора равны
С C C |
С=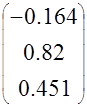 |
|||||
Задание 3 Прохождение сигнала U1(kT) через корректор иллюстрируется схемой: |
||||||
U1(kT |
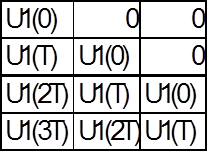 |
V(0)=U1(0)*C V(T)=U1(T)*C V(2T)=U1(2T)*C V(2T)=U1(3T)*C |
||||
![]() C
C![]()
![]()
![]() С
С![]()
![]()
![]()
![]()
![]()
![]() С
С![]()
![]()
V(kT) |
V(0)=2.2*(-0.164)=-0.361 V(T)=11*(-0.164)+2.2*0.82=0 V(2T)=(-0.6.05)* (-0.164)=11*0.82+2.2*0.451=11.004 V(3T)=0*(-0.164)+ (-6.05)*0.82+11*0.451 |
Вектор выходного сигнала
![]()
![]()
![]()
![]() (а) Ожидаемый (б) Ожидаемый
(а) Ожидаемый (б) Ожидаемый
сигнал сигнал
V=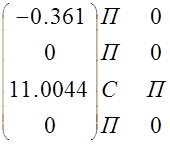
![]() V=
V=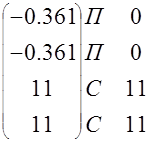
Максимальный модуль разности между ожидаемым и полученным выходным сигналом
(а) (б)
![]()
![]()
![]()
![]() V
V![]() =0,361 V
=0,361 V![]() =0.361
=0.361
![]()
![]()
![]()
![]()
![]()
![]() V
V![]()
![]() 0 V
0 V![]()
![]() 0
0
На выходе корректора:
![]()
![]()
![]()
![]() (а) ожидаемый (б) ожидаемый
(а) ожидаемый (б) ожидаемый
сигнал сигнал
![]()
![]()
![]()
![]()
![]()
![]() U1=
U1=![]()
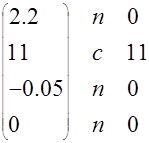 U1=
U1=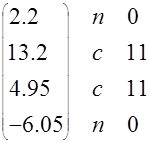
![]()
![]() U1
U1![]() =6.05 U1
=6.05 U1![]() =6.05
=6.05
![]() U1
U1![]() =0 U1
=0 U1![]() =6.05
=6.05
Сопоставление максимальных погрешностей до коррекции и после коррекции:
![]() (а) (б)
(а) (б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() U1
U1![]()
![]() V1
V1![]() U1
U1![]() V1
V1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() U1
U1![]() = V1
= V1![]() U1
U1![]() V1
V1![]()
свидетельствует об эффективной работе корректора.