1.2 Амплитуда ошибки в стационарном режиме при действии эквивалентной синусоиды с заданными максимальными значениями скорости и ускорения воздействия не превышает 5% полуапертуры.

1.3 Максимальное значение ошибки в переходном режиме при скачке скорости воздействия не превышает 50% полуапертуры.

2. Рассчитать параметры сглаживающих цепей из условий:

2.1 Запас устойчивости по фазе не меньше 30°.

2.2 С.К.О. ошибки слежения, вызванной действием помехи с заданным q² _max , не превышает 20% полуапертуры.

3. Рассчитать минимальное значение отношения мощности сигнала к мощности помехи q² _min из условия:

3.1 Вероятности срыва слежения P_ср = 0,05 за время 1000 сек.

Условные обозначения, символы и сокращения

ЧАП – частотная автоподстройка

РА – радиоавтоматика

С.К.О. – среднеквадратическое отклонение

УПЧ – усилитель промежуточной частоты

ЧД – частотный детектор

ФНЧ – фильтр нижних частот

ПГ – перестраиваемый генератор

СМ – смеситель

ЛАХ – логарифмическая амплитудно-частотная характеристика

ФЧХ – фазо-частотная характеристика

Введение

В современных радиотехнических устройствах различного назначения и системах радиоуправления широко применяются автоматические системы, которые называют системами радиоавтоматики. К ним относятся устройства фазовой и частотной автоподстройки частоты, автоматической регулировки усиления, системы измерения координат движущихся объектов, измерители дальности, различные следящие фильтры и другие.

Выделение систем РА в самостоятельный класс обусловлено их особенностями, связанными с условиями работы в составе радиотехнических устройств и систем радиоуправления, в которых осуществляется обработка параметров радиосигнала при действии различного вида помех.

Надежность и качество работы систем РА во многом определяют характеристики радиоаппаратуры и систем радиоуправления.

Рассмотрим систему (ЧАПЧ).

Системы автоматической подстройки частоты применяются в радиоприемных устройствах, доплеровских системах измерения скорости подвижных объектов, устройствах частотной селекции сигналов. На рис. 1 показана упрощенная функциональная схема супергетеродинного приемника, в котором для стабилизации промежуточной частоты сигнала используется система ЧАП.

Система ЧАП, включаемая в состав приемника, работает следующим образом. Напряжение с выхода УПЧ подается на частотный дискриминатор (ЧД). При появлении отклонения промежуточной частоты сигнала от её номинального значения, которое совпадает с центральной частотой УПЧ, на выходе дискриминатора появляется напряжение, зависящее от величины и знака отклонения D w . Выходное напряжение дискриминатора, пройдя через фильтр нижних частот (ФНЧ), поступает на подстраиваемый генератор (ПГ) и изменяет его частоту, а следовательно, и промежуточную частоту сигнала так, что исходное рассогласование D w уменьшается.

В результате работы системы ЧАПЧ промежуточная частота сигнала удерживается близкой к центральной частоте УПЧ. Это позволяет существенно уменьшить влияние взаимной нестабильности частот передатчика и гетеродина, сузить полосу УПЧ и повысить качество приема.

Объектом курсового проектирования является система радиоавтоматики (следящая радиотехническая система), осуществляющая выделение какого-либо параметра радиотехнического сигнала с использованием принципа обратной связи.

Перечень исходных данных и требуемых значений показателей качества формулируются преподавателем – руководителем курсовой работы и может быть различным в зависимости от концепции руководителя.

В качестве исходных данных задается тип следящей радиотехнической системы, порядок ее астатизма, постоянная времени простого инерционного звена, полоса пропускания радиоприемного устройства, максимальное значение отношения мощностей сигнала и помехи на выходе линейной части радиоприемного устройства, форма радиосигнала, используемого в системе, и его параметры, тип обработки – аналоговая или цифровая. В качестве характеристик воздействия фигурируют максимальные значения скорости и ускорения параметра сигнала, за которым следит система.

Целью проектирования является расчет основных параметров системы, удовлетворяющих системе заданных показателей качества. К числу таких показателей относится точность слежения, определяемая значениями и параметрами ошибок слежения, степень устойчивости системы, вероятность срыва слежения за заданное время при заданном относительном уровне помехи и т.д.

1. Расчёт номинального значения петлевого усиления (добротности) К_по

Рассмотрим элементы и математическое описание системы ЧАП.

Преобразование частоты входного сигнала, выполняемое в смесителе (СМ), описывается соотношением:

где w_пр – промежуточная частота сигнала, w_с , w_г – частоты сигнала и подстраиваемого гетеродина соответственно.

Отклонение D w промежуточной частоты сигнала от её номинального значения w_пр0 определяется равенством

При условии безынерционности УПЧ частоты сигналов на его входе и выходе совпадают.

В качестве частотного дискриминатора системы ЧАП используются: частотные детекторы с расстроенными контурами, частотные детекторы с фазовым детектированием и др., которые применяются и для демодуляции частотно-модулированных колебаний.

Выходное напряжение частотного дискриминатора при действии на его входе сигнала и внутреннего шума приемника можно представить в виде суммы математического ожидания и центрированной случайной составляющей:

где – математическое ожидание выходного напряжения, зависящее от расстройки W , также называется дискриминационной характеристикой; x(t, W) – флуктуационная составляющая напряжения u_д (t), W – расстройка промежуточной частоты сигнала по отношению к переходной (центральной) частоте w_п дискриминатора, равная

Качественный характер дискриминационной характеристики показан на рис. 2.

Форма функции F( W), а также характеристики случайного процесса x(t, W) зависят от типа и параметров УПЧ и частотного дискриминатора, отношения сигнал-шум в полосе УПЧ, наличия и характера флуктуаций сигнала и от других факторов. При малых рассогласованиях W дискриминационная характеристика линейна , где S_Д – крутизна дискриминационной характеристики.

Фильтр нижних частот, включаемый на выходе частотного дискриминатора, является, как правило, линейным устройством и описывается линейным дифференциальным уравнением. При использовании однозвенного RC‑фильтра его операторный коэффициент передачи имеет вид

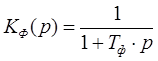Структура, то есть вид, операторного коэффициента передачи К_Ф (р), и параметры фильтра нижних частот системы ЧАП зависят от её назначения. В системах частотной автоподстройки вещательных приемников обычно используют RC-фильтры. Их постоянная времени Т_Ф обычно выбирается так, чтобы на выход фильтра проходили медленные изменения выходного напряжения дискриминатора, вызванные уходами промежуточной частоты сигнала. Флуктуационная составляющая выходного напряжения дискриминатора, а также составляющая этого напряжения, вызванная амплитудной и частотной модуляцией сигнала полезным сообщением, должны подавляться в фильтре.

Изменение частоты подстраиваемого генератора достигается подключением к контуру генератора управляющего элемента, обладающего регулируемым реактивным сопротивлением. В качестве такого элемента может использоваться, например, варикап. Простейшая схема подключения варикапа к контуру генератора показана на рис. 3.

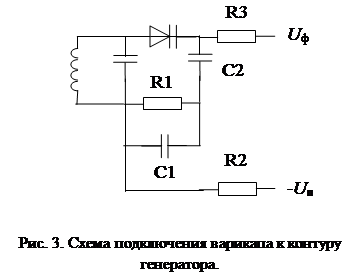
Емкость варикапа регулируется напряжением U_Ф , снимаемым с выхода фильтра нижних частот системы. Напряжение, поступающее с делителя, образованного резисторами R₁ и R₂ обеспечивает запирание диода, как при отрицательных, так и при положительных значениях напряжения U_Ф . Конденсаторы C₁ , C₂ являются блокировочными.

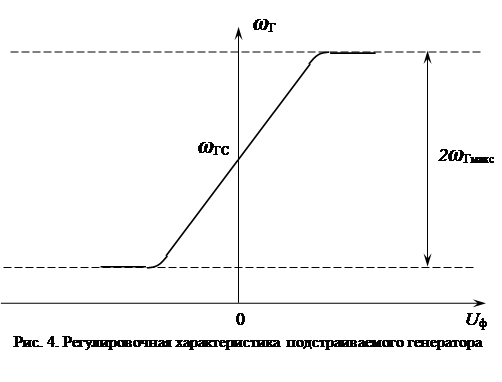
На рис. 4 приведена регулировочная характеристика подстраиваемого генератора. При малых величинах напряжения U_Ф регулировочная характеристика линейна и описывается выражением

где S_P – крутизна регулировочной характеристики, w_ГС – значение собственной частоты генератора при отсутствии управляющего напряжения.

В соответствии с исходными данными структурная схема ЧАП имеет вид, представленный на рис. 5.

Выбор петлевого коэффициента передачи (добротности) системы.

Петлевой коэффициент выбирается из трех условий, два из которых относятся к стационарному режиму. По первому условию необходимо обеспечить величину динамической ошибки при воздействиях, обеспечивающих постоянное значение ошибки в стационарном режиме: включение линейно меняющегося воздействия. Необходимое значение коэффициента передачи находится с помощью формулы:

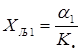где a₁ – параметр воздействия, Х_д1 – динамическая ошибка в системе (). Отсюда получаем:

Второе условие требует выбора петлевого усиления таким образом, чтобы амплитуда ошибки, вызванной действием гармонического воздействия , не превышала заданного значения. При этом амплитуда L_м эквивалентного динамического воздействия и его частота W определяются из системы уравнений:

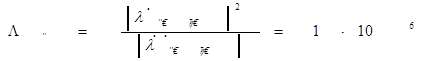где – производная воздействия по времени (скорость воздействия), – вторая производная (ускорение) воздействия по времени.

Амплитуда ошибки слежения Х_м в стационарном режиме может быть найдена из выражения

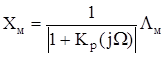где К_р (j w) – комплексный коэффициент передачи системы в разомкнутом состоянии на произвольной частоте w.

При правильном выборе параметров системы амплитуда ошибки Х_м должна быть значительно ниже амплитуды воздействия L_м . Очевидно, что в этом случае должно выполняться неравенство |1+К_р (jw)| >> 1, что возможно при условии |К_р (jw)| >> 1.

Отсюда можно получить приближенное выражение

В соответствии с исходными данными комплексный коэффициент передачи системы в разомкнутом состоянии выглядит следующим образом:

где K_p1 (j w) – комплексный коэффициент передачи системы, Т – постоянная времени простого инерционного звена, входящего в систему в соответствии с заданием на работу.

Далее можно получить неравенство

где K_п – петлевой коэффициент передачи системы.

Отсюда получаем, К_ПГр равен

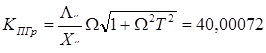При подборе коэффициента передачи по третьему условию необходимо учитывать зависимость от него максимального значения ошибки слежения в переходном режиме, но для получения этой зависимости параметры системы должны быть известными, т.е. ее разработка в линейном приближении завершена, в том числе выполнен синтез цепей коррекции. Следовательно, должна быть завершена работа, требующая знания петлевого усиления. Поэтому здесь используется приближенная формула:

()

Примем коэффициент передачи K_п0 равным 50. Тогда с учетом заданного соотношения мощности сигнала к мощности помехи коэффициент передачи будет равен: .

Построим ЛАХ и ФЧХ системы. Логарифмическая амплитудно-частотная характеристика описывается следующим выражением:

, где .

Фазо-частотная характеристика определяется из равенства:

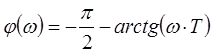Логарифмическая амплитудно-частотная характеристика и фазо-частотная характеристики системы представлены в прил. 1.

Частота среза равна:

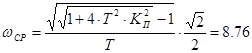(рад/с).

2. Коррекция системы

2.1 Анализ устойчивости системы по фазе

Запас устойчивости системы по фазе:

Полученный запас устойчивости по фазе не удовлетворяет требованиям задания на курсовую работу – запас устойчивости по фазе не меньше 30º. Исходя из этого необходимо включить в систему корректирующее звено, а именно форсирующее звено . Тогда передаточная функция системы примет вид:

Положим τ = 0.08 с. Далее для оценки влияния корректирующего звена необходимо построить логарифмическую амплитудно-частотную и фазо-частотную характеристики. Логарифмическая амплитудно-частотная характеристика данной системы будет описываться выражением:

, где .

Фазо-частотная характеристика определяется из равенства:

Логарифмическая амплитудно-частотная характеристика и фазо-частотная характеристики системы с корректирующим звеном представлены в прил. 2.

Частота среза равна:

(рад/с).

Исходя из этого, запас устойчивости по фазе определяется как:

Таким образом, путём введения в систему корректирующего (в данном случае форсирующего) звена удалось обеспечить требуемый запас устойчивости по фазе (согласно заданию на курсовую работу запас устойчивости по фазе должен быть не менее 30º).

2.2 Расчёт среднеквадратического отклонения ошибки слежения

Зависимость ошибки слежения от времени является случайным процессом, если, по крайней мере, одно из воздействий на систему является случайным процессом. Чаще всего таким воздействием является помеха, поступающая в приемное устройство в сумме (аддитивной смеси) с полезным сигналом, за изменениями одного или нескольких параметров которого следит разрабатываемая система. Указанная помеха может быть внутренним шумом приемного устройства или внешней помехой как естественного, так и искусственного происхождения. Чаще всего в реальных ситуациях помеха является суммой внутреннего шума приемного устройства и разнообразных процессов, источниками которых могут быть космические объекты (шумы космоса, солнца), земная поверхность (тепловое излучение поверхности земли, строений и сооружений), разнообразные промышленные и транспортные установки, генераторы радиосигналов, использующиеся в других радиосистемах, в том числе и специально созданных для противодействия разрабатываемой системе.

Задача помехоустойчивости – обеспечение нормальной работы системы в присутствии радиопомех – главным образом решается дискриминатором путем использования временной, частотной и пространственной селекции полезного сигнала при его приеме в присутствии помех. Однако, как указывалось выше, рациональное использование сглаживающих цепей также может принести ощутимый вклад в повышение помехоустойчивости системы.

Для расчета дисперсии ошибки, вызванной действием помех, необходимо знание статистического эквивалента дискриминатора – его дискриминационной и флуктуационной характеристики. Первая является зависимостью математического ожидания напряжения на выходе дискриминатора от ошибки слежения, а вторая – зависимостью интенсивности помехи на выходе дискриминатора от ошибки слежения. В целом напряжение на выходе дискриминатора U_Д ( t) имеет вид:

U_д (t) = F(x) + n(t),

где Х – ошибка слежения, n( t) – помеха на выходе дискриминатора, F( x) = < U_д ( t)>| _x – условное математическое ожидание напряжения U_Д ( t) при фиксированном Х( t).

При небольших вариациях D x( t) ошибки слежения относительно динамической x_д ( t), можно записать:

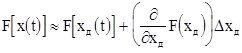где при – коэффициент передачи (крутизна характеристики) дискриминатора в точке x=x_д .

При изменениях динамической ошибки x_д (t) коэффициент передачи дискриминатора также является функцией времени. В случае приблизительно постоянной динамической ошибки или при нахождении всей ошибки x(t) на линейном участке дискриминационной характеристики можно полагать К_д постоянной величиной.

Тогда для расчета дисперсии флуктуационной составляющей ошибки слежения можно воспользоваться частотным методом

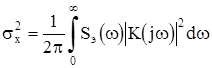где S_э ( w) = S_n ( w)/ K_Д ² – спектральная плотность мощности помехи n( t), пересчитанной на вход дискриминатора (спектральная плотность эквивалентной помехи),

– комплексный коэффициент передачи замкнутой следящей системы.

При слабой зависимости S_э ( w) от частоты w в пределах полосы пропускания замкнутой следящей системы можно полагать , вынести ее из под интеграла и получить:

s_х ² » S_э ×DF_э где S_э =S_n (0)/K_Д ² , 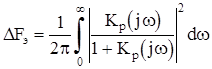– эквивалентная шумовая полоса линеаризованной следящей системы.

Вычисление интеграла в равенстве можно выполнить, используя формулы, приведенные в учебнике [3]. Подынтегральное выражение в можно представить в виде квадрата модуля дробно-рациональной функции

В этом случае результат интегрирования зависит от значений коэффициентов c_к и d_к , а также от порядка системы n . Для систем второго порядка в [3] приведено выражение:

для n=2.

Для

следует, что с₀ = К_П , с₁ = К_П τ, d₀ = K_П , d₁ = (1 + K_П τ), d₀ = Т. Таким образом:

(Гц).

Выражение для шумовой полосы имеет вид (Гц). Тогда спектральная плотность эквивалентной шумовой помехи равна:

Исходя из этого, можно определить среднеквадратическое отклонение ошибки слежения:

(Гц).

По полученным результатам можно сделать вывод, что среднеквадратическое отклонение ошибки слежения удовлетворяет требованиям задания на курсовую работу, поскольку оно (а точнее его квадрат) не превосходит 20% полуапертуры (0.2Δ f = 1000 Гц ), следовательно, нет необходимости в дополнительно коррекции системы.

3. Исследование срыва слежения

Для расчёта минимального значения отношения мощности сигнала и помехи q² _mi _n по критерию равенства вероятности срыва слежения Р_ср = 0,05 за время слежения 1000 с в данной курсовой работе используется метод теории выбросов. В соответствии с ним вероятность срыва слежения отождествляется с вероятностью пересечения изображающей точкой границы апертуры дискриминатора – вероятностью выброса реализации за пределы апертуры дискриминатора. При использовании ряда допущений, справедливых при малых вероятностях срыва слежения, значение последней может быть найдено из приближенного равенства

где m_x – математическое ожидание ошибки слежения, – дисперсия ошибки слежения линеаризованной системы,

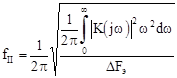– среднеквадратичное значение полосы пропускания следящей системы с коэффициентом передачи К ( j w) в замкнутом состоянии.

Линеаризованная дискриминационная характеристика дискриминатора описывается крутизной S_Д , равной K_П , и представлена на рис. 6.

Следующие математические выкладки необходимы для получения зависимости вероятности срыва слежения о величины отношения мошности сигнала и шума.

Граница апертуры:

Ошибка слежения F определяется из соотношения:

(Гц).

Эквивалентная спектральная полоса помехи:

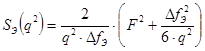Шумовая полоса системы:

, где

Среднеквадратичная полоса пропускания замкнутой системы с коэффициентом передачи K (j w):

, где .

Дисперсия ошибки слежения линеаризованной системы и математическое ожидание ошибки слежения:

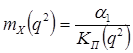Вероятность срыва слежения:

В связи с тем, что зависимость вероятности срыва слежения от отношения q² мощностей сигнала и помехи имеет сложный характер, непосредственное вычисление q² _мин , соответствующего заданному значению P_ср , возможно применением численных методов решения алгебраических уравнений высокого порядка. В данной работе такое уравнение решается графическим методом.

По графику определяем .

Заключение

В данной курсовой работе были рассчитаны основные параметры системы ЧАП. Параметры системы удовлетворяют показателям качества, оговоренным в задании на курсовую работу. Рассчитанная система обладает следующими свойствами: коэффициент петлевого усиления K_П0 = 50. С учетом того, что на входе действует помеха, К_П = 46,87 . При этом динамическая ошибка слежения X_Д = 200 Гц , что меньше, чем максимально допустимое значение 250 Гц . В систему введена цепь коррекции – форсирующее звено с постоянной времени τ = 0.08 с. Необходимость ведения корректирующего звена была вызвана тем, что исходная система не удовлетворяла требованиям устойчивости, оговорённым в задания на курсовую работу (запас устойчивости по фазе – не меньше 30º ). В результате коррекции система имеет следующие параметры: дисперсия ошибки слежения -7.3 Гц , запас устойчивости по фазе 42,27º. По результатам расчета можно составить структурную схему системы АПЧ:

Библиографический список

1. Астрельцов Д.В. Системы радиоавтоматики: методические указания к выполнению курсовой работы по дисциплине «Теория управления и радиоавтоматика» – Екатеринбург: Издательство УГТУ, 1997 – 36 с.

2. Стандарт предприятия. Общие требования и правила оформления дипломных и курсовых проектов (работ). СТП УГТУ-УПИ 1-96. Екатеринбург, 1996.

3. Коновалов Г.Ф. Радиоавтоматика: Учебник для вузов по спец. «Радиотехника». – М.: Высш. шк., 1990.

4. Радиоавтоматика: учебник для вузов / Первачев С.В. – М.: Радио и связь, 1982. 296 с