| Скачать .docx |
Реферат: Электрический расчет несимметричных проволочных антенн
КАЛИНИНГРАДСКИЙ ПОГРАНИЧНЫЙ ИНСТИТУТ
ФЕДЕРАЛЬНОЙ СЛУЖБЫ БЕЗОПАСНОСТИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
![]()
Кафедра №15
КУРСОВАЯ РАБОТА
по дисциплине : «Устройства СВЧ и антенны»
на тему : «Электрический расчет несимметричных проволочных антенн»
Выполнил : к-т 236 уч. гр.
ЛепехоД. В.
Проверил : п-р Волхонская Е.В.
Калининград-2007.
Содержание:
1.1 Задание на курсовую работу
2.1 Эскиз антенны
2.2 Расчёт статической ёмкости антенны по методу Хоу. Расчёт волнового сопротивления антенны
2.3 Расчёт эквивалентной длины антенны lэ для Г-образной антенны
2.4 Расчёт собственной длины волны антенны ![]()
2.5 Расчёт параметров антенны
2.5.1 Расчет действующей длины антенны hд
2.5.2 Расчет сопротивления излучения R∑
2.5.3 Расчет сопротивления потерь Rп
2.5.4 Расчет коэффициента полезного действия антенны
2.5.5 Расчет активной Rа и реактивной Xа составляющих входного сопротивления антенны
2.5.6 Расчет характеристики направленности антенны в вертикальной плоскости и построение диаграммы направленности антенны
2.5.7 Расчет распределения тока и напряжения вдоль вертикальной и горизонтальной части антенны
3.1 Список использованной литературы
1.1 Задание на курсовую работу:
Вариант задания на выполнение курсовой работы
| № Вар | Тип антенны | Вертикальная часть | Горизонтальная часть | Тип провода | Мощность передатчика (Вт) | ||||
| Высота (м) | n | d,м | Длина (м) | n | d, м | ||||
| 55 | Г обр | 4 | 6 | цилиндр (D=0,4) |
7 | 6 | цилиндр (D=0,4) |
ПАБ-16 | 400 |
В процессе выполнения курсовой работы должны быть приобретены навыки инженерного расчета несимметричных антенн и закреплены основы сведения из теории антенн.
К расчёту статической ёмкости антенны и погонного сопротивления по методу Хоу:
Функциональная зависимость коэффициента m1
=f(l/l`
) для определения потенциала горизонтальной части антенны от зарядов вертикальной части. Здесь l – длина провода, потенциал которого отыскиваем; l`
- длина провода, наводящего потенциал. Данные таблицы, приведённой ниже, соответствуют антеннам, у которых угол между вертикальной и горизонтальной частями антенны составляют ![]() . Для Г-образной антенны следует брать отношение l/l`
равным отношению длины горизонтальной части к длине вертикальной части.
. Для Г-образной антенны следует брать отношение l/l`
равным отношению длины горизонтальной части к длине вертикальной части.
| l/l` | 0.2 | 0.4 | 0.6 | 0.7 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 6 |
| m1 | 3.31 | 2.62 | 2.23 | 2.13 | 1.96 | 1.75 | 1.42 | 1.2 | 0.94 | 0.77 | 0.58 |
Для Г-образной антенны расчёт параметров производится на фиксированных частотах, предназначенных для радиослужбы на подвижных объектах (410,425,454,468,480,500,512 кГц)
2.1 Эскиз антенны:
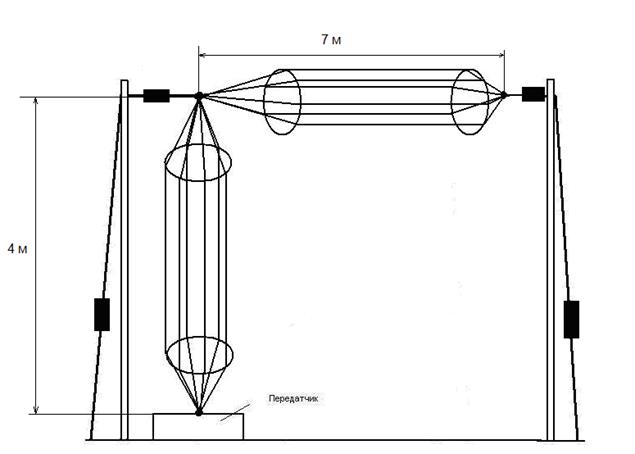
2.2.1. Расчёт статистической ёмкости горизонтальной части:
lv- длина вертикальной части;
b- длина горизонтальной части;
S - площадь поперечного сечения провода;
В - постоянный коэффициент, зависящий от числа лучей;
ng - число проводов в горизонтальной части;
dg - расстояние между проводами в горизонтальной части;
m1 - коэффициент для горизонтальной части.
2.2.1.1. Определяем потенциал горизонтальной части, от собственных зарядов:
2.2.1.2. Находим потенциал в горизонтальной части от зарядов собственного изображения:
2.2.1.3. Определяем потенциал горизонтальной части от зарядов вертикальной части:
2.2.1.4. Рассчитываем потенциал горизонтальной части от зарядов зеркального изображения вертикальной части:
2.2.1.5. Определяем полный потенциал горизонтальной части:
2.2.1.6. Определяем полную статистическую ёмкость горизонтальной части с учётом влияния окружающих металлических масс:
2.2.1.7. определяем погонную емкость горизонтальной части:
2.2.2. Расчёт статической ёмкости вертикальной части антенны:
hv - высота вертикальной части;
m1 - коэффициент для вертикальной части;
hg - высота над которой находится вертикальная часть антенны;
dv - расстояние между проводами в вертикальной части.
2.2.2.1. Определяем потенциал вертикальной части от собственных зарядов:
2.2.2.2. Находим потенциал в вертикальной части от зарядов собственного изображения:
2.2.2.3. Определяем потенциал вертикальной части от зарядов вертикальной части:
2.2.2.4. Рассчитываем потенциал вертикальной части от зарядов зеркального изображения горизонтальной части:
2.2.2.5. Определяем полный потенциал вертикальной части:
2.2.2.6. Определяем полную статистическую ёмкость вертикальной части с учётом влияния окружающих металлических масс:
2.2.2.7. Определяем погонную ёмкость вертикальной части:
2.2.3. Расчёт полной статической ёмкости антенны:
2.2.4 Расчёт волнового сопротивления антенны:
Результаты вычислений сведём в таблицу 1.
| Частота (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| k | 0,0086 | 0,0089 | 0,0095 | 0,0098 | 0,0101 | 0,0105 | 0,0107 |
| ρг (Ом) | 277 | 276 | 274 | 273 | 273 | 271 | 271 |
| ρв (Ом) | 272 | 271 | 269 | 268 | 268 | 266 | 266 |
| ρа (Ом) | 550 | 548 | 544 | 542 | 540 | 538 | 537 |
таблица 1
где:
λ - длины волн на которых производим вычисления;
к - волновое число;
ρг - волновое сопротивление горизонтальной части;
ρв - волновое сопротивление вертикальной части;
ρа - волновое сопротивление всей антенны.
Зависимость полного волнового сопротивления антенны от частоты представлена на рисунке 1:
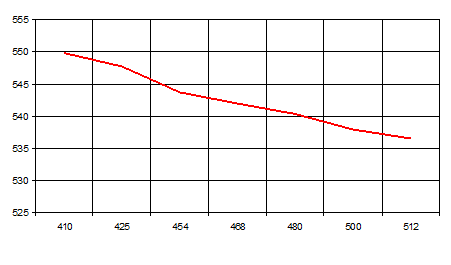
рис. 1 График зависимости полного волнового сопротивления антенны от частоты
2.3. Расчёт эквивалентной длины антенны lэ для Г-образной антенны:
С помощью горизонтальной части получаем более равномерное распределение тока вдоль вертикальной части, а значит увеличили действующую длину и увеличили мощность излучения. Горизонтальную часть заменяем на эквивалентный отрезок провода, присоединяемый к вертикальной части, длина которого bэ выбирается таким образом, чтобы реактивное сопротивление данного отрезка и горизонтальной части в месте стока были равны друг другу. Расчёт проводим на фиксированных частотах, предназначенных для радиослужбы на подвижных объектах (410,425,454,468,480,500,512 кГц).
Результаты вычислений представим в таблице 2.
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| к | 0,0086 | 0,0089 | 0,0095 | 0,0098 | 0,0101 | 0,0105 | 0,0107 |
| bэ (м) | 1,5106 | 1,5107 | 1,5107 | 1,5108 | 1,5108 | 1,5108 | 1,5109 |
| lэ (м) | 5,5106 | 5,5107 | 5,5107 | 5,5108 | 5,5108 | 5,5108 | 5,5109 |
таблица 2
где:
bэ - эквивалентная длина горизонтальной части антенны, вычисляемая по формуле ![]()
lэ - эквивалентная длина горизонтальной части антенны (lэ=lv+bэ).
Зависимость эквивалентной длины от частоты представлена на рисунке 2:
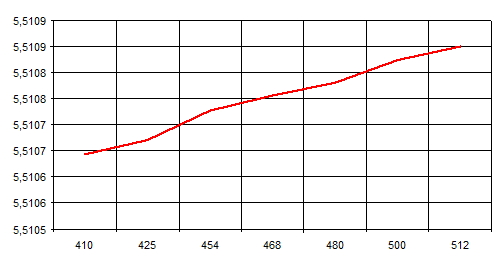
рис. 2 График зависимости эквивалентной длины антенны от частоты
Из графика видно, что при увеличении частоты эквивалентная длина антенны увеличивается. Следовательно, если мы хотим, что бы наша антенна работала на более высоких частотах, необходимо увеличивать длину горизонтальной части антенны.
2.4. Расчёт собственной длины волны антенны:
Наибольшая волна, при которой антенна настроена в резонанс, обычно называется собственной волной антенны. Из первой таблицы выбираем наибольшую lэ. Для данной эквивалентной длине антенны произведём расчёт собственной длины волны этой антенны:
Результаты вычислений собственной длины представим в таблице 3.
| λ (м) | 20 | 24 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| к | 0,3142 | 0,2618 | 0,2094 | 0,1795 | 0,1571 | 0,1396 | 0,1257 | 0,1142 | 0,1047 | 0,0967 | 0,0898 |
| tg (klv) | 3,0777 | 1,7321 | 1,1106 | 0,8737 | 0,7265 | 0,6249 | 0,5498 | 0,4917 | 0,4452 | 0,4072 | 0,3753 |
| W | 0,2952 | 0,4446 | 0,6435 | 0,7974 | 0,9454 | 1,0896 | 1,2312 | 1,3709 | 1,5093 | 1,6466 | 1,7831 |
таблица 3
где:
![]()
![]()
![]()
Графическое решение представлено на рисунке 3:
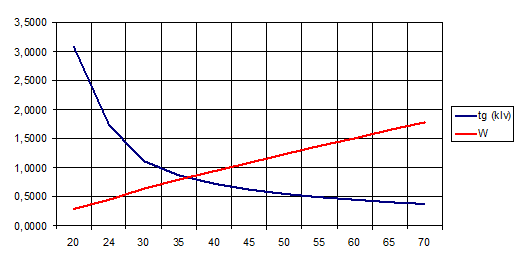
рис. 3 График расчёта собственной длины волны
Из построенных графиков видим, что собственная длина волны 36 м.
Увеличение длины собственной волны я является одной из причин использования заземлённых антенн на длинных и средних волнах.
2.5. Расчёт параметров антенны:
2.5.1. Расчёт действующей высоты антенны:
Действующая длина (высота) - это коэффициент пропорциональности между напряжённостью поля в направлении максимального излучения током рассматриваемой в антенне. Определим действующую высоту для семи фиксированных частот. Результаты вычислений представим в виде таблицы 4:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| к | 0,0086 | 0,0089 | 0,0095 | 0,0098 | 0,0101 | 0,0105 | 0,0107 |
| bэ (м) | 1,5106 | 1,5107 | 1,5107 | 1,5108 | 1,5108 | 1,5108 | 1,5109 |
| lэ (м) | 5,5106 | 5,5107 | 5,5107 | 5,5108 | 5,5108 | 5,5108 | 5,5109 |
| hд (м) | 2,5487 | 2,5487 | 2,5488 | 2,5489 | 2,5489 | 2,5490 | 2,5490 |
таблица 4
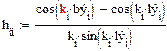 |
где:
Зависимость действующей длины от частоты представлена на рисунке 4:
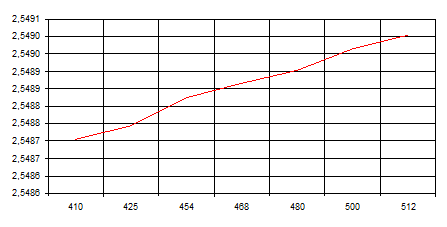
рис. 4 График зависимости действующей длины антенны от частоты
Из построенного графика видно, что с увеличением рабочей частоты действующая высота антенны увеличивается. Разница между максимальной и минимальной рабочими частотами составляет не более 100 кГц, но на эту разницу действующая дина антенны изменилась всего на 0,0003 метра, что составляет незначительные изменения, следовательно, антенна будет нормально работать и при изменении частоты на более большое значение. Но при увеличении частоты этот параметр стабильно увеличивается, что для нашей антенны благоприятно. следовательно, увеличение частоты не окажет отрицательного влияния на этот параметр антенны.
2.5.2. Расчёт сопротивления излучения:
Основное излучение в несимметричных антеннах приходится на вертикальную часть. Роль горизонтальной части заключается в том, что она даёт более равномерное распределение тока в антенне, увеличивает ёмкость антенны и уменьшает напряжение в ней.
Произведём расчёт сопротивления излучения антенны для семи фиксированных частот. Так как наша антенна обладает эквивалентной длиной меньше, чем значение 0,3![]() , то воспользуемся следующей формулой для определения сопротивления излучения.
, то воспользуемся следующей формулой для определения сопротивления излучения.
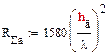 |
Вычисления сведём в таблицу 5:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| hд (м) | 2,5487 | 2,5487 | 2,5488 | 2,5489 | 2,5489 | 2,549 | 2,549 |
| R∑а(Ом) | 0,0192 | 0,0206 | 0,0235 | 0,0250 | 0,0263 | 0,0285 | 0,0299 |
таблица 5
Зависимость сопротивления излучения антенны от частоты представлена на рисунке 5:
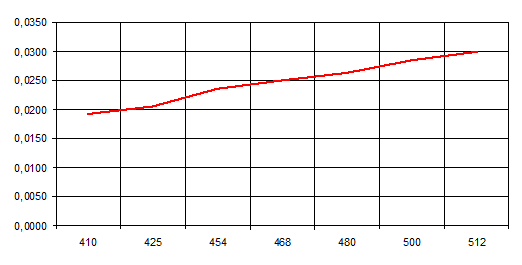
рис. 5 Зависимость сопротивления излучения антенны от частоты
Из построенного графика видно, что при увеличении рабочей частоты, сопротивление излучения увеличивается, следовательно антенна сможет работать в этом диапазоне, так как коэффициент её полезного действия будет постоянно увеличиваться.
2.5.3. Расчёт сопротивления потерь:
Потери энергии в антенной цепи на ДВ и СВ диапазонах складываются:
1. из потерь и в заземлении или противовесе;
2. потерь в органах настройки;
3. потерь в изоляторах и проводах;
4. прочие антенны (мачты, оттяжки).
Самые большие потери в органах настройки с удлинением длины волны. Рассчитаем сопротивление потерь на семи фиксированных частотах. Результаты вычислений представлены в таблице 6:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| Rп (Ом) | 49,80 | 48,04 | 44,97 | 43,63 | 42,53 | 40,83 | 39,88 |
таблица 6
где:
Зависимость сопротивления потерь от частоты представлена на рисунке 6:
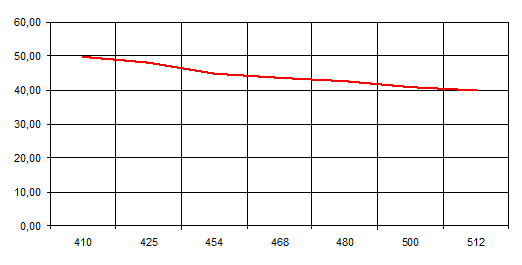
рис. 6 График зависимости сопротивления потерь антенны от частоты.
Из построенного графика видно, что с увеличением частоты сопротивление потерь уменьшается. Значит на более высоких частотах антенна будет годна к использованию, так как её коэффициент полезного действия будет возрастать.
2.5.4. Расчёт коэффициента полезного действия:
Найдём коэффициент полезного действия нашей антенны на семи фиксированных частотах, результаты в таблице 7:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| Rп (Ом) | 49,80 | 48,04 | 44,97 | 43,63 | 42,53 | 40,83 | 39,88 |
| R∑а (Ом) | 0,0192 | 0,0206 | 0,0235 | 0,025 | 0,0263 | 0,0285 | 0,0299 |
| КПД | 0,04 | 0,04 | 0,05 | 0,06 | 0,06 | 0,07 | 0,07 |
таблица 7
где:
- коэффициент полезного действия
Зависимость КПД антенны от частоты представлена на рисунке 7:
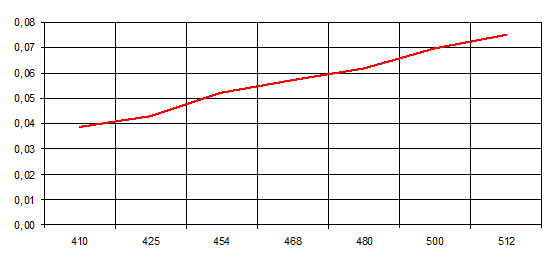
рис. 7 График зависимости КПД антенны от частоты
Из полученного графика видно, что при увеличении частоты коэффициент полезного действия антенны увеличивается. Следовательно нашу антенну целесообразно использовать на более высоких частотах.
2.5.5. Расчёт активной и реактивной составляющих входного сопротивления антенны:
Активное сопротивление антенны складывается из сопротивлений излучения и потерь (![]() ). Таким образом активное сопротивление антенны на семи фиксированных частотах будет равно, расчёты представлены в таблице 8:
). Таким образом активное сопротивление антенны на семи фиксированных частотах будет равно, расчёты представлены в таблице 8:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| Rп (Ом) | 49,80 | 48,04 | 44,97 | 43,63 | 42,53 | 40,83 | 39,88 |
| R∑а (Ом) | 0,0192 | 0,0206 | 0,0235 | 0,025 | 0,0263 | 0,0285 | 0,0299 |
| Rа (Ом) | 49,82 | 48,06 | 44,99 | 43,65 | 42,56 | 40,86 | 39,91 |
таблица 8
Зависимость активного входного сопротивления антенны от частоты представлена на рисунке 8:

рис. 8 График зависимости активного входного сопротивления антенны от частоты
Из графика видно, что при увеличении частоты активное сопротивление уменьшается, следовательно при увеличение частоты коэффициент полезного действия будет увеличиваться. И целесообразно использовать нашу антенну на приём и на передачу.
Реактивное сопротивление нашей антенны носит ёмкостной характер ![]() . В этом случае реактивное сопротивление антенны рассчитываем по следующей формуле:
. В этом случае реактивное сопротивление антенны рассчитываем по следующей формуле:
![]()
![]()
Результаты вычислений сведены в таблицу 9:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| к | 0,0086 | 0,0089 | 0,0095 | 0,0098 | 0,0101 | 0,0105 | 0,0107 |
| lэ (м) | 5,5106 | 5,5107 | 5,5107 | 5,5108 | 5,5108 | 5,5108 | 5,5109 |
| ρв (Ом) | 272 | 271 | 269 | 268 | 268 | 266 | 266 |
| Xa (Oм) | -3323,16 | -3193,52 | -2966,46 | -2866,5 | -2794,42 | -2661,93 | -2599,09 |
таблица 9
На рисунке 9 представлена зависимость реактивного сопротивления антенны от частоты:
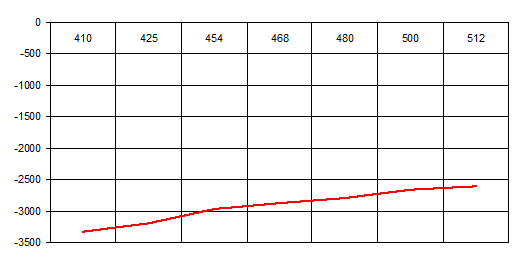
рис. 9 График зависимости реактивного сопротивления антенны от частоты
Из полученного графика видно, что при увеличении частоты реактивное сопротивление стремится к нулю, что для нашей антенны благоприятно, так как остаётся одно активное сопротивление. Так как реактивное сопротивление носит ёмкостной характер, то рекомендуется включить для настройки антенны в резонанс, необходимо ввести элемент настройки виде индуктивности, с переменной индуктивностью ![]() ;
; ![]() ;
; ![]() .
.
Произведём расчёт индуктивности на семи фиксированных частотах, результаты представим в виде таблицы 10:
| f (кГц) | 410 | 425 | 454 | 468 | 480 | 500 | 512 |
| λ (м) | 731,707 | 705,882 | 660,793 | 641,026 | 625,000 | 600,000 | 585,938 |
| Xa (Oм) | -3323,16 | -3193,52 | -2966,46 | -2866,5 | -2794,42 | -2661,93 | -2599,09 |
| Lн (Гн) | 0,001290 | 0,001196 | 0,001040 | 0,000975 | 0,000927 | 0,000847 | 0,000808 |
таблица 10
Зависимость переменной индуктивности от частоты представлена на рисунке 10:
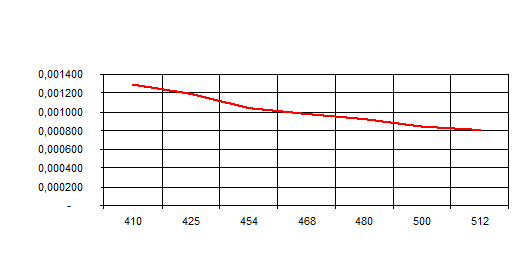
рис. 10 График зависимости переменной индуктивности от частоты
С увеличением частоты Lуменьшается, следовательно, чтобы не подбирать катушку индуктивности на каждой частоте, её следует сделать переменной.
2.5.6 Расчет характеристики направленности антенны в вертикальной плоскости и построение диаграммы направленности антенны:
На ДВ и СВ земля по своим свойствам является хорошим проводником и её действие на ДН можно учесть влияние зеркального изображения с тем же направлением тока равной величины. Следовательно, замена земли зеркальным изображением вибратора сводится к переходу от симметричного вертикального вибратора длиной lэ к симметричному длиной 2lэ. Поэтому ДН такого вибратора в вертикальной плоскости выражается формулой:
В соответствии с данными значениями построим диаграмму направленности Г-образной антенны, на боковых и средней частотах (410; 468; 512 кГц). На рисунке 11 представлена диаграмма направленности для f=410 кГц:
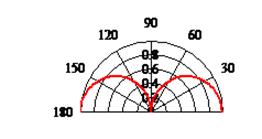 |
рис. 11 Диаграмма направленности Г-образной антенны
На рисунке 12 представлена диаграмма направленности для f=468 кГц:
 |
рис. 12 Диаграмма направленности Г-образной антенны
На рисунке 13 представлена диаграмма направленности для f=512 кГц:
 |
рис. 13 Диаграмма направленности Г-образной антенны
Анализ данной диаграммы направленности показывает, что имеются два направления максимально излучения 0 и 180 градусов в меридиональной плоскости и одно направление минимального излучения в 90 градусов, по всем другим направлениям происходит уменьшение амплитуды до нуля.
Можно проследить, что при уменьшении длины волны диаграмма направленности сужается, но незначительно, так как все длины волн соизмеримы с длиной вибратора.
2.5.7. Расчёт распределения тока и напряжения вдоль антенны:
Все расчёты распределения тока и напряжения вдоль антенны производим на одной частоте равной 500 кГц.
2.5.7.1. Определяем действующее и амплитудное значение тока в основании антенны:
где:
Р0 - мощность передатчика (400 Вт);
- КПД антенны;
- КПД согласующего устройства;
- добротность антенны;
- добротность согласующего устройства;
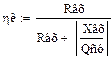 |
- КПД фидера;
- КПД согласующего устройства
- входное сопротивление антенны;
2.5.7.2. Определяем амплитудное значение напряжение на изолированном конце Г-образной антенны:
2.5.7.3. Распределение тока вдоль вертикальной части антенны определятся выражением:
zv - меняется от 0 до 4 м - конца вертикальной части антенны;
Ipv - ток в пучности, равен:
Таким образом расчёт распределение тока вдоль вертикальной части антенны представим в табличном виде, таблица 11:
| zv (м) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| lv (А) | 3,3376 | 3,0351 | 2,7325 | 2,4298 | 2,1270 | 1,8242 | 1,5213 | 1,2184 | 0,9155 |
таблица 11
На основе данных построим график, график изображен на рисунке 14:
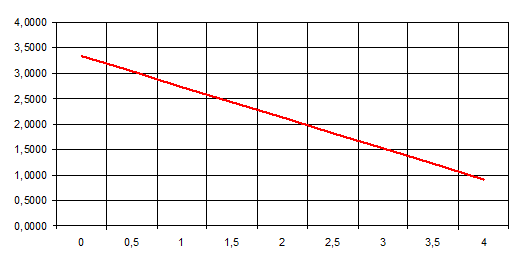
рис. 14 График распределения тока вдоль вертикальной части антенны
2.5.7.4. Распределение напряжения вдоль вертикальной части антенны:
Распределение напряжения вдоль вертикальной части антенны задаётся косинусоидальным законом с пучностью на изолированном конце горизонтальной части антенны:
Результаты расчётов представлены в таблице 12:
| zv (м) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| Uv (В) | 15663,74 | 15668,29 | 15672,4 | 15676,09 | 15679,34 | 15682,16 | 15684,55 | 15686,5 | 15688,03 |
таблица 12
Зависимость распределения напряжения показана на рисунке 15:
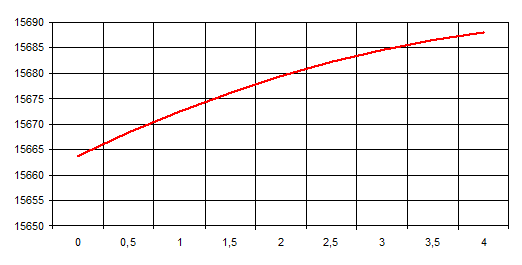
рис. 15 График распределения напряжения вдоль вертикальной части антенны
Напряжение в антенне сильно зависит от тока и ёмкости антенны, при больших мощностях, ток в антенне сильно возрастает, особенно на длинных волнах, когда сопротивление антенны мало, тогда сильно возрастает напряжение в антенне, что недопустимо с точки зрения электрической прочности. Максимально допустимое напряжение ограничивается возможностью изоляции, а также возникновением явления коны (ионизации воздуха, возникающая при перенапряжениях в антенне).
Для уменьшения напряжения в антенне на фиксированной частоте, следует увеличивать статическую ёмкость, путём увеличения числа проводов в горизонтальной и вертикальной частях.
2.5.7.5. Распределение тока вдоль горизонтальной части:
Определяется выражением:
zg - меняется от 0 до 7 метров - конца горизонтальной части антенны;
Ipg - ток в пучности.
Расчёты представим в виде таблицы 13:
| zg (м) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ig (А) | 0,9155 | 0,784902 | 0,654217 | 0,52346 | 0,392646 | 0,261788 | 0,130901 | 0 |
таблица13
Зависимость распределения тока вдоль горизонтальной части антенны изображена на рисунке 16:
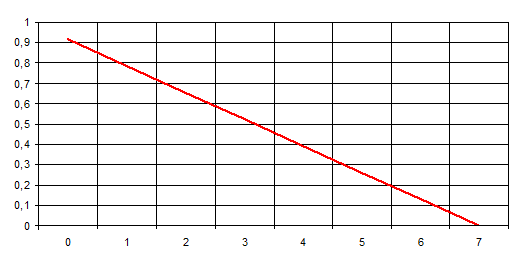
рис. 16 График распределения тока вдоль горизонтальной части антенны
2.5.7.6. Распределение напряжения вдоль горизонтальной части:
Определяется выражением:
Распределение напряжении вдоль горизонтальной рассчитано в таблице 14 :
| zg (м) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ug (В) | 15647,64 | 15658,87 | 15668,38 | 15676,16 | 15682,22 | 15686,54 | 15689,14 | 15690 |
таблица 14
Зависимость распределения напряжения вдоль горизонтальной части антенны представлена на рисунке 17:
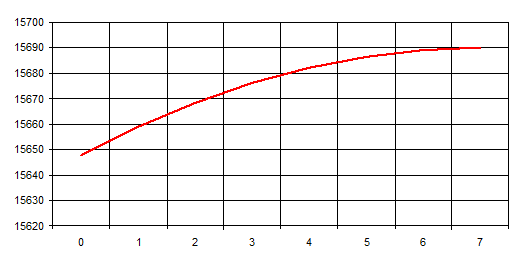
рис. 17 График распределения напряжения вдоль горизонтальной части антенны
3.1. Список используемой литературы:
1). Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства.- М.: Советское радио, 1974.
2). Кочержевский Г.Н. Антенно-фидерные устройства.- М: Радио и связь, 1981.
3). Вершков М.В. Судовые антенны.- Л: Судостроение, 1979.