| Скачать .docx |
Курсовая работа: Анализ избирательных цепей в частотной и временной областях
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Харьковский национальный университет радиоэлектроники
Кафедра основ радиотехники
Курсовая работа по дисциплине
"ОСНОВЫ РАДИОЭЛЕКТРОНИКИ"
на тему
“АНАЛИЗ ИЗБИРАТЕЛЬНЫХ ЦЕПЕЙ В ЧАСТОТНОЙ И ВРЕМЕННОЙ ОБЛАСТЯХ”
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Выполнил:
студент группы
Консультант
ХАРЬКОВ 2009
Реферат
Курсовая работа: 19 с., 12 рис., 10 табл., 5 источников.
Объект исследования - пассивная линейная цепь второго порядка.
Цель работы - определить отклик пассивной линейной цепи, к входу которой приложен входной сигнал.
Метод исследования - отклик цепи следует определить спектральным и временным методами.
Расчет отклика в пассивной цепи находится двумя способами. Для расчета отклика спектральным способом входной сигнала разлаживается на гармоники, строятся АЧС и ФЧС и, рассчитав комплексный коэффициент передачи, находится выходные спектры, из которых синтезируется выходной сигнал. Для расчета отклика временным методом рассчитываются временные характеристики на периодическую последовательность прямоугольных импульсов.
ИЗБИРАТЕЛЬНАЯ ЦЕПЬ, ОТКЛИК, АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, АЧС, ФЧС, ФИЛЬТР, АЧХ, ФЧХ, ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА, ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА
Содержание
1. Расчёт спектра входного сигнала.
2. Расчет частотных характеристик
2.1 Расчет амплитудно-частотной характеристики цепи
2.2 Расчет фазо-частотной характеристики цепи
4. Расчет временных характеристик
5. Расчет отклика с помощью переходной характеристики
Задание к курсовому проекту
Параметры обобщенной схемы представлены в таблице 1 (R - указано в омах, L - в микрогенри, C - в нанофарадах, T - в миллисекундах, ![]() - микросекундах).
- микросекундах).
Таблица 1 - Параметры обобщенной схемы
| Воздействие |
Отклик |
|
|
|
|
|
||||||||||
| R |
L |
C |
R |
L |
C |
R |
L |
C |
R |
L |
C |
R |
L |
C |
||
|
|
|
140 |
0 |
∞ |
0 |
150 |
∞ |
60 |
0 |
∞ |
0 |
0 |
∞ |
0 |
0 |
0 |
Изобразим в соответствии с обобщенной схемой схему исследуемого варианта.

Рисунок 1 - Анализируемая схема
Введение
Дисциплина "Основы радиоэлектроники" принадлежит к фундаментальным дисциплинам в образовании специалистов, которые проектируют электронную аппаратуру. Курсовая работа по этой дисциплине - один из этапов самостоятельной работы, который позволяет определить и исследовать частотные и временные характеристики избирательных цепей, установить связь между предельными значениями этих характеристик, а также закрепить знания по спектральному и временному методам расчета отклика цепи.
1. Расчёт спектра входного сигнала.
Используя таблицу 1, представим параметры входного сигнала U1 (t) табл.1.1
Таблица 1.1 - Параметры воздействия
| A |
|
|
|
| 5 |
19 |
10 |
0.19 |
Значение А - в вольтах, т.к входной сигнал - напряжение. Изобразим соответственно с обобщенной часовой диаграммой и данных табл.1.1 график U1 (t).

Рисунок 1.1 - Временная диаграмма входного сигнала
Определим амплитуды гармоник входного сигнала. Для прямоугольного импульса формула будет иметь вид:
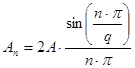 , где
, где ![]() - скважность.
- скважность.
Спектр фаз входного сигнала:![]() , где
, где ![]() - время задержки.
- время задержки.
Полученные амплитуды и фазы гармоник занесем в табл.1.2 и построим спектральные диаграммы входного сигнала (рис.1.2).
Таблица 1.2 - Расчет спектра входного сигнала
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0.5 |
0.98 |
0.94 |
0.86 |
0.76 |
0.64 |
0.51 |
0.37 |
0.234 |
0.11 |
0 |
|
|
- |
-0.33 |
-0.66 |
-0.99 |
-1.32 |
-1.65 |
-1.98 |
-2.32 |
-2.65 |
-2.98 |
- |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
0.09 |
0.16 |
0.2 |
0.22 |
0.21 |
0.19 |
0.15 |
0.1 |
0.052 |
0 |
|
|
|
-6.78 |
-7.11 |
-7.44 |
-7.77 |
-8.1 |
-8.43 |
-8.76 |
-9.09 |
-9.425 |
- |

а)

б)
Рисунок 1.2 - Спектральная диаграмма входного сигнала
2. Расчет частотных характеристик
Рассчитаем комплексную передаточную функцию схемы (рис.1):
 .
.
Для определения ![]() предположим, что напряжение
предположим, что напряжение ![]() известен и по закону Ома в комплексной форме определим
известен и по закону Ома в комплексной форме определим ![]() :
:
![]()
![]()
![]()
![]()
Рассчитаем полиномиальные коэффициенты:
![]()
![]()
![]()
![]()
![]()
![]()
2.1 Расчет амплитудно-частотной характеристики цепи
 .
.
АЧХ рассчитываем на частотах ![]()
![]() , кратных частоте прохождения периодического несинусоидального входного сигнала
, кратных частоте прохождения периодического несинусоидального входного сигнала ![]() , отклик для которого нужно определить.
, отклик для которого нужно определить.
Результаты расчета АЧХ заносим в табл.2.1 и табл.2.2:
Таблица 2.1 - Результаты расчетов АЧХ
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
7.14 |
7.12 |
7.05 |
6.94 |
6.8 |
6.66 |
6.51 |
6.36 |
6.23 |
6.1 |
6 |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
5.9 |
5.8 |
5.72 |
5.65 |
5.59 |
5.54 |
5.49 |
5.45 |
5.41 |
5.38 |
По данным расчетов строим график АЧХ (рис.2.1а).
2.2 Расчет фазо-частотной характеристики цепи
![]() ,
,
где ![]() - аргумент числителя
- аргумент числителя ![]() ;
; ![]() - аргумент знаменателя
- аргумент знаменателя ![]()
![]()
![]()
Расчет ФЧХ выполняется для тех же частот, что и АЧХ. Результаты расчета АЧХ заносим в табл.2.3 и табл.2.4:
Таблица 2.3 - Результаты расчета ФЧХ
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
-0.04 |
-0.07 |
-0.1 |
-0.12 |
-0.14 |
-0.16 |
-0.17 |
-0.173 |
-0.176 |
-0.177 |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
-0.18 |
-0.175 |
-0.172 |
-0.17 |
-0.165 |
-0.16 |
-0.156 |
-0.15 |
-0.148 |
-0.143 |
По данным расчетов строим график АЧХ (рис.2.1б).

а)
 б)
б)
Рисунок 2.1 - Частотные характеристики
3. Расчет спектра отклика
Поскольку амплитуды гармонических, составляющих отклика определяется как ![]() , а начальные фазы
, а начальные фазы ![]() , результаты расчетов представим в табл.3.1, в которую сведем ранее рассчитанные значения для одинаковых частот.
, результаты расчетов представим в табл.3.1, в которую сведем ранее рассчитанные значения для одинаковых частот.
Таблица 3.1 - Расчет спектра отклика
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0.5 |
0.98 |
0.94 |
0.86 |
0.76 |
0.64 |
0.51 |
0.37 |
0.234 |
0.11 |
0 |
|
|
7.14 |
7.12 |
7.05 |
6.94 |
6.8 |
6.66 |
6.51 |
6.36 |
6.23 |
6.1 |
6 |
|
|
3.57 |
7 |
6.6 |
6 |
5.1 |
4.24 |
3.3 |
2.34 |
1.46 |
0.67 |
0 |
|
|
- |
-0.33 |
-0.66 |
-0.99 |
-1.32 |
-1.65 |
-1.98 |
-2.32 |
-2.65 |
-2.98 |
- |
|
|
0 |
-0.04 |
-0.07 |
-0.1 |
-0.12 |
-0.14 |
-0.16 |
-0.17 |
-0.173 |
-0.176 |
-0.177 |
|
|
- |
-0.37 |
-0.73 |
-1.09 |
-1.45 |
-1.8 |
-2.14 |
-2.48 |
-2.82 |
-3.15 |
- |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
0.09 |
0.16 |
0.2 |
0.22 |
0.21 |
0.19 |
0.15 |
0.1 |
0.052 |
0 |
|
|
|
5.9 |
5.8 |
5.72 |
5.65 |
5.59 |
5.54 |
5.49 |
5.45 |
5.41 |
5.38 |
|
|
|
0.53 |
0.9 |
1.13 |
1.22 |
1.19 |
1.05 |
0.83 |
0.57 |
0.28 |
0 |
|
|
|
-6.78 |
-7.11 |
-7.44 |
-7.77 |
-8.1 |
-8.43 |
-8.76 |
-9.09 |
-9.425 |
- |
|
|
|
-0.18 |
-0.175 |
-0.172 |
-0.17 |
-0.165 |
-0.16 |
-0.156 |
-0.15 |
-0.148 |
-0.143 |
|
|
|
-6.96 |
-7.29 |
-7.61 |
-7.94 |
-8.27 |
-8.59 |
-8.92 |
-9.25 |
-9.57 |
- |
По данным расчетам изобразим спектральные диаграммы амплитуд и фаз отклика (рис.3.1).

а)

б)
Рисунок 3.1 - Спектральная диаграмма выходного сигнала
Временная функция отклика в виде n гармоник имеет вид:

Для мгновенных значений тока для ![]() представлены в таблице 3.3
представлены в таблице 3.3
Таблица 3.3 - Расчет отклика
| t, мкс |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
| I1 , мА |
10.14 |
22.896 |
33.061 |
36.345 |
34.277 |
32.42 |
34.436 |
38.169 |
37.889 |
30.293 |
17.963 |
6.958 |
1.415 |
0.734 |
1.503 |
1.294 |
По результатам расчетов построим график отклика, найденный спектральным методом для n гармоник (n=20) (рис.3.2).

Рисунок 3.2 - Временная диаграмма отклика
4. Расчет временных характеристик
Перепишем полином знаменателя ![]()
![]() , в котором заменим
, в котором заменим ![]() , приравняв его к нулю; получим характеристическое уравнение:
, приравняв его к нулю; получим характеристическое уравнение:
![]() ,
,
решим его для ранее найденных полиноминальных коэффициентов:
![]() ;
;
![]() .
.
Свободная составляющая переходной характеристики:
![]() ,
,
где ![]() - постоянная интегрирования.
- постоянная интегрирования.
Принужденная составляющая тока соответствует постоянному току в цепи с условием, что индуктивность эквивалентна короткому замыканию, емкость разрыву, а ![]() .
.
![]() .
.
Переходная характеристика:
![]() .
.
Для нахождения постоянной интегрирования ![]() , определим по схеме
, определим по схеме ![]() (см. рис.1.1). Запишем уравнения по законам Кирхгофа для
(см. рис.1.1). Запишем уравнения по законам Кирхгофа для ![]() :
:

Т. к. временные характеристики определяются при нулевых начальных условиях ![]() ,
, ![]() , из первого уравнения системы можно записать:
, из первого уравнения системы можно записать:
![]()
Исходя из этого, второе уравнение системы примет вид:
![]() .
.
Значение напряжения найдено при условии, что ![]() , т.е. это значение отвечает начальным значениям переходной характеристики:
, т.е. это значение отвечает начальным значениям переходной характеристики:
![]() .
.
Найдем
![]() ,
, ![]() ,
, ![]()
![]() .
.
Тогда переходная характеристика примет вид:
![]() .
.
![]() ,
, ![]()
Импульсную характеристику ![]() найдем из переходной как:
найдем из переходной как:
![]() ,
,
![]() ,
, ![]()
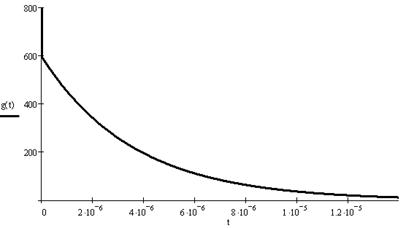
По полученным выражениям рассчитаем временные характеристики.
Таблица 4.1 Таблица 4.2
Расчет переходной характеристики Расчет импульсной характеристики
|
|
|
|
|
|
|
|
|
|
| 0 |
5 |
10 |
7.013 |
0 |
|
10 |
36.486 |
|
| 1 |
5.523 |
11 |
7.044 |
1 |
453.47 |
11 |
27.576 |
|
| 2 |
5.919 |
12 |
7.068 |
2 |
342.725 |
12 |
20.841 |
|
| 3 |
6.218 |
13 |
7.087 |
3 |
259.026 |
13 |
15.751 |
|
| 4 |
6.444 |
14 |
7.1 |
4 |
195.768 |
14 |
11.905 |
|
| 5 |
6.614 |
15 |
7.111 |
5 |
147.958 |
15 |
8.997 |
|
| 6 |
6.743 |
16 |
7.119 |
6 |
111.824 |
16 |
6.8 |
|
| 7 |
6.841 |
17 |
7.125 |
7 |
84.515 |
17 |
5.139 |
|
| 8 |
6.915 |
18 |
7.129 |
8 |
63.875 |
18 |
3.884 |
|
| 9 |
6.97 |
19 |
7.132 |
9 |
48.276 |
19 |
2.936 |
По полученным данным строим графики временных характеристик (рис.4.1).

а)
б)
Рисунок 4.1 - Временные характеристики
5. Расчет отклика с помощью переходной характеристики
Поскольку за время, равное периоду T воздействия, временные характеристики практически достигают значения принужденной составляющей, отклик на периодическое воздействие можно найти как повторяющийся отклик на воздействие в виде одиночного прямоугольного импульса:

Таблица 5.1 - Расчет отклика цепи временным методом
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
|
|
25 |
29.6 |
32.2 |
33.7 |
34.6 |
35.1 |
35.3 |
35.5 |
35.6 |
35.65 |
8.1 |
4.6 |
График отклика представлен на рис.5.1.

Рисунок 5.1 - Временная диаграмма отклика
Выводы
В ходе работы над курсовым проектом анализировалась схема цепи второго порядка в частотной и временной областях.
В результате выполнения работы усвоили спектральный и временной методы анализа цепей. Также было установлено влияние изменения элементов схемы на частотные и временные характеристики цепи. Связь между временными и частотными характеристиками установлена.
Были построены амплитудно-частотный и фазо-частотный спектры периодического прямоугольного входного сигнала.
Временные диаграммы отклика, найденные временным и частотным методами в значительной мере совпадают. Это свидетельствует о правильности расчетов.
Список литературы
1. Попов В.П. Основы теории цепей: Учебник для вузов. M.: Высш. шк., 1985. -490 с.
2.3ернов Н.В., Карпов В.Г. Теория радиотехнических цепей. - М.: Энергия, 1972. - 715с.
З. Афанасьев В.П. и др. Теория линейных электрических цепей: Учебное пособие для вузов. - М.: Высш. шк., 1973. - 592 с.
4. Белецкий А.Ф. Теория линейных электрических цепей: Учебник для вузов. - М.: Радио и связь, 1986. - 544 с.
5. Методичні вказівки до курсової роботи з дисципліни „Основи радіоелектроніки”. - Харків: ХНУРЕ, 2003.