| Скачать .docx |
Курсовая работа: Помехоустойчивость систем связи
Оглавление.
1. Введение.
2. Задание на курсовую работу.
3. Исходные данные.
4. Структурная схема системы связи.
5. Временные и спектральные диаграммы на выходах функциональных блоков системы связи.
6. Структурная схема приемника.
7. Принятие решения по одному отсчету.
8. Вероятность ошибки на выходе приемника.
9. Выигрыш в отношении сигнал/шум при применении оптимального приемника.
10. Максимально возможная помехоустойчивость при заданном виде сигнала.
11. Принятие решения приемником по трем независимым отсчетам.
12. Вероятность ошибки при использовании метода синхронного накопления.
13. Расчет шума квантования при передаче сигналов методом ИКН.
14. Использование сложных сигналов и согласованного фильтра.
15. Импульсная характеристика согласованного фильтра.
16. Схема согласованного фильтра для приема сложных сигналов. Форма сложных сигналов на выходе СФ при передаче символов “1” и “0”.
17. Оптимальные пороги решающего устройства при синхронном и асинхронном способах принятия решения при приеме сложных сигналов согласованным фильтром.
18. Энергетический выигрыш при применении согласованного фильтра.
19. Вероятность ошибки на выходе приемника при применении сложных сигнал согласованного фильтра.
20. Пропускная способность разработанной системы связи.
21. Заключение.
Введение.
Задачей данной курсовой работы является описание системы связи для передач непрерывного сообщения дискретными сигналами.
Передача информации занимает высокое место в жизнедеятельности современного общества. Самая главная задача, при передаче информации – это передача её без искажений. Наиболее перспективным в этом направлении является передача аналоговых сообщений дискретными сигналами. Этот метод дает большое преимущество в помехоустойчивости линий информации. Все современные информационные сети строятся на этом принципе.
Кроме этого дискретный канал связи прост в эксплуатации и, по нему можно передавать любую информацию, т.е. он обладает универсальностью. Все это делает такие каналы связи наиболее перспективными в данный момент.
1. Задание на курсовую работу.
Разработать обобщенную структурную схему системы связи для передачи непрерывных сообщений дискретными сигналами, разработать структурную схему приемника и структурную схему оптимального фильтра, рассчитать основные характеристики разработанной системы связи и сделать обобщающие выводы по результатам работы.
2. Исходные данные.
1) Номер варианта N=1.
2) Вид сигнала в канале связи DAM .
3) Скорость передачи сигналов V=6000 Бод.
4) Амплитуда канальных сигналов А=3 мВ.
5) Дисперсия шума x*x=0.972 мкВт.
6) Априорная вероятность передачи символов “1” p(1)=0.09.
7) Способ передачи сигнала КГ .
8) Полоса пропускания реального приемника Df=12 кГц.
9) Значение отсчёта Z(t0)=0.75 мВ
d f=12 кГц.
10) Значение отсчётов Z(t1)=0.75мВ
Z(t2)=0.45мВ
Z(t3)=0.83мВ.
11) Максимальная амплитуда на выходе АЦП b max=2.3 В.
12) Пик фактор П.=1,6.
13) Число разрядов двоичного кода n=8.
14) Вид дискретной последовательности сложного сигнала
1 -1 1 -1 -1 -1 1 1 -1
3. Структурная схема системы связи.
Система связи представляет собой совокупность радиотехнических средств, обеспечивающих передачу информации от источника к получателю. Рассмотрим схему системы связи.

Устройство, преобразующее сообщение в сигнал, называют передающим устройством, а устройство, преобразующее принятый сигнал в сообщение, приемным устройством.
Рассмотрим передающее устройство:
Фильтр нижних частот ограничивает спектр исходного сообщения, чтобы он удовлетворял теореме Котельникова, что необходимо для дальнейшего преобразования.
Аналогово-цифровой преобразователь (АЦП) преобразует непрерывное сообщение в цифровую форму. Это преобразование состоит из трех операций: сначала непрерывное сообщение подвергается дискретизации по времени через интервал; полученные отсчеты мгновенных значений квантуются (Квант.); полученная последовательность квантованных значений передаваемого сообщения представляется в виде последовательности двоичных кодовых комбинаций посредством кодирования.
Полученный выхода АЦП сигнал поступает на вход Амплитудного модулятора, где последовательность двоичных импульсов преобразуется в радиоимпульсы, которые поступают непосредственно в канал связи.
На приемной стороне канала связи последовательность импульсов после демодуляции в демодуляторе поступает на вход цифро-аналогового преобразователя (ЦАП), назначение которого состоит в восстановлении непрерывного сообщения по принятой последовательности кодовых комбинаций. В состав ЦАП входит Декодер, предназначенный для преобразования кодовых комбинаций в квантовую последовательность отсчетов, и сглаживающий фильтр (ФНЧ), восстанавливающий непрерывное сообщение по квантованным значениям.
4. Временные и спектральные диаграммы на выходах функциональных блоков системы связи.
1) Непрерывное сообщение.

2) Фильтр низких частот.

3) Дискретизатор.

4) Квантователь.

5) Кодер.

6) Модулятор.

7) Канал связи.

8) Демодулятор.

9) Декодер.

10) Фильтр нижних частот.

11) Получатель.

5. Структурная схема приёмника.

При когерентном приеме применяется синхронный детектор, который устраняет влияние ортогональной составляющей вектора помехи. Составляющая x=E
п
·
cosj имеет нормальный закон распределения и мощность ![]() .
Поэтому вероятность искажения посылки р
(0/1) и вероятность искажения паузы р
(1/0) будут равны
.
Поэтому вероятность искажения посылки р
(0/1) и вероятность искажения паузы р
(1/0) будут равны
Сигнал Z(t) поступает на перемножитель, где происходит его перемножение с сигналом, пришедшим с линии задержки. Далее сигнал подвергается интегрированию, после чего он поступает на решающее устройство, где выносится решение в пользу сигнала S1(t) или S2(t).
6. Принятие решения по одному отсчёту.
Сообщения передаются последовательностью двоичных символов «1» и «0», которые появляются с априорными вероятностями соответственно P(1)=0.09 и P(0)=0.91.
Этим символам соответствуют начальные сигналы S1 и S2,которые точно известны в месте приема. В канале связи на передаваемые сигналы воздействует Гауссовский шум с дисперсией D=0.972 мкВт. Приёмник, оптимальный по критерию идеального наблюдателя принимает решения по одному отсчету смеси сигнала и помехи на интервале сигнала длительностью Т .
Для принятия «1» по критерию идеального наблюдателя необходимо выполнение неравенства:
в противном случае принимается «0».
Для применения критерия идеального наблюдателя необходимо выполнение трех условий:
Чтобы сигналы были полностью известны.
1) Чтобы в канале связи действовали помехи с Гауссовским законом распределения.
2) Чтобы были известны априорные вероятности сигналов.
 |
 |
Плотности вероятностей найдём по формулам:
 |
Для вычисления плотности распределения помехи применим формулу:
Так как
(0.096<10.1), то на выходе решающего устройства будет зарегистрирован “0”.
Рассчитаем таблицы и построим графики для:
x |
0 | ±s | ±2s | ±3s | |
| W(x) | 406 | 247 | 150 | 91.5 |
| Z | 0 | -Z | +Z | -2Z | +2Z | -3Z | +3Z | +a |
| W(Z/0) | 406 | 304 | 304 | 127 | 127 | 30 | 30 | 4 |
| W(Z/1) | 4 | 0.3 | 30 | 0.012 | 127 | 0.0003 | 304 | 406 |

График плотностей распределения W(Z/1) и W(Z/0).

График плотности распределения помехи.
7. Вероятность ошибки на выходе приемника.
Рассчитаем вероятность неправильного приема двоичного символа в рассматриваемом приемнике
Для сигналов вида ДАМ КГ приема вероятность ошибки вычисляется следующим образом:
Рош.= ,
,
где ![]() – отношение сигнал / шум,
– отношение сигнал / шум,
а Ф(z
) -интеграл вероятностей(табулированный).
-интеграл вероятностей(табулированный).
Полоса пропускания реального приемника, определяется шириной спектра двоичных сигналов и равна:
Df=2/T=2/0.00016=12 кГц
 |
Вычислим отношение сигнал/шум:
Вычислим Рош:
Рош.=
Построим график P(h) и укажем на нем точку h=2.152 соответствующую Рош=0,064:

8. Выигрыш в отношении сигнал/шум при применении оптимального приемника.
В предположении оптимального приема (фильтрации) сигналов определим:
a)
 |
Максимально возможное отношение сигнал/шум.
 |
где Ес-энергия принимаемых посылок;
 |
Т-длительность элемента сигнала; А-амплитуда сигнала; No-спектральная плотность помехи.
 |
Тогда:
b)
 |
Выигрыш в отношении сигнал/шум оптимального приемника по сравнению с рассчитанным получается:
9. Максимально возможная помехоустойчивость при заданном виде сигнала.
 |
Для определения потенциальной помехоустойчивости приема символов определим среднюю вероятность ошибки при оптимальном приеме для заданного вида сигнала (ДАМ):
Котельников В.А. определил потенциальную помехоустойчивость как максимально возможную помехоустойчивость при заданном характере помех. Максимальная помехоустойчивость достигается при оптимальной фильтрации сигналов, т.е. при максимальном отношении сигнал/шум и, соответственно, при минимальной Рош. Эта помехоустойчивость называется потенциальной, т.к. она не может быть превзойдена никаким другим приемником. Для любого реального приемника помехоустойчивость может быть определена расчетным или экспериментальным путем. Ее сравнение с потенциальной помехоустойчивостью позволяет установить, сколь совершенен данный приемник и целесообразно ли его улучшение.
10. Принятие решения приемником по трем независимым отсчетам.
Определим какой символ будет зарегистрирован на приеме при условии, что решение о переданном символе принимается по совокупности трех некоррелированных(независимых) отсчетов Z1=0.75 мВ; Z2=0.45 мВ; Z3=0.83 мВ.
 |
 |
Для вычисления отношения правдоподобия найдем совместную плотность распределения трех отсчетов для каждого из сигналов. С учетом некоррелированности:
 |
Сравним полученное l с пороговым lо, т.к. l<<lо, то приемник примет решение в пользу “0”.
11. Вероятность ошибки при использовании метода синхронного накопления.
Для повышения помехоустойчивости приема дискретных двоичных сообщений решения о переданном символе принимается не по одному отсчету на длительности элемента сигнала 0£t£T, а по нескольким, в нашем случае по трем некоррелированным отсчетам Z1(t),Z2(t),Z3(t) принимаемой смеси сигнала и помехи(метод дискретного накопления). При этом отсчеты берутся через интервал Dt, равный интервалу корреляции помехи tоx, т.е. они будут некоррелированными.
Прием методом многократных отсчетов позволяет по сравнению с принятием решения по одному отсчету увеличить позволяет увеличить отношение сигнал/шум в данном случае в три раза. Это обусловлено тем, что мощность сигнала возрастает в nІ(3і), а мощность помехи- только в n(3) раза.
Так как сигнал – величина детерминированная, то его составляющие складываются по напряжению, а составляющие помехи, как величины случайной, складываются по мощности. Характерно, что при приеме дискретных сигналов методом многократных отсчетов можно получить сколь угодно значительное отношение сигнал/шум (и, соответственно, высокую помехоустойчивость) путем увеличения числа отсчетов на длительности элемента сигнала. Однако очевидно, что это требует увеличения длительности элемента сигнала тоже в n раз, что в свою очередь, приводит к снижению скорости передачи сообщений также в n раз по сравнению с вариантом принятия решения по одному отсчету. Таким образом, реализуется принцип обмена скорости передачи дискретных сообщений на помехоустойчивость путем увеличения энергии элемента сигнала.
 |
Найдем ожидаемую среднюю вероятность ошибки в приемнике, использующем метод синхронного накопления
12. Расчет шума квантования при передаче сигналов методом ИКН.
В системе ИКМ сигнал представляет собой последовательность кодовых комбинаций, отображающих квантованные по уровню значения передаваемого сообщения b(t):

Каждая кодовая комбинация содержит к элементарных посылок одинаковой длительности. В общем случае эти посылки могут принимать m значений. Это позволяет кодировать и передавать
Для передачи посылок кодовых комбинаций может быть использован любой из способов передачи дискретных сообщений.
Особенностью ИКМ является то, что даже при полном отсутствии помех в канале, принятое сообщение отличается от передаваемого, поскольку квантованное сообщение лишь приблизительно совпадает с исходным. Поэтому при отсутствии помех переданное сообщение состоит из суммы переданного сообщения плюс шум квантования. Шум квантования обусловлен тем, что преобразование непрерывных сообщений в цифровую форму в системах ИКМ сопровождается округлением мгновенных значений до ближайших разрешенных уровней квантования.
 |
 |
Рассчитаем мощность шума квантования и отношение сигнал/шум квантования hІкв для случая поступления на вход приемника сигнала с максимальной амплитудой bmax=2.3 В.
 |
 |
Рс - энергия сигнала, П-пик фактор входного сигнала (П.=1.6), Рш. кв-энергия шумов квантования, n=8-число разрядов второго кода.
13. Использование сложных сигналов и согласованного фильтра.
Решение проблемы повышения помехозащищенности систем связи и управления достигается использованием различных методов и средств, в том числе и сигнал сложной формы (с большой базой).
Широкое практическое применение получили сложные сигналы на основе дискретных кодовых последовательностей, которые представляют собой последовательности символов diдлительностью Т, принимающих одно из двух значений:+1 или –1. Такие сигналы легко формируются и обрабатываются с использованием элементов цифровой и вычислительной техники.
Сложные сигналы должны удовлетворять ряду требований для достижения наибольшей достоверности их приема:
1) корреляционная функция должна содержать значительный максимум (пик);
2)
 |
взаимная корреляционная функция (ВКФ):
любой пары сигналов из используемого ансамбля, определяющая степень их ортогональности, должна быть близка к нулю при любом t.
Однако на практике для реальных сигналов последнее условие не может быть выполнено. Поэтому для используемых сигналов важно обеспечить, возможно, большее отношение Kii(t)/Kij(t), оно и будет определять помехозащищенность приема сигналов (для случая передачи двоичных сообщений это будут вероятности Р.(1/0) и Р.(0/1)). Отличительная особенность ВФК в том. Что она не является четной функцией аргумента t, т.е. Kuv(t)¹Kuv(-t), а максимальный выброс достигается не обязательно при t=0.
Изобразим форму заданных сигналов при передаче по каналу связи символов “1” и “0” в предположении, что S2(t)=-S1(t), при этом длительность каждого из сигналов равна n*T, где n=9 – число элементов сложного сигнала:
S1(t)={1;0;1;0;0;0;1;1;0} = {1;-1;1;-1;-1;-1;1;1;-1}
S2(t)=- S1(t)={-1;1;-1;1;1;1;-1;-1;1}

14. Импульсная характеристика согласованного фильтра.
 |
Сигнал на выходе согласованного фильтра в произвольный момент времени характеризуется интегралом свертки вида:
где g(t) – импульсная характеристика фильтра. Импульсная характеристика (ИХ) – это отклик фильтра (цепи) на дельта функцию d(t), т.е. g(t)=Ф.(d(t)).
ИХ связанна с АЧХ фильтра парой преобразований Фурье (ППФ):
 |
Решая данный интеграл с учетом to=Tc (длительность сигнала) получим:
т.е. ИХ согласованного фильтра (СФ) представляет собой с точностью до постоянной, а зеркальное отображение временной функции входного сигнала, сдвинутое вправо по оси tна to=Tc.
Изобразим ИХ для сигнала S1(t):

15. Схема согласованного фильтра для приема сложных сигналов. Форма сложных сигналов на выходе СФ при передаче символов “1” и “0”.
Согласованный фильтр для дискретных последовательностей может быть реализован в виделинии задержки с отводами (с общим временем задержки, равным длительности сигнала Tc), фазовращателей (инверторов) в отводах и суммирующей схемы, на выходе которой возникает импульс, равный сумме амплитуд всех элементов сигнала.

Импульсы последовательности S1(t) поступают на линию задержки, имеющую отводы через каждые t интервалы, далее на фазовращающие каскады и схему суммирования.
Фазосхраняющие и фазоинвертирующие каскады включены в порядке, соответствующем чередованию биполярных импульсов последовательности.
При приеме последовательность продвигается по линии задержки, в момент, когда все импульсы последовательности совпадут по знаку с каскадами, включенными между отводами линии задержки и суммирующим устройством, тогда все импульсы складываются и на выходе появляется наибольший импульс; при всех других сдвигах суммирование производится не в фазе (с разными знаками).
Рассчитаем форму помехи в предположении. Что на вход фильтра поступает непрерывная последовательность знакопеременных символов {-1;1;-1;1;-1;1;-1;1;-1}.
Помеха x(t).
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y(nT) | -1 | 2 | 1 | 0 | 3 | 0 | -1 | -2 | 1 | 0 |
Рассчитаем форму полезного сигнала на выходе фильтра при передаче символа”1”. При передаче символа “1” сигнал на выходе СФ представляет собой функцию корреляции сложного сигнала, сдвинутого на время задержки.
 |
Функция корреляции вычисляется по формуле:
Полезный сигнал S1(t).
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| nT | 9 | -2 | -1 | -2 | 1 | 0 | -1 | 2 | -1 | 0 |
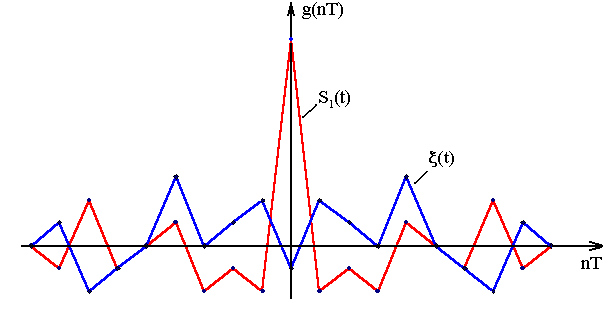
16. Оптимальные пороги решающего устройства при синхронном и асинхронном способах принятия решения при приеме сложных сигналов согласованным фильтром.
Изобразим графики выходных сигналов на выходе СФ при передаче символов “1” и “0”.

Регистрация в решающем устройстве происходит в момент времени t=T. Рассмотрим структурные схемы для приема сообщений синхронным и асинхронным способами принятия решения в решающей схеме по выходному сигналу СФ.
Асинхронный метод.

При асинхронном способе приема, сигнал формируется на выходе СФ и поступает на РУ. В РУ сигнал сравнивается с пороговым и в соответствии с результатом выдается либо “0”, либо “1”. Порог при таком способе вычисляется как среднее между максимумом функции корреляции и следующим после максимума пиковым значением:
Синхронный метод.

При синхронном способе приема Uп=0, за счет синхронизации сигнал в решающей схеме сравнивается с Uп=0 в момент времени to=Tc, когда функция корреляции имеет значение максимума.
Для обеспечения большой ПУ целесообразно выбрать синхронный способ приема сигнала, но с точки зрения реализации схемы трудно обеспечить условие синхронизации. На практике ставится вопрос об обеспечении высокой ПУ либо простой схемы приемника.
17. Энергетический выигрыш при применении согласованного фильтра.
СФ обеспечивает при флуктуационной помехе в канале типа «белого шума» в момент окончания сигнала to=Tcна своем выходе максимально возможное отношении пиковой мощности сигнала к мощности помехи. Выигрыш в отношении сигнал/шум на выходе СФ по сравнению со входом равняется базе сигнала, при прохождении через интегратор изменяется только помеха
 |
Энергетический выигрыш:
Где Т – длительность сигнала;Dtо – длительность элемента сигнала.
Таким образом, выиграли g=9, обеспечиваемый СФ при приеме дискретных последовательностей, составляет 9 раз (в общем случае N-число элементов в дискретной последовательности). Следовательно, путем увеличения длинны дискретных последовательностей, отображающих символы сообщений “1” и “0”, можно обеспечить значительное повышение отношения сигнал/шум на входе решающей схемы приемника и, соответственно, повышение помехоустойчивости передачи дискретных сообщений. Это будет приводить к снижению скорости передачи сообщений, т.е. реализуется принцип обмена скорости передачи дискретных сообщений на ПУ их приема путем увеличения энергии сигнала.
18. Вероятность ошибки на выходе приемника при применении сложных сигналов и согласованного фильтра.
При определении вероятности ошибки считаем, что сигналы соответствующие символам “1” и “0”, являются взаимнопротивоположными и решение о переданном символе принимается с использованием пороговой решающей схемы синхронным способом.
 |
При указанных условиях отношение сигнал/шум на выходе СФ в g=9 раз больше,чем на выходе
19. Пропускная способность разработанной системы связи.
Скорость передачи информации, при отсутствии помех в системах связи, численно равна производительности источника сообщений. При наличии помех учитывается только взаимная информация.
Пропускная способность (ПС) канала связи - максимально возможная скорость передачи информации по каналу
 |
Вычислим ПС непрерывного канала связи для заданных Dfпр и hІ:
Вычислим энтропию двоичного источника сообщений, передаваемых по дискретному каналу связи с априорными вероятностями Р(1)=0.09 и Р.(0)=0.91, и производительностью этого источника:

Определим избыточность:
Избыточность составляет 86.9 %, наличие избыточности приводит к загрузке канала связи передачей букв сообщений, которые не несут информации (их можно убрать и не передавая).
20. Заключение.
Выполним сравнительный анализ ПУ рассмотренной системы связи для различных способов приема дискретных сигналов.
| Метод приема | Рош.ср. |
| Метод однократного отсчета | 6,4*10ˉІ |
| Метод однократного отсчета при оптимальном приеме | 8,2*10ˉі |
| Метод синхронного накопления (по трем отсчетам) | 4,6*10ˉі |
| С помощью СФ, сигналов с большой базой | <10ˉ№І |
Из приведенной таблицы можно сделать вывод, что самым не помехоустойчивым методом приема сигналов является метод однократного отсчета. При увеличении числа отсчетов ПУ увеличивается, но при этом уменьшается скорость передачи.
СФ обеспечивает максимальное соотношение сигнал/шум, что увеличивает ПУ, но также увеличивает энергию сигнала. Таким образом, для получения наибольшей ПУ нужно использовать метод приема с помощью СФ и сигналов с большой базой, а также синхронным методом принятия решения в решающем устройстве.
Когерентный прием по обладает неплохой помехоустойчивостью, но когда параметры принимаемого сигнала нам заранее не известны, то данный КГ прием является неприемлемым.