| Скачать .docx |
Курсовая работа: Синтез счетчиков импульсов
Министерство образования Российской Федерации
Пермский Государственный технический университет
Кафедра: Автоматики и телемеханики
Курсовой проект по курсу
«Электроника»
Тема:
Синтез сч е тчиков импульсов
Выполнил: студент группы
КРЭС-06 Журавлёв А.А.
Проверил: доцент кафедры АТ
Кропачев Г.В.
Пермь 2008 г.
Задание
Введение
1. Теоретические сведения
Классификация счётчиков
Суммирующий последовательный счётчик
Вычитающий последовательный счётчик
Реверсивный последовательный счётчик
Параллельный суммирующий счётчик
2. Практическая часть работы
Выбор схемы
Составление структурной схемы счётчика
Составление функциональной схемы счётчика
3. Минимизация функций управления
Составление таблицы функционирования счётчика и определение функций переходов
Составление карт функций перехода FQ
Составление карты Карно функций управления входов для каждого триггера счётчика
Составление минимизированных логических уравнений
Выбор элементной базы
4. Разработка принципиальной схемы
Формирователь импульсов
Блок индикации
Разработка КСУ (комбинационной схемы управления)
Общий вывод
Список используемой литературы
Приложения
Спроектировать двоично-десятичный суммирующий счетчик, работающий в прямом коде 2-4-2-1, обеспечивающий состояния, указанные в колонке №4 методических указаний, и параметры
U0=0.5 (В)
U1=2.7 (В)
fmax=20 (МГц)
Iпотр=30 (мА)
с индикацией на светодиодах.
Приобретение навыков структурного проектирования цифровых устройств словарным методом и навыков самостоятельной работы.
С развитием электроники появился такой класс электронной техники, как цифровая. Эта техника предназначена для формирования, обработки и передачи электрических импульсных сигналов и перепадов напряжения и тока, а также для управления информацией и её хранения. Цифровые устройства занимают доминирующее место во многих областях науки и техники, что обусловлено существенно меньшим потреблением энергии от источника питания, более высокой точностью, меньшей критичностью к изменениям внешних условий, большей помехоустойчивостью. Цифровая техника включает в себя такие устройства как триггеры, регистры, счётчики, комбинационные устройства, программируемые логические интегральные схемы и др.
1. Теоретические сведения
Классификация счётчиков
Счетчиками называют устройства для подсчёта числа поступивших на их вход импульсов (команд), запоминания и хранения результата счёта и выдачи этого результата. Основным параметром счётчика является модуль счёта(емкость) Kс. Эта величина равна числу устойчивых состояний счётчика. После поступления импульсов Kс счётчик возвращается в исходное состояние. Для двоичных счётчиков Kс = 2 m, где m – число разрядов счётчика.
Кроме Kс важными характеристиками счётчика являются максимальная частота счёта fmax и время установления tуст, которые характеризуют быстродействие счётчика.
Tуст – длительность переходного процесса переключения счётчика в новое состояние: tуст = mtтр, где m – число разрядов, а tтр – время переключения триггера.
Fmax – максимальная частота входных импульсов, при которой не происходит потери импульсов.
По типу функционирования
Суммирующие
Вычитающие
Реверсивные
В суммирующем счётчике приход каждого входного импульса увеличивает результат счёта на единицу, в вычитающем – уменьшает на единицу; в реверсивных счётчиках может происходить как суммирование, так и вычитание.
По структурной организации
последовательными
параллельными
последовательно-параллельными
В последовательном счётчике входной импульс подаётся только на вход первого разряда, на входы каждого последующего разряда подаётся выходной импульс предшествующего ему разряда.
В параллельном счётчике с приходом очередного счётного импульса переключение триггеров при переходе в новое состояние происходит одновременно.
Последовательно-параллельная схема включает в себя оба предыдущих варианта.
По порядку изменения состояний
с естественным порядком счёта
с произвольным порядком счёта
По модулю счёта
двоичные
недвоичные
Модуль счёта двоичного счётчика Kc=2, а модуль счёта недвоичного счётчика Kc= 2m, где m – число разрядов счётчика.
Суммирующий последовательный счётчик
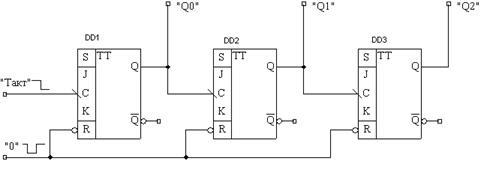
Рис.1. Суммирующий последовательный 3х разрядный счётчик.
Триггеры данного счетчика срабатывают по заднему фронту счетного импульса. Вход старшего разряда счетчика связан с прямым выходом (Q) младшего соседнего разряда. Временная диаграмма работы такого счетчика приведена на рис.2. В начальный момент времени состояния всех триггеров равны лог.0, соответственно на их прямых выходах лог.0. Это достигается посредством кратковременного лог.0, поданного на входы асинхронной установки триггеров в лог.0. Общее состояние счетчика можно охарактеризовать двоичным числом (000). Во время счёта на входах асинхронной установки триггеров в лог.1 поддерживается лог.1. После прихода заднего фронта первого импульса 0-разряд переключается в противоположное состояние – лог.1. На входе 1-разряда появляется передний фронт счетного импульса. Состояние счетчика (001). После прихода на вход счетчика заднего фронта второго импульса 0-разряд переключается в противоположное состояние – лог.0, на входе 1-разряда появляется задний фронт счетного импульса, который переключает 1-разряд в лог.1. Общее состояние счетчика – (010). Следующий задний фронт на входе 0-разряда установит его в лог.1 (011) и т.д. Таким образом, счетчик накапливает число входных импульсов, поступающих на его вход. При поступлении 8-ми импульсов на его вход счетчик возвращается в исходное состояние (000), значит коэффициент счета (КСЧ) данного счетчика равен 8.
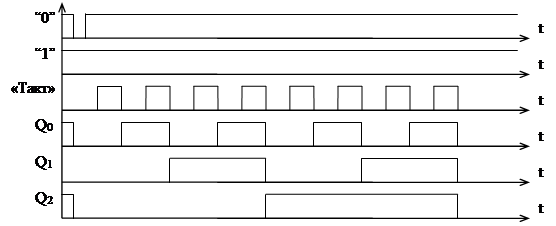
Рис. 2. Временная диаграмма последовательного суммирующего счетчика.
Вычитающий последовательный счётчик
Триггеры данного счетчика срабатывают по заднему фронту. Для реализации операции вычитания счетный вход старшего разряда подключается к инверсному выходу соседнего младшего разряда. Предварительно триггеры устанавливают в состояние лог.1 (111). Работу данного счетчика показывает временная диаграмма на рис. 4.
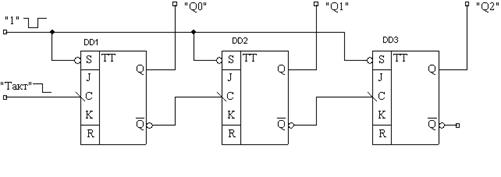
Рис. 1 Последовательный вычитающий счетчик
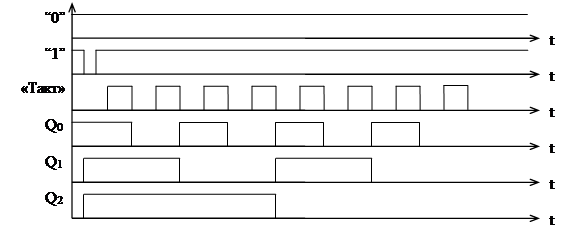
Рис. 2 Временная диаграмма последовательного вычитающего счетчика
Реверсивный последовательный счётчик
Для реализации реверсивного счетчика необходимо объединить функции суммирующего счетчика и функции вычитающего счетчика. Схема данного счетчика приведена на рис. 5. Для управления режимом счета служат сигналы «сумма» и «разность». Для режима суммирования «сумма»=лог.1, «0»-кратковременный лог.0; «разность»=лог.0, «1»-кратковременный лог.0. При этом элементы DD4.1 и DD4.3 разрешают подачу на тактовые входы триггеров DD1.2, DD2.1 через элементы DD5.1 и DD5.2 сигналов с прямых выходов триггеров DD1.1, DD1.2 соответственно. При этом элементы DD4.2 и DD4.4 закрыты, на их выходах присутствует лог.0, поэтому действие инверсных выходов никак не отражается на счетных входах триггеров DD1.2, DD2.1. Таким образом, реализуется операция суммирования. Для реализации операции вычитания на вход «сумма» подается лог.0, на вход «разность» лог.1. При этом элементы DD4.2, DD4.4 разрешают подачу на входы элементов DD5.1, DD5.2, а соответственно и на счетные входы триггеров DD1.2, DD2.1 сигналов с инверсных выходов триггеров DD1.1, DD1.2. При этом элементы DD4.1, DD4.3 закрыты и сигналы с прямых выходов триггеров DD1.1, DD1.2 никак не воздействуют на счетные входы триггеров DD1.2, DD2.1. Таким образом, реализуется операция вычитания.
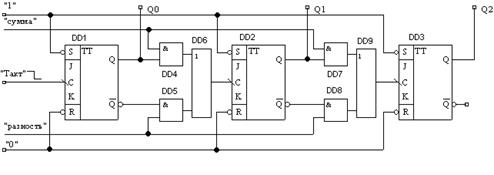
Рис. 3 Последовательный реверсивный 3-х разрядный счетчик
Для реализации данных счетчиков также можно использовать триггеры, срабатывающие по переднему фронту счетных импульсов. Тогда при суммировании на счетный вход старшего разряда надо подавать сигнал с инверсного выхода соседнего младшего разряда, а при вычитании наоборот – соединять счетный вход с прямым выходом.
Недостаток последовательного счетчика – при увеличении разрядности пропорционально увеличивается время установки (tуст) данного счетчика. Достоинством является простота реализации.
Параллельный суммирующий счётчик
Принцип действия данного счетчика заключается в том, что входной сигнал, содержащий счетные импульсы, подается одновременно на все разряды данного счетчика. А установкой счетчика в состояние лог.0 или лог.1 управляет схема управления. Схема данного счетчика показана на рис.6

Рис. 4 Суммирующий счетчик параллельного действия
Разряды счетчика – триггеры DD1, DD2, DD3.
Схема управления – элемент DD4.
Достоинство данного счетчика – малое время установки, не зависящее от разрядности счетчика.
Недостаток – сложность схемы при повышении разрядности счетчика.
Выбор схемы
Нужно спроектировать суммирующий двоично-десятичный счетчик импульсов. Для данного счётчика подойдёт схема параллельного суммирующего счётчика, т. к. этот вариант отличается хорошим быстродействием, что важно при индикации на семисегментных индикаторах, т. к. там, помимо самого счёта, учитывается время реагирования дешифратора. Я же проектирую счётчик с индикацией на светодиодах, и меня устроил бы менее «быстрый» счётчик, но лучше сделать счётчик как можно более универсальным (например, чтобы работал с разным вариантом индикации), да и более высокая скорость срабатывания лучше, чем низкая, поэтому я выбрал схему параллельного счётчика.
Составление структурной схемы счётчика
Структурная схема – совокупность блоков счётчика, выполняющих какую-либо функцию и обеспечивающих нормальную работу счётчика. На рисунке 7 показана структурная схема счётчика.

Рис. 7 Структурная схема счётчика
Блок управления выполняет функцию подачи сигнала и управления триггерами.
Блок счёта предназначен для изменения состояния счетчика и сохранения этого состояния.
Блок индикации выводит информацию для зрительного восприятия.
Составление функциональной схемы счётчика
Функциональная схема – внутренняя структура счётчика.
Определим оптимальное количество триггеров для недвоичного счётчика с коэффициентом счёта Кс=10.
M = log 2 (Кс) = 4.
M = 4 значит для реализации двоично-десятичного счётчика необходимо 4 триггера.
3. Минимизация функций управления
Составление таблицы функционирования счётчика и определение функций переходов
Таблица функционирования отображает состояния счетчика до переключающего сигнала и после в зависимости от заданного кода(2-4-2-1), а также функции перехода, показывающие, как изменится состояние. При использовании четырёх разрядов можно закодировать 16 возможных комбинаций цифр двоичной системы счисления, для кодировки 10 цифр достаточно 10 комбинаций. Чтобы исключить некоторые комбинации (в зависимости от кода) используют разные виды кодировки. В коде 2-4-2-1 (код Айкена) исключаются такие комбинации как:
1000,1001,1010,1011,1100,1101
И остаются комбинации:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
В нижней строке указана цифра десятичной системы счисления, которой соответствует данная комбинация. Таблица функционирования для суммирующего двоично-десятичного счётчика, работающего в прямом коде 2-4-2-1, будет выглядеть так:
| Состояние счётчика | Функции перехода | ||||||||||||
| Предыдущее | Последующее | ||||||||||||
| № | Qn3 | Qn2 | Qn1 | Qn0 | Qn+13 | Qn+12 | Qn+11 | Qn+10 | FQ3 | FQ3 | FQ3 | FQ3 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ▲ | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ▲ | ▼ | |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | ▲ | |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | ▲ | ▼ | ▼ | |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ▲ | |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | ▲ | ▼ | |
| 6 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | ▲ | |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | ▲ | 1 | 1 | ▼ | |
| 8 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ▲ | |
| 9 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ▼ | ▼ | ▼ | ▼ | |
Где значения функций перехода:
0 – переход из LOG”0” в LOG”0”
1 – переход из LOG”1” в LOG”1”
▲ – переход из LOG”0” в LOG”1”
▼ – переход из LOG”1” в LOG”0”
№ - цифра десятичной системы счисления.
Составление карт функций перехода FQ
Эти карты показывают, какое значение принимает функция перехода для данного триггера при определенной комбинации значений на выходах всех триггеров. Карты функций перехода потребуются в дальнейшем для составления функций управления входами триггеров.
Карты состояний счётчика:
| Q1Q0 | ||||||||||
| 00 | 01 | 10 | 11 | |||||||
| Q3Q2 | 00 | 0 | 1 | 2 | 3 | |||||
| 01 | 4 | 5 | 6 | 7 | ||||||
| 10 | - | - | - | - | ||||||
| 11 | - | - | 8 | 9 | ||||||
| Q1 | Q1* | |||||||||
| Q2* | - | - | - | - | Q3 | |||||
| Q2 | 8 | 9 | - | - | ||||||
| 6 | 7 | 5 | 4 | Q3* | ||||||
| Q2* | 2 | 3 | 1 | 0 | ||||||
| Q0* | Q0 | Q0* | ||||||||
Карты функций перехода:
| FQ3 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | 1 | ▲ | - | - | |
| 0 | ▲ | 0 | 0 | Q3* | |
| Q2* | 0 | 0 | 0 | 0 | |
| Q0* | Q0 | Q0* | |||
| FQ2 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | 1 | ▼ | - | - | |
| 1 | 1 | 1 | 1 | Q3* | |
| Q2* | 0 | ▲ | 0 | 0 | |
| Q0* | Q0 | Q0* | |||
| FQ0 | Q1 | Q1* | ||||||||
| Q2* | - | - | - | - | Q3 | |||||
| Q2 | ▲ | ▼ | - | - | ||||||
| ▲ | ▼ | ▼ | ▲ | Q3* | ||||||
| Q2* | ▲ | ▼ | ▼ | ▲ | ||||||
| Q0* | Q0 | Q0* | ||||||||
| FQ1 | Q1 | Q1* | ||||||||
| Q2* | - | - | - | - | Q3 | |||||
| Q2 | 1 | ▼ | - | - | ||||||
| 1 | 1 | ▲ | 0 | Q3* | ||||||
| Q2* | 1 | ▼ | ▲ | 0 | ||||||
| Q0* | Q0 | Q0* | ||||||||
В левом верхнем углу каждой карты указано, для какого триггера составлялась карта.
Составление карты Карно функций управления входов для каждого триггера счётчика
Карты Карно составляются в соответствие со словарём перехода триггера. Для данного счётчика я буду использовать JK-триггеры, т. К. они самые универсальные. Словарь перехода для JK-триггера выглядит следующим образом:
| FQ | J-вход | K-вход |
| 0 | 0 | X |
| 1 | X | 0 |
| ▲ | 1 | X |
| ▼ | X | 1 |
Используя этот словарь, получим:
для триггера T3:
| J3 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | X | X | - | - | |
| 0 | 1 | 0 | 0 | Q3* | |
| Q2* | 0 | 0 | 0 | 0 | |
| Q0* | Q0 | Q0* | |||
| K3 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | 0 | 1 | - | - | |
| X | X | X | X | Q3* | |
| Q2* | X | X | X | X | |
| Q0* | Q0 | Q0* | |||
для триггера T2:
| J2 | Q1 | Q1* | |||||||
| Q2* | - | - | - | - | Q3 | ||||
| Q2 | X | X | - | - | |||||
| X | X | X | X | Q3* | |||||
| Q2* | 0 | 1 | 0 | 0 | |||||
| Q0* | Q0 | Q0* | |||||||
| K2 | Q1 | Q1* | |||||||
| Q2* | - | - | - | - | Q3 | ||||
| Q2 | 0 | 1 | - | - | |||||
| 0 | 0 | 0 | 0 | Q3* | |||||
| Q2* | X | X | X | X | |||||
| Q0* | Q0 | Q0* | |||||||
для триггера T1:
| J1 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | X | X | - | - | |
| X | X | 1 | 0 | Q3* | |
| Q2* | X | X | 1 | 0 | |
| Q0* | Q0 | Q0* | |||
| K1 | Q1 | Q1* | |||
| Q2* | - | - | - | - | Q3 |
| Q2 | 0 | 1 | - | - | |
| 0 | 0 | X | X | Q3* | |
| Q2* | 0 | 1 | X | X | |
| Q0* | Q0 | Q0* | |||
для триггера T0:
| J0 | Q1 | Q1* | ||||
| Q2* | - | - | - | - | Q3 | |
| Q2 | 1 | X | - | - | ||
| 1 | X | X | 1 | Q3* | ||
| Q2* | 1 | X | X | 1 | ||
| Q0* | Q0 | Q0* | ||||
| K0 | Q1 | Q1* | ||||
| Q2* | - | - | - | - | Q3 | |
| Q2 | X | 1 | - | - | ||
| X | 1 | 1 | X | Q3* | ||
| Q2* | X | 1 | 1 | X | ||
| Q0* | Q0 | Q0* | ||||
Составление минимизированных логических уравнений
В картах Карно выделены клетки, которые описываются наиболее простыми логическими уравнениями, и охватывающие все единичные состояния триггеров. Исходя из этого, составим минимизированные логические уравнения функций управления:
J3 = Q0Q1Q2 K3 = Q0Q1 Q – прямое значение (LOG”1”)
J2 = Q0Q1 K2 = Q0Q1Q3 ‘Q – инверсное значение (LOG”0”)
J1 = Q0’Q1 K1 = Q0Q1Q3 + Q0’Q2
J0 = 1 K0 = 1
Преобразуем функцию K1 = Q0Q1Q3 + Q0’Q2 по теореме Де-Моргана:
K1 = [‘(Q0Q1Q3)] [‘(Q0’Q2)]
K1 = ‘{[‘(Q0Q1Q3)] [‘(Q0’Q2)]}
После преобразований получим такие уравнения:
J3 = Q0Q1Q2 K3 = Q0Q1 Q – прямое значение
J2 = Q0Q1 K2 = Q0Q1Q3 ‘Q – инверсное значение
J1 = Q0’Q1 K1 = ‘{[‘(Q0Q1Q3)] [‘(Q0’Q2)]}
J0 = 1 K0 = 1
Для разработки принципиальной схемы необходимо выбрать тип логики, на которой будет реализован счётчик. Заданные параметры и параметры микросхем подходящей серии показаны в таблице:
| Параметр | В задании | Серия К555 |
| U1, В | 2,7 | >=2.5 |
| U0, В | 0,5 | <=0.5 |
| Iпотр, мА | 30 | 7*2=14 |
| fmax, МГц | 20 | 20 |
Из таблицы видно, что для таких заданных параметров подходит серия К555 ТТЛШ логики.
4. Разработка принципиальной схемы
Формирователь импульсов
Формирователь импульсов – устройство, необходимое для устранения дребезга контактов, возникающего при замыкании механических контактов, который может привести к неправильной работе схемы.
На рисунке 9 приведены схемы формирователей импульсов от механических контактов.
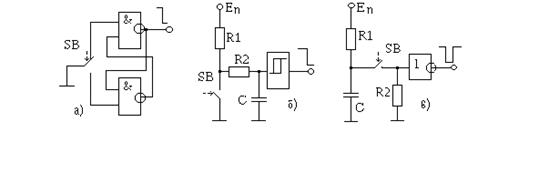
Рис. 9 Формирователи импульсов от механических контактов.
Выберем схему 9.а) из-за простоты исполнения.
Для отображения результата счёта необходимо использовать светодиоды. Чтобы осуществить такой вывод информации можно воспользоваться простейшей схемой. Схема блока индикации на светодиодах приведена на рисунке 10.
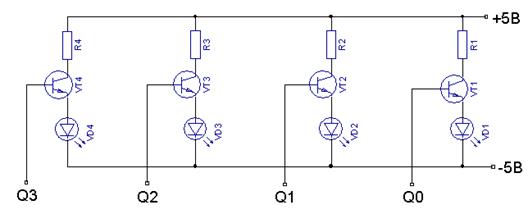
Рис. 10 Блок индикации на светодиодах.
Разработка КСУ (комбинационной схемы управления)
Для реализации данного счётчика из серии ТТЛШ микросхем К555 я выбрал:
две микросхемы К555ТВ9 (2 JK-триггера с установкой)
одну микросхему К555ЛА4 (3 элемента 3И-НЕ)
две микросхемы К555ЛА3 (4 элемента 2И-НЕ)
одну микросхему К555ЛН1 (6 инверторов)
Данные микросхемы обеспечивают минимальное количество корпусов на печатной плате.
Принципиальная схема КП.2421.ПС, спецификация КП.2421.01, чертежи монтажной схемы и печатной платы, а также функциональная схема находятся в приложениях.
Согласно заданию я рассчитал и спроектировал двоично-десятичный суммирующий счетчик, работающий в прямом коде 2-4-2-1, с индикацией на светодиодах и проверил его работоспособность на лабораторных стендах.
Во время работы над курсовым проектом я приобрел новые навыки по проектированию и разработке цифровых устройств, а также укрепил теоретические знания, приобретенные мной на лекциях по электронике.
Список используемой литературы
И.И. Бобров «Импульсные и цифровые устройства», Пермь 2005г.
Справочник «Интегральные микросхемы» Б.В. Тарабрин, Л.Ф. Лунин, Ю.Н. Смирнов и др., Радио и связь, Москва 1984г.
В Л. Шило «Популярные цифровые микросхемы», Радио и связь, Москва 1987г.
А.С. Партин, В.Г. Борисов «Введение в цифровую технику», Радио и связь, Москва 1987г.
Б.И. Горошков «Элементы радиоэлектронных устройств», Радио и связь, Москва 1988г.
Методические рекомендации «Синтез счётчиков сигналов» Ю. В. Панов, Т. С. Леготкина, Пермь 1990г.
Также использованы материалы сайта www.qrz.ru и электронный «Справочник по цифровым логическим микросхемам ТТЛ, ТТЛШ, ЭСЛ типов, 1 часть».