Главная / Рефераты / Коммуникации и связь

Курсовая работа: Дослідження властивостей лiнiйних динамічних кіл

Вступ

В даній курсовій роботі ми розглянемо перетворення сигналів довільної форми лінійними динамічними колами першого порядку в часовій та частотній областях. В часовій області ми розглянемо визначення перехідної характеристики кола (класичним або операторним методами) та реакції кола на сигнал довільної форми методом інтеграла згортки (Дюамеля). В частотній області за допомогою комплексно-частотної функції кола дослідимо основні частотні характеристики (АЧХ, ФЧХ, характеристику групового часу запізнення), визначимо граничні частоти та смугу пропускання.

Метою роботи є освоєння різних методів, для знаходження реакції кола на вхідний сигнал довільної форми, та переконання на практиці, що при використанні, ці методи є ефективними та правильними.

При дослідженні характеру зміни основних частотних характеристик в залежності від зміни параметрів елементів кола проводиться якісний та кількісний аналізи процесів ,що відбуваються в колі в залежності від частоти вхідного сигналу. Визначається амплітудний та фазовий спектри вхідного сигналу та реакція на його дію.

Для наочності та зручності результати обчислень представляються в табличній та графічній формах. Таблиці та графіки наведені в курсовій роботі побудовані за допомогою пакету програм Mathcad 2003.

1.Визначення реакції кола на вхідний сигнал довільної форми методом інтеграла Дюамеля (інтеграла згортки)

Метод інтеграла Дюамеля відноситься до класу методів аналізу динамічних систем у часовій області, коли як діючий сигнал, так і властивості системи описуються функцією часу.

В основі цього методу лежать два так звані принципи:

• принцип розкладання довільного сигналу на суму так званих елементарних сигналів, яка з деякою точністю відповідає початковому сигналу;

• принцип суперпозиції: реакція лінійного кола на довільну дію є алгебраїчною сумою реакцій на окремі компоненти.

Найбільше поширення в теорії електричних кіл при розкладенні довільного сигналу мають одиничний ступінчастий σ(t) та одиничний імпульсний δ(t). Розкладання сигналу у цьому базисі є різновидом динамічного зображення довільного сигналу. Реакція на такі елементарні сигнали визначається часовими характеристиками: перехідною h(t) та імпульсною g(t) і має вигляд:

(1.1)

(1.2)

де x(t) - діючий сигнал.

Визначимо перехідну характеристику для нашого кола за допомогою операторного методу.

Так як реакція кола – напруга на виході i_вих (елемент навантаження R1), то будемо шукати операторну функцію як передаточну провідність – Y_пер (р). Для цього побудуємо операторну схему заміщення кола (рис. 1.1, а).

Рисунок 1.1 – Схема заміщення електричного кола

Перетворимо трикутник в зірку: ;

; (рис. 1.1, б). Через елемент струм не протікає, тому, оскільки у нас нульові початкові умови, за правилом свого плеча:

(1.3)

Тоді:

(1.4)

Або:

Звідси маємо зображення перехідної характеристики:

(1.5)

Де – коефіцієнт згасання кола, – частота резонансу контуру, – постійна часу кола.

Оскільки , тому перехідний процес, а отже і перехідна характеристика, повинні мати аперіодичний характер.

Переходячи від зображення (1.5) до оригіналу перехідної характеристики маємо:

(1.6)

де , ,

, .

Імпульсна характеристика як похідна по часу від перехідної:

(1.7)

Графік перехідної характеристики показано на рис 1.2,а; імпульсної – на рис 1.2,б. Результати розрахунків і вказані в таблиці 1.1.

Таблиця 1.1 Значення перехідної та імпульсної характеристик


0	10	-9.965
3,00000	4.216	-3.03
6,00000	2.37	-1.059
9,00000	1.658	-0.475
12,0000	1.295	-0.283
15,0000	1.056	-0.205
18,0000	0.874	-0.162
21,0000	0.728	-0.133
24,0000	0.607	-0.11
27,0000	0.506	-0.092
30,0000	0.422	-0.076

Рисунок 1.2 – Перехідна (а) та імпульсна (б) характеристики

Тепер знайдемо реакцію на сигнал довільної форми (рис. А.2).

Ураховуючи те, що діючий сигнал має різні функціональні залежності від часу на різних часових відрізках, визначимо реакцію на цей сигнал методом припасовування.

Розглянемо проміжок часу , де .

На цьому проміжку вхідний сигнал: .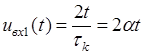

Згідно з методом перехідних характеристик реакція має вигляд:

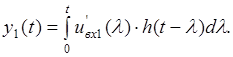
Далі розглянемо проміжок часу , де .

На цьому проміжку математична модель вхідного сигналу має вигляд:

Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:

На проміжку часу вхідний сигнал: .

Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:

Повна реакція кола на діючий сигнал:

(1.8)

Графік реакції на рис. 1.3, а числові дані в таблиці 1.2.

Таблиця 1.2 Значення реакції кола на трикутний імпульс


0	0
3	38.119
6	67.02
9	32.094
12	-12.196
15	-27.006
18	-19.127
21	-13.721
24	-10.003
27	-7.435
30	-5.654
33	-4.409
36	-3.532
39	-2.906
42	-2.454
45	-2.12

Рисунок 1.3 – Значення реакції кола на трикутний імпульс

Перевіримо отриманий результат графічною інтерпретацією процедури розрахунків методом інтеграла Дюамеля. Використаємо для цього формулу інтеграла Дюамеля через імпульсну характеристику (1.1). Відповідно до формули (1.1) миттєвим значенням реакції для моментів часу відповідає площа, яка є алгебраїчною сумою двох площ: перша – це площа фігури, яка обмежується віссю абсцис і графіком функції, отриманої в результаті добутку зсунутого в точку на осі абсцис дзеркального відображення відносно осі координат неперервної складової (без стрибка) імпульсної характеристики та діючого сигналу; друга – пропорційна добутку початкового значення перехідної характеристики на миттєве значення .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії імпульсної характеристики на рис.1.4,а.

Очевидно, що добуток цих функцій дорівнює дорівнює нулю, а отже дорівнює дорівнює нулю і перша площа . Таким чином, початкове значення реакції також дорівнює нулю .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії імпульсної характеристики на рис.1.4,б. Реакція в цей момент часу зростає. Площа дорівнює .

Рисунок 1.4

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії імпульсної характеристики (рис.1.5,а). Для даного моменту часу , а отже площа від’ємна [4].

Рисунок 1.5

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії імпульсної характеристики (рис.1.5,б). Для даного часу друга площа є від’ємною, але значно меншою ніж у попередніх випадках. Очевидно, що при подальшому зсуві копії імпульсної характеристики, виходячи з її виду, площа буде зменшуватися, все більше наближаючись до нуля. А отже, знайдена нами реакція обчислена вірно.

2. Визначення частотних характеристик заданого кола

Вимоги на частотні властивості системи та її складові визначаються через відповідні параметри так званих частотних характеристик.

Частотні характеристики отримують на основі комплексної частотної функції (КЧФ) кола:

(2.1)

де - амплітуда діючого комплексного експоненціального сигналу , - амплітуда реакції такого ж виду, як і дія є у загальному випадку величинами комплексними та функціями дійсної частоти чи .

Ці амплітуди можуть бути виражені через параметри гармонічної реакції та дії: - комплексна амплітуда дії, - комплексна амплітуда реакції.

Залежність виду називають амплітудно-частотною характеристикою (АЧХ) лінійного кола, а - його фазо-частотною характеристикою (ФЧХ). Ця пара характеристик лінійного динамічного кола визначає його властивості в області дійсної частоти чи в усталеному гармонічному режимі.

Отже, знаходження частотних характеристик кола зводиться до визначення комплексної частотної функції кола.

Реакція лінійного електричного кола на гармонічний сигнал (дію) в моменти часу, коли всі процеси визначаються тільки діючим сигналом, теж є гармонічною, причому амплітуда реакції .

Графічне зображення комплексної частотної функції , яка зветься амплітудно-фазовою характеристикою або частотним годографом - це геометричне місце точок на комплексній площині кінця радіус-вектора довжиною, що дорівнює модулю КЧФ , та кутом нахилу до дійсної осі, що дорівнює значенню її аргументу, для відповідних значень частоти при її зміні від нуля до нескінченості.

Амплітудно-частотна характеристика - це модуль

КЧФ для різних значень частоти .

Фазо-частотна характеристика - аргумент КЧФ.

Характеристика затримки чи групового часу запізнення характеризує швидкість зміни ФЧХ:

Дійсна частина КЧФ — дійсна АЧХ, а її уявна частина - уявна АЧХ.

Логарифмічна АЧХ, що виражається в неперах

або в децибелах

Розглянемо наше коло та визначимо його частотні характеристики і вплив на них параметрів деяких елементів кола, ґрунтуючись на комплексній частотній функції у вигляді коефіцієнта передачі напруги .

Аналогічно до попереднього пункту знаходимо із урахуванням позначень для коефіцієнта згасання та частоти резонансу:

(2.2)

Знайдемо амплітудно-частотну характеристику кола (АЧХ) як модуль комплексної частотної функції, тому (із урахуванням числових значень параметрів елементів)

(2.3)

Фазо-частотна характеристика (ФЧХ) даного кола як аргумент визначеної комплексної частотної функції:

.(2.4)

Характеристику групового часу запізнення отримаємо як похідну по частоті з від’ємним знаком від фазо-частотної характеристики (2.4):

(2.5)

Графіки АЧХ та ФЧХ на рис.2.1, рис.2.2 відповідно, а характеристик групового часу запізнення на рис.2.3. Значення частотних характеристик наведені у таблиці 2.1.

Таблиця 2.1 Значення АЧХ, ФЧХ та характеристики групового часу запізнення для різних значень частоти.


0	0	1.571	0
1	0.667	0.653	27.775
2	0.86	0.433	16.191
3	0.929	0.311	9.016
4	0.958	0.24	5.537
5	0.972	0.195	3.697
6	0.98	0.164	2.629
7	0.985	0.141	1.959
8	0.989	0.124	1.514
9	0.991	0.11	1.204
10	0.993	0.099	0.98

Рисунок 2.1 – Амплітудно-частотна характеристика

Рисунок 2.2– Фазо-частотна характеристика

Рисунок 2.3 – Характеристика групового часу запізнення

Амплітудно-фазова характеристика (частотний годограф). Ця характеристика містить в собі АЧХ та ФЧХ. За означенням, частотний годограф – це крива, яку описує кінець вектора, довжина якого дорівнює значенню АЧХ при визначеному значенні частоти ω, а кут нахилу до осі абсцис – значенню ФЧХ при тому ж значенні частоти.

Для побудови частотного годографа скористаємось алгебраїчним представленням комплексної частотної функції:

(2.6)

де А(ω) та В(ω) – відповідно дійсна та уявна частини КЧФ. На дійсній осі відкладаються значення А(ω), а на уявній осі комплексної площини – значення В(ω) [2]. Графічне зображення КЧФ в координатах В та А на рис.2.4. Числові дані наведені у таблиці 2.2.

Таблиця 2.2 Дані для побудови частотного годографа.


0	0	0
1	0.53	40.51
2	0.781	36.068
3	0.884	28.408
4	0.93	22.771
5	0.954	18.819
6	0.967	15.97
7	0.976	13.842
8	0.981	12.2
9	0.985	10.9
10	0.988	9.845
	1	0

Рисунок 2.4 – Частотний годограф

Визначимо логарифмічні частотні характеристики. Для аргументу (частоти) логарифмічною одиницею виберемо декаду, а для функцій (логарифмічних характеристик) – децибел. За означенням ЛАЧХ та ХЗ визначаються відповідно як:

(2.7)

(2.8)

Для отримання табличних даних та для побудови графіка логарифмічної фазо-частотної характеристики (ЛФЧХ) скористаємось виразом для фазо-частотної характеристики. Графік цієї функції зобразимо на рисунку 2.6. Результати розрахунків наведені в таблиці 2.3. Графік логарифмічної АЧХ та характеристики затухання на рис 2.5.

Таблиця 2.3 Дані для побудови частотного годографа.


0	-133.979	133.979	1.571
1	-113.979	113.979	1.571
2	-93.979	93.979	1.571
3	-73.979	73.979	1.57
4	-53.98	53.98	1.567
5	-33.991	33.991	1.529
6	-14.965	14.965	1.2
7	-3.52	3.52	0.653
8	-0.063	0.063	0.099

Рисунок 2.4 – Логарифмічна АЧХ(а) та характеристика затухання(б)

Рисунок 2.5 – Логарифмічна ФЧХ

Знайдемо граничні частоти умовної смуги пропускання на рівні 3дБ, а потім значення характеристики групового часу запізнення на цих частотах.

У нашому випадку йдеться про одну смугу пропускання та дві смуги затримки: одна в області нижніх, а друга в області верхніх частот. Визначимо максимальне значення АЧХ: К_u (ω)=1. Для знаходження граничних частоти необхідно розв’язати рівняння:

Звідси ω_н.гр. = 1.136·107⁶ рад/с.

Таким чином умовною смугою пропускання є діапазон [2.986·10⁶ ;]. Таким чином має місце фільтр високих частот (ФВЧ).

Знаючи граничну частоту, визначимо характеристику групового часу затримки на рівні 3дБ: Ψ(ω_н.гр. )= 2.651·10^- ⁸ с.

3. Дослідження залежності частотних характеристик АЧХ та ФЧХ від зміни параметрів навантаження R1 та елемента С1

Оцінимо вплив на АЧХ та ФЧХ елементів C1 таR1 кола. Спочатку зробимо якісне , а потім кількісне оцінювання.

Основу якісного аналізу складає схема кола без будь-яких розрахунків. Задане коло можна розглядати як розподілювач напруги з резистивним елементом R1 та гілкою, що складається з елементів C1, C1, R2 (гілка Г).

На нульовій частоті опір ємнісного елемента дорівнює нескінченності, отже ємнісні елементи C1 можна вважати розривом кола, на цих елементах падає вся вхідна напруга, а через навантаження R1 струм взагалі не протікає, тому на нульовій частоті АЧХ дорівнює нулю .

Опір ємнісних елементів зменшується за гіперболічним законом. На високій частоті елементи C1 можна вважати закоротками, отже весь вхідний струм портікає через резистивний елемент навантаження, АЧХ встановлюється на рівні що дорівнює значенню опору резистивного елемента навнтаження.

На малих частотах опори ємнісних елементів є великими, тому на гілці Г падає вся вхідна напруга, з ростом частоти опір ємнісного елемента С1 зменшується і через елемент навантаження R1 починає протікати струм, в результаті АЧХ зростає. На вищих частота опір ємнісних елементів зменшується, і опір гілки Г прямує до нуля, відповідно вся вхідна напруга падає на елементі R1 кола.

При збільшенні опору елемента навантаження R1 на ньому падає більша напруга, відповідно АЧХ досягає більших значень.

Різниця початкових фаз реакції і діючого сигналу буде переважно визначатися тільки властивостями гілки Г.

При збільшенні ємності елемента С1 його реактивний опір зменшується на нижчих частотах, тому більший струм починає протікати через елемент навантаження АЧХ досягає більших значень на нижчих частотах, зростає крутіше.

Відповідно до попереднього ФЧХ приймає тільки додатні значення (схема є резистивною на великих частотах).

Підтвердимо наш якісний аналіз кількісними розрахунками (таблиці 3.1 і 3.2, рис. 3.1-3.4).

Таблиця 3.1 Вплив елементу С₁ на частотні характеристики.

	С₁ =0.01 нФ		С₁ =0.1 нФ		С₁ =1 нФ
	K_umin (ω)	φ_min (ω)	K_u (ω)	φ_C1 (ω)	K_umax (ω)	φ_max (ω)
рад/мкс	рад	рад	рад
0	0.000	1.571	0.000	1.571	0.000	1.571
1	0.020	1.529	0.179	1.200	0.667	0.653
2	0.040	1.488	0.289	0.987	0.860	0.433
3	0.059	1.448	0.359	0.886	0.929	0.311
4	0.078	1.408	0.416	0.833	0.958	0.240
5	0.097	1.370	0.466	0.798	0.972	0.195
6	0.115	1.332	0.513	0.767	0.980	0.164
7	0.132	1.297	0.556	0.738	0.985	0.141
8	0.148	1.263	0.597	0.710	0.989	0.124
9	0.164	1.231	0.633	0.681	0.991	0.110
10	0.179	1.200	0.667	0.653	0.993	0.099

Рисунок 3.1. Залежність АЧХ від опору елемента R₁ .

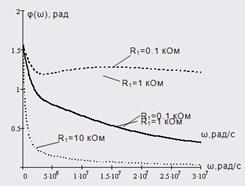
Рисунок 3.2. Залежність ФЧХ від опору елемента R₁ .

Таблиця 3.2 Вплив елементу R₁ на частотні характеристики.

	R₁ =0.1 кОм		R₁ =1 кОм		R₁ =10 кОм
	К_umin (ω)	φ_min (ω)	К_u (ω)	φ(ω)	К_umax (ω)	φ_max (ω)
рад/мкс	рад	рад	рад
0	0.000	1.571	0.000	1.571	0.000	1.571
1	0.019	1.358	0.179	1.200	0.820	0.442
2	0.033	1.235	0.289	0.987	0.886	0.259
3	0.043	1.192	0.359	0.886	0.911	0.198
4	0.052	1.188	0.416	0.833	0.929	0.166
5	0.061	1.199	0.466	0.798	0.942	0.145
6	0.069	1.215	0.513	0.767	0.953	0.129
7	0.078	1.230	0.556	0.738	0.962	0.117
8	0.087	1.243	0.597	0.710	0.968	0.106
9	0.096	1.253	0.633	0.681	0.973	0.097
10	0.105	1.261	0.667	0.653	0.977	0.089

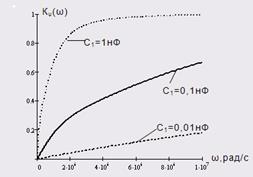
Рисунок 3.3. Залежність АЧХ від ємності елемента С₁ .

Рисунок 3.4. Залежність ФЧХ від ємності елемента С₁ .

4. Обчислення спектру заданого сигналу та спектру реакції на цей сигнал

4.1 Розрахунок спектру сигналу по його часовому представленню

Для заданого вхідного сигналу рис. 4 виконаємо пряме перетворення Фур’є:

Тоді спектр вхідного сигналу визначається наступним чином:

Розкладемо одержаний вираз на дійсну та уявну частини використовуючи формулу Ейлера:

Враховуючи, що , розраховано в першому пункті. Визначимо амплітудний та фазовий спектр вхідного сигналу:

Значення цих функцій в залежності від частоти приведені в табл. 4.1, графіки, відповідно, на рис. 4.1 та рис. 4.2.

Таблиця 4.1


0	0	0
1	0.225	0.774
2	0.409	-0.025
3	0.518	-0.829
4	0.541	1.5
5	0.484	0.674
6	0.373	-0.171
7	0.239	-1.044
8	0.114	1.183
9	0.016	0.209
10	0.05	-0.836

4.2 Розрахунок спектру реакції

Спектр вихідного сигналу знайдемо за формулою:

де: - комплексна частотна функція заданого кола, розрахована в пункті 1. Таким чином спектр реакції:

де

– фазо-частотна характеристика (ФЧХ) даного кола як аргумент визначеної комплексної частотної функції.

Амплітудний спектр вихідного сигналу розраховуємо за формулою:

Частотний спектр вихідного сигналу розраховуємо за формулою:

Значення цих функцій в залежності від частоти приведені в табл. 4.2, графіки, відповідно, на рис. 4.3 та рис. 4.4.

Таблиця 4.2


0	0	1.571
1	1.504	1.427
2	3.517	0.408
3	4.812	-0.518
4	5.18	1.74
5	4.709	0.869
6	3.657	-0.07
7	2.357	-0.903
8	1.123	1.306
9	0.158	0.319
10	0.492	-0.737

Рисунок 4.3 – Амплітудний спектр вихідного сигналу

Рисунок 4.4 – Фазовий спектр вихідного сигналу

Висновки

В цій курсовій роботі ми дослідили вплив лінійного динамічного кола на сигнал довільної форми. Визначили реакцію кола на заданий сигнал методом інтеграла Дюамеля (згортки) та навели графічну та табличну інтерпретацію розрахунків.

В ході виконання роботи ми визначили характер даного кола, а також діапазон частот які воно відфільтровує.

За допомогою визначеної комплексної частотної функції були знайдені такі характеристики: АЧХ, ФЧХ, характеристика групового часу запізнення, логарифмічні АЧХ та ФЧХ і характеристика затухання, побудовані їх графіки, наведені таблиці відповідних значень.

Ми також визначили, як змінюються амплітудо частотна та фазочастотна характеристики при зміні параметра елемента навантаження та додаткового елемента для дослідження частотних характеристик даного кола.

Для вхідного та вихідного сигналу побудували спектр амплітуд та спектр фаз. Для точного результату та для побудови графіків розрахунки проводили за допомогою математичного пакету програм Mathcad 2003.

Додаток

Завдання на курсову роботу

Таблиця 1 Параметри елементів кола

R1, кОм	R2, кОм	C1, нФ
1	4,3	0.1

Рисунок А.1 – Схема електричного кола

Рисунок А.2 – Графік вхідного сигналу