| Скачать .docx |
Реферат: Расчет настроек автоматического регулятора 2
Министерство общего и профессионального образования РФ
Пермский государственный технический университет
Березниковский филиал
Курсовая работа
по предмету: Автоматизация технологических процессов и
производств.
Тема: Расчет настроек автоматического регулятора.
Выполнил: ст-т гр. АТП-93
Панкина Н.В.
Проверил: Бильфельд Н. В.
г. Березники, 1998
Содержание.
1. Координаты кривых разгона.
1.1 Схемы для Ремиконта.
1.2 Координаты и график кривой разгона по возмущению.
1.3 Координаты и график кривой разгона по заданию.
1.4 Координаты и график кривой разгона по управлению.
2. Интерполяция по 3 точкам.
2.1 Линейное сглаживание и график кривой разгона по возмущению.
2.2 Линейное сглаживание и график кривой разгона по заданию.
2.3 Линейное сглаживание и график кривой разгона по управлению.
3. Нормирование кривых разгона.
3.1 Нормирование кривой разгона по возмущению.
3.2 Нормирование кривой разгона по заданию.
3.3 Нормирование кривой разгона по управлению.
4. Аппроксимация методом Симою.
4.1 По возмущению.
4.2 По заданию.
4.3 По управлению.
5. Проверка аппроксимации методом Рунге - Кутта.
5.1 По возмущению.
5.2 По заданию.
5.3 По управлению.
5.4 Сравнение передаточных функций.
5.5 Сравнение кривых разгона.
6. Расчет одноконтурной АСР методом Роточа.
Координаты кривой разгона
С помощью программы связи ЭВМ с контроллером снимаем координаты кривой разгона.
Для этого сначала поочередно программируем Ремиконт:
1. по возмущению
2. по заданию
3. по управлению
объект 2-го порядка
01 1.1 21 1.2 21 1.3
313 311 312
1 11 1 11 1 11
Н1=-100 Н1=-100 Н1=-100
Н2=100 Н2=100 Н2=100
к6= к6=1 к6=1
Т1= Т1= Т1= по заданию
Т1= Т1= Т1= по возмущению
Объект 3-го порядка с запаздыванием по управлению
01 1.1 21 1.2 21 1.3 21 1.4 26 1.5
315 311 312 313 314
1 11 1 11 1 11 1 11 1 11
Т1= Т1= Т1= Т1= Т1=
 |
В программе тренды меняя задание добиваемся устойчивости систем.
После того как системы установились приступаем к проведению эксперемента. Для этого устанавливаем алгоблок 11 с которого будем снимать кривую разгона, алгоблок 11 на который будем подавать скачек, амплитуду скачка 10 и интервал времени 0,5.
После просмотра полученных точек кривых разгона удаляем одинаковые.
И строим соответствующие графики.
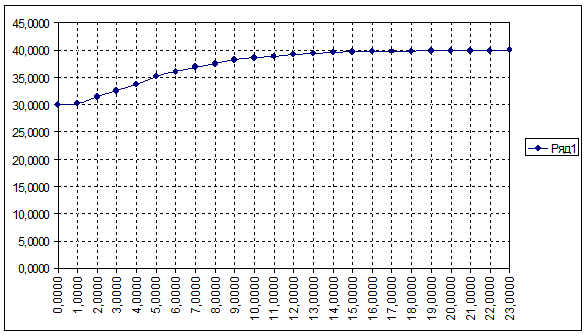
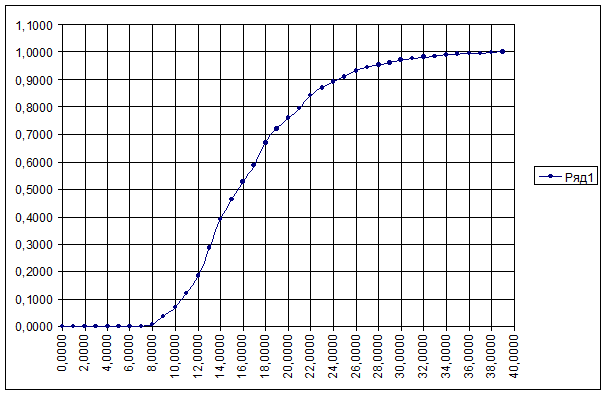
Координаты и график кривой разгона по возмущению.
| 1 | 0,0000 | 30,0000 |
| 2 | 1,0000 | 30,2000 |
| 3 | 2,0000 | 31,5000 |
| 4 | 3,0000 | 32,6000 |
| 5 | 4,0000 | 33,7000 |
| 6 | 5,0000 | 35,2500 |
| 7 | 6,0000 | 36,1000 |
| 8 | 7,0000 | 36,8500 |
| 9 | 8,0000 | 37,4500 |
| 10 | 9,0000 | 38,2000 |
| 11 | 10,0000 | 38,5500 |
| 12 | 11,0000 | 38,8500 |
| 13 | 12,0000 | 39,2000 |
| 14 | 13,0000 | 39,4000 |
| 15 | 14,0000 | 39,5500 |
| 16 | 15,0000 | 39,6500 |
| 17 | 16,0000 | 39,7500 |
| 18 | 17,0000 | 39,8000 |
| 19 | 18,0000 | 39,8500 |
| 20 | 19,0000 | 39,9000 |
| 21 | 20,0000 | 39,9500 |
| 22 | 21,0000 | 39,9500 |
| 23 | 22,0000 | 39,9500 |
| 24 | 23,0000 | 40,0000 |
|
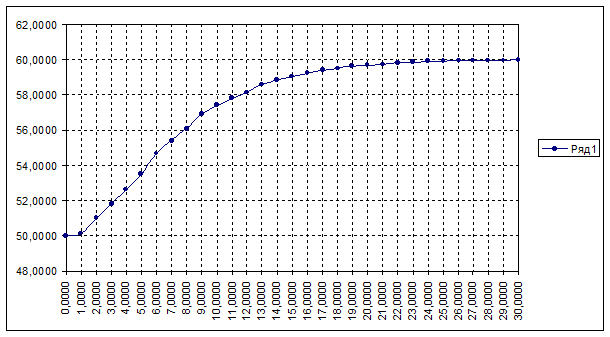
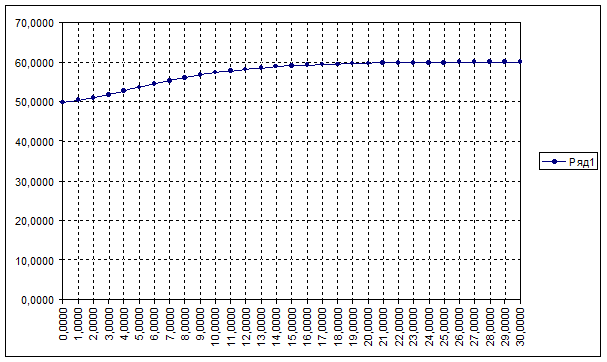
Координаты и график кривой разгона по заданию.
| 1 | 0,0000 | 50,0000 |
| 2 | 1,0000 | 50,1500 |
| 3 | 2,0000 | 51,0000 |
| 4 | 3,0000 | 51,8000 |
| 5 | 4,0000 | 52,6500 |
| 6 | 5,0000 | 53,5000 |
| 7 | 6,0000 | 54,7000 |
| 8 | 7,0000 | 55,4000 |
| 9 | 8,0000 | 56,1000 |
| 10 | 9,0000 | 56,9000 |
| 11 | 10,0000 | 57,4000 |
| 12 | 11,0000 | 57,8000 |
| 13 | 12,0000 | 58,1500 |
| 14 | 13,0000 | 58,6000 |
| 15 | 14,0000 | 58,8500 |
| 16 | 15,0000 | 59,0500 |
| 17 | 16,0000 | 59,2500 |
| 18 | 17,0000 | 59,4000 |
| 19 | 18,0000 | 59,5000 |
| 20 | 19,0000 | 59,6500 |
| 21 | 20,0000 | 59,7000 |
| 22 | 21,0000 | 59,7500 |
| 23 | 22,0000 | 59,8000 |
| 24 | 23,0000 | 59,8500 |
| 25 | 24,0000 | 59,9000 |
| 26 | 25,0000 | 59,9000 |
| 27 | 26,0000 | 59,9500 |
| 28 | 27,0000 | 59,9500 |
| 29 | 28,0000 | 59,9500 |
| 30 | 29,0000 | 59,9500 |
| 31 | 30,0000 | 60,0000 |
|
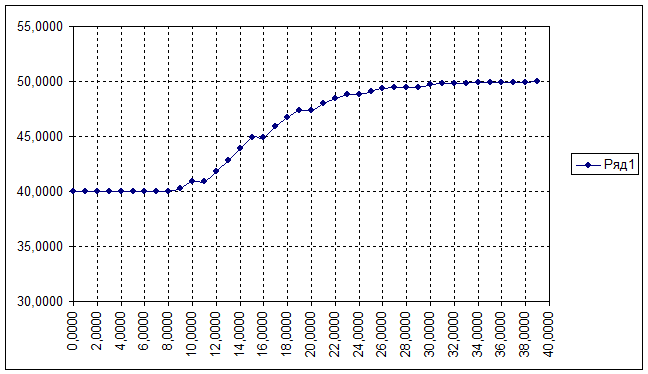
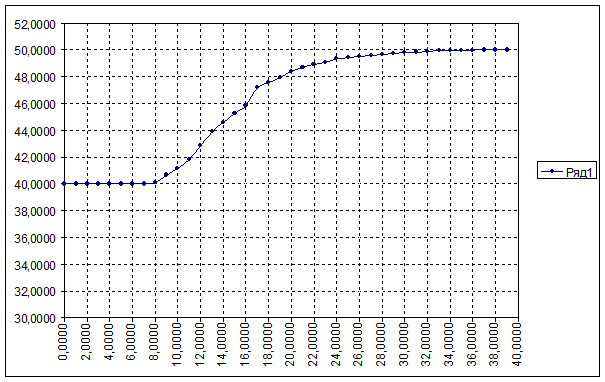
Координаты и график кривой разгона по управлению.
| 1 | 0,0000 | 40,0000 | 21 | 20,0000 | 47,4000 |
| 2 | 1,0000 | 40,0000 | 22 | 21,0000 | 48,0000 |
| 3 | 2,0000 | 40,0000 | 23 | 22,0000 | 48,4500 |
| 4 | 3,0000 | 40,0000 | 24 | 23,0000 | 48,8000 |
| 5 | 4,0000 | 40,0000 | 25 | 24,0000 | 48,8000 |
| 6 | 5,0000 | 40,0000 | 26 | 25,0000 | 49,1000 |
| 7 | 6,0000 | 40,0000 | 27 | 26,0000 | 49,3500 |
| 8 | 7,0000 | 40,0000 | 28 | 27,0000 | 49,5000 |
| 9 | 8,0000 | 40,0000 | 29 | 28,0000 | 49,5000 |
| 10 | 9,0000 | 40,2500 | 30 | 29,0000 | 49,5000 |
| 11 | 10,0000 | 40,9000 | 31 | 30,0000 | 49,7000 |
| 12 | 11,0000 | 40,9000 | 32 | 31,0000 | 49,8000 |
| 13 | 12,0000 | 41,8000 | 33 | 32,0000 | 49,8000 |
| 14 | 13,0000 | 42,8500 | 34 | 33,0000 | 49,8500 |
| 15 | 14,0000 | 43,9500 | 35 | 34,0000 | 49,9000 |
| 16 | 15,0000 | 44,9500 | 36 | 35,0000 | 49,9500 |
| 17 | 16,0000 | 44,9500 | 37 | 36,0000 | 49,9500 |
| 18 | 17,0000 | 45,9000 | 38 | 37,0000 | 49,9500 |
| 19 | 18,0000 | 46,7500 | 39 | 38,0000 | 49,9500 |
| 20 | 19,0000 | 47,4000 | 40 | 39,0000 | 50,0000 |
|
Интерполяция по трем точкам.
В программе ASR, пользуясь пунктом “интерполировать по 3-м” поочередно считаем кривые разгона и строим соответствующий график.
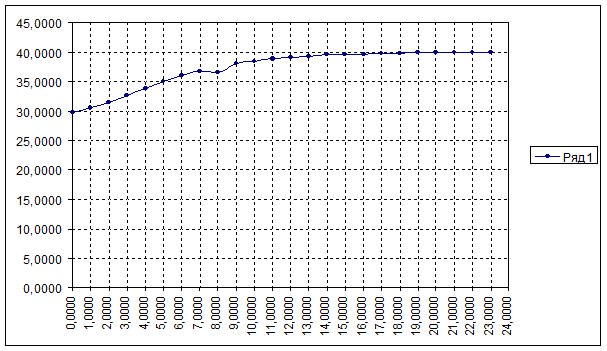
Линейное сглаживание и график кривой разгона по возмущению.
| 1 | 0,0000 | 29,8167 | ||
| 2 | 1,0000 | 30,5667 | ||
| 3 | 2,0000 | 31,4333 | ||
| 4 | 3,0000 | 32,6000 | ||
| 5 | 4,0000 | 33,8500 | ||
| 6 | 5,0000 | 35,0167 | ||
| 7 | 6,0000 | 36,0667 | ||
| 8 | 7,0000 | 36,8000 | ||
| 9 | 8,0000 | 36,5000 | ||
| 10 | 9,0000 | 38,0667 | ||
| 11 | 10,0000 | 38,5333 | ||
| 12 | 11,0000 | 38,8667 | ||
| 13 | 12,0000 | 39,1500 | ||
| 14 | 13,0000 | 39,3833 | ||
| 15 | 14,0000 | 39,5333 | ||
| 16 | 15,0000 | 39,6500 | ||
| 17 | 16,0000 | 39,7333 | ||
| 18 | 17,0000 | 39,8000 | ||
| 19 | 18,0000 | 39,8500 | ||
| 20 | 19,0000 | 39,9000 | ||
| 21 | 20,0000 | 39,9333 | ||
| 22 | 21,0000 | 39,9500 | ||
| 23 | 22,0000 | 39,9667 | ||
|
23,0000 | 39,9917 |
Линейное сглаживание и график кривой разгона по заданию.
| 1 | 0,0000 | 49,8833 |
| 2 | 1,0000 | 50,3833 |
| 3 | 2,0000 | 50,9833 |
| 4 | 3,0000 | 51,8167 |
| 5 | 4,0000 | 52,6500 |
| 6 | 5,0000 | 53,6167 |
| 7 | 6,0000 | 54,5333 |
| 8 | 7,0000 | 55,4000 |
| 9 | 8,0000 | 56,1333 |
| 10 | 9,0000 | 56,8000 |
| 11 | 10,0000 | 57,3667 |
| 12 | 11,0000 | 57,7833 |
| 13 | 12,0000 | 58,1833 |
| 14 | 13,0000 | 58,5333 |
| 15 | 14,0000 | 58,8333 |
| 16 | 15,0000 | 59,0500 |
| 17 | 16,0000 | 59,2333 |
| 18 | 17,0000 | 59,3833 |
| 19 | 18,0000 | 59,5167 |
| 20 | 19,0000 | 59,6167 |
| 21 | 20,0000 | 59,7000 |
| 22 | 21,0000 | 59,7500 |
| 23 | 22,0000 | 59,8000 |
| 24 | 23,0000 | 59,8500 |
| 25 | 24,0000 | 59,8833 |
| 26 | 25,0000 | 59,9167 |
| 27 | 26,0000 | 59,9333 |
| 28 | 27,0000 | 59,9500 |
| 29 | 28,0000 | 59,9667 |
| 30 | 29,0000 | 59,9833 |
| 31 | 30,0000 | 59,9833 |
|
Линейное сглаживание и график кривой разгона по управлению.
| 1 | 0,0000 | 40,0000 | 21 | 20,0000 | 48,4167 |
| 2 | 1,0000 | 40,0000 | 22 | 21,0000 | 48,6833 |
| 3 | 2,0000 | 40,0000 | 23 | 22,0000 | 48,9000 |
| 4 | 3,0000 | 40,0000 | 24 | 23,0000 | 49,0833 |
| 5 | 4,0000 | 40,0000 | 25 | 24,0000 | 49,3167 |
| 6 | 5,0000 | 40,0000 | 26 | 25,0000 | 49,4500 |
| 7 | 6,0000 | 40,0000 | 27 | 26,0000 | 49,5333 |
| 8 | 7,0000 | 40,0000 | 28 | 27,0000 | 49,6000 |
| 9 | 8,0000 | 40,0833 | 29 | 28,0000 | 49,7000 |
| 10 | 9,0000 | 40,6833 | 30 | 29,0000 | 49,7667 |
| 11 | 10,0000 | 41,2000 | 31 | 30,0000 | 49,8167 |
| 12 | 11,0000 | 41,8500 | 32 | 31,0000 | 49,8500 |
| 13 | 12,0000 | 42,8667 | 33 | 32,0000 | 49,9000 |
| 14 | 13,0000 | 43,9167 | 34 | 33,0000 | 49,9333 |
| 15 | 14,0000 | 44,6167 | 35 | 34,0000 | 49,9500 |
| 16 | 15,0000 | 45,2667 | 36 | 35,0000 | 49,9500 |
| 17 | 16,0000 | 45,8667 | 37 | 36,0000 | 49,9667 |
| 18 | 17,0000 | 47,1833 | 38 | 37,0000 | 49,9917 |
| 19 | 18,0000 | 47,6000 | 39 | 38,0000 | 49,9917 |
| 20 | 19,0000 | 47,9500 | 40 | 39,0000 | 50,0000 |
|
Нормирование кривых разгона.
С помощью программы ASR в пункте нормировать последовательно производим нормирование сглаженных кривых и упорядочиваем время начиная с 0,0000, с шагом 1.0
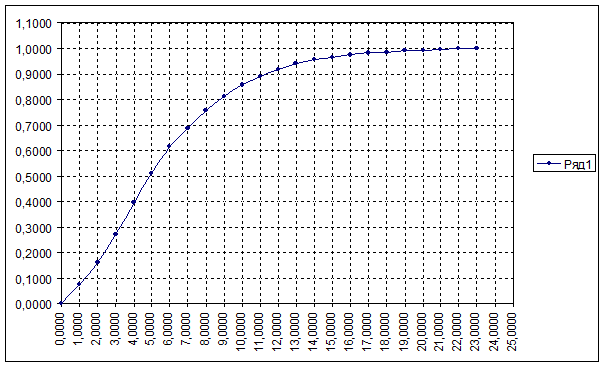
Нормированная кривая разгона по возмущению.
| 1 | 0,0000 | 0,0000 | ||
| 2 | 1,0000 | 0,0737 | ||
| 3 | 2,0000 | 0,1589 | ||
| 4 | 3,0000 | 0,2735 | ||
| 5 | 4,0000 | 0,3964 | ||
| 6 | 5,0000 | 0,5111 | ||
| 7 | 6,0000 | 0,6143 | ||
| 8 | 7,0000 | 0,6863 | ||
| 9 | 8,0000 | 0,7551 | ||
| 10 | 9,0000 | 0,8108 | ||
| 11 | 10,0000 | 0,8567 | ||
| 12 | 11,0000 | 0,8894 | ||
| 13 | 12,0000 | 0,9173 | ||
| 14 | 13,0000 | 0,9402 | ||
| 15 | 14,0000 | 0,9550 | ||
| 16 | 15,0000 | 0,9664 | ||
| 17 | 16,0000 | 0,9746 | ||
| 18 | 17,0000 | 0,9812 | ||
| 19 | 18,0000 | 0,9861 | ||
| 20 | 19,0000 | 0,9910 | ||
| 21 | 20,0000 | 0,9943 | ||
| 22 | 21,0000 | 0,9959 | ||
| 23 | 22,0000 | 0,9975 | ||
|
23,0000 | 1,0000 |
Нормированная кривая разгона по заданию.
| 1 | 0,0000 | 0,0000 | ||
| 2 | 1,0000 | 0,0494 | ||
| 3 | 2,0000 | 0,1086 | ||
| 4 | 3,0000 | 0,1909 | ||
| 5 | 4,0000 | 0,2733 | ||
| 6 | 5,0000 | 0,3687 | ||
| 7 | 6,0000 | 0,4593 | ||
| 8 | 7,0000 | 0,5449 | ||
| 9 | 8,0000 | 0,6173 | ||
| 10 | 9,0000 | 0,6831 | ||
| 11 | 10,0000 | 0,7391 | ||
| 12 | 11,0000 | 0,7802 | ||
| 13 | 12,0000 | 0,8198 | ||
| 14 | 13,0000 | 0,8543 | ||
| 15 | 14,0000 | 0,8840 | ||
| 16 | 15,0000 | 0,9053 | ||
| 17 | 16,0000 | 0,9235 | ||
| 18 | 17,0000 | 0,9383 | ||
| 19 | 18,0000 | 0,9514 | ||
| 20 | 19,0000 | 0,9613 | ||
| 21 | 20,0000 | 0,9745 | ||
| 22 | 21,0000 | 0,9794 | ||
| 23 | 22,0000 | 0,9909 | ||
| 24 | 23,0000 | 0,9926 | ||
| 25 | 24,0000 | 0,9942 | ||
| 26 | 25,0000 | 0,9942 | ||
| 27 | 26,0000 | 0,9975 | ||
|
27,0000 | 1,0000 |
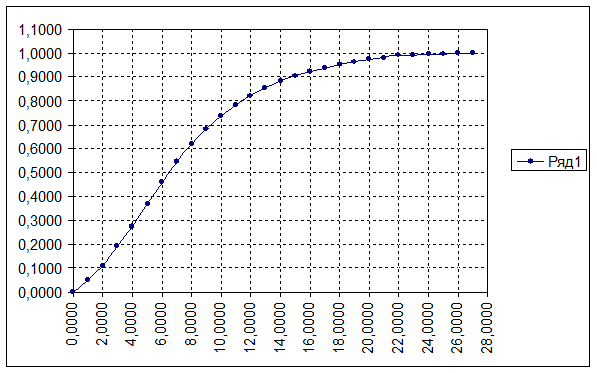
Нормированная кривая разгона по управлению.
| 1 | 0,0000 | 0,0000 | 21 | 20,0000 | 0,7606 |
| 2 | 1,0000 | 0,0000 | 22 | 21,0000 | 0,7957 |
| 3 | 2,0000 | 0,0000 | 23 | 22,0000 | 0,8424 |
| 4 | 3,0000 | 0,0000 | 24 | 23,0000 | 0,8691 |
| 5 | 4,0000 | 0,0000 | 25 | 24,0000 | 0,8907 |
| 6 | 5,0000 | 0,0000 | 26 | 25,0000 | 0,9091 |
| 7 | 6,0000 | 0,0000 | 27 | 26,0000 | 0,9324 |
| 8 | 7,0000 | 0,0000 | 28 | 27,0000 | 0,9458 |
| 9 | 8,0000 | 0,0083 | 29 | 28,0000 | 0,9541 |
| 10 | 9,0000 | 0,0384 | 30 | 29,0000 | 0,9608 |
| 11 | 10,0000 | 0,0684 | 31 | 30,0000 | 0,9708 |
| 12 | 11,0000 | 0,1201 | 32 | 31,0000 | 0,9775 |
| 13 | 12,0000 | 0,1852 | 33 | 32,0000 | 0,9825 |
| 14 | 13,0000 | 0,2869 | 34 | 33,0000 | 0,9858 |
| 15 | 14,0000 | 0,3920 | 35 | 34,0000 | 0,9908 |
| 16 | 15,0000 | 0,4621 | 36 | 35,0000 | 0,9942 |
| 17 | 16,0000 | 0,5271 | 37 | 36,0000 | 0,9958 |
| 18 | 17,0000 | 0,5872 | 38 | 37,0000 | 0,9958 |
| 19 | 18,0000 | 0,6689 | 39 | 38,0000 | 0,9975 |
| 20 | 19,0000 | 0,7189 | 40 | 39,0000 | 1,0000 |
|
Аппроксимация методом Симою.
С помощью программы ASR в пункту аппроксимации последовательно считаем площади каждой из кривой разгона для последующего получения уравнения передаточной функции.
Для кривой разгона по возмущению для объекта второго порядка получаем следующие данные:
Значения коэффициентов:
F1= 6.5614
F2= 11.4658
F3= -4.5969
F4= -1.1636
F5= 44.0285
F6= -120.0300
Ограничимся второй площадью. F1>F2, тогда передаточная функция по возмущению для объекта второго порядка имеет вид:
1
W(s)=---------------------------
2
11,4658s + 6.5614s + 1
Для кривой разгона по заданию для объекта второго порядка получаем следующие данные:
Значения коэффициентов:
F1= 9.5539
F2= 24.2986
F3= -16.7348
F4= -14.7318
F5= 329.7583
F6= -1179.3989
Ограничимся второй площадью , с учетом того что F1>F2. Тогда передаточная функция по управлению для объекта второго порядка имеет вид:
1
W(s)=----------------------------
2
24,2986s + 9.5539s +1
Для кривой разгона по заданию для объекта третьего порядка с запаздыванием получаем следующие данные:
Значения коэффициентов:
F1= 10.6679
F2= 38.1160
F3= 30.4228
F4= -46.5445
F5= 168.8606
F6= -33.3020
Ограничимся третьей площадью и учтем что каждая последующая площадь больше предыдущей. Тогда передаточная функция по заданию для объекта третьего порядка с запаздыванием имеет вид:
1
W(s)=----------------------------------------
3 2
30,4228s + 38.1160s + 10.7769 + 1
Проверка аппроксимации методом Рунге - Кутта.
В программе ASR в пункте передаточная функция задаем полученные передаточные функции. И затем строим графики экспериментальной и аналитической кривых разгона (по полученной передаточной функции).
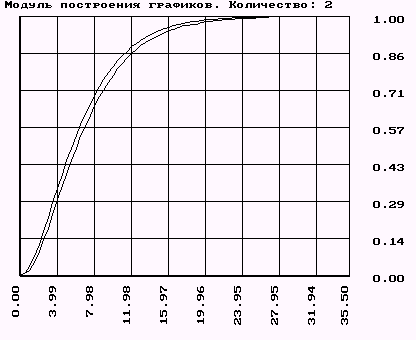
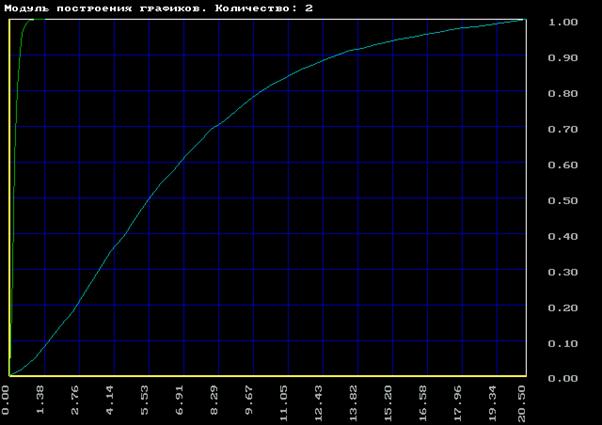
Для кривой разгона по возмущению.
Устанавливаем для проверки методом Рунге-Кутта конечное время 35,5с, шаг 0,5с.
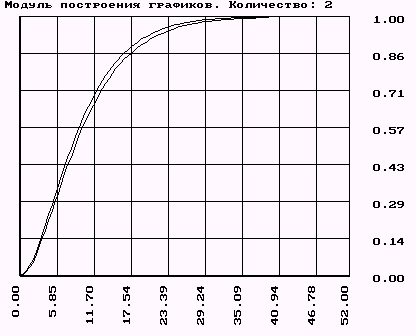
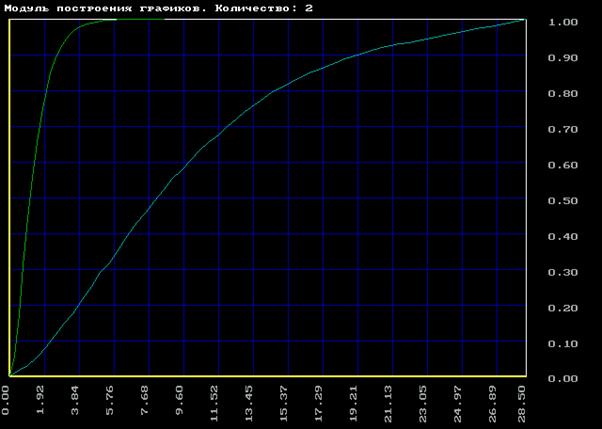
Для кривой разгона по заданию.
Устанавливаем конечное время 55с, шаг 0,5с.
Для кривой разгона по управлению.
При задании передаточной функции учитываем чистое запаздывание 0,08с.
Устанавливаем конечное время 39с, шаг изменения 0,5с.
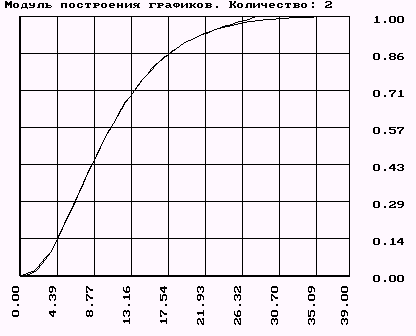
Получили, что кривые разгона практически одинаковы, следовательно аппроксимация методом Симою сделана верно.
Для объекта второго порядка по возмущению имеем погрешность метода около 25%, по заданию - около 15%, а для объекта третьего порядка с запаздыванием по управлению - около 5%.
Сравним экспериментальные и исходные передаточные функции:
 |
объект исходная экспериментальная
передаточная передаточная
функция функция
 |
второго порядка 1 1
по возмущению W(s)= -------------------- W(s)= -----------------------------
2 2
0.01s + 0.2s + 1 11.465s + 6.5614s +1
 |
второго порядка 1 1
по заданию W(s)= ----------------------- W(s)= -----------------------------
2 2
0.4489s + 1.34s +1 24.2986s + 9.5539s +1
 |
третьего порядка 1000 1
с запаздыванием W(s)= ------------------------------------- W(s)= -------------------------------------
по управлению 3 2 3 2
4.2188s + 168.75s + 2250s + 1 30.4228s + 38.116s + 10.7769s + 1
Полученные значению передаточных функций отличают на 1000 - 7500, что говорит о достаточно большой погрешности между фактическими и экспериментальными данными.
Для исходных передаточных функций с помощью программы ASR, пунктов аппроксимация (создать передаточную функцию и изменить время) получим координаты кривых разгона и сравним их с экспериментальной кривой:
1. по возмущению:
| 0,0000 | 0,0000 |
| 0,1000 | 0,2917 |
| 0,2000 | 0,6094 |
| 0,3000 | 0,8066 |
| 0,4000 | 0,9099 |
| 0,5000 | 0,9596 |
| 0,6000 | 0,9824 |
| 0,7000 | 0,9925 |
| 0,8000 | 0,9968 |
| 0,9000 | 0,9987 |
| 1,0000 | 0,9995 |
| 1,1000 | 0,9998 |
| 1,2000 | 0,9999 |
| 1,3000 | 1,0000 |
2. по заданию:
| 1 | 0,0000 | 0,0000 | 17 | 4,0000 | 0,9822 |
| 2 | 0,2500 | 0,0547 | 18 | 4,2500 | 0,9871 |
| 3 | 0,5000 | 0,1723 | 19 | 4,5000 | 0,9907 |
| 4 | 0,7500 | 0,3083 | 20 | 4,7500 | 0,9933 |
| 5 | 1,0000 | 0,4399 | 21 | 5,0000 | 0,9951 |
| 6 | 1,2500 | 0,5565 | 22 | 5,2500 | 0,9965 |
| 7 | 1,5000 | 0,6549 | 23 | 5,5000 | 0,9975 |
| 8 | 1,7500 | 0,7350 | 24 | 5,7500 | 0,9982 |
| 9 | 2,0000 | 0,7987 | 25 | 6,0000 | 0,9987 |
| 10 | 2,2500 | 0,8484 | 26 | 6,2500 | 0,9991 |
| 11 | 2,5000 | 0,8867 | 27 | 6,5000 | 0,9993 |
| 12 | 2,7500 | 0,9158 | 28 | 6,7500 | 0,9995 |
| 13 | 3,0000 | 0,9378 | 29 | 7,0000 | 0,9997 |
| 14 | 3,2500 | 0,9542 | 30 | 7,2500 | 0,9998 |
| 15 | 3,5000 | 0,9665 | 31 | 7,5000 | 0,9999 |
| 16 | 3,7500 | 0,9755 | 32 | 7,7500 | 1,0000 |
3. по управлению:
Сравнивая экспериментальные и фактические кривые разгона видим, что они отличаются очень сильно. Фактическая кривая разгона приходит к 1 на много быстрее, чем экспериментальная.
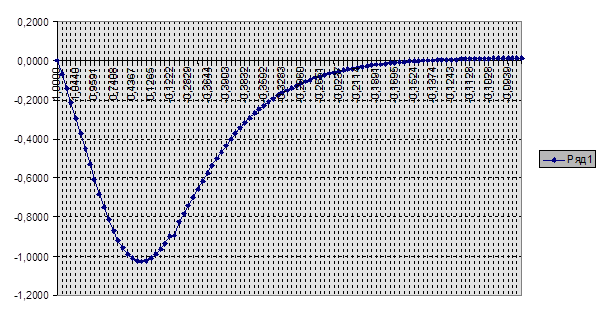
Расчет АФХ передаточных функций.
1. Объект второго порядка по возмущению:
а) экспериментальная:
| 1 | 1,0000 | 0,0000 | 34 | -0,3751 | -0,5372 | 68 | -0,1944 | -0,0241 |
| 2 | 1,0211 | -0,0678 | 35 | -0,3828 | -0,5004 | 69 | -0,1891 | -0,0210 |
| 3 | 1,0360 | -0,1397 | 36 | -0,3877 | -0,4653 | 70 | -0,1839 | -0,0182 |
| 4 | 1,0438 | -0,2150 | 37 | -0,3903 | -0,4320 | 71 | -0,1790 | -0,0155 |
| 5 | 1,0440 | -0,2927 | 38 | -0,3909 | -0,4006 | 72 | -0,1741 | -0,0131 |
| 6 | 1,0359 | -0,3720 | 39 | -0,3897 | -0,3709 | 73 | -0,1695 | -0,0108 |
| 7 | 1,0191 | -0,4516 | 40 | -0,3871 | -0,3431 | 74 | -0,1650 | -0,0087 |
| 8 | 0,9935 | -0,5304 | 41 | -0,3832 | -0,3170 | 75 | -0,1606 | -0,0067 |
| 9 | 0,9591 | -0,6072 | 42 | -0,3783 | -0,2927 | 76 | -0,1564 | -0,0049 |
| 10 | 0,9161 | -0,6805 | 43 | -0,3725 | -0,2699 | 77 | -0,1524 | -0,0032 |
| 11 | 0,8649 | -0,7492 | 44 | -0,3661 | -0,2488 | 78 | -0,1484 | -0,0017 |
| 12 | 0,8062 | -0,8121 | 45 | -0,3592 | -0,2291 | 79 | -0,1446 | -0,0003 |
| 13 | 0,7408 | -0,8681 | 46 | -0,3518 | -0,2108 | 80 | -0,1410 | 0,0011 |
| 14 | 0,6700 | -0,9163 | 47 | -0,3442 | -0,1939 | 81 | -0,1374 | 0,0023 |
| 15 | 0,5948 | -0,9560 | 48 | -0,3363 | -0,1781 | 82 | -0,1340 | 0,0034 |
| 16 | 0,5166 | -0,9868 | 49 | -0,3283 | -0,1636 | 83 | -0,1306 | 0,0045 |
| 17 | 0,4367 | -1,0085 | 50 | -0,3202 | -0,1501 | 84 | -0,1274 | 0,0055 |
| 18 | 0,3565 | -1,0211 | 51 | -0,3121 | -0,1376 | 85 | -0,1243 | 0,0064 |
| 19 | 0,2774 | -1,0249 | 52 | -0,3040 | -0,1260 | 86 | -0,1213 | 0,0072 |
| 20 | 0,2003 | -1,0203 | 53 | -0,2960 | -0,1153 | 87 | -0,1184 | 0,0079 |
| 21 | 0,1265 | -1,0081 | 54 | -0,2880 | -0,1054 | 88 | -0,1156 | 0,0086 |
| 22 | 0,0567 | -0,9890 | 55 | -0,2802 | -0,0962 | 89 | -0,1128 | 0,0093 |
| 23 | -0,0083 | -0,9640 | 56 | -0,2726 | -0,0877 | 90 | -0,1102 | 0,0099 |
| 24 | -0,0680 | -0,9339 | 57 | -0,2651 | -0,0799 | 91 | -0,1076 | 0,0104 |
| 25 | -0,1222 | -0,8997 | 58 | -0,2577 | -0,0726 | 92 | -0,1052 | 0,0109 |
| 26 | -0,1708 | -0,8924 | 59 | -0,2505 | -0,0659 | 93 | -0,1028 | 0,0114 |
| 27 | -0,2136 | -0,8228 | 60 | -0,2435 | -0,0597 | 94 | -0,1004 | 0,0118 |
| 28 | -0,2509 | -0,7817 | 61 | -0,0237 | -0,0540 | 95 | -0,0982 | 0,0122 |
| 29 | -0,2829 | -0,7399 | 62 | -0,2301 | -0,0487 | 96 | -0,0960 | 0,0126 |
| 30 | -0,3098 | -0,6978 | 63 | -0,2237 | -0,0437 | 97 | -0,0939 | 0,0129 |
| 31 | -0,3322 | -0,6562 | 64 | -0,2175 | -0,0392 | 98 | -0,0918 | 0,0132 |
| 32 | -0,3502 | -0,6153 | 65 | -0,2114 | -0,0350 | 99 | -0,0898 | 0,0134 |
| 33 | -0,3644 | -0,5756 | 66 | -0,2056 | -0,0311 | 100 | -0,0879 | 0,0134 |
| 67 | -0,1999 | -0,0275 |
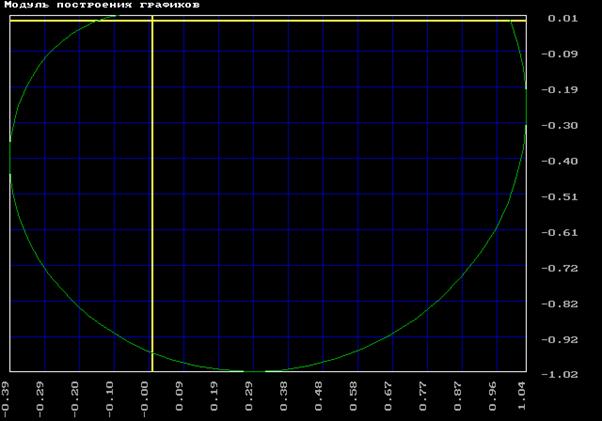
б) фактическая
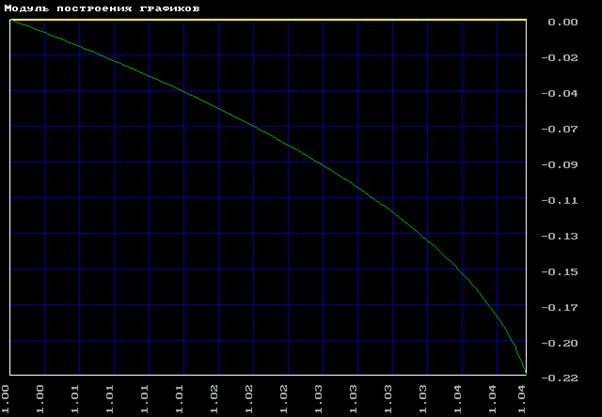2. Объект второго порядка по заданию.
а) экспериментальная
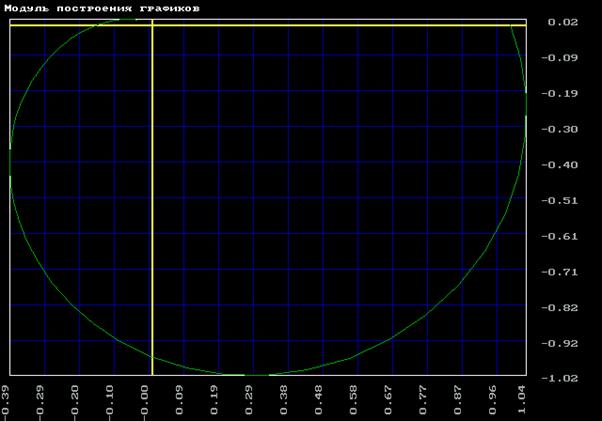
б) фактическая
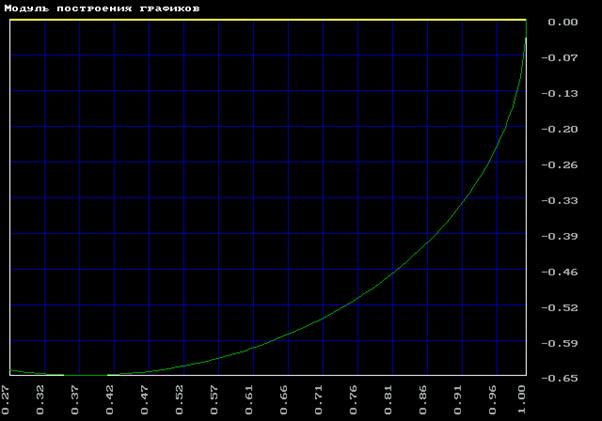
3. Объект третьего порядка с запаздыванием по управлению
а) экспериментальная
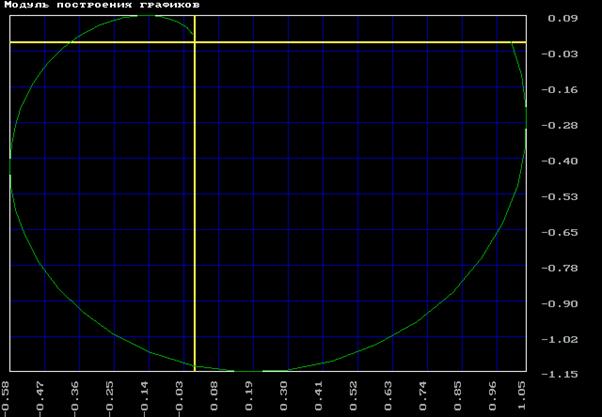
б) фактическая
Расчет одноконтурной АСР методом Роточа.
В программе Linreg задаем параметры объекта с учетом оператора Лапласса.