Реферат: Загальні уявлення про індуктивні фільтри

Лекція

Загальн і уявлення про індуктивні фільтри

Зміст

Вступ

1. Фільтри верхніх частот (ФВЧ)

2. Смугові фільтри та інші типи індукційних фільтрів

3. Вплив навантаження на характеристики фільтрів

Висновок

Вступ

В даній лекції будуть розглянуті фізичні процеси у фільтрах верхніх частот, смугових, загороджувальних, режекторних. Ці фільтри як і фільтри нижніх частот широко використовуються в апаратурі радіозв’язку, радіорелейному зв’язку, а особливо в системах передачі з частотним розділом каналів.

Учбово-виховні ціл і: Вивчити принципи побудови фільтрів верхніх частот, смугових та режекторних фільтрів, області їх використання; Виховати високу культуру інженера-зв’язківця.

Учбово-матеріальне забезпечення : Принципіальні схеми апаратури, її функціональні вузли з ФВЧ та СФ\П-303\, Діапроектор, діапозитиви.

Виявляється, що використовуючи так званий метод перетворення частоти, можна при розрахунках фільтрів верхніх частот та інших фільтрів використати всі методи, формули, малограми та таблиці, одержані для фільтрів нижніх частот.

У вступі акцентувати увагу курсантів на важливість теми вивчення, використовуючи схеми та блоки реальної апаратури зв’язку. Показати широке застосування різних видів фільтрів.

У першому питанні коротко викласти суть методу частотної змінної та на його основі дати алгоритм одержання фільтрів верхніх частот з фільтрів нижніх частот.

У другому питанні теж, використовуючи метод частотної змінної, показати принцип одержання смугових фільтрів, загороджувальних, режекторних фільтрів з ФНЧ прототипів.

У третьому питанні показати, як змінюються параметри та характеристики фільтрів при підключення до них навантаження та зміни її другої величини.

В заключній частині узагальнити матеріал і ще раз акцентувати увагу на вузлових моментах теми.

1. Фільтри верхніх частот (фвч)

При розгляданні принципів побудови фільтрів верхніх частот почнемо з розгляду сутності методу перетворення частотної змінної.

Практично всі фільтри верхніх частот можна одержати з фільтрів нижніх частот, якщо в останніх кожну індуктивність замінити ємністю, а кожну ємність – індуктивністю. (мал.1)

мал. 1 а ). б ). в ).

Затухання ФНЧ виражається співвідношенням дб., тобто є парною функцією частоти , з цього слідує – крива затухання буде симетрична відносно осі ординат (мал. 2)

мал. 2

Ліва частина цього графіку відповідає взаємному розміщенню смуги затримки та смуги пропускання для фільтрів верхніх частот. (мал. 3)

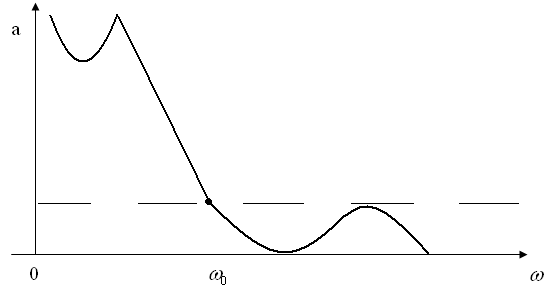
мал. 3

Підберемо таку функцію, яка б перетворила від’ємну піввісь (мал.2) в додатну (мал. 3) піввісь.

При цьому точці (мал. 2) повинна відповідати точка “0” (мал. 3)

"-1" ""

"0" ""

Очевидно, що такою функцією буде така:

(1)

Таким чином, всі вирази, одержані раніш для фільтрів нижніх частот, будуть вірні і для фільтрів верхніх частот, якщо в цих виразах визначатиметься із співвідношення (1).

Нормуванні по частоті дозволяє при розрахунках фільтрів верхніх частот з характеристиками Баттерворта, Чебишева, Золотарьова або з довільним розміщенням сплесків затухання повністю використовувати всі методи, формули, номограми та таблиці, одержані для фільтрів верхніх частот. В якості прикладу на (мал. 4) наведені схеми та характеристики деяких фільтрів верхніх частот з рівнохвильовими характеристиками затухання, а на (мал. 5) схема фільтра к -2,0 апаратури П-303 та графік частотної залежності робочого затухання цього фільтру.

мал. 4

мал. 5

2. Смугові фільтри та інші типи індукційних фільтрів

Смуговий фільтр може бути утворений з фільтру нижніх частот, якщо в останньому кожну індуктивність замінити послідовним коливальним контуром без втрат, а кожну ємність – паралельним, при чому резонансні частоти всіх контурів взяти однаковими (мал. 6)

ФНЧСФ

мал.6

Тоді до частоти резонансу характер опору віток, одержаного фільтра, буде таким самим як і у фільтра верхніх частот, а після частоти резонансу – таким самим як у фільтра нижніх частот. Фільтр же в цілому буде смуговим фільтром, при ому частота резонансних контурів буде очевидно знаходитись у смузі пропускання фільтру.

Підберемо таку функцію яка б перетворила вісь частот () (мал. 2) у піввісь () (мал. 7)

мал. 7

При цьому:

Точці "-" (мал. 2) повинна відповідати точка "0" (мал. 7).

"-1" ""

"0" ""

"1" ""

"" ""

Таке перетворення може зробити функція:

(2)

Таким чином, всі вирази, одержані раніш для фільтрів нижніх частот, залишаються справедливими і для розглядуваних смугових фільтрів, якщо в цих виразах визначати з відношення (2).

Важливо відмітити, що частотні характеристики розглянутих фільтрів володіють однією характерною особливістю, яка обумовлена тим, що функція (2) приймає рівні по абсолютній величині і обернені за знаком значення для будь-якої пари частот та зв’язаних співвідношенням , тобто для будь-якої пари частот, розміщених симетрично відносно осі части , яка в свою чергу являється середньою геометричною частотою смуги пропускання фільтра.

Отже затухання фільтра при частотах та 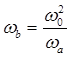буде однаковим, тобто характеристика затухання будь-якого речового фільтра, одержаного з допомогою перетворення (2) завжди буде геометрично симетрична відносно частоти відповідає графічна ілюстрація на (мал. 7)

Тому подібні фігури одержали назви фільтрів з симетричними (геометричними) характеристиками загасання.

Практичне використання фільтрів, розглянутих вище, обмежено лише тими випадками, коли вимоги до характеристики затухання фільтра по обидві сторони від його смуги пропускання близькі до симетричних. В іншому випадку в деяких частотних областях буде мати місце невиправданий великий запас затухання, що говорить про існування більш економічного рішення по числу елементів. У відповідності з цим в загальному випадку смуговий фільтр може мати різне число сплесків зліва і справа від йог смуги пропускання, різну крутизну характеристики затухання при та при , що різко відрізняються по широті смуги переходу, коротшу характеристику затухання, яка суттєво відрізняється від симетричної.

Одна й та сама передаточна функція смугового фільтру може бути реалізована тим більшим числом, зовнішньо розрізняючих ступінчатих реактивних чотирьохполюсників, чим вище порядок функції. Частіше інших знаходять застосування фільтри, схеми яких подібні до схем фільтрів з симетричними характеристиками, схеми у вигляді каскадного з’єднання фільтра нижніх і верхніх частот. Крім ФНЧ, ФВЧ, СФ в техніці часто використовуються режекторні або, як їх іще називають, загороджувальні фільтри.

Характеристика загороджувального фільтра має вигляд, зображений на (мал. 8)

мал. 8

Якщо зрівняти цю характеристику смугового фільтра, то можна побачити, загороджувальний фільтр має характеристику затухання обернену до характеристики СФ, отже він також може бути одержаний з ФНЧ – прототипу, однак в цьому випадку в ФНЧ кожну ємність замінити послідовним коливальним контуром, а індуктивність – паралельним (мал. 9) причому резонансна частота всіх контурів повинна бути однаковою, тоді очевидно, що такий фільтр буде вільно (з малим затуханням) пропускати всі частоти нижчі і вище резонансної частоти контурів, а на частотах близьких до резонансу затухання фільтру буде великим, так як послідовні контури будуть надавати штучну дію на вхідний сигнал, а паралельний контур буде мати для нього великий опір.

ФНЧ СФ \ ЗФ

мал. 9

У радіолокаційній техніці широко використовується гребінчасті фільтри, у яких смуги пропускання чергуються зі смугами затримки. Е багато способів одержання гребінчастої характеристики затухання. Найпростішим з них є спосіб утворення такої характеристики з допомогою набору смугових або режекторних фільтрів. На (мал. 10(а,б) ) зображений спосіб отримання гребінчастої характеристики затухання.

вих

мал. 10 а.

вх.

вих.

мал. 10 б.

3. Вплив навантаження на характеристики фільтрів

Вплив опору навантаження на характеристики фільтрів розглянемо на прикладі найпростішого ФНЧ. Коли фільтр навантажений на опір z_н =z₀ , тобто не характеристичне, такий режим називається режимом узгодження.

мал. 11

В цьому випадку характеристика фільтра буде мати вигляд, показаний на мал. 12

мал. 12

Необхідно підкреслити, що такий вид характеристики фільтр буде мати лише тоді, коли він буде навантажений на опір, рівний характеристичному. Щоб вияснити можливе існування такого режиму, необхідно знайти характеристичний опір даного фільтра.

мал. 13

Користуючись теорією чотирьохполюсників можна написати для П-подібної схеми фільтра формулу, яка виражає залежність характеристичного опору від частоти

,

де - хвильовий опір. Графік цієї залежності представлений на мал. 13.

мал. 14

Як видно з мал. 13 опір сильно залежить від частоти як по характеру так і по величині. Це характерно для будь-якої схеми фільтру. Отже, бажаючи здійснити узгодження навантаження, потрібно було б для кожної частоти підбирати свій опір навантаження \в смузі пропускання – активне, в смузі затримки - реактивне. Між тим, в дійсних умовах роботи опору навантаження, як правило, являється практично не залежним від частоти активного опору R_н . Звідси слідує, що в загальному випадку фільтр працює на неузгоджене навантаження, і до режиму узгодження можна лише наблизитись.

Користуючись тією ж теорією чотирьохполюсників можна визначити залежність затухання фільтру від опору навантаження.

При холостому ході фільтру R_н = в смузі пропускання затухання стає від’ємним, тобто коефіцієнт передачі фільтра більше одиниці. Це означає підсилення сигналу по потужності так як фільтр є пасивним.

В загалі ж в реальних умовах частотні характеристики фільтра відрізняються від тих, які були б при умові повного узгодження.

Висновок

Таким чином в даній лекції розглянуті фізичні процеси та принципи побудови фільтрів верхніх частот, смугових та режекторних.

Використовуючи принципи перетворення частоти, ми впевнилися, що всі вирази, одержані раніше для фільтрів нижніх частот, виявляються вірними і для фільтрів верхніх частот, якщо в цих виразах визначати з виразу (1) . Взагалі фільтр верхніх частот може бути утворений з фільтру нижніх частот, якщо у ньому кожну індуктивність замінити на ємністю, а кожну ємність – індуктивністю.

Всі вирази, одержані раніше для фільтрів нижніх частот, залишаються вірними і для смугових фільтрів, якщо в цих виразах визначити із співвідношення (2).

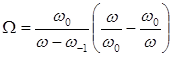
Смуговий фільтр може бути утворений з фільтра нижніх частот, якщо в ньому кожну індуктивність замінити послідовним коливальним контуром, а кожну ємність – паралельним.

Режекторний фільтр може бути утворений з ФНЧ – прототипу, якщо в ньому кожну індуктивність замінити паралельним коливальним контуром, а кожну ємність послідовним.

Для забезпечення активної роботи фільтра він повинен бути навантажений узгоджено як по воду так і по виходу.

Література

1. Білицкий А.Ф. Лінійні пристрої апаратури зв’язку, Л.ВАЗ, 1973р. с.70-78.

2. Качанов Н.С. ЛРТУ, М.Воениздат, с.311-325.